Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T16:53:02.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffeomorphisms with infinitely many irrational invariant curves

Published online by Cambridge University Press:  23 November 2010

LEONARDO MORA  and
BLADISMIR RUIZ
LEONARDO MORA
Affiliation:
Departamento de Matemática, Facultad de Ciencias, La Hechicera, Universidad de los Andes, Mérida, 5101, Venezuela (email: [email protected], [email protected])
BLADISMIR RUIZ
Affiliation:
Departamento de Matemática, Facultad de Ciencias, La Hechicera, Universidad de los Andes, Mérida, 5101, Venezuela (email: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For a surface diffeomorphism f∈Diff l(M), with l≥8, we prove that if f exhibits a non-transversal heteroclinic cycle composed of two fixed saddle points Q1 and Q2, one dissipative and the other expansive, then there exists an open set 𝒱⊂Diff l(M) such that 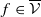and there exists a dense set 𝒟⊂𝒱 such that for all g∈𝒟, g exhibits infinitely many invariant periodic curves with irrational rotation numbers. Moreover, these curves are C1 conjugated to an irrational rotation on 𝕊1.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 31 , Issue 5 , October 2011 , pp. 1517 - 1535
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[Col98]Colli, E.. Infinitely many coexisting strange attractors. Ann. Inst. H. Poincaré Anal. Non Linéaire 15 (1998), 539–579.CrossRefGoogle Scholar
[GSS05]Gonchenko, S. V., Shilnikov, L. P. and Stenkin, O. V.. On Newhouse regions with infinitely many stable and unstable invariant tori. Progress in Nonlinear Science, Vol. 1. RAS, Institute of Applied Physics, Nizhniy Novgorod, 2002, pp. 80–102.Google Scholar
[GST07]Gonchenko, S. V., Shilnikov, L. P. and Turaev, D. V.. Homoclinic tangencies of arbitrarily high orders in conservative and dissipative two-dimensional maps. Nonlinearity 20(2) (2007), 241–275.CrossRefGoogle Scholar
[H76]Herman, M.. Mesure de Lebesgue et nombre de rotation (French). Geometry and Topology, Proc. III Latin Amer. School of Math., Inst. Mat. Pura Aplicada CNPq, Rio de Janeiro, 1976 (Lecture Notes in Mathematics, 597). Springer, Berlin, 1977, pp. 271–293.Google Scholar
[H79]Herman, M.. Sur la conjugaison differentielle des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49 (1979), 5–234.CrossRefGoogle Scholar
[I79]Ioos, G.. Bifurcation of Maps and Applications (North-Holland Mathematics Studies, 36). North-Holland Publishing Co., Amsterdam, 1979.Google Scholar
[N79]Newhouse, S.. The abundance of wild hyperbolic sets and nonsmooth stable sets for diffeomorphisms. Publ. Math. Inst. Hautes. Études. Sci. 50 (1979), 101–151.CrossRefGoogle Scholar
[PT93]Palis, J. and Takens, F.. Hyperbolicity and Sensitive Chaotic Dynamics at Homoclinic Bifurcations. Cambridge University Press, Cambridge, 1993.Google Scholar
[R89]Ruelle, D.. Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press, Boston, 1989.Google Scholar