Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T19:27:55.905Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffeomorphism cocycles over partially hyperbolic systems

Part of: Smooth dynamical systems: general theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  28 December 2020

VICTORIA SADOVSKAYA
VICTORIA SADOVSKAYA*
Affiliation:
Department of Mathematics, The Pennsylvania State University, University Park, PA16802, USA
*
e-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider Hölder continuous cocycles over an accessible partially hyperbolic system with values in the group of diffeomorphisms of a compact manifold $\mathcal {M}$ . We obtain several results for this setting. If a cocycle is bounded in 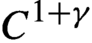$C^{1+\gamma }$ , we show that it has a continuous invariant family of 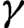$\gamma $ -Hölder Riemannian metrics on $\mathcal {M}$ . We establish continuity of a measurable conjugacy between two cocycles assuming bunching or existence of holonomies for both and pre-compactness in 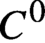$C^0$ for one of them. We give conditions for existence of a continuous conjugacy between two cocycles in terms of their cycle weights. We also study the relation between the conjugacy and holonomies of the cocycles. Our results give arbitrarily small loss of regularity of the conjugacy along the fiber compared to that of the holonomies and of the cocycle.

Keywords

Cocyclediffeomorphism grouppartially hyperbolic systemconjugacyisometry

MSC classification

Primary: 37D30: Partially hyperbolic systems and dominated splittings
Secondary: 37C15: Topological and differentiable equivalence, conjugacy, invariants, moduli, classification
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 1 , January 2022 , pp. 263 - 286
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Avila, A., Kocsard, A. and Liu, X.. Livšic theorem for diffeomorphism cocycles. Geom. Funct. Anal. 28 (2018), 943–964.CrossRefGoogle Scholar
Avila, A., Santamaria, J. and Viana, M.. Holonomy invariance: rough regularity and applications to Lyapunov exponents. Asterisque 358 (2013), 13–74.Google Scholar
Backes, L. and Kocsard, A.. Cohomology of dominated diffeomorphism-valued cocycles over hyperbolic systems. Ergod. Th. & Dynam. Sys. 36 (2015), 1703–1722.CrossRefGoogle Scholar
Burns, K. and Wilkinson, A.. On the ergodicity of partially hyperbolic systems. Ann. of Math. 171 (2010), 451–489.CrossRefGoogle Scholar
de la Llave, R.. Smooth conjugacy and SRB measures for uniformly and nonuniformly hyperbolic systems. Comm. Math. Phys. 150 (1992), 289–320.CrossRefGoogle Scholar
de la Llave, R. and Obaya, R.. Regularity of the composition operator in spaces of Hölder functions. Discrete Contin. Dyn. Syst. 5(1) (1999), 157–184.CrossRefGoogle Scholar
de la Llave, R. and Windsor, A.. Livšic theorem for non-commutative groups including groups of diffeomorphisms, and invariant geometric structures. Ergod. Th. & Dynam. Sys. 30(4) (2010), 1055–1100.CrossRefGoogle Scholar
de la Llave, R. and Windsor, A.. Smooth dependence on parameters of solutions to cohomology equations over Anosov systems with applications to cohomology equations on diffeomorphism groups. Discrete Contin. Dyn. Syst. 29(3) (2011), 1141–1154.CrossRefGoogle Scholar
Damjanovic, D. and Xu, D.. Diffeomorphism group valued cocycles over higher rank abelian Anosov actions. Ergod. Th. & Dynam. Sys. (2020), 40, 117–141.CrossRefGoogle Scholar
Kalinin, B. and Sadovskaya, V.. Holonomies and cohomology for cocyces over partially hyperbolic diffeomorphisms. Discrete Contin. Dyn. Syst. 36(1) (2016), 245–259.CrossRefGoogle Scholar
Kocsard, A. and Potrie, R.. Livšic theorem for low-dimensional diffeomorphism cocycles. Comment. Math. Helv. 91 (2016), 39–64.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54). Cambridge University Press, New York, 1995.CrossRefGoogle Scholar
Katok, A. and Nitica, V.. Rigidity of higher rank abelian cocycles with values in diffeomorphism groups. Geom. Dedicata 124 (2007), 109–131.CrossRefGoogle Scholar
Lang, S.. Fundamentals of Differential Geometry. Springer, New York, NY, 1999.CrossRefGoogle Scholar
Livšic, A. N.. Homology properties of Y-systems. Mat. Zametki 10 (1971), 758–763.Google Scholar
Livšic, A. N.. Cohomology of dynamical systems. Math. USSR Izv. 6 (1972), 1278–1301.CrossRefGoogle Scholar
Nitica, V. and Török, A.. Cohomology of dynamical systems and rigidity of partially hyperbolic actions of higher-rank lattices. Duke Math. J. 79(3) (1995), 751–810.CrossRefGoogle Scholar
Nitica, V. and Török, A.. Regularity results for the solutions of the Livsic cohomology equation with values in diffeomorphism groups. Ergod. Th. & Dynam. Sys. 16(2) (1996), 325–333.CrossRefGoogle Scholar
Nitica, V. and Török, A.. Regularity of the transfer map for cohomologous cocycles. Ergod. Th. & Dynam. Sys. 18(5) (1998), 1187–1209.CrossRefGoogle Scholar
Pollicott, M. and Walkden, C. P.. Livšic theorems for connected Lie groups. Trans. Amer. Math. Soc. 353(7) (2001), 2879–2895.CrossRefGoogle Scholar
Sadovskaya, V.. Boundedness and invariant metrics for diffeomorphism cocycles over hyperbolic systems. Geom. Dedicata 202(1) (2019), 401–417.CrossRefGoogle Scholar
Wilkinson, A.. The cohomological equation for partially hyperbolic diffeomorphisms. Astérisque 358 (2013), 75–165.Google Scholar