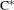Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-16T16:13:57.320Z Has data issue: false hasContentIssue false
  • English
  • Français

A dichotomy for groupoid $\text{C}^{\ast }$-algebras

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  13 August 2018

TIMOTHY RAINONE  and
AIDAN SIMS
TIMOTHY RAINONE
Affiliation:
School of Mathematics and Statistics, Arizona State University, Tempe, AZ 85287, USA email [email protected]
AIDAN SIMS
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, NSW 2522, Australia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the finite versus infinite nature of C$^{\ast }$-algebras arising from étale groupoids. For an ample groupoid 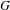$G$, we relate infiniteness of the reduced C$^{\ast }$-algebra 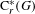$\text{C}_{r}^{\ast }(G)$ to notions of paradoxicality of a K-theoretic flavor. We construct a pre-ordered abelian monoid 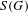$S(G)$ which generalizes the type semigroup introduced by Rørdam and Sierakowski for totally disconnected discrete transformation groups. 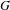This monoid characterizes the finite/infinite nature of the reduced groupoid C$^{\ast }$-algebra of $G$ in the sense that if 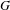$G$ is ample, minimal, topologically principal, and $S(G)$ is almost unperforated, we obtain a dichotomy between the stably finite and the purely infinite for 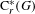$\text{C}_{r}^{\ast }(G)$. A type semigroup for totally disconnected topological graphs is also introduced, and we prove a similar dichotomy for these graph 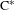$\text{C}^{\ast }$-algebras as well.

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 2 , February 2020 , pp. 521 - 563
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman-Delaroche, C.. Purely infinite C∗ -algebras arising from dynamical systems. Bull. Soc. Math. France 125 (1997), 199–225.Google Scholar
Anantharaman-Delaroche, C.. C∗ -algèbres de Cuntz-Krieger et groupes Fuchsiens (Operator Theory, Operator Algebras and Related Topics (Timisoara 1996)) . The Theta Foundation, Bucharest, 1997, pp. 17–35.Google Scholar
Ara, P., Moreno, M. A. and Pardo, E.. Non-stable K-theory for graph algebras. Algebr. Represent. Theory 10(2) (2007), 157–178.Google Scholar
Blackadar, B. and Rørdam, M.. Extending states on preordered semigroups and the existence of quasitraces on C∗ -algebras. J. Algebra 152 (1992), 240–247.Google Scholar
Bönicke, C. and Li, K.. Ideal structure and pure infiniteness of ample groupoid C∗ -algebras. Ergod. Th. & Dynam. Sys. (2018), doi:10.1017/etds.2018.39. Published online: 14 June 2018.Google Scholar
Brown, J., Clark, L. O., Farthing, C. and Sims, A.. Simplicity of algebras associated to étale groupoids. Semigroup Forum 88 (2014), 433–452.Google Scholar
Brown, J., Clark, L. and Sierakowski, A.. Purely infinite C∗ -algebras associated to étale groupoids. Ergod. Th. & Dynam. Sys. 35 (2015), 2397–2411.Google Scholar
Brown, L. G., Green, P. and Rieffel, M. A.. Stable isomorphism and strong Morita equivalence of C∗ -algebras. Pacific J. Math. 71 (1977), 349–363.Google Scholar
Brown, N.. AF embeddability of crossed products of AF algebras by the integers. J. Funct. Anal. 160 (1998), 150–175.Google Scholar
Carlsen, T. M., Ruiz, E. and Sims, A.. Equivalence and stable isomorphism of groupoids, and diagonal-preserving stable isomorphisms of graph C∗ -algebras and Leavitt path algebras. Proc. Amer. Math. Soc. 145 (2017), 1581–1592.Google Scholar
Clark, L. O., an Huef, A. and Sims, A.. AF-embeddability of 2-graph algebras and quasidiagonality of k-graph algebras. J. Funct. Anal. 271 (2016), 958–991.Google Scholar
Connes, A.. Noncommutative Geometry. Academic Press, San Diego, CA, 1994.Google Scholar
Cuntz, J.. K-theory for certain C∗ -algebras. Ann. of Math. (2) 113(1) (1981), 181–197.Google Scholar
Elliott, G., Gong, G., Lin, H. and Niu, Z.. On the classification of simple amenable C*-algebras with finite decomposition rank II. Preprint, 2015. arXiv:1507.03437 [math.OA].Google Scholar
Exel, R.. Reconstructing a totally disconnected groupoid from its ample semigroup. Proc. Amer. Math. Soc. 138 (2010), 2991–3001.Google Scholar
Folland, G. B.. Modern techniques and their applications. Real Analysis (Pure and Applied Mathematics (New York)) . Wiley-Interscience, New York, 1984.Google Scholar
Giordano, T., Putnam, I. F. and Skau, C. F.. Topological orbit equivalence and C∗ -crossed products. J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Gong, G., Lin, H. and Niu, Z.. Classification of simple amenable 𝓩-stable C ∗-algebras. Preprint, 2015. arXiv:1501.00135 [math.OA].Google Scholar
Haagerup, U.. Quasitraces on exact C∗ -algebras are traces. C. R. Math. Acad. Sci. Soc. R. Can. 36 (2014), 67–92.Google Scholar
Jolissaint, P. and Robertson, G.. Simple purely infinite C∗ -algebras and n-filling actions. J. Funct. Anal. 175 (2000), 197–213.Google Scholar
Katsura, T.. A class of C∗ -algebras generalizing both graph algebras and homeomorphism C∗ -algebras I, fundamental results. Trans. Amer. Math. Soc. 356 (2004), 4287–4322 (electronic).Google Scholar
Kishimoto, A. and Kumjian, A.. Crossed products of Cuntz algebras by quasi-free automorphisms. Operator Algebras and Their Applications (Waterloo, ON, 1994/1995) (Fields Institute Communications, 13) . American Mathematical Society, Providence, RI, 1997, pp. 173–192.Google Scholar
Kerr, D. and Nowak, P. W.. Residually finite actions and crossed products. Ergod. Th. & Dynam. Sys. 32 (2012), 1585–1614.Google Scholar
Kirchberg, E.. The Classification of Purely Infinite C∗ -Algebras Using Kasparaov’s Theory (Fields Institute Communication Series) . American Mathematical Society, Providence, RI, to appear.Google Scholar
Kirchberg, E. and Rørdam, M.. Non-simple purely infinite C∗ -algebras. Amer. J. Math. 122(3) (2000), 637–666.Google Scholar
Kirchberg, E. and Rørdam, M.. Infinite non-simple C∗ -algebras: absorbing the Cuntz Algebra 𝓞∞ . Adv. Math. 167 (2002), 195–264.Google Scholar
Kumjian, A. and Pask, D.. Higher rank graph C∗ -algebras. New York J. Math. 6 (2000), 1–20.Google Scholar
Laca, M. and Spielberg, J.. Purely infinite C∗ -algebras from boundary actions of discrete groups. J. Reine Angew. Math. 480 (1996), 125–139.Google Scholar
Li, H.. Purely infinite totally disconnected topological graph algebras. Illinois J. Math. 60(3–4) (2016), 739–750.Google Scholar
Li, X.. Continuous orbit equivalence rigidity. Ergod. Th. & Dynam. Sys. 38 (2018), 1543–1563.Google Scholar
Pask, D., Sierakowski, A. and Sims, A.. Unbounded quasitraces, stable finiteness and pure infiniteness. Preprint, 2017. arXiv:1705.01268 [math.OA].Google Scholar
Paterson, A.. Groupoids, Inverse Semigroups, and their Operator Algebras (Progress in Mathematics, 170) . Birkhauser, Boston, 1998.Google Scholar
Phillips, N. C.. A classification theorem for nuclear purely infinite simple C∗ -algebras. Doc. Math. 5 (2000), 49–114.Google Scholar
Pimsner, M.. Embedding some transformation group C∗ -algebras into AF-algebras. Ergod. Th. & Dynam. Sys. 3 (1983), 613–626.Google Scholar
Rainone, T.. MF actions and K-theoretic dynamics. J. Funct. Anal. 267 (2014), 542–578.Google Scholar
Rainone, T.. Paradoxical decompositions in C∗ -dynamical systems. J. Noncommut. Geom. 11 (2017), 791–822.Google Scholar
Rainone, T.. Noncommutative topological dynamics. Proc. Lond. Math. Soc. (3) 112(5) (2016), 903–923.Google Scholar
Rainone, T. and Schafhauser, C.. Crossed products of nuclear C∗-algebras by free groups and their traces. Preprint, 2016. arXiv:1601.06090 [math.OA].Google Scholar
Renault, J.. A Groupoid Approach to C∗ -Algebras (Lecture Notes in Mathematics, 793) . Springer, Berlin, 1980.Google Scholar
Renault, J. N., Sims, A., Williams, D. P. and Yeend, T.. Uniqueness theorems for topological higher-rank graph C∗ -algebras. Proc. Amer. Math. Soc. 146 (2018), 669–684.Google Scholar
Rørdam, M.. A simple C∗ -algebra with a finite and infinite projection. Acta Math. 191(01) (2003), 109–142.Google Scholar
Rørdam, M.. Classification of nuclear, simple C∗ -algebras. Classifcation of Nuclear C∗ -algebras. Entropy in Operator Algebras (Encyclopaedia of Mathematical Sciences, 126) . Springer, Berlin, 2002, pp. 1–145.Google Scholar
Rørdam, M. and Sierakowski, A.. Purely infinite C∗ -algebras arising from crossed products. Ergod. Th. & Dynam. Sys. 32 (2012), 273–293.Google Scholar
Spielberg, J.. Graph-based models for Kirchberg algebras. J. Operator Theory 57 (2007), 347–374.Google Scholar
Spielberg, J. S.. Free-product groups, Cuntz-Krieger algebras and covariant maps. Int. J. Math. 02(04) (1991), 457–476.Google Scholar
Suzuki, Y.. Construction of minimal skew products of amenable minimal dynamical systems. Groups Geom. Dyn. 11 (2017), 75–94.Google Scholar
Tikuisis, A., White, S. and Winter, W.. Quasidiagonality of nuclear C∗ -algebras. Ann. of Math. (2) 185 (2017), 229–284.Google Scholar
Wagon, S.. The Banach-Tarski Paradox. Cambridge University Press, Cambridge, 1993.Google Scholar
Winter, W.. On the classification of 𝓩-stable C∗ -algebras with real rank zero and finite decomposition rank. J. Lond. Math. Soc. (2) 179 (2006), 167–183.Google Scholar
Yeend, T.. Topological higher-rank graphs and the C∗ -algebras of topological 1-graphs. Operator Theory, Operator Algebras, and Applications (Contemporary Mathematics, 414) . American Mathematical Society, Providence, RI, 2006, pp. 231–244.Google Scholar