Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T01:16:45.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Destruction of invariant circles

Published online by Cambridge University Press:  10 December 2009

Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

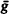Let in be an exact, area-preserving, monotone twist diffeomorphism of the cylinder and let 10 be a Liouville number. We will show that arbitrarily close to in the C∞ topology there exists a C∞ diffeomorphism with no homotopically non-trivial invariant circle of rotation number ω.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 8 , Volume 8: Charles Conley Memorial Issue , December 1988 , pp. 199 - 214
Copyright
Copyright © Cambridge University Press 1988

References

REFERENCES

Bangert, V.. Mather sets for twist maps and geodesics on tori. Dynam. Rep. To be published.Google Scholar
Birkhoff, G. D.. Sur quelques courbes fermées remarquables. Bull. Soc. Math. France 60 (1932), 1–26.Google Scholar
Reprinted in Collected Works, vol. II. New York (1950), 418–443.Google Scholar
Bullett, S.. Invariant circles for the piecewise linear standard map. Commun. Math. Phys. 107 (1986), 241–262.Google Scholar
Fathi, A.. Appendix to Ch. I of [5].Google Scholar
Herman, M.. Sur les courbes invariantes par les difféomorphismes de l'anneau, vol. 1. Astérisque 103–104 (1983).Google Scholar
Herman, M.. Sur les courbes invariantes par les difféomorphismes de l'anneau, vol. 2. Astérisque 144 (1986).Google Scholar
Mather, J.. Non-existence of invariant circles. Ergod. Th. & Dynam. Sys. 4 (1984), 301–309.10.1017/S0143385700002455Google Scholar
Mather, J.. A criterion for the non-existence of invariant circles. Publ. IHES 63 (1986), 153–204.10.1007/BF02831625Google Scholar
Mather, J.. More Denjoy minimal sets for area preserving diffeomorphisms. Comm. Math. Helv. 60 (1985), 508–557.10.1007/BF02567431Google Scholar
Mather, J.. Dynamics of area preserving mappings. Proc. ICM. To be published.Google Scholar
Mather, J.. Modulus of continuity for Peierls's barrier. Periodic Solutions of Hamiltonian Systems and Related Topics, ed. Rabinowitz, P. H. et al. NATO ASI Series C 209. D. Reidel, Dordrecht (1987), 177–202.10.1007/978-94-009-3933-2_18Google Scholar
Moser, J.. On invariant curves of area preserving mappings of an annulus. Nachr. Akad. Wiss. Göttingen, Math. Phys. Kl. (1962), 1–20.Google Scholar
Moser, J.. Stable and random motions in dynamical systems. Annals of Mathematical Studies 77. Princeton University Press (1973).Google Scholar
Salamon, D.. The Kolmogorov-Arnold-Moser theorem. Preprint. Forschungsinstitut für Mathematik, ETH Zürich (1986).Google Scholar
Robinson, C.. Generic properties of conservative systems. Amer. J. Math. 92 (1970), 562–603, 897–906.10.2307/2373361Google Scholar
Rudin, W.. Real and Complex Analysis. McGraw-Hill, New York (1966).Google Scholar