Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:01:33.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Density of half-horocycles on geometrically infinite hyperbolic surfaces

Published online by Cambridge University Press:  16 May 2012

BARBARA SCHAPIRA
BARBARA SCHAPIRA*
Affiliation:
LAMFA, UMR CNRS 6140, Université Picardie Jules Verne, 33 rue St Leu, 80000 Amiens, France (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

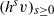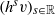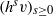On the unit tangent bundle of a hyperbolic surface, we study the density of positive orbits $(h^s v)_{s\ge 0}$ under the horocyclic flow. More precisely, given a full orbit $(h^sv)_{s\in {\mathbb R}}$, we prove that under a weak assumption on the vector $v$, both half-orbits $(h^sv)_{s\ge 0}$ and 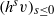$(h^s v)_{s\le 0}$ are simultaneously dense or not in the non-wandering set 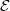$\mathcal {E}$of the horocyclic flow. We give also a counterexample to this result when this assumption is not satisfied.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 4 , August 2013 , pp. 1162 - 1177
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[C-D-P]Coornaert, M., Delzant, T. and Papadopoulos, A.. Géométrie et théorie des groupes. Les groupes hyperboliques de Gromov (Lecture Notes in Mathematics, 1441). Springer, Berlin, 1990.Google Scholar
[Da]Dal’bo, F.. Topologie du feuilletage fortement stable. Ann. Inst. Fourier (Grenoble) 50(3) (2000), 981–993.CrossRefGoogle Scholar
[E1]Eberlein, P.. Geodesic flows on negatively curved manifolds I. Ann. of Math. (2) 95 (1972), 492–510.Google Scholar
[G-Ha]Ghys, É. and de la Harpe, P.. Sur les groupes hyperboliques d’après Mikhael Gromov (Berne 1988) (Progress Mathematics, 83). Birkhäuser, 1990, pp. 1–25.Google Scholar
[H]Hedlund, G. A.. Fuchsian groups and transitive horocycles. Duke Math. J. 2 (1936), 530–542.Google Scholar
[Sa]Sarig, O.. The horocycle flow and the Laplacian on hyperbolic surfaces of infinite genus. Geom. Funct. Anal. 19(6) (2010), 1757–1812.CrossRefGoogle Scholar
[Scha]Schapira, B.. Density and equidistribution of half-horocycles on a geometrically finite hyperbolic surface. J. Lond. Math. Soc. 84(3) (2011), 785–806.CrossRefGoogle Scholar