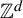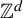1 Introduction
1.1 Decomposition of multicorrelation sequences
The structure and limiting behavior of (averages of) multicorrelation sequences, that is, sequences of the form
where
![]() $k\in \mathbb {N}, T_1,\ldots ,T_k\colon X\to X$
are invertible and commuting (that is,
$k\in \mathbb {N}, T_1,\ldots ,T_k\colon X\to X$
are invertible and commuting (that is,
![]() $T_iT_j=T_jT_i$
for all
$T_iT_j=T_jT_i$
for all
![]() $i,j$
) measure-preserving transformations on a probability space
$i,j$
) measure-preserving transformations on a probability space
![]() $(X,\mathcal {B},\mu )$
,
$(X,\mathcal {B},\mu )$
,
![]() $f_0,\ldots ,f_k\in L^\infty (\mu )$
and
$f_0,\ldots ,f_k\in L^\infty (\mu )$
and
![]() $n_1,\ldots ,n_k\in \mathbb {Z},$
is a central topic in ergodic theory. (We say that T preserves
$n_1,\ldots ,n_k\in \mathbb {Z},$
is a central topic in ergodic theory. (We say that T preserves
![]() $\mu $
if
$\mu $
if
![]() $\mu (T^{-1}A)=\mu (A)$
for all
$\mu (T^{-1}A)=\mu (A)$
for all
![]() $A\in \mathcal {B}.$
The tuple
$A\in \mathcal {B}.$
The tuple
![]() $(X,\mathcal {B},\mu ,T_1,\ldots ,T_k)$
is a (measure-preserving) system.) For
$(X,\mathcal {B},\mu ,T_1,\ldots ,T_k)$
is a (measure-preserving) system.) For
![]() $k=1$
, Herglotz–Bochner’s theorem implies that the sequence
$k=1$
, Herglotz–Bochner’s theorem implies that the sequence
![]() $\int _X f_0 \cdot T_1^nf_1 \, d\mu $
is given by the Fourier coefficients of some finite complex measure
$\int _X f_0 \cdot T_1^nf_1 \, d\mu $
is given by the Fourier coefficients of some finite complex measure
![]() $\sigma $
on
$\sigma $
on
![]() ${\mathbb T}$
(see [Reference Khintchine22, Reference Koopman and von Neumann23]). More specifically, decomposing
${\mathbb T}$
(see [Reference Khintchine22, Reference Koopman and von Neumann23]). More specifically, decomposing
![]() $\sigma $
into the sum of its atomic part,
$\sigma $
into the sum of its atomic part,
![]() $\sigma _a$
, and continuous part,
$\sigma _a$
, and continuous part,
![]() $\sigma _c$
, we get
$\sigma _c$
, we get
where
![]() $(\psi (n))$
is an almost periodic sequence (that is, there exists a compact abelian group G, a continuous function
$(\psi (n))$
is an almost periodic sequence (that is, there exists a compact abelian group G, a continuous function
![]() $\phi : G \rightarrow {\mathbb C}$
, and
$\phi : G \rightarrow {\mathbb C}$
, and
![]() $a \in G$
such that
$a \in G$
such that
![]() $\psi (n)=\phi (a^n), n\in \mathbb {N}$
) and
$\psi (n)=\phi (a^n), n\in \mathbb {N}$
) and
![]() $(\nu (n))$
is a nullsequence, that is,
$(\nu (n))$
is a nullsequence, that is,
 $$ \begin{align} \lim_{N-M \to \infty} \frac{1}{N-M} \sum_{n=M}^{N-1} |\nu(n)|^2=0. \end{align} $$
$$ \begin{align} \lim_{N-M \to \infty} \frac{1}{N-M} \sum_{n=M}^{N-1} |\nu(n)|^2=0. \end{align} $$
More generally, after Furstenberg’s celebrated ergodic theoretic proof of Szemerédi’s theorem [Reference Furstenberg15], for a single transformation T and iterates of the form
![]() $in, 1\leq i\leq k,$
there has been a particular interest in the study of the corresponding multicorrelation sequences
$in, 1\leq i\leq k,$
there has been a particular interest in the study of the corresponding multicorrelation sequences
For T ergodic (that is, every T-invariant set in
![]() $\mathcal {B}$
has trivial measure in
$\mathcal {B}$
has trivial measure in
![]() $\{0,1\}$
), Bergelson, Host, and Kra [Reference Bergelson, Host and Kra3] showed that the sequence
$\{0,1\}$
), Bergelson, Host, and Kra [Reference Bergelson, Host and Kra3] showed that the sequence
![]() $(\alpha (n))$
in equation (2) admits a decomposition of the form
$(\alpha (n))$
in equation (2) admits a decomposition of the form
![]() $a(n)=\phi (n)+\nu (n),$
where
$a(n)=\phi (n)+\nu (n),$
where
![]() $(\phi (n))$
is a uniform limit of k-step nilsequences (see §3.1 for the definition) and
$(\phi (n))$
is a uniform limit of k-step nilsequences (see §3.1 for the definition) and
![]() $(\nu (n))$
satisfies equation (1). (Note that k is the number of linear iterates that appear in equation (2).) Leibman, in [Reference Leibman28] for ergodic systems and [Reference Leibman29] for general ones, extended the result of Bergelson, Host, and Kra to polynomial iterates, meaning that in equation (2), instead of
$(\nu (n))$
satisfies equation (1). (Note that k is the number of linear iterates that appear in equation (2).) Leibman, in [Reference Leibman28] for ergodic systems and [Reference Leibman29] for general ones, extended the result of Bergelson, Host, and Kra to polynomial iterates, meaning that in equation (2), instead of
![]() $n,\ldots , kn,$
we have
$n,\ldots , kn,$
we have
![]() $p_1(n),\ldots ,p_k(n),$
for some
$p_1(n),\ldots ,p_k(n),$
for some
![]() $p_1,\ldots ,p_k\in \mathbb {Z}[x].$
$p_1,\ldots ,p_k\in \mathbb {Z}[x].$
For
![]() $d\in {\mathbb N}$
, we say that a tuple
$d\in {\mathbb N}$
, we say that a tuple
![]() $(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^d})$
is a
$(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^d})$
is a
![]() ${\mathbb Z}^d$
-measure-preserving system (or a
${\mathbb Z}^d$
-measure-preserving system (or a
![]() ${\mathbb Z}^d$
-system) if
${\mathbb Z}^d$
-system) if
![]() $(X,\mathcal {B},\mu )$
is a probability space and
$(X,\mathcal {B},\mu )$
is a probability space and
![]() $T_{n}\colon X\to X, n \in {\mathbb Z}^d,$
are measure-preserving transformations on X such that
$T_{n}\colon X\to X, n \in {\mathbb Z}^d,$
are measure-preserving transformations on X such that
![]() $T_{(0,\ldots ,0)}=\mathrm {id}$
and
$T_{(0,\ldots ,0)}=\mathrm {id}$
and
![]() $T_{m}\circ T_{n}=T_{m+n}$
for all
$T_{m}\circ T_{n}=T_{m+n}$
for all
![]() $m,n\in {\mathbb Z}^{d}$
. Notice here that we use the notation
$m,n\in {\mathbb Z}^{d}$
. Notice here that we use the notation
![]() $T_n$
to stress the fact that T is a
$T_n$
to stress the fact that T is a
![]() $\mathbb {Z}^d$
-action. If T is generated by the
$\mathbb {Z}^d$
-action. If T is generated by the
![]() $\mathbb {Z}$
-actions
$\mathbb {Z}$
-actions
![]() $T_1,\ldots ,T_d$
and
$T_1,\ldots ,T_d$
and
![]() $p_i=(p_{i,1},\ldots ,p_{i,d}),$
we have
$p_i=(p_{i,1},\ldots ,p_{i,d}),$
we have
![]() $T_{p_i(n)}=\prod _{j=1}^d T_j^{p_{i,j}(n)}.$
It is natural to ask whether splitting results still hold for systems with commuting transformations.
$T_{p_i(n)}=\prod _{j=1}^d T_j^{p_{i,j}(n)}.$
It is natural to ask whether splitting results still hold for systems with commuting transformations.
Question 1.1. [Reference Koutsogiannis, Le, Moreira and Richter27, Question 2]
Let
![]() $(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^d})$
be a
$(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^d})$
be a
![]() ${\mathbb Z}^d$
-system,
${\mathbb Z}^d$
-system,
![]() $k\in {\mathbb N}$
,
$k\in {\mathbb N}$
,
![]() $p_{1},\ldots ,p_{k}\colon {\mathbb Z}\to {\mathbb Z}^{d}$
a family of polynomials, and
$p_{1},\ldots ,p_{k}\colon {\mathbb Z}\to {\mathbb Z}^{d}$
a family of polynomials, and
![]() $f_0,f_1,\ldots ,f_k \in L^{\infty }(\mu )$
. Under which conditions on the system can the multicorrelation sequence
$f_0,f_1,\ldots ,f_k \in L^{\infty }(\mu )$
. Under which conditions on the system can the multicorrelation sequence
be decomposed as the sum of a uniform limit of nilsequences and a nullsequence?
The extension of the aforementioned results from
![]() $\mathbb {Z}$
to
$\mathbb {Z}$
to
![]() $\mathbb {Z}^d$
-actions is, to this day, a challenging open problem. The main issue is that the proofs of the splitting theorems crucially depend on the theory of characteristic factors via the structure theory developed by Host and Kra [Reference Host and Kra18], a tool that is unavailable in the more general
$\mathbb {Z}^d$
-actions is, to this day, a challenging open problem. The main issue is that the proofs of the splitting theorems crucially depend on the theory of characteristic factors via the structure theory developed by Host and Kra [Reference Host and Kra18], a tool that is unavailable in the more general
![]() $\mathbb {Z}^d$
-setting. By this, we mean that while nilfactors for
$\mathbb {Z}^d$
-setting. By this, we mean that while nilfactors for
![]() $\mathbb {Z}^d$
-analogs of Host–Kra uniformity norms are available (this can be found, for example, in [Reference Griesmer16]), it is in general not possible to relate averages such as equation (3) to those uniformity norms in the way one does for
$\mathbb {Z}^d$
-analogs of Host–Kra uniformity norms are available (this can be found, for example, in [Reference Griesmer16]), it is in general not possible to relate averages such as equation (3) to those uniformity norms in the way one does for
![]() $d=1$
. As an aside, Frantzikinakis provided a partial answer to Question 1.1 (for
$d=1$
. As an aside, Frantzikinakis provided a partial answer to Question 1.1 (for
![]() $d=1$
) in [Reference Frantzikinakis and Host10] that avoided the use of characteristic factors. The answer was partial in the sense that the nullsequence part was allowed to have an
$d=1$
) in [Reference Frantzikinakis and Host10] that avoided the use of characteristic factors. The answer was partial in the sense that the nullsequence part was allowed to have an
![]() $\ell ^{2}({\mathbb Z})$
error term. A similar decomposition result for general d was proven by Frantzikinakis and Host in [Reference Frantzikinakis, Host and Kra12]. (The third author showed in [Reference Koutsogiannis25] the analog to this result for integer parts, or any combination of rounding functions, of real polynomial iterates. For a refinement of this result, with the average of the error term taken along primes, see [Reference Koutsogiannis, Le, Moreira and Richter27].) From the point of view of applications, it is useful to have such splitting results for studying weighted averages, in particular for multiple commuting transformations. (It is worth mentioning that the splitting of equation (2), where the average in the null term is taken along primes, was used by Tao and Teräväinen to show the logarithmic Chowla conjecture for products of odd factors [Reference Tao and Teräväinen32].)
$\ell ^{2}({\mathbb Z})$
error term. A similar decomposition result for general d was proven by Frantzikinakis and Host in [Reference Frantzikinakis, Host and Kra12]. (The third author showed in [Reference Koutsogiannis25] the analog to this result for integer parts, or any combination of rounding functions, of real polynomial iterates. For a refinement of this result, with the average of the error term taken along primes, see [Reference Koutsogiannis, Le, Moreira and Richter27].) From the point of view of applications, it is useful to have such splitting results for studying weighted averages, in particular for multiple commuting transformations. (It is worth mentioning that the splitting of equation (2), where the average in the null term is taken along primes, was used by Tao and Teräväinen to show the logarithmic Chowla conjecture for products of odd factors [Reference Tao and Teräväinen32].)
It was demonstrated in [Reference Donoso, Koutsogiannis and Sun7] that under finitely many ergodicity assumptions (that is, we only have to assume that some iterates, coming from a finite set, of T are ergodic), the characteristic factors (defined in §2.3) for the corresponding averages
 $$ \begin{align} \frac{1}{N}\sum_{n=1}^{N}T_{p_{1}(n)}f_1\cdots T_{p_{k}(n)}f_k \end{align} $$
$$ \begin{align} \frac{1}{N}\sum_{n=1}^{N}T_{p_{1}(n)}f_1\cdots T_{p_{k}(n)}f_k \end{align} $$
are, as in the case of
![]() ${\mathbb Z}$
-actions, rotations on nilmanifolds. (A similar result was obtained in [Reference Johnson20] under infinitely many ergodicity assumptions. Such multiple ergodic averages always have
${\mathbb Z}$
-actions, rotations on nilmanifolds. (A similar result was obtained in [Reference Johnson20] under infinitely many ergodicity assumptions. Such multiple ergodic averages always have
![]() $L^2$
-limits as
$L^2$
-limits as
![]() $N\to \infty $
[Reference Walsh34].) So, it is reasonable to expect that Question 1.1 holds after postulating finitely many ergodicity assumptions (this is an open problem even in the
$N\to \infty $
[Reference Walsh34].) So, it is reasonable to expect that Question 1.1 holds after postulating finitely many ergodicity assumptions (this is an open problem even in the
![]() $k=2$
case—see [Reference Frantzikinakis, Host and Kra12]).
$k=2$
case—see [Reference Frantzikinakis, Host and Kra12]).
A partial answer toward this direction was obtained in [Reference Ferré Moragues9] by the second author. Namely, [Reference Ferré Moragues9, Theorem 1.5] shows that for any system
![]() $(X,\mathcal {B},\mu , T_1,\ldots , T_k)$
with
$(X,\mathcal {B},\mu , T_1,\ldots , T_k)$
with
![]() $T_i$
and
$T_i$
and
![]() $T_iT_j^{-1}$
ergodic (for all i and
$T_iT_j^{-1}$
ergodic (for all i and
![]() $j \neq i$
) and
$j \neq i$
) and
![]() $f_0,\ldots ,f_k \in L^{\infty }(\mu )$
, the sequence
$f_0,\ldots ,f_k \in L^{\infty }(\mu )$
, the sequence
can be decomposed as a sum of a uniform limit of k-step nilsequences plus a nullsequence.
For more general expressions (as in equation (3)), exploiting results from [Reference Johnson20], it is also shown in [Reference Ferré Moragues9] that if we further assume ergodicity in all directions, that is,
![]() $T_1^{a_1}\cdots T_d^{a_d}$
is ergodic for all
$T_1^{a_1}\cdots T_d^{a_d}$
is ergodic for all
![]() $(a_1,\ldots ,a_d) \in {\mathbb Z}^d \setminus \{\mathbf {{0}}\}$
, then for any family of pairwise distinct polynomials
$(a_1,\ldots ,a_d) \in {\mathbb Z}^d \setminus \{\mathbf {{0}}\}$
, then for any family of pairwise distinct polynomials
![]() $p_1,\ldots ,p_k\colon {\mathbb Z} \rightarrow {\mathbb Z}^d$
, the sequence
$p_1,\ldots ,p_k\colon {\mathbb Z} \rightarrow {\mathbb Z}^d$
, the sequence
can be decomposed as a sum of a uniform limit of D-step nilsequences plus a nullsequence. (Here D depends on
![]() $k, d$
and the maximum degree of the
$k, d$
and the maximum degree of the
![]() $p_i$
terms. It also has a connection to the number of van der Corput operations we have to run in the induction (see Remark 5.14 for details).) The proof of this result makes essential use of a seminorm bound estimate obtained in [Reference Johnson20], where the (infinitely many) ergodicity assumptions are reflected (see [Reference Ferré Moragues9, Theorem 1.6]).
$p_i$
terms. It also has a connection to the number of van der Corput operations we have to run in the induction (see Remark 5.14 for details).) The proof of this result makes essential use of a seminorm bound estimate obtained in [Reference Johnson20], where the (infinitely many) ergodicity assumptions are reflected (see [Reference Ferré Moragues9, Theorem 1.6]).
In [Reference Donoso, Koutsogiannis and Sun7], the first, third, and fourth authors improved the seminorm bound estimates of [Reference Johnson20] by imposing only finitely many ergodic assumptions. Although the results in [Reference Donoso, Koutsogiannis and Sun7] are stronger than those in [Reference Johnson20], one cannot apply them directly to [Reference Ferré Moragues9] to improve the aforementioned results, due to the incompatibility of the methods between the two studies [Reference Donoso, Koutsogiannis and Sun7, Reference Ferré Moragues9] (see §2.3 for more details).
In this article, we extend results from [Reference Donoso, Koutsogiannis and Sun7] to obtain splitting theorems for multicorrelation sequences involving multiparameter polynomials, postulating ergodicity assumptions which are even weaker than those in [Reference Donoso, Koutsogiannis and Sun7] on the transformations that define the
![]() $\mathbb {Z}^d$
-action in equation (6); for example, we will see that the sequence
$\mathbb {Z}^d$
-action in equation (6); for example, we will see that the sequence
![]() $\int _X f_0 \cdot T_1^{n^2}T_{2}^{n} f_1 \cdot T_3^{n^2}T_{4}^{n} f_2 \, d\mu $
admits the desired splitting if we assume that
$\int _X f_0 \cdot T_1^{n^2}T_{2}^{n} f_1 \cdot T_3^{n^2}T_{4}^{n} f_2 \, d\mu $
admits the desired splitting if we assume that
![]() $T_1, T_3, T_1T_3^{-1}$
are ergodic.
$T_1, T_3, T_1T_3^{-1}$
are ergodic.
1.2 The joint ergodicity phenomenon
In his ergodic theoretic proof of Szemerédi’s theorem, Furstenberg [Reference Furstenberg15] studied the averages of the multicorrelation sequence in equation (2). In particular, a stepping stone in the proof is the special case when the transformation T is weakly mixing (that is,
![]() $T\times T$
is ergodic for
$T\times T$
is ergodic for
![]() $\mu \times \mu $
), in which he showed that the averages
$\mu \times \mu $
), in which he showed that the averages
 $$ \begin{align} \frac{1}{N}\sum_{n=1}^N T^nf_1\cdots T^{kn}f_k \end{align} $$
$$ \begin{align} \frac{1}{N}\sum_{n=1}^N T^nf_1\cdots T^{kn}f_k \end{align} $$
converge in
![]() $L^2(\mu )$
to
$L^2(\mu )$
to
![]() $\prod _{i=1}^k \int _X f_i \, d\mu $
(which we will refer to as the ‘expected limit’) as
$\prod _{i=1}^k \int _X f_i \, d\mu $
(which we will refer to as the ‘expected limit’) as
![]() $N\to \infty $
. (Throughout this paper, unless otherwise stated, all limits of measurable functions on a measure-preserving system are taken in
$N\to \infty $
. (Throughout this paper, unless otherwise stated, all limits of measurable functions on a measure-preserving system are taken in
![]() $L^{2}$
.) It was Berend and Bergelson [Reference Berend and Bergelson1] who characterized when the average of the integrand of equation (5), that is, for multiple commuting transformations, converges to the expected limit (and this happens exactly when
$L^{2}$
.) It was Berend and Bergelson [Reference Berend and Bergelson1] who characterized when the average of the integrand of equation (5), that is, for multiple commuting transformations, converges to the expected limit (and this happens exactly when
![]() $T_1 \times \cdots \times T_k$
and
$T_1 \times \cdots \times T_k$
and
![]() $T_iT_j^{-1}$
for all
$T_iT_j^{-1}$
for all
![]() $i\neq j$
are ergodic).
$i\neq j$
are ergodic).
Generalizing Furstenberg’s result, Bergelson showed (in [Reference Bergelson2]) that, for a weakly mixing transformation T and essentially distinct polynomials
![]() $p_{1},\ldots ,p_{k}$
(that is,
$p_{1},\ldots ,p_{k}$
(that is,
![]() $p_{i}, p_{i}-p_{j}$
are non-constant for all
$p_{i}, p_{i}-p_{j}$
are non-constant for all
![]() $1\leq i,j\leq k, i\neq j$
),
$1\leq i,j\leq k, i\neq j$
),
 $$ \begin{align*} \lim_{N \to \infty} \frac{1}{N}\sum_{n=1}^N T^{p_1(n)}f_1\cdots T^{p_k(n)}f_k=\prod_{i=1}^k \int_X f_i \, d\mu.\end{align*} $$
$$ \begin{align*} \lim_{N \to \infty} \frac{1}{N}\sum_{n=1}^N T^{p_1(n)}f_1\cdots T^{p_k(n)}f_k=\prod_{i=1}^k \int_X f_i \, d\mu.\end{align*} $$
(For T totally ergodic (that is,
![]() $T^n$
is ergodic for all
$T^n$
is ergodic for all
![]() $n\in \mathbb {N}$
) and
$n\in \mathbb {N}$
) and
![]() $p_1,\ldots ,p_k$
‘independent’ integer polynomials, it is proved in [Reference Frantzikinakis and Kra14] that we have the same conclusion. This fact remains true for an ergodic T and ‘strongly independent’ real-valued polynomials iterates,
$p_1,\ldots ,p_k$
‘independent’ integer polynomials, it is proved in [Reference Frantzikinakis and Kra14] that we have the same conclusion. This fact remains true for an ergodic T and ‘strongly independent’ real-valued polynomials iterates,
![]() $[p_1(n)],\ldots ,[p_k(n)]$
(
$[p_1(n)],\ldots ,[p_k(n)]$
(
![]() $[\cdot ]$
denotes the floor function), as well (see [Reference Karageorgos and Koutsogiannis21]). These last two results also follow by a recent work of Frantzikinakis, [Reference Frantzikinakis11], in which, for single
$[\cdot ]$
denotes the floor function), as well (see [Reference Karageorgos and Koutsogiannis21]). These last two results also follow by a recent work of Frantzikinakis, [Reference Frantzikinakis11], in which, for single
![]() $T,$
we have a plethora of joint ergodicity results for a number of classes of iterates (not just polynomial). Finally, for real variable polynomial iterates, one is referred to [Reference Koutsogiannis26].) One can think of this last result as a strong independence property of the sequences
$T,$
we have a plethora of joint ergodicity results for a number of classes of iterates (not just polynomial). Finally, for real variable polynomial iterates, one is referred to [Reference Koutsogiannis26].) One can think of this last result as a strong independence property of the sequences
![]() $(T^{p_{i}(n)})_{n\in \mathbb {Z}}, 1\leq i\leq k$
in the weakly mixing case. It is reasonable to expect, under additional assumptions on the system and/or the polynomial iterates, convergence, of the averages appearing in the previous relation, to the expected limit, which naturally leads to a general notion of joint ergodicity (a sequence of finite subsets
$(T^{p_{i}(n)})_{n\in \mathbb {Z}}, 1\leq i\leq k$
in the weakly mixing case. It is reasonable to expect, under additional assumptions on the system and/or the polynomial iterates, convergence, of the averages appearing in the previous relation, to the expected limit, which naturally leads to a general notion of joint ergodicity (a sequence of finite subsets
![]() $(I_{N})_{N\in \mathbb {N}}$
of
$(I_{N})_{N\in \mathbb {N}}$
of
![]() $\mathbb {Z}^L$
with the property
$\mathbb {Z}^L$
with the property
![]() $\lim _{N\to \infty }\vert I_{N}\vert ^{-1}\cdot \vert (g+I_{N})\triangle I_{N}\vert =0$
for all
$\lim _{N\to \infty }\vert I_{N}\vert ^{-1}\cdot \vert (g+I_{N})\triangle I_{N}\vert =0$
for all
![]() $g\in \mathbb {Z}^L$
is called a Følner sequence in
$g\in \mathbb {Z}^L$
is called a Følner sequence in
![]() $\mathbb {Z}^L$
).
$\mathbb {Z}^L$
).
Definition 1.2. Let
![]() $d, k, L\in \mathbb {N}, p_1,\ldots ,p_k\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be polynomials and
$d, k, L\in \mathbb {N}, p_1,\ldots ,p_k\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be polynomials and
![]() $(X,\mathcal {B},\mu , (T_{g})_{g\in {\mathbb Z}^{d}})$
be a
$(X,\mathcal {B},\mu , (T_{g})_{g\in {\mathbb Z}^{d}})$
be a
![]() ${\mathbb Z}^{d}$
-system. We say that the sequence of tuples
${\mathbb Z}^{d}$
-system. We say that the sequence of tuples
![]() $(T_{p_{1}(n)},\ldots ,T_{p_{k}(n)})_{n\in \mathbb {Z}^{L}}$
is jointly ergodic for
$(T_{p_{1}(n)},\ldots ,T_{p_{k}(n)})_{n\in \mathbb {Z}^{L}}$
is jointly ergodic for
![]() $\mu $
if for every
$\mu $
if for every
![]() $f_{1},\ldots ,f_{k} \in L^{\infty }(\mu )$
and every Følner sequence
$f_{1},\ldots ,f_{k} \in L^{\infty }(\mu )$
and every Følner sequence
![]() $(I_{N})_{N\in \mathbb {N}}$
of
$(I_{N})_{N\in \mathbb {N}}$
of
![]() $\mathbb {Z}^{L}$
, we have that
$\mathbb {Z}^{L}$
, we have that
 $$ \begin{align} \lim_{N\to\infty}\frac{1}{\vert I_{N}\vert}\sum_{n\in I_{N}}T_{p_{1}(n)}f_{1}\cdots T_{p_{k}(n)}f_{k}=\int_{X}f_{1}\,d\mu\cdots \int_{X}f_{k}\,d\mu. \end{align} $$
$$ \begin{align} \lim_{N\to\infty}\frac{1}{\vert I_{N}\vert}\sum_{n\in I_{N}}T_{p_{1}(n)}f_{1}\cdots T_{p_{k}(n)}f_{k}=\int_{X}f_{1}\,d\mu\cdots \int_{X}f_{k}\,d\mu. \end{align} $$
When
![]() $k=1$
, we also say that
$k=1$
, we also say that
![]() $(T_{p_{1}(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for
$(T_{p_{1}(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for
![]() $\mu .$
$\mu .$
The following conjecture was stated in [Reference Donoso, Koutsogiannis and Sun7].
Conjecture 1.3. [Reference Donoso, Koutsogiannis and Sun7, Conjecture 1.5]
Let
![]() $d,k,L\in \mathbb {N}, p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be polynomials and
$d,k,L\in \mathbb {N}, p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be polynomials and
![]() $(X,\mathcal {B},\mu , (T_{g})_{g\in {\mathbb Z}^{d}})$
be a
$(X,\mathcal {B},\mu , (T_{g})_{g\in {\mathbb Z}^{d}})$
be a
![]() ${\mathbb Z}^{d}$
-system. Then the following are equivalent.
${\mathbb Z}^{d}$
-system. Then the following are equivalent.
-
(C1)
 $(T_{p_{1}(n)},\ldots ,T_{p_{k}(n)})_{n\in \mathbb {Z}^{L}}$
is jointly ergodic for
$(T_{p_{1}(n)},\ldots ,T_{p_{k}(n)})_{n\in \mathbb {Z}^{L}}$
is jointly ergodic for
 $\mu $
.
$\mu $
. -
(C2) The following conditions are satisfied:
-
(i)
 $(T_{p_{i}(n)-p_{j}(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for
$(T_{p_{i}(n)-p_{j}(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for
 $\mu $
for all
$\mu $
for all
 $1\leq i,j\leq k, i\neq j$
; and
$1\leq i,j\leq k, i\neq j$
; and -
(ii)
 $(T_{p_{1}(n)}\times \cdots \times T_{p_{k}(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for the product measure
$(T_{p_{1}(n)}\times \cdots \times T_{p_{k}(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for the product measure
 $\mu ^{\otimes k}$
on
$\mu ^{\otimes k}$
on
 $X^{k}$
.
$X^{k}$
.
-
Answering a question of Bergelson, it was shown in [Reference Donoso, Koutsogiannis and Sun7, Theorem 1.4] that for a polynomial
![]() $p:\mathbb {Z}^L\to \mathbb {Z},$
the sequence
$p:\mathbb {Z}^L\to \mathbb {Z},$
the sequence
![]() $(T_{1}^{p(n)},\ldots ,T_{k}^{p(n)})_{n\in \mathbb {Z}^{L}}$
is jointly ergodic for
$(T_{1}^{p(n)},\ldots ,T_{k}^{p(n)})_{n\in \mathbb {Z}^{L}}$
is jointly ergodic for
![]() $\mu $
if and only if
$\mu $
if and only if
![]() $((T_{1}\times \cdots \times T_{k})^{p(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for
$((T_{1}\times \cdots \times T_{k})^{p(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for
![]() $\mu ^{\otimes k}$
and
$\mu ^{\otimes k}$
and
![]() $T_{i}T^{-1}_{j}$
is ergodic for
$T_{i}T^{-1}_{j}$
is ergodic for
![]() $\mu $
for all
$\mu $
for all
![]() $i\neq j.$
In this paper, the strong decomposition results that we obtain allow us to deduce joint ergodicity results for a larger family of polynomials (see Theorems 2.5 and 2.9), thus addressing some additional cases in the aforementioned conjecture.
$i\neq j.$
In this paper, the strong decomposition results that we obtain allow us to deduce joint ergodicity results for a larger family of polynomials (see Theorems 2.5 and 2.9), thus addressing some additional cases in the aforementioned conjecture.
2 Main results
In this section, we state the main results of the paper and provide a number of examples to better illustrate them. We also comment on the approaches that we follow.
2.1 Splitting results
Our first main concern is to resolve the incompatibility between [Reference Donoso, Koutsogiannis and Sun7] and [Reference Ferré Moragues9], and improve the method in [Reference Donoso, Koutsogiannis and Sun7], to obtain an extension of the results in [Reference Ferré Moragues9].
Before we state our first result, we need to introduce some notation.
For
![]() $d,L\in \mathbb {N}$
, the polynomial
$d,L\in \mathbb {N}$
, the polynomial
![]() $q=(q_1,\ldots ,q_d): \mathbb {Z}^L\to \mathbb {Z}^d$
is non-constant if some
$q=(q_1,\ldots ,q_d): \mathbb {Z}^L\to \mathbb {Z}^d$
is non-constant if some
![]() $q_i$
is non-constant. Here we mean that each
$q_i$
is non-constant. Here we mean that each
![]() $q_i$
is a member of
$q_i$
is a member of
![]() $\mathbb {Q}[x_1,\ldots ,x_L]$
with
$\mathbb {Q}[x_1,\ldots ,x_L]$
with
![]() ${q_i(\mathbb {Z}^L)\subseteq \mathbb {Z}.}$
The degree of q is defined as the maximum of the degrees of the
${q_i(\mathbb {Z}^L)\subseteq \mathbb {Z}.}$
The degree of q is defined as the maximum of the degrees of the
![]() $q_i$
terms.
$q_i$
terms.
The polynomials
![]() $p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
are called essentially distinct if they are non-constant and
$p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
are called essentially distinct if they are non-constant and
![]() $p_{i}-p_{j}$
is non-constant for all
$p_{i}-p_{j}$
is non-constant for all
![]() $i\neq j$
. (In general, a polynomial
$i\neq j$
. (In general, a polynomial
![]() ${q\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}}$
has rational coefficients (that is, vectors with rational coordinates).)
${q\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}}$
has rational coefficients (that is, vectors with rational coordinates).)
For a subset A of
![]() $\mathbb {Q}^{d}$
, we denote
$\mathbb {Q}^{d}$
, we denote ![]() The following subgroups of
The following subgroups of
![]() ${\mathbb Z}^{d}$
play an important role in this paper.
${\mathbb Z}^{d}$
play an important role in this paper.
Definition 2.1. Let
![]() ${\mathbf {p}}=(p_{1},\ldots ,p_{k}), p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be a family of essentially distinct polynomials with
${\mathbf {p}}=(p_{1},\ldots ,p_{k}), p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be a family of essentially distinct polynomials with
![]() $p_{i}(n)=\sum _{v\in \mathbb {N}_0^{L}}b_{i,v}n^{v}$
for some
$p_{i}(n)=\sum _{v\in \mathbb {N}_0^{L}}b_{i,v}n^{v}$
for some
![]() $b_{i,v}\in \mathbb {Q}^{d}$
with at most finitely many
$b_{i,v}\in \mathbb {Q}^{d}$
with at most finitely many
![]() $b_{i,v},v\in \mathbb {N}_0^{L}$
non-zero. (Here, we denote
$b_{i,v},v\in \mathbb {N}_0^{L}$
non-zero. (Here, we denote ![]() for
for
![]() ${n=(n_{1},\ldots ,n_{L})\in {\mathbb Z}^{L}}$
and
${n=(n_{1},\ldots ,n_{L})\in {\mathbb Z}^{L}}$
and
![]() $v=(v_{1},\ldots ,v_{L})\in {\mathbb N}_0^{L}$
, where
$v=(v_{1},\ldots ,v_{L})\in {\mathbb N}_0^{L}$
, where
![]() $0^0:=1.$
) For convenience, we artificially denote
$0^0:=1.$
) For convenience, we artificially denote
![]() $p_{0}$
as the constant zero polynomial and
$p_{0}$
as the constant zero polynomial and ![]() for all
for all
![]() $v\in {\mathbb N}_{0}^{L}$
. For
$v\in {\mathbb N}_{0}^{L}$
. For
![]() $0\leq i,j\leq k$
, set
$0\leq i,j\leq k$
, set ![]() and
and ![]() , where, for
, where, for
![]() $v=(v_1,\ldots ,v_L)\in {\mathbb N}_{0}^{L},$
we write
$v=(v_1,\ldots ,v_L)\in {\mathbb N}_{0}^{L},$
we write
![]() $\vert v\vert =v_1+\cdots +v_L.$
$\vert v\vert =v_1+\cdots +v_L.$
Our main result provides an affirmative answer to Question 1.1 under finitely many ergodicity assumptions on the groups
![]() $G_{i,j}(\mathbf {p})$
, which generalizes [Reference Ferré Moragues9, Theorem 1.5]. We say that the group
$G_{i,j}(\mathbf {p})$
, which generalizes [Reference Ferré Moragues9, Theorem 1.5]. We say that the group
![]() $G_{i,j}(\mathbf {p})$
is ergodic for
$G_{i,j}(\mathbf {p})$
is ergodic for
![]() $\mu $
if any function
$\mu $
if any function
![]() $f \in L^2(\mu )$
that is
$f \in L^2(\mu )$
that is
![]() $T_{a}$
-invariant for all
$T_{a}$
-invariant for all
![]() $a \in G_{i,j}(\mathbf {p})$
is constant.
$a \in G_{i,j}(\mathbf {p})$
is constant.
The definition of a D-step nilsequence will be given in §3.1. We say that
![]() $a\colon {\mathbb Z}^L \to {\mathbb C}$
is a nullsequence if for any Følner sequence
$a\colon {\mathbb Z}^L \to {\mathbb C}$
is a nullsequence if for any Følner sequence
![]() $(I_N)_{N\in {\mathbb N}}, \lim _{N \to \infty } {1}/{|I_N|} \sum _{n \in I_N} |a(n)|^2=0.$
$(I_N)_{N\in {\mathbb N}}, \lim _{N \to \infty } {1}/{|I_N|} \sum _{n \in I_N} |a(n)|^2=0.$
Theorem 2.2. (Decomposition theorem under finitely many ergodicity assumptions)
For
![]() $d,k,K,L\in \mathbb {N},$
let
$d,k,K,L\in \mathbb {N},$
let
![]() $\mathbf {p}=(p_{1},\ldots ,p_{k}),$
where
$\mathbf {p}=(p_{1},\ldots ,p_{k}),$
where
![]() $p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
is a family of essentially distinct polynomials of degree at most
$p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
is a family of essentially distinct polynomials of degree at most
![]() $K,$
and let
$K,$
and let
![]() $(X,\mathcal {B},\mu , (T_{n})_{n\in {\mathbb Z}^{d}})$
be a
$(X,\mathcal {B},\mu , (T_{n})_{n\in {\mathbb Z}^{d}})$
be a
![]() ${\mathbb Z}^{d}$
-system. If
${\mathbb Z}^{d}$
-system. If
![]() $G_{i,j}(\mathbf {p})$
is ergodic for
$G_{i,j}(\mathbf {p})$
is ergodic for
![]() $\mu $
for all
$\mu $
for all
![]() $0\leq i,j\leq k,i\neq j,$
then for all
$0\leq i,j\leq k,i\neq j,$
then for all
![]() $f_0,\ldots ,f_k \in L^{\infty }(\mu )$
, the multicorrelation sequence
$f_0,\ldots ,f_k \in L^{\infty }(\mu )$
, the multicorrelation sequence
can be decomposed as a sum of a uniform limit of D-step nilsequences and a nullsequence, where
![]() $D\in {\mathbb N}$
is a constant depending only on
$D\in {\mathbb N}$
is a constant depending only on
![]() $d,k,K,L.$
$d,k,K,L.$
We refer the reader to Remark 5.14 for a further discussion on the constant D. Also, note that Theorem 2.2 goes beyond Question 1.1 as it deals with multivariable polynomial iterates (that is,
![]() $L>1$
).
$L>1$
).
Example 2.3. It was proved in [Reference Ferré Moragues9, Theorem 1.5] that for any probability space
![]() $(X,\mathcal {B},\mu )$
and commuting transformations
$(X,\mathcal {B},\mu )$
and commuting transformations
![]() $T_{1},\ldots ,T_{k}$
acting on X, if
$T_{1},\ldots ,T_{k}$
acting on X, if
![]() $T_i$
and
$T_i$
and
![]() $T_iT_j^{-1}$
are ergodic (for all i and all
$T_iT_j^{-1}$
are ergodic (for all i and all
![]() $j \neq i$
, respectively), then for all
$j \neq i$
, respectively), then for all
![]() $f_0,\ldots ,f_k \in L^{\infty }(\mu )$
, the multicorrelation sequence
$f_0,\ldots ,f_k \in L^{\infty }(\mu )$
, the multicorrelation sequence
can be decomposed as a sum of a uniform limit of k-step nilsequences plus a nullsequence. While Theorem 2.2 does not specify the step D of the nilsequence, a quick argument shows that, in this case, one can indeed take
![]() $D=k$
(see Remark 6.1 for details).
$D=k$
(see Remark 6.1 for details).
The following example shows that Theorem 2.2 is stronger than [Reference Ferré Moragues9, Theorem 1.6], which deals with single variable essentially distinct polynomial iterates.
Example 2.4. Let
![]() $(X,\mathcal {B},\mu ,T_{1},\ldots ,T_{6})$
be a system with commuting transformations
$(X,\mathcal {B},\mu ,T_{1},\ldots ,T_{6})$
be a system with commuting transformations
![]() $T_{1},\ldots ,T_{6}$
and
$T_{1},\ldots ,T_{6}$
and
![]() $f_{0},f_{1},\ldots ,f_{4}\in L^{\infty }(\mu )$
. Using [Reference Ferré Moragues9, Theorem 1.6], we have that the multicorrelation sequence
$f_{0},f_{1},\ldots ,f_{4}\in L^{\infty }(\mu )$
. Using [Reference Ferré Moragues9, Theorem 1.6], we have that the multicorrelation sequence
can be decomposed as the sum of a uniform limit of nilsequences and a nullsequence if
![]() $T^{a_{1}}_{1}\cdots T^{a_{6}}_{6}$
is ergodic for all
$T^{a_{1}}_{1}\cdots T^{a_{6}}_{6}$
is ergodic for all
![]() $(a_{1},\ldots ,a_{6})\in {\mathbb Z}^{6}\backslash \{\mathbf {{0}}\}$
. In contrast, via Theorem 2.2, one can get the same conclusion by only assuming that
$(a_{1},\ldots ,a_{6})\in {\mathbb Z}^{6}\backslash \{\mathbf {{0}}\}$
. In contrast, via Theorem 2.2, one can get the same conclusion by only assuming that
![]() $T_{1},T_{2}T_{3}^{-1}, T_{4},T_{5},T_{4}T^{-1}_{5}$
are ergodic. (Indeed, denoting
$T_{1},T_{2}T_{3}^{-1}, T_{4},T_{5},T_{4}T^{-1}_{5}$
are ergodic. (Indeed, denoting ![]() , and
, and
![]() $e_{i}$
the vector whose ith entry is 1 and all other entries are 0, since
$e_{i}$
the vector whose ith entry is 1 and all other entries are 0, since
![]() $\mathbf {{p}}=((n^2,n,0,0,0,0),(n^2,0,n,0,0,0)$
,
$\mathbf {{p}}=((n^2,n,0,0,0,0),(n^2,0,n,0,0,0)$
,
![]() $(0,0,0,n^3,0,0)$
,
$(0,0,0,n^3,0,0)$
,
![]() $(0,0,0,0,n^3,n)),$
we have that
$(0,0,0,0,n^3,n)),$
we have that
![]() $G_{1,0}(\mathbf {p})=G_{2,0}(\mathbf {p})=G(e_{1})$
,
$G_{1,0}(\mathbf {p})=G_{2,0}(\mathbf {p})=G(e_{1})$
,
![]() $G_{1,3}(\mathbf {p})= G_{2,3}(\mathbf {p})=G_{3,0}(\mathbf {p})\ =\ G(e_{4})$
,
$G_{1,3}(\mathbf {p})= G_{2,3}(\mathbf {p})=G_{3,0}(\mathbf {p})\ =\ G(e_{4})$
,
![]() $G_{1,4}(\mathbf {p})\ =\ G_{2,4}(\mathbf {p})\ =\ G_{4,0}(\mathbf {p})\ =\ G(e_{5})$
,
$G_{1,4}(\mathbf {p})\ =\ G_{2,4}(\mathbf {p})\ =\ G_{4,0}(\mathbf {p})\ =\ G(e_{5})$
,
![]() ${G_{1,2}(\mathbf {p})\ =\ G(e_{2}-e_{3})}$
,
${G_{1,2}(\mathbf {p})\ =\ G(e_{2}-e_{3})}$
,
![]() $G_{3,4}(\mathbf {p})=G(e_{4}-e_{5})$
.)
$G_{3,4}(\mathbf {p})=G(e_{4}-e_{5})$
.)
2.2 Convergence to the expected limit
In [Reference Donoso, Koutsogiannis and Sun7, Theorem 1.4], the first, third, and fourth authors proved the following case of Conjecture 1.3. If
![]() $T_{1},\ldots ,T_{k}$
are commuting transformations acting on a probability space
$T_{1},\ldots ,T_{k}$
are commuting transformations acting on a probability space
![]() $(X,\mathcal {B},\mu )$
, then
$(X,\mathcal {B},\mu )$
, then
![]() $(T_{1}^{p(n)},\ldots ,T_{k}^{p(n)})_{n\in \mathbb {Z}^{L}}$
is jointly ergodic for
$(T_{1}^{p(n)},\ldots ,T_{k}^{p(n)})_{n\in \mathbb {Z}^{L}}$
is jointly ergodic for
![]() $\mu $
if and only if
$\mu $
if and only if
![]() $((T_{1}\times \cdots \times T_{k})^{p(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for
$((T_{1}\times \cdots \times T_{k})^{p(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for
![]() $\mu ^{\otimes k}$
and
$\mu ^{\otimes k}$
and
![]() $T_{i}T^{-1}_{j}$
is ergodic for
$T_{i}T^{-1}_{j}$
is ergodic for
![]() $\mu $
for all
$\mu $
for all
![]() $i\neq j$
. In this paper, we further extend this result.
$i\neq j$
. In this paper, we further extend this result.
Theorem 2.5. Let
![]() $k,d,L\in {\mathbb N}$
and
$k,d,L\in {\mathbb N}$
and
![]() $\mathbf {p}=(p_{1}v_{1},\ldots , p_{k}v_{k}),$
where
$\mathbf {p}=(p_{1}v_{1},\ldots , p_{k}v_{k}),$
where
![]() $p_{1},\ldots , p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}$
,
$p_{1},\ldots , p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}$
,
![]() $v_{1},\ldots , v_{k}\in {\mathbb Z}^{d}$
be a family of essentially distinct polynomials. Suppose that for all
$v_{1},\ldots , v_{k}\in {\mathbb Z}^{d}$
be a family of essentially distinct polynomials. Suppose that for all
![]() $1\leq i,j\leq k$
, if
$1\leq i,j\leq k$
, if
![]() $\deg (p_{i})=\deg (p_{j})$
, then either
$\deg (p_{i})=\deg (p_{j})$
, then either
![]() $v_{i}$
and
$v_{i}$
and
![]() $v_{j}$
are linearly dependent over
$v_{j}$
are linearly dependent over
![]() $\mathbb {Z}$
, or
$\mathbb {Z}$
, or
![]() $p_{i}$
and
$p_{i}$
and
![]() $p_{j}$
are linearly dependent over
$p_{j}$
are linearly dependent over
![]() $\mathbb {Z}$
(that is, there is a non-trivial linear combination of them over
$\mathbb {Z}$
(that is, there is a non-trivial linear combination of them over
![]() $\mathbb {Z}$
which equals to a constant). Let
$\mathbb {Z}$
which equals to a constant). Let
![]() $(X,\mathcal {B},\mu , (T_{g})_{g\in \mathbb {Z}^{d}})$
be a
$(X,\mathcal {B},\mu , (T_{g})_{g\in \mathbb {Z}^{d}})$
be a
![]() $\mathbb {Z}^{d}$
-system. Then the following are equivalent.
$\mathbb {Z}^{d}$
-system. Then the following are equivalent.
-
(C1)
 $(T_{p_{1}(n)v_{1}},\ldots ,T_{p_{k}(n)v_{k}})_{n\in {\mathbb Z}^{L}}$
is jointly ergodic for
$(T_{p_{1}(n)v_{1}},\ldots ,T_{p_{k}(n)v_{k}})_{n\in {\mathbb Z}^{L}}$
is jointly ergodic for
 $\mu .$
$\mu .$
-
(C2’) The following subconditions hold:
-
(i)’
 $(T_{p_{i}(n)v_{i}-p_{j}(n)v_{j}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{p_{i}(n)v_{i}-p_{j}(n)v_{j}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
 $\mu $
for all
$\mu $
for all
 $1\leq i,j\leq k, i\neq j$
with
$1\leq i,j\leq k, i\neq j$
with
 $\deg (p_{i})=\deg (p_{j})$
;
$\deg (p_{i})=\deg (p_{j})$
; -
(ii)
 $(T_{p_{1}(n)v_{1}}\times \cdots \times T_{p_{k}(n)v_{k}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{p_{1}(n)v_{1}}\times \cdots \times T_{p_{k}(n)v_{k}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
 $\mu ^{\otimes k}$
.
$\mu ^{\otimes k}$
.
-
Moreover, condition (C2’) is equivalent to
-
(C2) The following subconditions hold:
-
(i)
 $(T_{p_{i}(n)v_{i}-p_{j}(n)v_{j}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{p_{i}(n)v_{i}-p_{j}(n)v_{j}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
 $\mu $
for all
$\mu $
for all
 $1\leq i,j\leq k, i\neq j$
;
$1\leq i,j\leq k, i\neq j$
; -
(ii)
 $(T_{p_{1}(n)v_{1}}\times \cdots \times T_{p_{k}(n)v_{k}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{p_{1}(n)v_{1}}\times \cdots \times T_{p_{k}(n)v_{k}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
 $\mu ^{\otimes k}$
.
$\mu ^{\otimes k}$
.
-
Note that the subconditions in condition (C2) are consistent with those in Conjecture 1.3. However, the reason we provide an alternative set of equivalent subconditions in condition (C2’) is that these subconditions are easier to check in practice.
We now give some examples to illustrate Theorem 2.5. The first one is for polynomials of distinct degrees.
Example 2.6. Let
![]() $(X,\mathcal {B},\mu ,T_{1},\ldots ,T_{k})$
be a system. Using Theorem 2.5, we conclude that
$(X,\mathcal {B},\mu ,T_{1},\ldots ,T_{k})$
be a system. Using Theorem 2.5, we conclude that
![]() $(T^{n}_{1},T^{n^{2}}_{2},\ldots ,T^{n^{k}}_{k})_{n\in {\mathbb Z}}$
is jointly ergodic if and only if
$(T^{n}_{1},T^{n^{2}}_{2},\ldots ,T^{n^{k}}_{k})_{n\in {\mathbb Z}}$
is jointly ergodic if and only if
![]() $(T^{n}_{1}\times \cdots \times T^{n^{k}}_{k})_{n\in {\mathbb Z}}$
is ergodic for
$(T^{n}_{1}\times \cdots \times T^{n^{k}}_{k})_{n\in {\mathbb Z}}$
is ergodic for
![]() $\mu ^{\otimes k}$
, and all the
$\mu ^{\otimes k}$
, and all the
![]() $T_{i}$
terms are ergodic for
$T_{i}$
terms are ergodic for
![]() $\mu $
.
$\mu $
.
We remark that Example 2.6 can also be proved by using arguments from [Reference Chu, Frantzikinakis and Host6]. We next present two examples in which some polynomials have the same degree and so cannot be recovered by the methods of [Reference Chu, Frantzikinakis and Host6].
Example 2.7. Let
![]() $(X,\mathcal {B},\mu ,T_{1},T_2,T_3,T_{4})$
be a system. Theorem 2.5 implies that
$(X,\mathcal {B},\mu ,T_{1},T_2,T_3,T_{4})$
be a system. Theorem 2.5 implies that
![]() $(T^{n}_{1},T^{n}_{2},T^{n^{2}}_{3}, T^{n^{2}}_{4})_{n\in {\mathbb Z}}$
is jointly ergodic if and only if
$(T^{n}_{1},T^{n}_{2},T^{n^{2}}_{3}, T^{n^{2}}_{4})_{n\in {\mathbb Z}}$
is jointly ergodic if and only if
![]() $(T^{n}_{1}\times T^{n}_{2}\times T^{n^{2}}_{3}\times T^{n^{2}}_{4})_{n\in {\mathbb Z}}$
is ergodic for
$(T^{n}_{1}\times T^{n}_{2}\times T^{n^{2}}_{3}\times T^{n^{2}}_{4})_{n\in {\mathbb Z}}$
is ergodic for
![]() $\mu ^{\otimes 4}$
, and both
$\mu ^{\otimes 4}$
, and both
![]() $T_{1}T^{-1}_{2}$
and
$T_{1}T^{-1}_{2}$
and
![]() $((T_{3}T^{-1}_{4})^{n^2})_{n\in {\mathbb N}}$
are ergodic for
$((T_{3}T^{-1}_{4})^{n^2})_{n\in {\mathbb N}}$
are ergodic for
![]() $\mu $
.
$\mu $
.
Example 2.8. Let
![]() $(X,\mathcal {B},\mu ,T_{1},T_2,T_3)$
be a system. Theorem 2.5 implies that
$(X,\mathcal {B},\mu ,T_{1},T_2,T_3)$
be a system. Theorem 2.5 implies that
![]() $(T^{n^{4}+n^{2}}_{1}$
,
$(T^{n^{4}+n^{2}}_{1}$
,
![]() $T^{2n^{4}+3n}_{1}, T^{2n^{2}+2n+1}_{2}, T^{3n^{2}+3n}_{3})_{n\in {\mathbb Z}}$
is jointly ergodic if and only if
$T^{2n^{4}+3n}_{1}, T^{2n^{2}+2n+1}_{2}, T^{3n^{2}+3n}_{3})_{n\in {\mathbb Z}}$
is jointly ergodic if and only if
![]() $(T^{n^{4}+n^{2}}_{1}\times T^{2n^{4}+3n}_{1}\times T^{2n^{2}+2n+1}_{2}\times T^{3n^{2}+3n}_{3})_{n\in {\mathbb Z}}$
is ergodic for
$(T^{n^{4}+n^{2}}_{1}\times T^{2n^{4}+3n}_{1}\times T^{2n^{2}+2n+1}_{2}\times T^{3n^{2}+3n}_{3})_{n\in {\mathbb Z}}$
is ergodic for
![]() $\mu ^{\otimes 4}$
, and both sequences
$\mu ^{\otimes 4}$
, and both sequences
![]() $(T^{-n^{4}+n^{2}-3n}_{1})_{n\in {\mathbb Z}}$
and
$(T^{-n^{4}+n^{2}-3n}_{1})_{n\in {\mathbb Z}}$
and
![]() $((T^{2}_{2}T_{3}^{-3})^{n^{2}+n})_{n\in {\mathbb Z}}$
are ergodic for
$((T^{2}_{2}T_{3}^{-3})^{n^{2}+n})_{n\in {\mathbb Z}}$
are ergodic for
![]() $\mu $
.
$\mu $
.
Another direction for the joint ergodicity problem is verifying whether condition (C1) implies condition (C2) in Conjecture 1.3. Namely, assume that
![]() $(T_{p_{1}(n)}\times \cdots \times T_{p_{k}(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for
$(T_{p_{1}(n)}\times \cdots \times T_{p_{k}(n)})_{n\in \mathbb {Z}^{L}}$
is ergodic for
![]() $\mu ^{\otimes k}$
to find a condition, say (P), of certain sequences of actions to be ergodic, under which we have that
$\mu ^{\otimes k}$
to find a condition, say (P), of certain sequences of actions to be ergodic, under which we have that
![]() $(T_{p_{1}(n)},\ldots ,T_{p_{k}(n)})_{n\in \mathbb {Z}^{L}}$
is jointly ergodic for
$(T_{p_{1}(n)},\ldots ,T_{p_{k}(n)})_{n\in \mathbb {Z}^{L}}$
is jointly ergodic for
![]() $\mu $
. By combining existing results from [Reference Host and Kra18, Reference Johnson20] (see also [Reference Donoso, Koutsogiannis and Sun7, Proposition 1.2]), (P) can be taken to be ‘
$\mu $
. By combining existing results from [Reference Host and Kra18, Reference Johnson20] (see also [Reference Donoso, Koutsogiannis and Sun7, Proposition 1.2]), (P) can be taken to be ‘
![]() $T_{g}$
is ergodic for
$T_{g}$
is ergodic for
![]() $\mu $
for all
$\mu $
for all
![]() $g\in {\mathbb Z}^{d}\backslash \{\mathbf {{0}}\}$
’. Denoting
$g\in {\mathbb Z}^{d}\backslash \{\mathbf {{0}}\}$
’. Denoting
![]() $p_{i}(n)=\sum _{v\in {\mathbb N}_0^{L},0\leq \vert v\vert \leq K}b_{i,v}n^{v}$
for some
$p_{i}(n)=\sum _{v\in {\mathbb N}_0^{L},0\leq \vert v\vert \leq K}b_{i,v}n^{v}$
for some
![]() $b_{i,v}\in \mathbb {Q}^{d}$
and
$b_{i,v}\in \mathbb {Q}^{d}$
and
![]() $K\in {\mathbb N}_0$
, this result was extended in [Reference Donoso, Koutsogiannis and Sun7, Theorem 1.3], where the previous property is replaced by ‘
$K\in {\mathbb N}_0$
, this result was extended in [Reference Donoso, Koutsogiannis and Sun7, Theorem 1.3], where the previous property is replaced by ‘
![]() $T_{g}$
is ergodic for
$T_{g}$
is ergodic for
![]() $\mu $
for all g that belongs to the finite set R’, where
$\mu $
for all g that belongs to the finite set R’, where
In this paper, we replace the latter condition with an even weaker one.
Theorem 2.9. Let
![]() $d,k,L\in \mathbb {N}, \mathbf {p}=(p_{1},\ldots , p_{k}), p_{1},\ldots , p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be a family of essentially distinct polynomials and
$d,k,L\in \mathbb {N}, \mathbf {p}=(p_{1},\ldots , p_{k}), p_{1},\ldots , p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be a family of essentially distinct polynomials and
![]() $(X,\ \mathcal {B},\ \mu ,\ (T_{g})_{g\in \mathbb {Z}^{d}})$
a
$(X,\ \mathcal {B},\ \mu ,\ (T_{g})_{g\in \mathbb {Z}^{d}})$
a
![]() $\mathbb {Z}^{d}$
-system. Then,
$\mathbb {Z}^{d}$
-system. Then,
![]() $(T_{p_{1}(n)},\ldots , T_{p_{k}(n)})_{n\in {\mathbb Z}^{L}}$
is jointly ergodic for
$(T_{p_{1}(n)},\ldots , T_{p_{k}(n)})_{n\in {\mathbb Z}^{L}}$
is jointly ergodic for
![]() $\mu $
if both of the following conditions hold:
$\mu $
if both of the following conditions hold:
-
(i)
 $G_{i,j}(\mathbf {p})$
is ergodic for
$G_{i,j}(\mathbf {p})$
is ergodic for
 $\mu $
for all
$\mu $
for all
 $0\leq i,j\leq k,i\neq j$
;
$0\leq i,j\leq k,i\neq j$
; -
(ii)
 $(T_{p_{1}(n)}\times \cdots \times T_{p_{k}(n)})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{p_{1}(n)}\times \cdots \times T_{p_{k}(n)})_{n\in {\mathbb Z}^{L}}$
is ergodic for
 $\mu ^{\otimes k}$
.
$\mu ^{\otimes k}$
.
The last example for this section reflects the stronger nature of the previous theorem compared to what was previously known.
Example 2.10. Let
![]() $(X,\mathcal {B},\mu ,T_{1},T_2,T_3,T_{4})$
be a system. Then, [Reference Donoso, Koutsogiannis and Sun7, Theorem 1.3] implies that
$(X,\mathcal {B},\mu ,T_{1},T_2,T_3,T_{4})$
be a system. Then, [Reference Donoso, Koutsogiannis and Sun7, Theorem 1.3] implies that
![]() $(T^{n^2}_{1} T^{n}_{2},T^{n^2}_{3} T^{n}_{4})_{n\in {\mathbb Z}}$
is jointly ergodic if
$(T^{n^2}_{1} T^{n}_{2},T^{n^2}_{3} T^{n}_{4})_{n\in {\mathbb Z}}$
is jointly ergodic if
![]() $((T^{n^2}_{1} T^n_2)\times (T^{n^2}_3 T^n_{4}))_{n\in \mathbb {Z}}$
is ergodic for
$((T^{n^2}_{1} T^n_2)\times (T^{n^2}_3 T^n_{4}))_{n\in \mathbb {Z}}$
is ergodic for
![]() $\mu ^{\otimes 2}$
, and all
$\mu ^{\otimes 2}$
, and all
![]() $T_{1},T_{2},T_{3},T_{4},T_{1}T_{3}^{-1},T_{2}T_{4}^{-1}$
are ergodic for
$T_{1},T_{2},T_{3},T_{4},T_{1}T_{3}^{-1},T_{2}T_{4}^{-1}$
are ergodic for
![]() $\mu $
. Using Theorem 2.9, we conclude that
$\mu $
. Using Theorem 2.9, we conclude that
![]() $(T^{n^2}_{1} T^{n}_{2}, T^{n^2}_{3} T^{n}_{4})_{n\in {\mathbb Z}}$
is jointly ergodic if we instead only assume that
$(T^{n^2}_{1} T^{n}_{2}, T^{n^2}_{3} T^{n}_{4})_{n\in {\mathbb Z}}$
is jointly ergodic if we instead only assume that
![]() $((T^{n^2}_{1} T^n_2)\times (T^{n^2}_3 T^n_{4}))_{n\in \mathbb {Z}}$
is ergodic for
$((T^{n^2}_{1} T^n_2)\times (T^{n^2}_3 T^n_{4}))_{n\in \mathbb {Z}}$
is ergodic for
![]() $\mu ^{\otimes 2}$
, and all
$\mu ^{\otimes 2}$
, and all
![]() $T_{1},T_{3},T_{1}T_{3}^{-1}$
are ergodic for
$T_{1},T_{3},T_{1}T_{3}^{-1}$
are ergodic for
![]() $\mu $
.
$\mu $
.
Unfortunately, Theorem 2.9 does not imply Conjecture 1.3 for the pair
![]() $(T^{n^2}_{1} T^{n}_{2}, T^{n^2}_{3} T^{n}_{4})_{n\in {\mathbb Z}}$
. This is because
$(T^{n^2}_{1} T^{n}_{2}, T^{n^2}_{3} T^{n}_{4})_{n\in {\mathbb Z}}$
. This is because
![]() $T_{1},T_{3},T_{1}T_{3}^{-1}$
being ergodic for
$T_{1},T_{3},T_{1}T_{3}^{-1}$
being ergodic for
![]() $\mu $
is independent of
$\mu $
is independent of
![]() $((T_{1}T_{3}^{-1})^{n^2} (T_{2}T_{4}^{-1})^{n})_{n\in {\mathbb Z}}$
being ergodic for
$((T_{1}T_{3}^{-1})^{n^2} (T_{2}T_{4}^{-1})^{n})_{n\in {\mathbb Z}}$
being ergodic for
![]() $\mu $
. For example, if
$\mu $
. For example, if
![]() $T_{1}=T_{3}=T_{4}=\mathrm {id}$
and
$T_{1}=T_{3}=T_{4}=\mathrm {id}$
and
![]() $T_{2}$
is any ergodic transformation, then
$T_{2}$
is any ergodic transformation, then
![]() $((T_{1}T_{3}^{-1})^{n^2} (T_{2}T_{4}^{-1})^{n})_{n\in {\mathbb Z}}$
is ergodic for
$((T_{1}T_{3}^{-1})^{n^2} (T_{2}T_{4}^{-1})^{n})_{n\in {\mathbb Z}}$
is ergodic for
![]() $\mu $
but
$\mu $
but
![]() $T_{1},T_{3},T_{1}T_{3}^{-1}$
are not. However, if
$T_{1},T_{3},T_{1}T_{3}^{-1}$
are not. However, if
![]() $X=\{0,\ldots ,6\}$
with
$X=\{0,\ldots ,6\}$
with
![]() $\mu (\{i\})=1/7$
,
$\mu (\{i\})=1/7$
,
![]() $T_{1}x:=x+1\ \mod 7$
,
$T_{1}x:=x+1\ \mod 7$
,
![]() $T_{3}=T_{1}^{2}$
, and
$T_{3}=T_{1}^{2}$
, and
![]() $T_{2}=T_{4}=\mathrm {id}$
, then
$T_{2}=T_{4}=\mathrm {id}$
, then
![]() $T_{1},T_{3},T_{1}T_{3}^{-1}$
are ergodic for
$T_{1},T_{3},T_{1}T_{3}^{-1}$
are ergodic for
![]() $\mu $
but
$\mu $
but
![]() $((T_{1}T_{3}^{-1})^{n^2} (T_{2}T_{4}^{-1})^{n})_{n\in {\mathbb Z}}$
is not.
$((T_{1}T_{3}^{-1})^{n^2} (T_{2}T_{4}^{-1})^{n})_{n\in {\mathbb Z}}$
is not.
2.3 Strategy of the paper
The central ingredient in proving the main results of the paper (Theorems 2.2, 2.5, and 2.9) is to find proper characteristic factors for the limit of the average in equation (4), that is, sub-
![]() $\sigma $
-algebras
$\sigma $
-algebras
![]() $\mathcal {D}_{1},\ldots ,\mathcal {D}_{k}$
of
$\mathcal {D}_{1},\ldots ,\mathcal {D}_{k}$
of
![]() $\mathcal {B}$
such that the average in equation (4) remains invariant if we replace each
$\mathcal {B}$
such that the average in equation (4) remains invariant if we replace each
![]() $f_{i}$
by its conditional expectation (see below for the definition) with respect to
$f_{i}$
by its conditional expectation (see below for the definition) with respect to
![]() $\mathcal {D}_{i}$
. An important type of characteristic factor, called the Host–Kra characteristic factor, was invented in [Reference Host and Kra18] to study multiple averages for
$\mathcal {D}_{i}$
. An important type of characteristic factor, called the Host–Kra characteristic factor, was invented in [Reference Host and Kra18] to study multiple averages for
![]() ${\mathbb Z}$
-systems (see below for the definition of these factors). This concept was generalized to systems with commuting transformations in [Reference Host17] (see also [Reference Sun31]).
${\mathbb Z}$
-systems (see below for the definition of these factors). This concept was generalized to systems with commuting transformations in [Reference Host17] (see also [Reference Sun31]).
To introduce the main tool used in our results (Theorem 2.11), special cases of which have been studied extensively in the past (see for example [Reference Chu, Frantzikinakis and Host6, Reference Frantzikinakis and Kra14, Reference Host17, Reference Host and Kra18, Reference Johnson20]), we need to introduce the machinery of Host–Kra seminorms and factors.
Host–Kra seminorms and their associated factors are arguably the main tools used to analyze the behavior of multiple averages and correlation sequences. In what follows, we give general results about these seminorms and factors, following the notation used in [Reference Donoso, Koutsogiannis and Sun7].
We first recall the notions of a factor and of the conditional expectation with respect to a factor. We say that the
![]() ${\mathbb Z}^d$
-system
${\mathbb Z}^d$
-system
![]() $(Y,\mathcal {D},\nu ,(S_{g})_{g\in {\mathbb Z}^d})$
is a factor of
$(Y,\mathcal {D},\nu ,(S_{g})_{g\in {\mathbb Z}^d})$
is a factor of
![]() $(X,\mathcal {B},\mu ,(T_{g})_{g\in {\mathbb Z}^d})$
if there exists a measurable map
$(X,\mathcal {B},\mu ,(T_{g})_{g\in {\mathbb Z}^d})$
if there exists a measurable map
![]() $\pi \colon X\to Y$
such that
$\pi \colon X\to Y$
such that
![]() $\mu (\pi ^{-1}(A))=\nu (A)$
for all
$\mu (\pi ^{-1}(A))=\nu (A)$
for all
![]() $A\in \mathcal {D}$
, and
$A\in \mathcal {D}$
, and
![]() $\pi \circ T_{g}=S_{g}\circ \pi $
for all
$\pi \circ T_{g}=S_{g}\circ \pi $
for all
![]() $g\in {\mathbb Z}^{d}$
.
$g\in {\mathbb Z}^{d}$
.
A factor
![]() $(Y,\mathcal {D},\nu ,(S_{g})_{g\in {\mathbb Z}^d})$
of
$(Y,\mathcal {D},\nu ,(S_{g})_{g\in {\mathbb Z}^d})$
of
![]() $(X,\mathcal {B},\mu ,(T_{g})_{g\in {\mathbb Z}^d})$
can be identified with an invariant sub-
$(X,\mathcal {B},\mu ,(T_{g})_{g\in {\mathbb Z}^d})$
can be identified with an invariant sub-
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {B}'$
of
$\mathcal {B}'$
of
![]() $\mathcal {B}$
by setting
$\mathcal {B}$
by setting ![]() . Given two
. Given two
![]() $\sigma $
-algebras,
$\sigma $
-algebras,
![]() $\mathcal {B}_1$
and
$\mathcal {B}_1$
and
![]() $\mathcal {B}_2$
, their joining
$\mathcal {B}_2$
, their joining
![]() $\mathcal {B}_1\vee \mathcal {B}_2$
is the
$\mathcal {B}_1\vee \mathcal {B}_2$
is the
![]() $\sigma $
-algebra generated by
$\sigma $
-algebra generated by
![]() $B_1\cap B_2$
for all
$B_1\cap B_2$
for all
![]() $B_1\in \mathcal {B}_1$
and
$B_1\in \mathcal {B}_1$
and
![]() $B_2\in \mathcal {B}_2$
, that is, the smallest
$B_2\in \mathcal {B}_2$
, that is, the smallest
![]() $\sigma $
-algebra containing both
$\sigma $
-algebra containing both
![]() $\mathcal {B}_1$
and
$\mathcal {B}_1$
and
![]() $\mathcal {B}_2$
.
$\mathcal {B}_2$
.
Given a factor
![]() $\pi \colon (X,\mathcal {B},\mu ) \to (Y,\mathcal {D},\nu )$
and a function
$\pi \colon (X,\mathcal {B},\mu ) \to (Y,\mathcal {D},\nu )$
and a function
![]() $f\in L^{2}(\mu )$
, the conditional expectation of f with respect to Y is the function
$f\in L^{2}(\mu )$
, the conditional expectation of f with respect to Y is the function
![]() $g\in L^{2}(\nu ),$
which we denote by
$g\in L^{2}(\nu ),$
which we denote by
![]() $\mathbb {E}(f \mid Y),$
with the property
$\mathbb {E}(f \mid Y),$
with the property
Let
![]() $(X,\mathcal {B},\mu )$
be a probability space and let
$(X,\mathcal {B},\mu )$
be a probability space and let
![]() $\mathcal {B}_1$
be a sub-
$\mathcal {B}_1$
be a sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $\mathcal {B}$
. The relatively independent joining of
$\mathcal {B}$
. The relatively independent joining of
![]() $(X,\mathcal {B},\mu )$
with itself with respect to
$(X,\mathcal {B},\mu )$
with itself with respect to
![]() $\mathcal {B}_1$
is the probability space
$\mathcal {B}_1$
is the probability space
![]() $(X\times X, \mathcal {B} \otimes \mathcal {B}, \mu \times _{\mathcal {B}_1} \mu )$
, where the measure
$(X\times X, \mathcal {B} \otimes \mathcal {B}, \mu \times _{\mathcal {B}_1} \mu )$
, where the measure
![]() $\mu \times _{\mathcal {B}_1} \mu $
is given by the formula:
$\mu \times _{\mathcal {B}_1} \mu $
is given by the formula:
for all
![]() $f_1, f_{2} \in L^{\infty }(\mu )$
.
$f_1, f_{2} \in L^{\infty }(\mu )$
.
For a G-system
![]() $\mathbf {X}=(X,\mathcal {B},\mu ,(T_{g})_{g\in G})$
, if H is a subgroup of
$\mathbf {X}=(X,\mathcal {B},\mu ,(T_{g})_{g\in G})$
, if H is a subgroup of
![]() $G,$
we denote by
$G,$
we denote by
![]() $\mathcal {I}(H)(\mathbf {X})$
the set of
$\mathcal {I}(H)(\mathbf {X})$
the set of
![]() $A\in \mathcal {B}$
such that
$A\in \mathcal {B}$
such that
![]() $T_{g}A=A$
for all
$T_{g}A=A$
for all
![]() $g\in H$
. When there is no confusion, we write
$g\in H$
. When there is no confusion, we write
![]() $\mathcal {I}(H)$
.
$\mathcal {I}(H)$
.
For a
![]() ${\mathbb Z}^d$
-system
${\mathbb Z}^d$
-system
![]() $(X,\mathcal {B},\mu ,(T_{g})_{g\in {\mathbb Z}^d})$
and
$(X,\mathcal {B},\mu ,(T_{g})_{g\in {\mathbb Z}^d})$
and
![]() $H_1,\ldots ,H_k$
subgroups of
$H_1,\ldots ,H_k$
subgroups of
![]() ${\mathbb Z}^d,$
define
${\mathbb Z}^d,$
define
and for
![]() $k>1$
, let
$k>1$
, let
where
![]() $H^{[k-1]}_{k}$
denotes the subgroup of
$H^{[k-1]}_{k}$
denotes the subgroup of
![]() $({\mathbb Z}^{d})^{2^{k-1}}$
consisting of all the elements of the form
$({\mathbb Z}^{d})^{2^{k-1}}$
consisting of all the elements of the form
![]() $(h_{k},\ldots , h_{k})$
(
$(h_{k},\ldots , h_{k})$
(
![]() $2^{k-1}$
copies of
$2^{k-1}$
copies of
![]() $h_{k}$
) for some
$h_{k}$
) for some
![]() $h_{k}\in H_{k}$
. The characteristic factor
$h_{k}\in H_{k}$
. The characteristic factor
![]() $Z_{H_{1},\ldots ,H_{k}}(\mathbf {X})$
is defined to be the sub-
$Z_{H_{1},\ldots ,H_{k}}(\mathbf {X})$
is defined to be the sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $\mathcal {B}$
characterized by
$\mathcal {B}$
characterized by

for all
![]() $f \in L^{\infty }(\mu )$
, where
$f \in L^{\infty }(\mu )$
, where
![]() $X^{[k]}=X\times \cdots \times X$
(
$X^{[k]}=X\times \cdots \times X$
(
![]() $2^k$
copies of X),
$2^k$
copies of X),
![]() $\vert \epsilon \vert =\epsilon _{1}+\cdots +\epsilon _{k}$
for
$\vert \epsilon \vert =\epsilon _{1}+\cdots +\epsilon _{k}$
for
![]() $\epsilon =(\epsilon _{1},\ldots ,\epsilon _{k})\in \{0,1\}^{k}$
, and
$\epsilon =(\epsilon _{1},\ldots ,\epsilon _{k})\in \{0,1\}^{k}$
, and
![]() $\mathcal {C}^{2r+1}f=\overline {f},$
the complex conjugate of f,
$\mathcal {C}^{2r+1}f=\overline {f},$
the complex conjugate of f,
![]() $\mathcal {C}^{2r}f=f$
for all
$\mathcal {C}^{2r}f=f$
for all
![]() $r\in {\mathbb Z}$
. The quantity
$r\in {\mathbb Z}$
. The quantity
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H_1,\ldots ,H_k}$
denotes the Host–Kra seminorm of f with respect to the subgroups
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H_1,\ldots ,H_k}$
denotes the Host–Kra seminorm of f with respect to the subgroups
![]() $H_1,\ldots ,H_k$
. Similar to the proof of [Reference Host17, Lemma 4] or [Reference Host and Kra18, Lemma 4.3], one can show that
$H_1,\ldots ,H_k$
. Similar to the proof of [Reference Host17, Lemma 4] or [Reference Host and Kra18, Lemma 4.3], one can show that
![]() $Z_{H_{1},\ldots ,H_{k}}(\mathbf {X})$
is well defined.
$Z_{H_{1},\ldots ,H_{k}}(\mathbf {X})$
is well defined.
Theorem 2.11. Let
![]() $d,k,K,L\in \mathbb {N}, \mathbf {p}=(p_{1},\ldots , p_{k}), p_{1},\ldots , p_{k}\in \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be a family of essentially distinct polynomials of degrees at most
$d,k,K,L\in \mathbb {N}, \mathbf {p}=(p_{1},\ldots , p_{k}), p_{1},\ldots , p_{k}\in \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be a family of essentially distinct polynomials of degrees at most
![]() $K.$
There exists
$K.$
There exists
![]() $D\in \mathbb {N}_0$
depending only on
$D\in \mathbb {N}_0$
depending only on
![]() $d,k,K,L$
such that for every
$d,k,K,L$
such that for every
![]() $\mathbb {Z}^{d}$
-system
$\mathbb {Z}^{d}$
-system
![]() $\mathbf {X}=(X,\mathcal {B},\mu , (T_{n})_{n\in \mathbb {Z}^{d}})$
, every
$\mathbf {X}=(X,\mathcal {B},\mu , (T_{n})_{n\in \mathbb {Z}^{d}})$
, every
![]() $f_{1},\ldots , f_{k}\in L^{\infty }(\mu )$
, and every Følner sequence
$f_{1},\ldots , f_{k}\in L^{\infty }(\mu )$
, and every Følner sequence
![]() $(I_{N})_{N\in {\mathbb N}}$
of
$(I_{N})_{N\in {\mathbb N}}$
of
![]() ${\mathbb Z}^{L}$
, if
${\mathbb Z}^{L}$
, if
![]() $f_{i}$
is orthogonal to the Host–Kra characteristic factor
$f_{i}$
is orthogonal to the Host–Kra characteristic factor
![]() ${Z}_{\{G_{i,j}(\mathbf {p})\}^{\times D}_{0\leq j\leq k, j\neq i}}(\mathbf {X})$
for some
${Z}_{\{G_{i,j}(\mathbf {p})\}^{\times D}_{0\leq j\leq k, j\neq i}}(\mathbf {X})$
for some
![]() $1\leq i\leq k$
(that is, the conditional expectation of
$1\leq i\leq k$
(that is, the conditional expectation of
![]() $f_{i}$
under
$f_{i}$
under
![]() ${Z}_{\{G_{i,j}(\mathbf {p})\}^{\times D}_{0\leq j\leq k, j\neq i}}(\mathbf {X})$
is
${Z}_{\{G_{i,j}(\mathbf {p})\}^{\times D}_{0\leq j\leq k, j\neq i}}(\mathbf {X})$
is
![]() $0$
), then we have that
$0$
), then we have that
 $$ \begin{align} \lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^k T_{p_{i}(n)}f_i=0. \end{align} $$
$$ \begin{align} \lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^k T_{p_{i}(n)}f_i=0. \end{align} $$
In particular, if for some
![]() $1\leq i\leq k$
,
$1\leq i\leq k$
,
![]() $G_{i,j}(\mathbf {p})$
is ergodic for
$G_{i,j}(\mathbf {p})$
is ergodic for
![]() $\mu $
for all
$\mu $
for all
![]() $0\leq j\leq k, j\neq i$
and
$0\leq j\leq k, j\neq i$
and
![]() $f_{i}$
is orthogonal to the Host–Kra characteristic factor
$f_{i}$
is orthogonal to the Host–Kra characteristic factor
![]() ${Z}_{({\mathbb Z}^{d})^{\times kD}}(\mathbf {X})$
, then equation (10) holds.
${Z}_{({\mathbb Z}^{d})^{\times kD}}(\mathbf {X})$
, then equation (10) holds.
It is worth noting that the factor
![]() ${Z}_{\{G_{i,j}(\mathbf {p})\}^{\times D}_{0\leq j\leq k, j\neq i}}(\mathbf {X})$
we obtain in Theorem 2.11 is not optimal, but it is good enough for our purposes.
${Z}_{\{G_{i,j}(\mathbf {p})\}^{\times D}_{0\leq j\leq k, j\neq i}}(\mathbf {X})$
we obtain in Theorem 2.11 is not optimal, but it is good enough for our purposes.
A special case of Theorem 2.11 was proved in [Reference Donoso, Koutsogiannis and Sun7, Theorem 5.1]. In particular, Theorem 2.11 generalizes [Reference Donoso, Koutsogiannis and Sun7, Theorem 5.1] in the following ways.
-
(I) The characteristic factor obtained in Theorem 2.11 is of finite step, whereas that in [Reference Donoso, Koutsogiannis and Sun7, Theorem 5.1] is of infinite step.
-
(II) The groups
 $G_{i,j}(\mathbf {p})$
involved in Theorem 2.11 are larger than those in [Reference Donoso, Koutsogiannis and Sun7, Theorem 5.1], which makes the characteristic factors in Theorem 2.11 smaller.
$G_{i,j}(\mathbf {p})$
involved in Theorem 2.11 are larger than those in [Reference Donoso, Koutsogiannis and Sun7, Theorem 5.1], which makes the characteristic factors in Theorem 2.11 smaller.
We remark that the aforementioned technical distinctions have significant influences on the applications of Theorem 2.11. First, the essential reason why one cannot directly use [Reference Donoso, Koutsogiannis and Sun7, Theorem 5.1] to improve [Reference Ferré Moragues9, Theorem 1.5] is that the method used in [Reference Ferré Moragues9] requires a characteristic factor of finite step. This problem is resolved by generalization (I), enabling us to extend [Reference Ferré Moragues9, Theorem 1.5] in this paper. Second, [Reference Donoso, Koutsogiannis and Sun7, Theorem 5.1] does not provide a strong enough characteristic factor in certain circumstances. For example, in the case of Example 2.6, [Reference Chu, Frantzikinakis and Host6, Theorem 6.5] suggests that the Host–Kra seminorms controlling equation (10) depend only on the transformations
![]() $T_{1},\ldots ,T_{k}$
, whereas the upper bound provided by [Reference Donoso, Koutsogiannis and Sun7, Theorem 5.1] depends not only on the transformations
$T_{1},\ldots ,T_{k}$
, whereas the upper bound provided by [Reference Donoso, Koutsogiannis and Sun7, Theorem 5.1] depends not only on the transformations
![]() $T_{1},\ldots ,T_{k}$
but also on many compositions of them. With the help of generalizations (I) and (II), we are able to obtain (and generalize) the aforementioned upper bound of [Reference Chu, Frantzikinakis and Host6, Theorem 6.5].
$T_{1},\ldots ,T_{k}$
but also on many compositions of them. With the help of generalizations (I) and (II), we are able to obtain (and generalize) the aforementioned upper bound of [Reference Chu, Frantzikinakis and Host6, Theorem 6.5].
Roughly speaking, the achievement of generalization (I) relies on a sophisticated development of a Bessel-type inequality first obtained by Tao and Ziegler in [Reference Tao and Ziegler33, Proposition 3.6]. The most technical part of this paper is the approach we use to get generalization (II). In [Reference Donoso, Koutsogiannis and Sun7], a method was introduced to keep track of the coefficients of the polynomials while running a variation of the polynomial exhaustion technique (PET) induction. However, the tracking provided there is not strong enough to imply Theorem 2.11. To overcome this difficulty, we introduce more sophisticated machinery to have a better control of the coefficients.
The paper is organized as follows. We provide some background material in §3. In §4, we present the variation of PET induction that we use. In §5, we address how generalizations (I) and (II) above can be achieved with Propositions 5.2 and 5.4, which improve Propositions 5.6 and 5.5 of [Reference Donoso, Koutsogiannis and Sun7], respectively. We conclude the section by proving Theorem 2.11. This is the bulk of the paper. In §6, we use Theorem 2.11 to deduce Theorems 2.2, 2.5, and 2.9, which are the main results of the paper. We conclude with some discussions on future directions in §7.
2.4 Notation
We denote by
![]() $\mathbb {N}, \mathbb {N}_0, \mathbb {Z}, \mathbb {Q}, \mathbb {R}$
, and
$\mathbb {N}, \mathbb {N}_0, \mathbb {Z}, \mathbb {Q}, \mathbb {R}$
, and
![]() $\mathbb {C}$
the sets of positive integers, non-negative integers, integers, rational numbers, real numbers, and complex numbers, respectively. If X is a set and
$\mathbb {C}$
the sets of positive integers, non-negative integers, integers, rational numbers, real numbers, and complex numbers, respectively. If X is a set and
![]() $d\in \mathbb {N}$
,
$d\in \mathbb {N}$
,
![]() $X^d$
denotes the Cartesian product
$X^d$
denotes the Cartesian product
![]() $X\times \cdots \times X$
of d copies of X.
$X\times \cdots \times X$
of d copies of X.
We will denote by
![]() $e_i$
the vector that has
$e_i$
the vector that has
![]() $1$
as its ith coordinate and
$1$
as its ith coordinate and
![]() $0$
elsewhere. We use in general lower-case letters to symbolize both numbers and vectors but bold letters to symbolize vectors of vectors to highlight this exact fact. The only exception to this convention is the vector
$0$
elsewhere. We use in general lower-case letters to symbolize both numbers and vectors but bold letters to symbolize vectors of vectors to highlight this exact fact. The only exception to this convention is the vector
![]() $\mathbf {0}$
(that is, the vector with coordinates only
$\mathbf {0}$
(that is, the vector with coordinates only
![]() $0$
) which we always symbolize in bold.
$0$
) which we always symbolize in bold.
Throughout this article, we use the following notation for averages. Let
![]() $(a(n))_{n\in {\mathbb Z}^L}$
be a sequence of complex numbers, or a sequence of measurable functions on a probability space
$(a(n))_{n\in {\mathbb Z}^L}$
be a sequence of complex numbers, or a sequence of measurable functions on a probability space
![]() $(X,\mathcal {B},\mu )$
. We let:
$(X,\mathcal {B},\mu )$
. We let:
![]()
![]() (we use the symbol
(we use the symbol
![]() $\square $
to highlight the fact that the averages are taken along the boxes
$\square $
to highlight the fact that the averages are taken along the boxes
![]() $[-N,N]^{L}$
);
$[-N,N]^{L}$
);
![]()
![]() and
and
![]() It is worth noticing that if the limit
It is worth noticing that if the limit
![]() $\lim _{N\to \infty } \mathbb {E}_{n\in I_N} a(n)$
exists for all Følner sequences (in
$\lim _{N\to \infty } \mathbb {E}_{n\in I_N} a(n)$
exists for all Følner sequences (in
![]() ${\mathbb Z}^L$
), then this limit does not depend on the chosen Følner sequence.
${\mathbb Z}^L$
), then this limit does not depend on the chosen Følner sequence.
We also consider iterated averages. Let
![]() $(a(h_{1},\ldots ,h_{s}))_{h_{1},\ldots ,h_{s}\in {\mathbb Z}^L}$
be a multiparameter sequence. We let
$(a(h_{1},\ldots ,h_{s}))_{h_{1},\ldots ,h_{s}\in {\mathbb Z}^L}$
be a multiparameter sequence. We let
and adopt similar conventions for
![]() $\mathbb {E}_{h_{1},\ldots ,h_{s}\in \mathbb {Z}^{L}}$
,
$\mathbb {E}_{h_{1},\ldots ,h_{s}\in \mathbb {Z}^{L}}$
,
![]() ${\overline {\mathbb {E}}}^{\square }_{h_{1},\ldots ,h_{s}\in \mathbb {Z}^{L}}$
, and
${\overline {\mathbb {E}}}^{\square }_{h_{1},\ldots ,h_{s}\in \mathbb {Z}^{L}}$
, and
![]() $\mathbb {E}^{\square }_{h_{1},\ldots ,h_{s}\in \mathbb {Z}^{L}}$
.
$\mathbb {E}^{\square }_{h_{1},\ldots ,h_{s}\in \mathbb {Z}^{L}}$
.
We end this section by recalling the notion of a system indexed by a countable abelian group
![]() $(G,+)$
. We say that a tuple
$(G,+)$
. We say that a tuple
![]() $(X,\mathcal {B},\mu ,(T_{g})_{g\in G})$
is a G-measure-preserving system (or a G-system) if
$(X,\mathcal {B},\mu ,(T_{g})_{g\in G})$
is a G-measure-preserving system (or a G-system) if
![]() $(X,\mathcal {B},\mu )$
is a probability space and
$(X,\mathcal {B},\mu )$
is a probability space and
![]() $T_{g}\colon X\to X$
are measurable, measure-preserving transformations on X such that
$T_{g}\colon X\to X$
are measurable, measure-preserving transformations on X such that
![]() $T_{e_{G}}=\mathrm {id}$
(
$T_{e_{G}}=\mathrm {id}$
(
![]() $e_G$
is the identity element of G) and
$e_G$
is the identity element of G) and
![]() $T_{g}\circ T_{h}=T_{g+h}$
for all
$T_{g}\circ T_{h}=T_{g+h}$
for all
![]() $g,h\in G$
. A G-system will be called ergodic if for any
$g,h\in G$
. A G-system will be called ergodic if for any
![]() $A\in \mathcal {B}$
such that
$A\in \mathcal {B}$
such that
![]() $T_{g}A=A$
for all
$T_{g}A=A$
for all
![]() $g\in G$
, we have that
$g\in G$
, we have that
![]() $\mu (A)\in \{0,1\}$
. In this paper, we are mostly concerned about
$\mu (A)\in \{0,1\}$
. In this paper, we are mostly concerned about
![]() ${\mathbb Z}^{d}$
-systems and
${\mathbb Z}^{d}$
-systems and
![]() $L^2(\mu )$
-norm limits of (multiple) ergodic averages. For the corresponding norm, when it is clear from the context, we will write
$L^2(\mu )$
-norm limits of (multiple) ergodic averages. For the corresponding norm, when it is clear from the context, we will write
![]() $\Vert {\cdot} \Vert _2$
instead of
$\Vert {\cdot} \Vert _2$
instead of
![]() $\Vert {\cdot} \Vert _{L^2(\mu )}$
.
$\Vert {\cdot} \Vert _{L^2(\mu )}$
.
3 Background material
In this section, we recall some background material and prove some intermediate results that will be used later throughout the paper.
We summarize some basic properties of the Host–Kra seminorms and their associated factors.
Proposition 3.1. [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.4]
Let
![]() $\mathbf {X}=(X,\mathcal {B},\mu ,(T_{g})_{g\in {\mathbb Z}^d})$
be a
$\mathbf {X}=(X,\mathcal {B},\mu ,(T_{g})_{g\in {\mathbb Z}^d})$
be a
![]() ${\mathbb Z}^{d}$
-system,
${\mathbb Z}^{d}$
-system,
![]() $H_{1},\ldots ,H_{k},H'$
be subgroups of
$H_{1},\ldots ,H_{k},H'$
be subgroups of
![]() ${\mathbb Z}^{d}$
and
${\mathbb Z}^{d}$
and
![]() $f\in L^{\infty }(\mu )$
.
$f\in L^{\infty }(\mu )$
.
-
(i) For every permutation
 $\sigma \colon \{1,\ldots ,k\}\to \{1,\ldots ,k\}$
, we have that
$\sigma \colon \{1,\ldots ,k\}\to \{1,\ldots ,k\}$
, we have that  $$ \begin{align*} Z_{H_{1},\ldots,H_{k}}(\mathbf{X})=Z_{H_{\sigma(1)},\ldots,H_{\sigma(k)}}(\mathbf{X}), \end{align*} $$
$$ \begin{align*} Z_{H_{1},\ldots,H_{k}}(\mathbf{X})=Z_{H_{\sigma(1)},\ldots,H_{\sigma(k)}}(\mathbf{X}), \end{align*} $$
and hence the corresponding seminorm does not depend on the particular order taken for the subgroups
 $H_1,\ldots ,H_k.$
$H_1,\ldots ,H_k.$
-
(ii) If
 $\mathcal {I}(H_{j})=\mathcal {I}(H')$
, then
$\mathcal {I}(H_{j})=\mathcal {I}(H')$
, then
 $Z_{H_{1},\ldots ,H_{j},\ldots ,H_{k}}(\mathbf {X})=Z_{H_{1},\ldots ,H_{j-1},H',H_{j+1},\ldots ,H_{k}}(\mathbf {X})$
.
$Z_{H_{1},\ldots ,H_{j},\ldots ,H_{k}}(\mathbf {X})=Z_{H_{1},\ldots ,H_{j-1},H',H_{j+1},\ldots ,H_{k}}(\mathbf {X})$
. -
(iii) For
 $k\geq 2$
, we have that
$k\geq 2$
, we have that  $$ \begin{align*}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2^{k}}_{H_{1},\ldots,H_{k}} =\mathbb{E}_{g\in H_{k}}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\cdot T_{g}\overline{f}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2^{k-1}}_{H_{1},\ldots,H_{k-1}},\end{align*} $$
$$ \begin{align*}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2^{k}}_{H_{1},\ldots,H_{k}} =\mathbb{E}_{g\in H_{k}}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\cdot T_{g}\overline{f}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2^{k-1}}_{H_{1},\ldots,H_{k-1}},\end{align*} $$
while for
 $k=1,$
$k=1,$
 $$ \begin{align*}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2}_{H_{1}} =\mathbb{E}_{g\in H_{1}}\int_{X} f\cdot T_{g}\overline{f}\,d\mu.\end{align*} $$
$$ \begin{align*}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2}_{H_{1}} =\mathbb{E}_{g\in H_{1}}\int_{X} f\cdot T_{g}\overline{f}\,d\mu.\end{align*} $$
-
(iv) Let
 $k\geq 2$
. If
$k\geq 2$
. If
 $H'\leq H_{j}$
is of finite index, then
$H'\leq H_{j}$
is of finite index, then  $$ \begin{align*}Z_{H_{1},\ldots,H_{j},\ldots,H_{k}}(\mathbf{X})=Z_{H_{1},\ldots,H_{j-1},H',H_{j+1},\ldots,H_{k}}(\mathbf{X}).\end{align*} $$
$$ \begin{align*}Z_{H_{1},\ldots,H_{j},\ldots,H_{k}}(\mathbf{X})=Z_{H_{1},\ldots,H_{j-1},H',H_{j+1},\ldots,H_{k}}(\mathbf{X}).\end{align*} $$
-
(v) If
 $H'\leq H_{j}$
, then
$H'\leq H_{j}$
, then
 $Z_{H_{1},\ldots ,H_{j},\ldots ,H_{k}}(\mathbf {X})\subseteq Z_{H_{1},\ldots ,H_{j-1},H',H_{j+1},\ldots ,H_{k}}(\mathbf {X})$
.
$Z_{H_{1},\ldots ,H_{j},\ldots ,H_{k}}(\mathbf {X})\subseteq Z_{H_{1},\ldots ,H_{j-1},H',H_{j+1},\ldots ,H_{k}}(\mathbf {X})$
. -
(vi) For
 $k\geq 2$
,
$k\geq 2$
,
 $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H_1,\ldots ,H_{k-1}}\leq \lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H_1,\ldots ,H_{k-1},H_k}$
and thus
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H_1,\ldots ,H_{k-1}}\leq \lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H_1,\ldots ,H_{k-1},H_k}$
and thus  $$ \begin{align*}Z_{H_1,\ldots,H_{k-1}}(\mathbf{X})\subseteq Z_{H_1,\ldots,H_{k-1},H_k}(\mathbf{X}).\end{align*} $$
$$ \begin{align*}Z_{H_1,\ldots,H_{k-1}}(\mathbf{X})\subseteq Z_{H_1,\ldots,H_{k-1},H_k}(\mathbf{X}).\end{align*} $$
-
(vii) For
 $k\geq 1$
, if
$k\geq 1$
, if
 $H_1',\ldots , H_k'$
are subgroups of
$H_1',\ldots , H_k'$
are subgroups of
 $ {\mathbb Z}^d$
, then
$ {\mathbb Z}^d$
, then  $$ \begin{align*}Z_{H_1,\ldots,H_k}(\mathbf{X}) \vee Z_{H_1',\ldots,H_k'}(\mathbf{X}) \subseteq Z_{H_1',\ldots,H_k',H_1,\ldots,H_k}(\mathbf{X}).\end{align*} $$
$$ \begin{align*}Z_{H_1,\ldots,H_k}(\mathbf{X}) \vee Z_{H_1',\ldots,H_k'}(\mathbf{X}) \subseteq Z_{H_1',\ldots,H_k',H_1,\ldots,H_k}(\mathbf{X}).\end{align*} $$
As an immediate corollary of Proposition 3.1(iv), we have the following corollary.
Corollary 3.2. [Reference Donoso, Koutsogiannis and Sun7, Corollary 2.5]
Let
![]() $H_{1},\ldots ,H_{k}$
be subgroups of
$H_{1},\ldots ,H_{k}$
be subgroups of
![]() ${\mathbb Z}^{d}$
. If the
${\mathbb Z}^{d}$
. If the
![]() $H_{i}$
-action
$H_{i}$
-action
![]() $(T_{g})_{g\in H_{i}}$
is ergodic on
$(T_{g})_{g\in H_{i}}$
is ergodic on
![]() $\mathbf {X}$
for all
$\mathbf {X}$
for all
![]() $1\leq i\leq k$
, then
$1\leq i\leq k$
, then
![]() $Z_{H_{1},\ldots ,H_{k}}(\mathbf {X})=Z_{{\mathbb Z}^{d},\ldots ,{\mathbb Z}^{d}}(\mathbf {X})$
.
$Z_{H_{1},\ldots ,H_{k}}(\mathbf {X})=Z_{{\mathbb Z}^{d},\ldots ,{\mathbb Z}^{d}}(\mathbf {X})$
.
Convention 3.3. Thanks to Proposition 3.1, we may adopt a flexible and convenient notation while writing the Host–Kra characteristic factors. For example, if
![]() $A=\{H_{1},H_{2}\}^{\times 3}$
, then the notation
$A=\{H_{1},H_{2}\}^{\times 3}$
, then the notation
![]() $Z_{A,H_{3},H^{\times 2}_{4},(H_{i})_{i=5,6}}(\mathbf {X})$
refers to
$Z_{A,H_{3},H^{\times 2}_{4},(H_{i})_{i=5,6}}(\mathbf {X})$
refers to
![]() $Z_{H_{1},H_{1},H_{1},H_{2},H_{2},H_{2},H_{3},H_{4},H_{4},H_{5},H_{6}}(\mathbf {X})$
(note that thanks to Proposition 3.1(i),
$Z_{H_{1},H_{1},H_{1},H_{2},H_{2},H_{2},H_{3},H_{4},H_{4},H_{5},H_{6}}(\mathbf {X})$
(note that thanks to Proposition 3.1(i),
![]() $Z_{A,H_{3},H^{\times 2}_{4},(H_{i})_{i=5,6}}(\mathbf {X})$
is well defined regardless of the ordering of A).
$Z_{A,H_{3},H^{\times 2}_{4},(H_{i})_{i=5,6}}(\mathbf {X})$
is well defined regardless of the ordering of A).
Recall that for a subgroup
![]() $H\subseteq {\mathbb Z}^d$
,
$H\subseteq {\mathbb Z}^d$
,
![]() $H^{[1]}$
denotes the subgroup
$H^{[1]}$
denotes the subgroup
![]() $\{ (h,h)\colon h\in H\}\subseteq {\mathbb Z}^d\times ~{\mathbb Z}^d$
.
$\{ (h,h)\colon h\in H\}\subseteq {\mathbb Z}^d\times ~{\mathbb Z}^d$
.
Lemma 3.4. Let
![]() $d \in {\mathbb N}$
. Let
$d \in {\mathbb N}$
. Let
![]() $(X,\mathcal {B},\mu ,(T_n)_{n\in {\mathbb Z}^d})$
be a
$(X,\mathcal {B},\mu ,(T_n)_{n\in {\mathbb Z}^d})$
be a
![]() ${\mathbb Z}^{d}$
-system and
${\mathbb Z}^{d}$
-system and
![]() $H_1,\ldots ,H_k,H$
be subgroups of
$H_1,\ldots ,H_k,H$
be subgroups of
![]() ${\mathbb Z}^d$
. Let
${\mathbb Z}^d$
. Let
![]() $f \in L^{\infty }(\mu )$
. Then,
$f \in L^{\infty }(\mu )$
. Then,
where in the left-hand side, we consider the product space
![]() $(X\times X,\mathcal {B}\otimes \mathcal {B},\mu \times \mu , (T_{m}\times T_{n})_{(m,n)\in \mathbb {Z}^{2d}})$
.
$(X\times X,\mathcal {B}\otimes \mathcal {B},\mu \times \mu , (T_{m}\times T_{n})_{(m,n)\in \mathbb {Z}^{2d}})$
.
Proof. We proceed by induction on k. For
![]() $k=1,$
using the Cauchy–Schwarz inequality, we have
$k=1,$
using the Cauchy–Schwarz inequality, we have
 $$ \begin{align*} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\otimes \overline{f}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_1^{[1]}}^2&= \mathbb{E}_{g\in H_1} \int f\otimes \overline{f} \cdot (T_g\times T_g )\overline{f}\otimes f \, d(\mu\times \mu) \\ &= \mathbb{E}_{g\in H_1} \bigg| \int T_g f \cdot \overline{f} d\mu \bigg|^2 = \mathbb{E}_{g\in H_1} \bigg| \int \mathbb{E}(T_g f \cdot \overline{f} | \mathcal{I}(H))\, d\mu \bigg|^2 \\ & \leq \mathbb{E}_{g\in H_1} \int |\mathbb{E}(T_g f \cdot \overline{f} | \mathcal{I}(H))|^2\, d\mu\\ &= \mathbb{E}_{g\in H_1} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert T_gf\cdot \overline{f}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H}^2\! =\! \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H,H_1}^4=\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_1,H}^4, \end{align*} $$
$$ \begin{align*} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\otimes \overline{f}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_1^{[1]}}^2&= \mathbb{E}_{g\in H_1} \int f\otimes \overline{f} \cdot (T_g\times T_g )\overline{f}\otimes f \, d(\mu\times \mu) \\ &= \mathbb{E}_{g\in H_1} \bigg| \int T_g f \cdot \overline{f} d\mu \bigg|^2 = \mathbb{E}_{g\in H_1} \bigg| \int \mathbb{E}(T_g f \cdot \overline{f} | \mathcal{I}(H))\, d\mu \bigg|^2 \\ & \leq \mathbb{E}_{g\in H_1} \int |\mathbb{E}(T_g f \cdot \overline{f} | \mathcal{I}(H))|^2\, d\mu\\ &= \mathbb{E}_{g\in H_1} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert T_gf\cdot \overline{f}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H}^2\! =\! \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H,H_1}^4=\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_1,H}^4, \end{align*} $$
where we used in the last two equalities Proposition 3.1(iii) and (i), respectively, from where we conclude the required relation by taking square roots.
Suppose that the result holds for
![]() $k-1$
. By Proposition 3.1(i) and the induction hypothesis,
$k-1$
. By Proposition 3.1(i) and the induction hypothesis,
 $$ \begin{align*} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f \otimes \overline{f}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_1^{[1]},\ldots,H_{k}^{[1]}}^{2^k} & =\mathbb{E}_{g\in H_k}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert (T_g\times T_{g}) f \otimes \overline{f} \cdot \overline{f} \otimes {f} \rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2^{k-1}}_{H_1^{[1]},\ldots,H_{k-1}^{[1]}} \\ & = \mathbb{E}_{g\in H_k}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert T_g f \cdot \overline{f} \otimes T_g \overline{f} \cdot f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2^{k-1}}_{H_1^{[1]},\ldots,H_{k-1}^{[1]}} \\ & \leq \mathbb{E}_{g\in H_k}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert T_g f \cdot \overline{f}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2^{k}}_{H_1,\ldots,H_{k-1},H} \\ & = \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_1,\ldots,H_{k-1},H,H_{k} } = \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_1,\ldots,H_{k-1},H_k,H} \end{align*} $$
$$ \begin{align*} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f \otimes \overline{f}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_1^{[1]},\ldots,H_{k}^{[1]}}^{2^k} & =\mathbb{E}_{g\in H_k}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert (T_g\times T_{g}) f \otimes \overline{f} \cdot \overline{f} \otimes {f} \rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2^{k-1}}_{H_1^{[1]},\ldots,H_{k-1}^{[1]}} \\ & = \mathbb{E}_{g\in H_k}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert T_g f \cdot \overline{f} \otimes T_g \overline{f} \cdot f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2^{k-1}}_{H_1^{[1]},\ldots,H_{k-1}^{[1]}} \\ & \leq \mathbb{E}_{g\in H_k}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert T_g f \cdot \overline{f}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{2^{k}}_{H_1,\ldots,H_{k-1},H} \\ & = \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_1,\ldots,H_{k-1},H,H_{k} } = \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_1,\ldots,H_{k-1},H_k,H} \end{align*} $$
and the claim follows.
3.1 Nilsystems, nilsequences, and structure theorem
Let
![]() $X=N/\Gamma $
, where N is a (k-step) nilpotent Lie group and
$X=N/\Gamma $
, where N is a (k-step) nilpotent Lie group and
![]() $\Gamma $
is a discrete cocompact subgroup of N. Let
$\Gamma $
is a discrete cocompact subgroup of N. Let
![]() $\mathcal {B}$
be the Borel
$\mathcal {B}$
be the Borel
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $X, \mu $
the normalized Haar measure on
$X, \mu $
the normalized Haar measure on
![]() $X,$
and for
$X,$
and for
![]() $n\in {\mathbb Z}^{d},$
let
$n\in {\mathbb Z}^{d},$
let
![]() ${T_{n}\colon X\to X}$
with
${T_{n}\colon X\to X}$
with
![]() $T_{n}x=b_{n}\cdot x$
for some group homomorphism
$T_{n}x=b_{n}\cdot x$
for some group homomorphism
![]() $n\mapsto b_{n}$
from
$n\mapsto b_{n}$
from
![]() ${\mathbb Z}^{d}$
to N. We say that
${\mathbb Z}^{d}$
to N. We say that
![]() $\mathbf {X}=(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^{d}})$
is a (k-step)
$\mathbf {X}=(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^{d}})$
is a (k-step)
![]() ${\mathbb Z}^{d}$
-nilsystem. For
${\mathbb Z}^{d}$
-nilsystem. For
![]() $k\geq 1$
, we say that
$k\geq 1$
, we say that
![]() $(a_{n})_{n\in {\mathbb Z}^{d}} \subseteq \mathbb {C}$
is a (k-step)
$(a_{n})_{n\in {\mathbb Z}^{d}} \subseteq \mathbb {C}$
is a (k-step)
![]() ${\mathbb Z}^{d}$
-nilsequence if there exist a (k-step)
${\mathbb Z}^{d}$
-nilsequence if there exist a (k-step)
![]() ${\mathbb Z}^{d}$
-nilsystem
${\mathbb Z}^{d}$
-nilsystem
![]() $(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^{d}})$
, a function
$(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^{d}})$
, a function
![]() $F \in C(X)$
and
$F \in C(X)$
and
![]() $x\in X$
such that
$x\in X$
such that
![]() $a_{n}=F(T_{n}x)$
for all
$a_{n}=F(T_{n}x)$
for all
![]() $n\in {\mathbb Z}^{d}$
. For
$n\in {\mathbb Z}^{d}$
. For
![]() $k=0$
, a
$k=0$
, a
![]() $0$
-step nilsequence is a constant sequence. An important reason which makes the Host–Kra characteristic factors powerful is their connection with nilsystems. The following is a slight generalization of [Reference Ziegler36, Theorem 3.7] (see [Reference Griesmer16, Lemma 4.4.3 and Theorem 4.10.1], or Proposition 3.1(ii) and [Reference Sun31, Theorem 3.7]), which is a higher dimensional version of the Host–Kra structure theorem [Reference Host and Kra18].
$0$
-step nilsequence is a constant sequence. An important reason which makes the Host–Kra characteristic factors powerful is their connection with nilsystems. The following is a slight generalization of [Reference Ziegler36, Theorem 3.7] (see [Reference Griesmer16, Lemma 4.4.3 and Theorem 4.10.1], or Proposition 3.1(ii) and [Reference Sun31, Theorem 3.7]), which is a higher dimensional version of the Host–Kra structure theorem [Reference Host and Kra18].
Theorem 3.5. Let
![]() $\mathbf {X}$
be an ergodic
$\mathbf {X}$
be an ergodic
![]() $\mathbb {Z}^{d}$
-system. Then
$\mathbb {Z}^{d}$
-system. Then
![]() $Z_{(\mathbb {Z}^{d})^{\times k}}(\mathbf {X})$
is an inverse limit of
$Z_{(\mathbb {Z}^{d})^{\times k}}(\mathbf {X})$
is an inverse limit of
![]() $(k-1)$
-step
$(k-1)$
-step
![]() $\mathbb {Z}^{d}$
-nilsystems.
$\mathbb {Z}^{d}$
-nilsystems.
3.2 Bessel’s inequality
An essential difference in the study of multiple ergodic averages between
![]() ${\mathbb Z}$
-systems and
${\mathbb Z}$
-systems and
![]() ${\mathbb Z}^{d}$
-systems is that in the former case, one can usually bound the average by some Host–Kra seminorm of a function f appearing in the average, whereas in the latter, one can only bound the averages by an average of a family of Host–Kra seminorms of f. To overcome this difficulty, inspired by the work of Tao and Ziegler [Reference Tao and Ziegler33], in this subsection, we derive an upper bound for expressions of the form
${\mathbb Z}^{d}$
-systems is that in the former case, one can usually bound the average by some Host–Kra seminorm of a function f appearing in the average, whereas in the latter, one can only bound the averages by an average of a family of Host–Kra seminorms of f. To overcome this difficulty, inspired by the work of Tao and Ziegler [Reference Tao and Ziegler33], in this subsection, we derive an upper bound for expressions of the form
![]() ${\overline {\mathbb {E}}}_{i\in I}\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H_{i,1},\ldots ,H_{i,s}}$
, where I is a finite set and
${\overline {\mathbb {E}}}_{i\in I}\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H_{i,1},\ldots ,H_{i,s}}$
, where I is a finite set and
![]() $H_{i,j}$
are subgroups of
$H_{i,j}$
are subgroups of
![]() ${\mathbb Z}^{d}$
.
${\mathbb Z}^{d}$
.
The proof of the following statement is similar to [Reference Tao and Ziegler33, Corollary 1.22].
Proposition 3.6. (Bessel’s inequality)
Let
![]() $t\in {\mathbb N}$
,
$t\in {\mathbb N}$
,
![]() $(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
$(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
![]() $\mathbb {Z}^{d}$
-system, I be a finite set of indices, and
$\mathbb {Z}^{d}$
-system, I be a finite set of indices, and
![]() $H_{i,j}, i\in I, 1\leq j\leq t$
be subgroups of
$H_{i,j}, i\in I, 1\leq j\leq t$
be subgroups of
![]() ${\mathbb Z}^{d}$
. Then for all
${\mathbb Z}^{d}$
. Then for all
![]() $f\in L^{\infty }(\mu )$
,
$f\in L^{\infty }(\mu )$
,
Proof. For convenience, let ![]() . Then,
. Then,
which, by the Cauchy–Schwarz inequality, is bounded by
By [Reference Tao and Ziegler33, Corollary 1.21],
![]() $L^{\infty }(Z_{H_{i,1},\ldots ,H_{i,t}})$
and
$L^{\infty }(Z_{H_{i,1},\ldots ,H_{i,t}})$
and
![]() $L^{\infty }(Z_{H_{j,1},\ldots ,H_{j,t}})$
are orthogonal on the orthogonal complement of
$L^{\infty }(Z_{H_{j,1},\ldots ,H_{j,t}})$
are orthogonal on the orthogonal complement of
![]() $L^{\infty }(Z_{\{H_{i,i'}+H_{j,j'}\}_{1\leq i',j'\leq t}})$
, and hence
$L^{\infty }(Z_{\{H_{i,i'}+H_{j,j'}\}_{1\leq i',j'\leq t}})$
, and hence
and we have the conclusion.
By repeatedly using Proposition 3.6, we have the following inequality.
Corollary 3.7. Let
![]() $t,s\in {\mathbb N}$
,
$t,s\in {\mathbb N}$
,
![]() $(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
$(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
![]() $\mathbb {Z}^{d}$
-system, I be a finite set of indices, and
$\mathbb {Z}^{d}$
-system, I be a finite set of indices, and
![]() $H_{i,j}, i\in I, 1\leq j\leq t,$
be subgroups of
$H_{i,j}, i\in I, 1\leq j\leq t,$
be subgroups of
![]() ${\mathbb Z}^{d}$
. Then for all
${\mathbb Z}^{d}$
. Then for all
![]() $f\in L^{\infty }(\mu )$
, we have
$f\in L^{\infty }(\mu )$
, we have
The next proposition provides an upper bound for
![]() $\mathbb {E}_{i\in I}\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H_{i,1},\ldots ,H_{i,t}}$
which can be combined with the previous two statements.
$\mathbb {E}_{i\in I}\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H_{i,1},\ldots ,H_{i,t}}$
which can be combined with the previous two statements.
Proposition 3.8. Let
![]() $t\in {\mathbb N}$
,
$t\in {\mathbb N}$
,
![]() $(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
$(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
![]() $\mathbb {Z}^{d}$
-system, I be a finite set of indices, and
$\mathbb {Z}^{d}$
-system, I be a finite set of indices, and
![]() $H_{i,j}, i\in I, 1\leq j\leq t$
be subgroups of
$H_{i,j}, i\in I, 1\leq j\leq t$
be subgroups of
![]() ${\mathbb Z}^{d}$
. Then, for all
${\mathbb Z}^{d}$
. Then, for all
![]() $f\in L^{\infty }(\mu )$
, with
$f\in L^{\infty }(\mu )$
, with
![]() $\Vert f\Vert _{L^{\infty }(\mu )}\leq 1$
,
$\Vert f\Vert _{L^{\infty }(\mu )}\leq 1$
,
Proof. Note that
Also, for all i, we have
 $$ \begin{align*} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}}&\leq \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f-\mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}})\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}} + \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert \mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}})\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}}\\ &= \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert \mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}})\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}}, \end{align*} $$
$$ \begin{align*} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}}&\leq \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f-\mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}})\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}} + \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert \mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}})\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}}\\ &= \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert \mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}})\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}}, \end{align*} $$
so
 $$ \begin{align} &\mathbb{E}_{i\in I}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}} \leq \mathbb{E}_{i\in I}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert \mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}}) \rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}} \nonumber\\ &\quad\leq \mathbb{E}_{i\in I}\Vert \mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}})\Vert_{2}^{1/2^{t-1}} \leq (\mathbb{E}_{i\in I}\Vert \mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}})\Vert^{2}_{2})^{1/2^{t}}, \end{align} $$
$$ \begin{align} &\mathbb{E}_{i\in I}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}} \leq \mathbb{E}_{i\in I}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert \mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}}) \rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{H_{i,1},\ldots,H_{i,t}} \nonumber\\ &\quad\leq \mathbb{E}_{i\in I}\Vert \mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}})\Vert_{2}^{1/2^{t-1}} \leq (\mathbb{E}_{i\in I}\Vert \mathbb{E}(f|Z_{H_{i,1},\ldots,H_{i,t}})\Vert^{2}_{2})^{1/2^{t}}, \end{align} $$
as was to be shown.
3.3 General properties of subgroups of
 ${\mathbb Z}^d$
and properties of polynomials
${\mathbb Z}^d$
and properties of polynomials
Recall that for a subset A of
![]() $\mathbb {Q}^{d}$
, we denote
$\mathbb {Q}^{d}$
, we denote
![]() $G(A):= \text {span}_{{\mathbb Q}} \{a\in A\}\cap {\mathbb Z}^{d}.$
Next, we summarize some properties of these sets.
$G(A):= \text {span}_{{\mathbb Q}} \{a\in A\}\cap {\mathbb Z}^{d}.$
Next, we summarize some properties of these sets.
Lemma 3.9. The following properties hold.
-
(i) For any set
 $A\subseteq {\mathbb Z}^d$
,
$A\subseteq {\mathbb Z}^d$
,
 $G(A)$
is a subgroup of
$G(A)$
is a subgroup of
 ${\mathbb Z}^d$
.
${\mathbb Z}^d$
. -
(ii) Let
 $A\subseteq \mathbb {Q}^d$
be a finite set and
$A\subseteq \mathbb {Q}^d$
be a finite set and
 $M(A)$
the matrix whose columns are the elements of A. Then
$M(A)$
the matrix whose columns are the elements of A. Then
 $G(A)=(M(A)\cdot {\mathbb Q}^{|A|})\cap {\mathbb Z}^d$
.
$G(A)=(M(A)\cdot {\mathbb Q}^{|A|})\cap {\mathbb Z}^d$
. -
(iii) If
 $H\subseteq {\mathbb Z}^d$
is the subgroup generated by
$H\subseteq {\mathbb Z}^d$
is the subgroup generated by
 $h_1,\ldots ,h_k\in {\mathbb Z}^d$
, then
$h_1,\ldots ,h_k\in {\mathbb Z}^d$
, then
 $G(H)=G(\{h_1,\ldots ,h_k\})$
. In particular, letting
$G(H)=G(\{h_1,\ldots ,h_k\})$
. In particular, letting
 $M(h_1,\ldots ,h_k)$
be the matrix whose columns are
$M(h_1,\ldots ,h_k)$
be the matrix whose columns are
 $h_1,\ldots ,h_k$
, we have that
$h_1,\ldots ,h_k$
, we have that
 $G(\langle h_1,\ldots ,h_k\rangle )=(M(h_1,\ldots ,h_k)\cdot {\mathbb Q}^{k}) \cap {\mathbb Z}^d$
.
$G(\langle h_1,\ldots ,h_k\rangle )=(M(h_1,\ldots ,h_k)\cdot {\mathbb Q}^{k}) \cap {\mathbb Z}^d$
. -
(iv) For any subgroup
 $H\subseteq {\mathbb Z}^d$
, H has finite index in
$H\subseteq {\mathbb Z}^d$
, H has finite index in
 $G(H)$
. Moreover,
$G(H)$
. Moreover,
 $G(H)$
is the largest subgroup of
$G(H)$
is the largest subgroup of
 ${\mathbb Z}^d$
which is a finite index extension of H.
${\mathbb Z}^d$
which is a finite index extension of H. -
(v) If not all of
 $a_1,\ldots ,a_k$
belong to a common proper subspace of
$a_1,\ldots ,a_k$
belong to a common proper subspace of
 ${\mathbb Q}^d$
, then
${\mathbb Q}^d$
, then
 $G(\{a_1,\ldots ,a_k\}) ={\mathbb Z}^d$
.
$G(\{a_1,\ldots ,a_k\}) ={\mathbb Z}^d$
.
Proof. Properties (i), (ii), and (iii) follow directly from the definitions.
To prove property (iv), let
![]() $\{g_1,\ldots ,g_k\}$
be a set such that
$\{g_1,\ldots ,g_k\}$
be a set such that
![]() $\langle g_1,\ldots ,g_k\rangle =G(H)$
. For each
$\langle g_1,\ldots ,g_k\rangle =G(H)$
. For each
![]() $i=1,\ldots ,k$
, there exist
$i=1,\ldots ,k$
, there exist
![]() $m_i$
and
$m_i$
and
![]() $h_i\in H$
such that
$h_i\in H$
such that
![]() $g_i={h_i}/{m_i}$
. The group
$g_i={h_i}/{m_i}$
. The group
![]() $\langle m_1g_1,\ldots ,m_kg_k\rangle $
is of finite index in
$\langle m_1g_1,\ldots ,m_kg_k\rangle $
is of finite index in
![]() $\langle g_1,\ldots ,g_k\rangle =G(H)$
and is contained in H. Therefore, H is of finite index in
$\langle g_1,\ldots ,g_k\rangle =G(H)$
and is contained in H. Therefore, H is of finite index in
![]() $G(H)$
.
$G(H)$
.
To see that
![]() $G(H)$
is the largest finite index extension of H, take
$G(H)$
is the largest finite index extension of H, take
![]() $H'$
to be any finite index extension of H and take
$H'$
to be any finite index extension of H and take
![]() $h'\in H'$
. Since
$h'\in H'$
. Since
![]() $H'$
is a finite index extension of H, we have that there exists
$H'$
is a finite index extension of H, we have that there exists
![]() $n\in {\mathbb N}$
such that
$n\in {\mathbb N}$
such that
![]() $nh'\in H$
. This implies that
$nh'\in H$
. This implies that
![]() $h'\in G(H)$
.
$h'\in G(H)$
.
To show property (v), reordering
![]() $a_1,\ldots ,a_k$
if needed, we may assume that
$a_1,\ldots ,a_k$
if needed, we may assume that
![]() $a_1,\ldots ,a_d$
are linearly independent vectors over
$a_1,\ldots ,a_d$
are linearly independent vectors over
![]() ${\mathbb Q}$
. It follows that
${\mathbb Q}$
. It follows that
![]() $\text {span}_{{\mathbb Q}}(\{a_1,\ldots ,a_d \})={\mathbb Q}^{d}$
and then
$\text {span}_{{\mathbb Q}}(\{a_1,\ldots ,a_d \})={\mathbb Q}^{d}$
and then
![]() $G(\{a_1,\ldots ,a_k\})\supseteq G(\{a_1,\ldots ,a_d\})={\mathbb Z}^d$
.
$G(\{a_1,\ldots ,a_k\})\supseteq G(\{a_1,\ldots ,a_d\})={\mathbb Z}^d$
.
Remark 3.10. If
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are subgroups of
$H_2$
are subgroups of
![]() ${\mathbb Z}^d$
, then
${\mathbb Z}^d$
, then
![]() $G(H_1)+G(H_2)\subseteq G(H_1+H_2)$
, with the inclusion possibly being strict. For instance, for
$G(H_1)+G(H_2)\subseteq G(H_1+H_2)$
, with the inclusion possibly being strict. For instance, for
![]() $H_1=\langle (1,2)\rangle $
,
$H_1=\langle (1,2)\rangle $
,
![]() $H_2=\langle (2,1) \rangle $
, we have that
$H_2=\langle (2,1) \rangle $
, we have that
![]() $G(H_1)=H_1$
,
$G(H_1)=H_1$
,
![]() $G(H_2)=H_2$
, and
$G(H_2)=H_2$
, and
![]() $H_1+H_2 \subsetneq G(H_1+H_2)={\mathbb Z}^2$
. Nevertheless, Lemma 3.9 implies that that
$H_1+H_2 \subsetneq G(H_1+H_2)={\mathbb Z}^2$
. Nevertheless, Lemma 3.9 implies that that
![]() $G(H_1)+G(H_2)$
has finite index in
$G(H_1)+G(H_2)$
has finite index in
![]() $G(H_1+H_2)$
.
$G(H_1+H_2)$
.
In the remainder of the section, we provide some algebraic lemmas that will be used later in the paper. For a set
![]() $E\subseteq {\mathbb Z}^d,$
we define its upper Banach density (or just upper density when there is no confusion) by
$E\subseteq {\mathbb Z}^d,$
we define its upper Banach density (or just upper density when there is no confusion) by ![]() If the limit exists, we say that its value is the Banach density (or just density) of E. The proof of the following lemma is routine (see also [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.11] for a more general version).
If the limit exists, we say that its value is the Banach density (or just density) of E. The proof of the following lemma is routine (see also [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.11] for a more general version).
Lemma 3.11. [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.11]
Let
![]() $\mathbf {c}\colon (\mathbb {Z}^{L})^{s}\to \mathbb {R}$
be a polynomial. Then either
$\mathbf {c}\colon (\mathbb {Z}^{L})^{s}\to \mathbb {R}$
be a polynomial. Then either
![]() $\mathbf {c}\equiv 0$
or the set of
$\mathbf {c}\equiv 0$
or the set of
![]() $\mathbf {h}\in (\mathbb {Z}^{L})^{s}$
such that
$\mathbf {h}\in (\mathbb {Z}^{L})^{s}$
such that
![]() ${\mathbf {c}}(\mathbf {h})=0$
is of (upper) Banach density
${\mathbf {c}}(\mathbf {h})=0$
is of (upper) Banach density
![]() $0$
.
$0$
.
Lemma 3.12. Let
![]() $v_{i}\in {\mathbb Z}^{L}, 1\leq i\leq k$
and U be a subset of
$v_{i}\in {\mathbb Z}^{L}, 1\leq i\leq k$
and U be a subset of
![]() ${\mathbb Z}^{k}$
of positive density. Then,
${\mathbb Z}^{k}$
of positive density. Then,
 $$ \begin{align} G\bigg(\bigg\{\sum_{1\leq i\leq k}h_{i} v_{i}\colon \mathbf{h}=(h_1,\ldots,h_k)\in U\bigg\}\bigg)=G(\{v_{i}\colon 1\leq i\leq k\}).\end{align} $$
$$ \begin{align} G\bigg(\bigg\{\sum_{1\leq i\leq k}h_{i} v_{i}\colon \mathbf{h}=(h_1,\ldots,h_k)\in U\bigg\}\bigg)=G(\{v_{i}\colon 1\leq i\leq k\}).\end{align} $$
Proof. Note that in equation (13), the right-hand side clearly includes the left-hand side. To prove the converse inclusion, it suffices to show that
Since U has positive density, it cannot be contained in any hyperplane of
![]() ${\mathbb Q}^k$
, so it must have at least k elements that are linearly independent over
${\mathbb Q}^k$
, so it must have at least k elements that are linearly independent over
![]() ${\mathbb Q}$
. Thus, equation (14) follows immediately.
${\mathbb Q}$
. Thus, equation (14) follows immediately.
Definition 3.13. Let
![]() $P\colon ({\mathbb Z}^{L})^D\to {\mathbb R}$
be a polynomial. Denote by
$P\colon ({\mathbb Z}^{L})^D\to {\mathbb R}$
be a polynomial. Denote by
![]() $\Delta P\colon ({\mathbb Z}^{L})^{D+1}\to {\mathbb R}$
the polynomial given by
$\Delta P\colon ({\mathbb Z}^{L})^{D+1}\to {\mathbb R}$
the polynomial given by ![]() for all
for all
![]() $n,h_{1},\ldots ,h_{D}\in {\mathbb Z}^{L}$
. For a polynomial
$n,h_{1},\ldots ,h_{D}\in {\mathbb Z}^{L}$
. For a polynomial
![]() $P\colon {\mathbb Z}^{L}\to {\mathbb R}$
, let
$P\colon {\mathbb Z}^{L}\to {\mathbb R}$
, let
![]() $\Delta ^0 P=P,$
and for
$\Delta ^0 P=P,$
and for
![]() $K>1, \Delta ^{K}P\colon ({\mathbb Z}^{L})^{D+K}\to \mathbb {R}$
is
$K>1, \Delta ^{K}P\colon ({\mathbb Z}^{L})^{D+K}\to \mathbb {R}$
is ![]() (where
(where
![]() $\Delta $
acts K times).
$\Delta $
acts K times).
Lemma 3.14. Let
![]() $K\in {\mathbb N}$
and
$K\in {\mathbb N}$
and
![]() $Q\colon {\mathbb Z}^{L}\to {\mathbb R}$
be a homogeneous polynomial with
$Q\colon {\mathbb Z}^{L}\to {\mathbb R}$
be a homogeneous polynomial with
![]() $\deg (Q)>K$
. If
$\deg (Q)>K$
. If
![]() $Q(n)\notin \mathbb {Q}[n]$
, then the set of
$Q(n)\notin \mathbb {Q}[n]$
, then the set of
![]() $(h_{1},\ldots ,h_{K})\in ({\mathbb Z}^{L})^{K}$
such that
$(h_{1},\ldots ,h_{K})\in ({\mathbb Z}^{L})^{K}$
such that
![]() $\Delta ^{K}Q(n,h_{1},\ldots ,h_{K})\notin \mathbb {Q}[n]$
is of density
$\Delta ^{K}Q(n,h_{1},\ldots ,h_{K})\notin \mathbb {Q}[n]$
is of density
![]() $1$
in
$1$
in
![]() $(\mathbb {Z}^{L})^{K}$
.
$(\mathbb {Z}^{L})^{K}$
.
Proof. We may write
![]() $Q(n)=\sum _{i=1}^{M}a_{i}Q_{i}(n)$
for some
$Q(n)=\sum _{i=1}^{M}a_{i}Q_{i}(n)$
for some
![]() $M\in {\mathbb N}$
, homogeneous polynomials
$M\in {\mathbb N}$
, homogeneous polynomials
![]() $Q_{1},\ldots ,Q_{M}$
in
$Q_{1},\ldots ,Q_{M}$
in
![]() ${\mathbb Q}[n]$
of degrees
${\mathbb Q}[n]$
of degrees
![]() $\deg (Q)$
, and real numbers
$\deg (Q)$
, and real numbers
![]() $a_{1},\ldots ,a_{M}\in {\mathbb R}$
which are linearly independent over
$a_{1},\ldots ,a_{M}\in {\mathbb R}$
which are linearly independent over
![]() ${\mathbb Q}$
(this can be done by taking
${\mathbb Q}$
(this can be done by taking
![]() $a_1\ldots ,a_M$
to be a basis of the
$a_1\ldots ,a_M$
to be a basis of the
![]() ${\mathbb Q}$
-span of the coefficients of Q). Since
${\mathbb Q}$
-span of the coefficients of Q). Since
![]() $Q(n)\notin \mathbb {Q}[n]$
, there exists some
$Q(n)\notin \mathbb {Q}[n]$
, there exists some
![]() ${1\leq i\leq M}$
such that
${1\leq i\leq M}$
such that
![]() $a_{i}\notin {\mathbb Q}$
and
$a_{i}\notin {\mathbb Q}$
and
![]() $Q_{i}\not \equiv 0$
. Without loss of generality, assume that
$Q_{i}\not \equiv 0$
. Without loss of generality, assume that
![]() $i=1.$
Since
$i=1.$
Since
![]() ${\deg (Q_{1})>K}$
, we have that
${\deg (Q_{1})>K}$
, we have that
![]() $\Delta ^{K}Q_{1}\not \equiv 0$
.
$\Delta ^{K}Q_{1}\not \equiv 0$
.
Suppose that
![]() $\Delta ^{K}Q(n,h_{1},\ldots ,h_{K})\kern1.3pt{\in}\kern1.3pt \mathbb {Q}[n]$
for some
$\Delta ^{K}Q(n,h_{1},\ldots ,h_{K})\kern1.3pt{\in}\kern1.3pt \mathbb {Q}[n]$
for some
![]() $(h_{1},\ldots ,h_{K})\kern1.3pt{\in}\kern1.3pt ({\mathbb Z}^{L})^{K}$
. Note that
$(h_{1},\ldots ,h_{K})\kern1.3pt{\in}\kern1.3pt ({\mathbb Z}^{L})^{K}$
. Note that
![]() $\Delta ^{K}Q(n,h_{1},\ldots ,h_{K})=\sum _{i=1}^{M}a_{i}\Delta ^{K}Q_{i}(n,h_{1},\ldots , h_{K})$
. Since each
$\Delta ^{K}Q(n,h_{1},\ldots ,h_{K})=\sum _{i=1}^{M}a_{i}\Delta ^{K}Q_{i}(n,h_{1},\ldots , h_{K})$
. Since each
![]() $\Delta ^{K}Q_{i}(n, h_{1},\ldots , h_{K})$
is a rational polynomial in terms of n of degree
$\Delta ^{K}Q_{i}(n, h_{1},\ldots , h_{K})$
is a rational polynomial in terms of n of degree
![]() $\deg (Q)-K$
and
$\deg (Q)-K$
and
![]() $a_{1},\ldots ,a_{M}\in {\mathbb R}$
are linearly independent over
$a_{1},\ldots ,a_{M}\in {\mathbb R}$
are linearly independent over
![]() ${\mathbb Q}$
, we must have that
${\mathbb Q}$
, we must have that
![]() $\Delta ^{K}Q_{1}(\cdot ,h_{1},\ldots ,h_{K})\equiv 0$
. So if the set of
$\Delta ^{K}Q_{1}(\cdot ,h_{1},\ldots ,h_{K})\equiv 0$
. So if the set of
![]() $(h_{1},\ldots ,h_{K})\in ({\mathbb Z}^{L})^{K}$
such that
$(h_{1},\ldots ,h_{K})\in ({\mathbb Z}^{L})^{K}$
such that
![]() $\Delta ^{K}Q(n,h_{1},\ldots ,h_{K})\in \mathbb {Q}[n]$
has positive density, then the set of
$\Delta ^{K}Q(n,h_{1},\ldots ,h_{K})\in \mathbb {Q}[n]$
has positive density, then the set of
![]() $(n,h_{1},\ldots ,h_{K})\in ({\mathbb Z}^{L})^{K+1}$
such that
$(n,h_{1},\ldots ,h_{K})\in ({\mathbb Z}^{L})^{K+1}$
such that
![]() $\Delta ^{K}Q_{1}(n,h_{1},\ldots ,h_{K})=0$
has positive density too. By [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.11],
$\Delta ^{K}Q_{1}(n,h_{1},\ldots ,h_{K})=0$
has positive density too. By [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.11],
![]() $\Delta ^{K}Q_{1}\equiv 0$
, which is a contradiction. This finishes the proof.
$\Delta ^{K}Q_{1}\equiv 0$
, which is a contradiction. This finishes the proof.
4 PET induction
In this section, we present the method we use to reduce the complexity of the polynomial iterates, that is, PET induction (PET is an abbreviation for ‘Polynomial Exhaustion Technique’), which was first introduced in [Reference Bergelson2]. To this end, we start by recalling a variation of van der Corput’s lemma from [Reference Donoso, Koutsogiannis and Sun7] that is convenient for our study. We then continue by presenting the inductive scheme via the use of van der Corput operations.
4.1 The van der Corput lemma
The standard tool used in reducing the complexity of polynomial families of iterates is van der Corput’s lemma (also known as ‘van der Corput’s trick’). We will use the following variation of it, the proof of which can be found in [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.2].
Lemma 4.1. (van der Corput lemma)
Let
![]() $(a(n;h_1,\ldots ,h_s))_{(n;h_1,\ldots ,h_s)\in ({\mathbb Z}^{L})^{s+1}}, s\in \mathbb {N}_0,$
be a sequence bounded by
$(a(n;h_1,\ldots ,h_s))_{(n;h_1,\ldots ,h_s)\in ({\mathbb Z}^{L})^{s+1}}, s\in \mathbb {N}_0,$
be a sequence bounded by
![]() $1$
in a Hilbert space
$1$
in a Hilbert space
![]() $\mathcal {H}$
. Then, for all
$\mathcal {H}$
. Then, for all
![]() $\tau \in \mathbb {N}_0$
,
$\tau \in \mathbb {N}_0$
,
 $$ \begin{align*} &\overline{\mathbb{E}}^{\square}_{h_1,\ldots,h_s\in {\mathbb Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \| \mathbb{E}_{n\in I_{N}} a(n;h_1,\ldots,h_s) \|^{2\tau}\\ &\,\leq\! 4^{\tau}\overline{\mathbb{E}}^{\square}_{h_1,\ldots,h_s,h_{s+1}\in {\mathbb Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\!\varlimsup_{N\to \infty} \kern-1pt\vert \mathbb{E}_{n\in I_{N}}\! \langle a(n+h_{s+1};h_1,\ldots,h_s) , a(n;h_1,\ldots,h_s) \rangle \vert^{\tau}\kern-1pt. \end{align*} $$
$$ \begin{align*} &\overline{\mathbb{E}}^{\square}_{h_1,\ldots,h_s\in {\mathbb Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \| \mathbb{E}_{n\in I_{N}} a(n;h_1,\ldots,h_s) \|^{2\tau}\\ &\,\leq\! 4^{\tau}\overline{\mathbb{E}}^{\square}_{h_1,\ldots,h_s,h_{s+1}\in {\mathbb Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\!\varlimsup_{N\to \infty} \kern-1pt\vert \mathbb{E}_{n\in I_{N}}\! \langle a(n+h_{s+1};h_1,\ldots,h_s) , a(n;h_1,\ldots,h_s) \rangle \vert^{\tau}\kern-1pt. \end{align*} $$
Remark 4.2. We use this unorthodox notation to separate the variable n from the
![]() $h_i$
terms. The variable n plays a different role in our study than the
$h_i$
terms. The variable n plays a different role in our study than the
![]() $h_i$
terms.
$h_i$
terms.
We also provide two applications of Lemma 4.1 for later use. The first one is to get an upper bound for single averages with polynomial iterates and a polynomial exponential weight. Let ![]() and recall Definition 3.13 for the polynomial
and recall Definition 3.13 for the polynomial
![]() $\Delta ^{K}P$
.
$\Delta ^{K}P$
.
Lemma 4.3. Let
![]() $P\colon {\mathbb Z}^{L}\to {\mathbb R}$
and
$P\colon {\mathbb Z}^{L}\to {\mathbb R}$
and
![]() $p\colon {\mathbb Z}^{L}\to {\mathbb Z}^{d}$
be polynomials. For all
$p\colon {\mathbb Z}^{L}\to {\mathbb Z}^{d}$
be polynomials. For all
![]() $K\in {\mathbb N}_0$
and
$K\in {\mathbb N}_0$
and
![]() $\tau \in {\mathbb N}$
, there exists
$\tau \in {\mathbb N}$
, there exists
![]() $C_{K,\tau }>0$
such that for every
$C_{K,\tau }>0$
such that for every
![]() $\mathbb {Z}^{d}$
-system,
$\mathbb {Z}^{d}$
-system,
![]() $(X,\mathcal {B},\mu , (T_{g})_{g\in \mathbb {Z}^{d}}),$
and
$(X,\mathcal {B},\mu , (T_{g})_{g\in \mathbb {Z}^{d}}),$
and
![]() ${f\in L^{\infty }(\mu )}$
bounded by 1, we have
${f\in L^{\infty }(\mu )}$
bounded by 1, we have
 $$ \begin{align*} &{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}}\exp(P(n))T_{p(n)}f\Vert_{2}^{2\tau} \\&\quad\leq C_{K,\tau}\overline{\mathbb{E}}^{\square}_{\mathbf{h}=(h_{1},\ldots,h_{K})\in({\mathbb Z}^{L})^{K}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}}\exp(\Delta^{K}P(n,\mathbf{h}))T_{\Delta^{K}p(n,\mathbf{h})}f\Vert^{\tau}_{2}. \end{align*} $$
$$ \begin{align*} &{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}}\exp(P(n))T_{p(n)}f\Vert_{2}^{2\tau} \\&\quad\leq C_{K,\tau}\overline{\mathbb{E}}^{\square}_{\mathbf{h}=(h_{1},\ldots,h_{K})\in({\mathbb Z}^{L})^{K}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}}\exp(\Delta^{K}P(n,\mathbf{h}))T_{\Delta^{K}p(n,\mathbf{h})}f\Vert^{\tau}_{2}. \end{align*} $$
Proof. When
![]() $K=0$
, there is nothing to prove. We now assume that the relation holds for some
$K=0$
, there is nothing to prove. We now assume that the relation holds for some
![]() $K\in {\mathbb N}_0$
and we show it for
$K\in {\mathbb N}_0$
and we show it for
![]() $K+1$
. Using Lemma 4.1 and the T-invariance of
$K+1$
. Using Lemma 4.1 and the T-invariance of
![]() $\mu $
, we get
$\mu $
, we get
 $$ \begin{align*} &\overline{\mathbb{E}}^{\square}_{\mathbf{h}=(h_1,\ldots,h_{K})\in ({\mathbb Z}^{L})^{K}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \| \mathbb{E}_{n\in I_{N}} \exp(\Delta^{K}P(n,\mathbf{h}))T_{\Delta^{K}p(n,\mathbf{h})}f \|^{2\tau}_{2}\\ &\;\kern-1pt\leq\! 4^{\kern-0.7pt\tau}\overline{\mathbb{E}}^{\square}_{\mathbf{h}=(h_1,\ldots,h_{K+1})\in ({\mathbb Z}^{L})^{K+1}}\kern-2pt{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\!\kern-2pt\varlimsup_{N\to \infty}\! \vert \mathbb{E}_{n\in I_{N}} \kern-2pt\!\int_{\kern-0.5pt X}\!\kern-1pt\exp(\Delta^{\kern-1.2pt K+1}\kern-1pt P(n,\mathbf{h})) T_{\kern-0.5pt \Delta^{\kern-0.5pt K+1}p(n,\mathbf{h})}f\!\cdot\! \overline{f}\,d\mu \vert^{\kern-1pt\tau} \\&\;\kern-1pt\leq 4^{\tau}\overline{\mathbb{E}}^{\square}_{\mathbf{h}=(h_1,\ldots,h_{K+1})\in ({\mathbb Z}^{L})^{K+1}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\!\varlimsup_{N\to \infty}\!\Vert \mathbb{E}_{n\in I_{N}} \exp(\Delta^{K+1}P(n,\mathbf{h}))T_{\Delta^{K+1}p(n,\mathbf{h})}f\Vert^{\tau}_{2}, \end{align*} $$
$$ \begin{align*} &\overline{\mathbb{E}}^{\square}_{\mathbf{h}=(h_1,\ldots,h_{K})\in ({\mathbb Z}^{L})^{K}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \| \mathbb{E}_{n\in I_{N}} \exp(\Delta^{K}P(n,\mathbf{h}))T_{\Delta^{K}p(n,\mathbf{h})}f \|^{2\tau}_{2}\\ &\;\kern-1pt\leq\! 4^{\kern-0.7pt\tau}\overline{\mathbb{E}}^{\square}_{\mathbf{h}=(h_1,\ldots,h_{K+1})\in ({\mathbb Z}^{L})^{K+1}}\kern-2pt{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\!\kern-2pt\varlimsup_{N\to \infty}\! \vert \mathbb{E}_{n\in I_{N}} \kern-2pt\!\int_{\kern-0.5pt X}\!\kern-1pt\exp(\Delta^{\kern-1.2pt K+1}\kern-1pt P(n,\mathbf{h})) T_{\kern-0.5pt \Delta^{\kern-0.5pt K+1}p(n,\mathbf{h})}f\!\cdot\! \overline{f}\,d\mu \vert^{\kern-1pt\tau} \\&\;\kern-1pt\leq 4^{\tau}\overline{\mathbb{E}}^{\square}_{\mathbf{h}=(h_1,\ldots,h_{K+1})\in ({\mathbb Z}^{L})^{K+1}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\!\varlimsup_{N\to \infty}\!\Vert \mathbb{E}_{n\in I_{N}} \exp(\Delta^{K+1}P(n,\mathbf{h}))T_{\Delta^{K+1}p(n,\mathbf{h})}f\Vert^{\tau}_{2}, \end{align*} $$
and hence the result (the constant that appears depends only on
![]() $\tau $
and K).
$\tau $
and K).
The second application of Lemma 4.1 provides an upper bound for single averages, with linear iterates and an exponential weight evaluated at a linear polynomial, on a product system. The proof is inspired by [Reference Donoso, Koutsogiannis and Sun7, Lemma 5.2] and [Reference Host and Kra19, Proposition 2.9].
Lemma 4.4. Let
![]() $(X,\mathcal {B},\mu )$
be a probability space,
$(X,\mathcal {B},\mu )$
be a probability space,
![]() $k,L\in {\mathbb N}$
and
$k,L\in {\mathbb N}$
and
![]() $T_{i,j}, 1\leq i\leq k, 1\leq j\leq L$
be commuting measure-preserving transformations on X. Denote
$T_{i,j}, 1\leq i\leq k, 1\leq j\leq L$
be commuting measure-preserving transformations on X. Denote
![]() $S_{j}=T_{1,j}\times \cdots \times T_{k,j}$
for
$S_{j}=T_{1,j}\times \cdots \times T_{k,j}$
for
![]() $1\leq j\leq L$
. Let
$1\leq j\leq L$
. Let
![]() $G_{i}$
be the group generated by
$G_{i}$
be the group generated by
![]() $T_{i,1},\ldots ,T_{i,L}$
. Then, for any polynomial
$T_{i,1},\ldots ,T_{i,L}$
. Then, for any polynomial
![]() $P\colon {\mathbb Z}^{L}\to {\mathbb R}$
of degree 1 and
$P\colon {\mathbb Z}^{L}\to {\mathbb R}$
of degree 1 and
![]() $f_{1},\ldots ,f_{k}\in L^{\infty }(\mu )$
bounded by 1, we have that
$f_{1},\ldots ,f_{k}\in L^{\infty }(\mu )$
bounded by 1, we have that
 $$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}}\exp(P(n))R_n f\Vert_{L^{2}(\mu^{\otimes k})}\leq 2\min_{1\leq i\leq k}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_{i}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{G_{i}^{\times 2}}, \end{align} $$
$$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}}\exp(P(n))R_n f\Vert_{L^{2}(\mu^{\otimes k})}\leq 2\min_{1\leq i\leq k}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_{i}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{G_{i}^{\times 2}}, \end{align} $$
where
![]() $f=f_{1}\otimes \cdots \otimes f_{k}$
and for
$f=f_{1}\otimes \cdots \otimes f_{k}$
and for ![]()
Proof. Fix
![]() $1\leq i\leq k$
and let
$1\leq i\leq k$
and let
![]() $P(n)=a\cdot n+b$
for some
$P(n)=a\cdot n+b$
for some
![]() $a\in {\mathbb R}^{L},b\in {\mathbb R}$
. Then, by Lemma 4.1 for
$a\in {\mathbb R}^{L},b\in {\mathbb R}$
. Then, by Lemma 4.1 for
![]() $\tau =2$
and
$\tau =2$
and
![]() $s=0$
, the fourth power of the left-hand side of equation (15) is bounded by
$s=0$
, the fourth power of the left-hand side of equation (15) is bounded by
 $$ \begin{align*} & 16\cdot\mathbb{E}^{\square}_{h\in{\mathbb Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\vert\int_{X^{k}}\mathbb{E}_{n\in I_{N}}\exp(P(n+h)-P(n))R_{n+h}f\cdot R_{n}\overline{f}\,d\mu^{\otimes k}\bigg\vert^{2} \\&\quad = 16\cdot\mathbb{E}^{\square}_{h\in{\mathbb Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\vert\int_{X^{k}}\mathbb{E}_{n\in I_{N}}\exp(a\cdot h)R_{h}f\cdot \overline{f}\,d\mu^{\otimes k}\bigg\vert^{2} \\&\quad = 16\cdot\mathbb{E}^{\square}_{h\in{\mathbb Z}^{L}}\bigg\vert\int_{X^{k}}R_{h}f\cdot \overline{f}\,d\mu^{\otimes k}\bigg\vert^{2} \\&\quad = 16\cdot\mathbb{E}^{\square}_{h=(h_{1},\ldots,h_{L})\in{\mathbb Z}^{L}}\bigg\vert\int_{X^{k}}\bigotimes_{i=1}^{k}\bigg((\prod_{j=1}^{L}T_{i,j}^{h_{j}})f_{i}\cdot \overline{f}_{i}\bigg)\,d\mu^{\otimes k}\bigg\vert^{2} \\&\quad \leq 16\cdot\mathbb{E}^{\square}_{h=(h_{1},\ldots,h_{L})\in{\mathbb Z}^{L}}\bigg\vert\int_{X}\bigg(\prod_{j=1}^{L}T_{i,j}^{h_{j}}\bigg) f_{i}\cdot \overline{f}_{i}\,d\mu\bigg\vert^{2} \\&\quad \leq 16\cdot\mathbb{E}^{\square}_{h=(h_{1},\ldots,h_{L})\in{\mathbb Z}^{L}}\bigg\vert\int_{X}\mathbb{E} \bigg((\prod_{j=1}^{L}T_{i,j}^{h_{j}})f_{i}\cdot \overline{f}_{i}\vert \mathcal{I}(G_{i})\bigg)\,d\mu\bigg\vert^{2} \\ &\quad =16\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_{i}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{4}_{G_{i}^{\times 2}}, \end{align*} $$
$$ \begin{align*} & 16\cdot\mathbb{E}^{\square}_{h\in{\mathbb Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\vert\int_{X^{k}}\mathbb{E}_{n\in I_{N}}\exp(P(n+h)-P(n))R_{n+h}f\cdot R_{n}\overline{f}\,d\mu^{\otimes k}\bigg\vert^{2} \\&\quad = 16\cdot\mathbb{E}^{\square}_{h\in{\mathbb Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\vert\int_{X^{k}}\mathbb{E}_{n\in I_{N}}\exp(a\cdot h)R_{h}f\cdot \overline{f}\,d\mu^{\otimes k}\bigg\vert^{2} \\&\quad = 16\cdot\mathbb{E}^{\square}_{h\in{\mathbb Z}^{L}}\bigg\vert\int_{X^{k}}R_{h}f\cdot \overline{f}\,d\mu^{\otimes k}\bigg\vert^{2} \\&\quad = 16\cdot\mathbb{E}^{\square}_{h=(h_{1},\ldots,h_{L})\in{\mathbb Z}^{L}}\bigg\vert\int_{X^{k}}\bigotimes_{i=1}^{k}\bigg((\prod_{j=1}^{L}T_{i,j}^{h_{j}})f_{i}\cdot \overline{f}_{i}\bigg)\,d\mu^{\otimes k}\bigg\vert^{2} \\&\quad \leq 16\cdot\mathbb{E}^{\square}_{h=(h_{1},\ldots,h_{L})\in{\mathbb Z}^{L}}\bigg\vert\int_{X}\bigg(\prod_{j=1}^{L}T_{i,j}^{h_{j}}\bigg) f_{i}\cdot \overline{f}_{i}\,d\mu\bigg\vert^{2} \\&\quad \leq 16\cdot\mathbb{E}^{\square}_{h=(h_{1},\ldots,h_{L})\in{\mathbb Z}^{L}}\bigg\vert\int_{X}\mathbb{E} \bigg((\prod_{j=1}^{L}T_{i,j}^{h_{j}})f_{i}\cdot \overline{f}_{i}\vert \mathcal{I}(G_{i})\bigg)\,d\mu\bigg\vert^{2} \\ &\quad =16\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_{i}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert^{4}_{G_{i}^{\times 2}}, \end{align*} $$
from where the result follows.
4.2 The van der Corput operation
To review the PET induction scheme, we will follow, and slightly modify, the approach from [Reference Donoso, Koutsogiannis and Sun7]. To this end, we extend the definitions that we have already given on the polynomial families of interest (see the beginning of §2.1), taking into account that we treat the first L-tuple of variables of the polynomials differently.
Before we list the steps of the van der Corput operation, we will present the manipulations of the inner product in Lemma 4.1 in a simple example where we have three essentially distinct polynomial iterates
![]() $(p_1(n),p_2(n),p_3(n))=(n^2,2n,n),$
to show how, by repeatedly running the van der Corput trick, we get an expression of linear iterates. This will be extended to general expressions in Theorem 4.9. Here, we want to study, for bounded by
$(p_1(n),p_2(n),p_3(n))=(n^2,2n,n),$
to show how, by repeatedly running the van der Corput trick, we get an expression of linear iterates. This will be extended to general expressions in Theorem 4.9. Here, we want to study, for bounded by
![]() $1$
functions
$1$
functions
![]() $f_1, f_2, f_3,$
the average of the sequence
$f_1, f_2, f_3,$
the average of the sequence
![]() $a(n)=T_1^{n^2}f_1\cdot T_2^{2n}f_2\cdot T_2^n f_3.$
Notice that we can write this sequence as a
$a(n)=T_1^{n^2}f_1\cdot T_2^{2n}f_2\cdot T_2^n f_3.$
Notice that we can write this sequence as a
![]() $\mathbb {Z}^2$
-action,
$\mathbb {Z}^2$
-action,
![]() $a(n)=T_{(n^2,0)}f_1\cdot T_{(0,2n)}f_2\cdot T_{(0,n)}f_3$
for the triple of polynomials
$a(n)=T_{(n^2,0)}f_1\cdot T_{(0,2n)}f_2\cdot T_{(0,n)}f_3$
for the triple of polynomials
![]() $((n^2,0),(0,2n),(0,n)).$
Using Lemma 4.1, we have
$((n^2,0),(0,2n),(0,n)).$
Using Lemma 4.1, we have
 $$ \begin{align*} &{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \| \mathbb{E}_{n\in I_{N}} a(n) \|^{2} \\ &\quad \leq 4\overline{\mathbb{E}}^{\square}_{h_1\in {\mathbb Z}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \vert \mathbb{E}_{n\in I_{N}} \langle a(n+h_{1}) , a(n) \rangle \vert\\ &\quad = 4\overline{\mathbb{E}}^{\square}_{h_1\in {\mathbb Z}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \vert \mathbb{E}_{n\in I_{N}}\int_X T_1^{(n+h_1)^2}f_1\cdot T_2^{2(n+h_1)}f_2\cdot T_2^{n+h_1}f_3\cdot T_1^{n^2}\bar{f}_1\\ &\qquad\times T_2^{2n}\bar{f}_2 \cdot T_2^{n}\bar{f}_3 \,d\mu\vert. \end{align*} $$
$$ \begin{align*} &{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \| \mathbb{E}_{n\in I_{N}} a(n) \|^{2} \\ &\quad \leq 4\overline{\mathbb{E}}^{\square}_{h_1\in {\mathbb Z}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \vert \mathbb{E}_{n\in I_{N}} \langle a(n+h_{1}) , a(n) \rangle \vert\\ &\quad = 4\overline{\mathbb{E}}^{\square}_{h_1\in {\mathbb Z}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \vert \mathbb{E}_{n\in I_{N}}\int_X T_1^{(n+h_1)^2}f_1\cdot T_2^{2(n+h_1)}f_2\cdot T_2^{n+h_1}f_3\cdot T_1^{n^2}\bar{f}_1\\ &\qquad\times T_2^{2n}\bar{f}_2 \cdot T_2^{n}\bar{f}_3 \,d\mu\vert. \end{align*} $$
Using the fact that
![]() $T_2$
is measure-preserving, we compose by
$T_2$
is measure-preserving, we compose by
![]() $T_2^{-n}$
(notice that n is the polynomial of the minimum degree in the expression) to get
$T_2^{-n}$
(notice that n is the polynomial of the minimum degree in the expression) to get
 $$ \begin{align*} & 4\overline{\mathbb{E}}^{\square}_{h_1\in {\mathbb Z}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \Bigg \vert \mathbb{E}_{n\in I_{N}}\int_X \bar{f}_3\cdot T_2^{h_1}f_3\cdot T_1^{n^2+2h_1 n}T_2^{-n}(T_1^{h_1^2}f_1)\\ &\quad \times T_1^{n^2}T_2^{-n}\bar{f}_1\cdot T_2^{n}(T_2^{2h_1}f_2\cdot \bar{f}_2)\;d\mu\Bigg\vert, \end{align*} $$
$$ \begin{align*} & 4\overline{\mathbb{E}}^{\square}_{h_1\in {\mathbb Z}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \Bigg \vert \mathbb{E}_{n\in I_{N}}\int_X \bar{f}_3\cdot T_2^{h_1}f_3\cdot T_1^{n^2+2h_1 n}T_2^{-n}(T_1^{h_1^2}f_1)\\ &\quad \times T_1^{n^2}T_2^{-n}\bar{f}_1\cdot T_2^{n}(T_2^{2h_1}f_2\cdot \bar{f}_2)\;d\mu\Bigg\vert, \end{align*} $$
where we grouped the functions with the same linear terms.
Using the Cauchy–Schwarz inequality (to discard the terms that have iterates independent of n), the previous relation is bounded by
 $$ \begin{align*}\overline{\mathbb{E}}^{\square}_{h_1\in {\mathbb Z}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \| \mathbb{E}_{n\in I_{N}}T_1^{n^2+2h_1 n}T_2^{-n}(T_1^{h_1^2}f_1)\cdot T_1^{n^2}T_2^{-n}\bar{f}_1\cdot T_2^{n}(T_2^{2h_1}f_2\cdot \bar{f}_2)\|.\end{align*} $$
$$ \begin{align*}\overline{\mathbb{E}}^{\square}_{h_1\in {\mathbb Z}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \| \mathbb{E}_{n\in I_{N}}T_1^{n^2+2h_1 n}T_2^{-n}(T_1^{h_1^2}f_1)\cdot T_1^{n^2}T_2^{-n}\bar{f}_1\cdot T_2^{n}(T_2^{2h_1}f_2\cdot \bar{f}_2)\|.\end{align*} $$
Exactly because of the grouping of the terms of the same linear iterates, the resulting polynomial iterates,
![]() $(n^2+2h_1 n,-n), (n^2,-n), (0,n),$
have the property that they are non-constant and that their pairwise differences are non-constant (this will lead us below to the notion of the ‘essentially distinct’ vector-valued polynomials).
$(n^2+2h_1 n,-n), (n^2,-n), (0,n),$
have the property that they are non-constant and that their pairwise differences are non-constant (this will lead us below to the notion of the ‘essentially distinct’ vector-valued polynomials).
Similarly, skipping the details, using Lemma 4.1, composing with
![]() $T_2^{-n}$
(the polynomial
$T_2^{-n}$
(the polynomial
![]() $(0,n)$
is of minimum ‘degree’—see below for the definition of the degree of a vector-valued polynomial), the square of the previous quantity can be bounded by
$(0,n)$
is of minimum ‘degree’—see below for the definition of the degree of a vector-valued polynomial), the square of the previous quantity can be bounded by
 $$ \begin{align*} & \overline{\mathbb{E}}^{\square}_{(h_{1},h_2)\in {\mathbb Z}^{2}}\!{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\!\kern-1pt\varlimsup_{N\to \infty}\!\| \mathbb{E}_{n\in I_{N}}\!T_1^{n^2+2(h_1+h_2)n}T_2^{-2n}(T_1^{(h_1+h_2)^2}\!T_2^{-h_2}f_1)\! \cdot T_1^{n^2+2h_1n} T_2^{-2n}(T_1^{h_1^2}\bar{f}_1) \\ & \quad\times T_1^{n^2+2h_2n}T_2^{-2n}(T_1^{h_2^2}T_2^{-h_2}\bar{f}_1) \cdot T_1^{n^2}T_2^{-2n}f_1 \|. \end{align*} $$
$$ \begin{align*} & \overline{\mathbb{E}}^{\square}_{(h_{1},h_2)\in {\mathbb Z}^{2}}\!{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\!\kern-1pt\varlimsup_{N\to \infty}\!\| \mathbb{E}_{n\in I_{N}}\!T_1^{n^2+2(h_1+h_2)n}T_2^{-2n}(T_1^{(h_1+h_2)^2}\!T_2^{-h_2}f_1)\! \cdot T_1^{n^2+2h_1n} T_2^{-2n}(T_1^{h_1^2}\bar{f}_1) \\ & \quad\times T_1^{n^2+2h_2n}T_2^{-2n}(T_1^{h_2^2}T_2^{-h_2}\bar{f}_1) \cdot T_1^{n^2}T_2^{-2n}f_1 \|. \end{align*} $$
Note that the iterates in the previous relation are ‘essentially distinct’ for ‘almost all’ tuples
![]() $(h_{1},h_{2})\in \mathbb {Z}^{2}$
.
$(h_{1},h_{2})\in \mathbb {Z}^{2}$
.
Analogously, using Lemma 4.1 once more, noticing that all the resulting terms in the expression will have the factor
![]() $T_1^{n^2}T_2^{-2n},$
where
$T_1^{n^2}T_2^{-2n},$
where
![]() $(n^2,-2n)$
is the polynomial of minimum ‘degree’, we can bound, composing with the term
$(n^2,-2n)$
is the polynomial of minimum ‘degree’, we can bound, composing with the term
![]() $T_1^{-n^2}T_2^{2n}$
, the square of the previous relation by
$T_1^{-n^2}T_2^{2n}$
, the square of the previous relation by
 $$ \begin{align*} & \overline{\mathbb{E}}^{\square}_{(h_{1},h_2,h_{3})\in {\mathbb Z}^{3}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\| \mathbb{E}_{n\in I_{N}} T_1^{2(h_1+h_2+h_3)n}(T_1^{(h_1+h_2+h_3)^2}T_2^{-h_2-2h_3}f_1)\\ &\quad \times T_1^{2(h_2+h_3)n}(T_1^{(h_2+h_3)^2}T_2^{-h_2-2h_3}\bar{f}_1)\cdot T_1^{2(h_1+h_3)n}(T_1^{(h_1+h_3)^2}T_2^{-2h_3}\bar{f}_1) \cdot T_1^{2h_3 n}(T_1^{h_3^2}T_2^{-2h_3}f_1) \\ &\quad \times T_1^{2(h_1+h_2)n}(T_1^{(h_1+h_2)^2}T_2^{-h_2}\bar{f}_1) \cdot T_1^{2h_2 n}(T_1^{h_2^2}T_2^{-h_2}f_1) \cdot T_1^{2h_1 n}(T_1^{h_1^2}f_1)\;d\mu\|. \end{align*} $$
$$ \begin{align*} & \overline{\mathbb{E}}^{\square}_{(h_{1},h_2,h_{3})\in {\mathbb Z}^{3}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\| \mathbb{E}_{n\in I_{N}} T_1^{2(h_1+h_2+h_3)n}(T_1^{(h_1+h_2+h_3)^2}T_2^{-h_2-2h_3}f_1)\\ &\quad \times T_1^{2(h_2+h_3)n}(T_1^{(h_2+h_3)^2}T_2^{-h_2-2h_3}\bar{f}_1)\cdot T_1^{2(h_1+h_3)n}(T_1^{(h_1+h_3)^2}T_2^{-2h_3}\bar{f}_1) \cdot T_1^{2h_3 n}(T_1^{h_3^2}T_2^{-2h_3}f_1) \\ &\quad \times T_1^{2(h_1+h_2)n}(T_1^{(h_1+h_2)^2}T_2^{-h_2}\bar{f}_1) \cdot T_1^{2h_2 n}(T_1^{h_2^2}T_2^{-h_2}f_1) \cdot T_1^{2h_1 n}(T_1^{h_1^2}f_1)\;d\mu\|. \end{align*} $$
The iterates in this last relation are linear with distinct coefficients for ‘almost all’ tuples
![]() $(h_{1},h_{2},h_{3})\in \mathbb {Z}^{3}$
. So, the eighth power of the initial expression is bounded by the previous relation.
$(h_{1},h_{2},h_{3})\in \mathbb {Z}^{3}$
. So, the eighth power of the initial expression is bounded by the previous relation.
The previous example leads naturally to the following notions.
Definition 4.5. For a polynomial
![]() $p(n;h_{1},\ldots ,h_{s})\colon (\mathbb {Z}^{L})^{s+1}\to \mathbb {Z}$
, we denote by
$p(n;h_{1},\ldots ,h_{s})\colon (\mathbb {Z}^{L})^{s+1}\to \mathbb {Z}$
, we denote by
![]() $\deg (p)$
the degree of p with respect to n (for example, for
$\deg (p)$
the degree of p with respect to n (for example, for
![]() $s=1, L=2$
, the degree of
$s=1, L=2$
, the degree of
![]() $p(n_{1},n_{2};h_{1,1},h_{1,2})=h_{1,1}h_{1,2}n_{1}^{2}+h_{1,1}^{5}n_{2}$
is 2).
$p(n_{1},n_{2};h_{1,1},h_{1,2})=h_{1,1}h_{1,2}n_{1}^{2}+h_{1,1}^{5}n_{2}$
is 2).
For a polynomial
![]() $p(n;h_{1},\ldots ,h_{s})=(p_{1}(n;h_{1},\ldots ,h_{s}),\ldots ,p_{d}(n;h_{1},\ldots ,h_{s}))\colon (\mathbb {Z}^{L})^{s+1}\to \mathbb {Z}^{d},$
we let
$p(n;h_{1},\ldots ,h_{s})=(p_{1}(n;h_{1},\ldots ,h_{s}),\ldots ,p_{d}(n;h_{1},\ldots ,h_{s}))\colon (\mathbb {Z}^{L})^{s+1}\to \mathbb {Z}^{d},$
we let
![]() $\deg (p)=\max _{1\leq i\leq d}\deg (p_{i})$
and we say that p is non-constant if
$\deg (p)=\max _{1\leq i\leq d}\deg (p_{i})$
and we say that p is non-constant if
![]() $\deg (p)>0$
(that is, some
$\deg (p)>0$
(that is, some
![]() $p_i$
is a non-constant function of n), otherwise, we say that p is constant. The polynomials
$p_i$
is a non-constant function of n), otherwise, we say that p is constant. The polynomials
![]() $q_{1},\ldots ,q_{k}\colon (\mathbb {Z}^{L})^{s+1}\to \mathbb {Z}^{d}$
are called essentially distinct if they are non-constant and
$q_{1},\ldots ,q_{k}\colon (\mathbb {Z}^{L})^{s+1}\to \mathbb {Z}^{d}$
are called essentially distinct if they are non-constant and
![]() $q_i-q_j$
is non-constant for all
$q_i-q_j$
is non-constant for all
![]() $i\neq j$
. Finally, for a tuple
$i\neq j$
. Finally, for a tuple
![]() $\mathbf {q}=(q_{1},\ldots ,q_{k}),$
we let
$\mathbf {q}=(q_{1},\ldots ,q_{k}),$
we let
![]() $\deg (\mathbf {q})=\max _{1\leq i\leq k}\deg (q_{i}).$
(For clarity, we use non-bold letters for vectors (of polynomials) and bold letters for vectors of vectors (of polynomials).)
$\deg (\mathbf {q})=\max _{1\leq i\leq k}\deg (q_{i}).$
(For clarity, we use non-bold letters for vectors (of polynomials) and bold letters for vectors of vectors (of polynomials).)
Let
![]() $(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
$(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
![]() $\mathbb {Z}^{d}$
-system,
$\mathbb {Z}^{d}$
-system,
![]() $q_{1},\ldots ,q_{k}\colon (\mathbb {Z}^{L})^{s+1}\to \mathbb {Z}^{d}$
be polynomials, and
$q_{1},\ldots ,q_{k}\colon (\mathbb {Z}^{L})^{s+1}\to \mathbb {Z}^{d}$
be polynomials, and
![]() $g_{1},\ldots , g_{k}\colon X\times (\mathbb {Z}^{L})^{s}\to \mathbb {R}$
be functions such that
$g_{1},\ldots , g_{k}\colon X\times (\mathbb {Z}^{L})^{s}\to \mathbb {R}$
be functions such that
![]() $g_{m}(\cdot ;h_{1},\ldots ,h_{s})$
is an
$g_{m}(\cdot ;h_{1},\ldots ,h_{s})$
is an
![]() $L^{\infty }(\mu )$
function bounded by
$L^{\infty }(\mu )$
function bounded by
![]() $1$
for all
$1$
for all
![]() $h_{1},\ldots ,h_{s}\in \mathbb {Z}^L, 1\leq m\leq k$
. If
$h_{1},\ldots ,h_{s}\in \mathbb {Z}^L, 1\leq m\leq k$
. If
![]() $\mathbf {q}=(q_{1},\ldots ,q_{k})$
and
$\mathbf {q}=(q_{1},\ldots ,q_{k})$
and
![]() $\mathbf {g}=(g_{1},\ldots ,g_{k}),$
we say that
$\mathbf {g}=(g_{1},\ldots ,g_{k}),$
we say that
![]() $A=(L,s,k,\mathbf {g},\mathbf {q})$
is a PET-tuple, and for
$A=(L,s,k,\mathbf {g},\mathbf {q})$
is a PET-tuple, and for
![]() $\tau \in {\mathbb N}_0$
, we set
$\tau \in {\mathbb N}_0$
, we set

We define
![]() $\deg (A)=\deg (\mathbf {q})$
, and say that A is non-degenerate if
$\deg (A)=\deg (\mathbf {q})$
, and say that A is non-degenerate if
![]() $\mathbf {q}$
is a family of essentially distinct polynomials (for convenience,
$\mathbf {q}$
is a family of essentially distinct polynomials (for convenience,
![]() $\mathbf {q}$
will be called non-degenerate as well). For
$\mathbf {q}$
will be called non-degenerate as well). For
![]() $1\leq m\leq k$
, the tuple A is m-standard for
$1\leq m\leq k$
, the tuple A is m-standard for
![]() $f\in L^\infty (\mu )$
if
$f\in L^\infty (\mu )$
if
![]() $\deg (A)=\deg (q_{m})$
and
$\deg (A)=\deg (q_{m})$
and
![]() $g_{m}(x;h_{1},\ldots ,h_{s})=f(x)$
for every
$g_{m}(x;h_{1},\ldots ,h_{s})=f(x)$
for every
![]() $x,h_1,\ldots ,h_s$
. That is, f is the mth function in
$x,h_1,\ldots ,h_s$
. That is, f is the mth function in
![]() $\mathbf {g}$
, only depending on the first variable, and the polynomial
$\mathbf {g}$
, only depending on the first variable, and the polynomial
![]() $q_m$
that acts on f is of the highest degree. (Here, we say m-standard for f to highlight the function of interest as, after running the vdC-operation, the position of the functions in the expression we deal with changes.) The tuple A will be called semi-standard for f if there exists
$q_m$
that acts on f is of the highest degree. (Here, we say m-standard for f to highlight the function of interest as, after running the vdC-operation, the position of the functions in the expression we deal with changes.) The tuple A will be called semi-standard for f if there exists
![]() $1\leq m\leq k$
such that
$1\leq m\leq k$
such that
![]() $g_{m}(x;h_{1},\ldots ,h_{s})=f(x)$
for every
$g_{m}(x;h_{1},\ldots ,h_{s})=f(x)$
for every
![]() $x,h_1,\ldots ,h_s$
. In this case, we do not require the function f to have a specific position in
$x,h_1,\ldots ,h_s$
. In this case, we do not require the function f to have a specific position in
![]() $\mathbf {g}$
nor that the polynomial acting on f be of the highest degree.
$\mathbf {g}$
nor that the polynomial acting on f be of the highest degree.
As an example, for a
![]() $\mathbb {Z}$
-system
$\mathbb {Z}$
-system
![]() $(X,\mathcal {B},\mu ,T),$
take
$(X,\mathcal {B},\mu ,T),$
take
![]() $L=s=1, k=3, q_1(n,h)=n^3, q_2(n,h)=3n^2h, q_3(n,h)=3nh^2,$
and, for
$L=s=1, k=3, q_1(n,h)=n^3, q_2(n,h)=3n^2h, q_3(n,h)=3nh^2,$
and, for
![]() $f,g\in L^\infty (\mu ),$
let
$f,g\in L^\infty (\mu ),$
let
![]() $g_1(x,h)=f(x), g_2(x,h)=g(x),$
and
$g_1(x,h)=f(x), g_2(x,h)=g(x),$
and
![]() $g_3(x,h)=T^{h^3}f(x).$
$g_3(x,h)=T^{h^3}f(x).$
Then, we have that A is 1-standard for
![]() $f,$
semi-standard for f and
$f,$
semi-standard for f and
![]() $g,$
and, for
$g,$
and, for
![]() $\kappa \in \mathbb {N}_0$
,
$\kappa \in \mathbb {N}_0$
,

For each non-degenerate PET-tuple
![]() $A{\kern-1pt}={\kern-1.5pt}(L,{\kern-0.5pt}s,{\kern-0.5pt}k,{\kern-0.5pt}\mathbf {g},{\kern-0.5pt}\mathbf {q})$
and polynomial
$A{\kern-1pt}={\kern-1.5pt}(L,{\kern-0.5pt}s,{\kern-0.5pt}k,{\kern-0.5pt}\mathbf {g},{\kern-0.5pt}\mathbf {q})$
and polynomial
![]() $q\colon{\kern-1.2pt} (\mathbb {Z}^{L})^{s+1}{\kern-1.2pt}\to{\kern-1.2pt} \mathbb {Z}^{d}$
, we define the vdC-operation,
$q\colon{\kern-1.2pt} (\mathbb {Z}^{L})^{s+1}{\kern-1.2pt}\to{\kern-1.2pt} \mathbb {Z}^{d}$
, we define the vdC-operation,
![]() $\partial _{q}A$
, according to the following three steps. (Actually, the vdC-operation can be defined for any PET-tuple, not just for non-degenerate ones. Similarly, being a procedure that reduces complexity, PET induction can be applied to any family of polynomials. As the expressions of interest in this paper correspond to non-degenerate tuples, we consider only this case.)
$\partial _{q}A$
, according to the following three steps. (Actually, the vdC-operation can be defined for any PET-tuple, not just for non-degenerate ones. Similarly, being a procedure that reduces complexity, PET induction can be applied to any family of polynomials. As the expressions of interest in this paper correspond to non-degenerate tuples, we consider only this case.)
Step 1: For all
![]() $1\leq m\leq k$
, let
$1\leq m\leq k$
, let
![]() $g^{\ast }_{m}=g^{\ast }_{m+k}=g_{m},$
and
$g^{\ast }_{m}=g^{\ast }_{m+k}=g_{m},$
and
![]() $q^{\ast }_1,\ldots ,q^{\ast }_{2k} \colon (\mathbb {Z}^{L})^{s+2}\to \mathbb {Z}^{d}$
be the polynomials defined as
$q^{\ast }_1,\ldots ,q^{\ast }_{2k} \colon (\mathbb {Z}^{L})^{s+2}\to \mathbb {Z}^{d}$
be the polynomials defined as
 $$ \begin{align*}\displaystyle q^{\ast}_m(n;h_1,\ldots,h_{s+1})=\left\{\!\begin{array}{ll} q_m(n+h_{s+1};h_1,\ldots,h_{s})-q(n;h_1,\ldots,h_{s}), & 1\leq m\leq k,\\ q_{m-k}(n;h_1,\ldots,h_{s})\!-\!q(n;h_1,\ldots,h_{s}), & k\!+\!1\!\leq\! m\!\leq\! 2k,\end{array} \right. \end{align*} $$
$$ \begin{align*}\displaystyle q^{\ast}_m(n;h_1,\ldots,h_{s+1})=\left\{\!\begin{array}{ll} q_m(n+h_{s+1};h_1,\ldots,h_{s})-q(n;h_1,\ldots,h_{s}), & 1\leq m\leq k,\\ q_{m-k}(n;h_1,\ldots,h_{s})\!-\!q(n;h_1,\ldots,h_{s}), & k\!+\!1\!\leq\! m\!\leq\! 2k,\end{array} \right. \end{align*} $$
that is, we subtract the polynomial q from the first k polynomials after we have shifted by
![]() $h_{s+1}$
the first L variables, and for the second k ones, we subtract q. (In practice, this q will be one of the
$h_{s+1}$
the first L variables, and for the second k ones, we subtract q. (In practice, this q will be one of the
![]() $q_i$
terms of minimum degree.) Denote
$q_i$
terms of minimum degree.) Denote
![]() $\mathbf {q}^{\ast }=(q^{\ast }_{1},\ldots ,q^{\ast }_{2k})$
.
$\mathbf {q}^{\ast }=(q^{\ast }_{1},\ldots ,q^{\ast }_{2k})$
.
Step 2: We remove from
![]() $q^{\ast }_{1},\ldots ,q^{\ast }_{2k}$
the polynomials which are constant and the associated functions
$q^{\ast }_{1},\ldots ,q^{\ast }_{2k}$
the polynomials which are constant and the associated functions
![]() $g_i^\ast $
in the expression (we group all these terms together and we see the resulting term as a single constant one, in terms of n). As we already saw in the example at the beginning of this subsection, this is justified via the use of the Cauchy–Schwarz inequality and the fact that the functions
$g_i^\ast $
in the expression (we group all these terms together and we see the resulting term as a single constant one, in terms of n). As we already saw in the example at the beginning of this subsection, this is justified via the use of the Cauchy–Schwarz inequality and the fact that the functions
![]() $g_m$
are bounded. Then we put the non-constant ones in groups
$g_m$
are bounded. Then we put the non-constant ones in groups
![]() $J_{i}=\{\tilde {q}_{i,1},\ldots ,\tilde {q}_{i,t_{i}}\}, 1\leq i\leq k'$
for some
$J_{i}=\{\tilde {q}_{i,1},\ldots ,\tilde {q}_{i,t_{i}}\}, 1\leq i\leq k'$
for some
![]() $k', t_{i}\in \mathbb {N}$
such that any two polynomials are essentially distinct if and only if they belong to different groups. Next, we write
$k', t_{i}\in \mathbb {N}$
such that any two polynomials are essentially distinct if and only if they belong to different groups. Next, we write
![]() $\tilde {q}_{i,j}(n;h_{1},\ldots ,h_{s+1})=\tilde {q}_{i,1}(n;h_{1},\ldots ,h_{s+1})+\tilde {p}_{i,j}(h_{1},\ldots ,h_{s+1})$
for some polynomial
$\tilde {q}_{i,j}(n;h_{1},\ldots ,h_{s+1})=\tilde {q}_{i,1}(n;h_{1},\ldots ,h_{s+1})+\tilde {p}_{i,j}(h_{1},\ldots ,h_{s+1})$
for some polynomial
![]() $\tilde {p}_{i,j}$
for all
$\tilde {p}_{i,j}$
for all
![]() $1\leq j\leq t_{i}, 1\leq i\leq k'$
. For convenience, we also relabel what remains, as some of the initial terms may have been removed because of the grouping of the polynomials, of the
$1\leq j\leq t_{i}, 1\leq i\leq k'$
. For convenience, we also relabel what remains, as some of the initial terms may have been removed because of the grouping of the polynomials, of the
![]() $g^{\ast }_{1},\ldots , g^{\ast }_{2k}$
accordingly as
$g^{\ast }_{1},\ldots , g^{\ast }_{2k}$
accordingly as
![]() $\tilde {g}_{i,j}$
for all
$\tilde {g}_{i,j}$
for all
![]() $1\leq j\leq t_{i}, 1\leq i\leq k'$
.
$1\leq j\leq t_{i}, 1\leq i\leq k'$
.
Step 3: For all
![]() $1\leq i\leq k'$
, let
$1\leq i\leq k'$
, let
![]() $q^{\prime}_{i}=\tilde {q}_{i,1}$
and
$q^{\prime}_{i}=\tilde {q}_{i,1}$
and
 $$ \begin{align*}g^{\prime}_{i}(x;h_{1},\ldots,h_{s+1})=\tilde{g}_{i,1}(x;h_{1},\ldots,h_{s+1})\prod^{t_{i}}_{j=2}T_{\tilde{p}_{i,j}(h_{1},\ldots,h_{s+1})}\tilde{g}_{i,j}(x;h_{1},\ldots,h_{s+1}).\end{align*} $$
$$ \begin{align*}g^{\prime}_{i}(x;h_{1},\ldots,h_{s+1})=\tilde{g}_{i,1}(x;h_{1},\ldots,h_{s+1})\prod^{t_{i}}_{j=2}T_{\tilde{p}_{i,j}(h_{1},\ldots,h_{s+1})}\tilde{g}_{i,j}(x;h_{1},\ldots,h_{s+1}).\end{align*} $$
We set
![]() $\mathbf {q}'=(q^{\prime}_{1},\ldots ,q^{\prime}_{k'})$
,
$\mathbf {q}'=(q^{\prime}_{1},\ldots ,q^{\prime}_{k'})$
,
![]() $\mathbf {g}'=(g^{\prime}_{1},\ldots ,g^{\prime}_{k'})$
and we denote the new PET-tuple by
$\mathbf {g}'=(g^{\prime}_{1},\ldots ,g^{\prime}_{k'})$
and we denote the new PET-tuple by ![]() . (Here we abuse the notation by writing
. (Here we abuse the notation by writing
![]() $\partial _{q}A$
to denote any such tuple, obtained from Steps 1 to 3. Strictly speaking,
$\partial _{q}A$
to denote any such tuple, obtained from Steps 1 to 3. Strictly speaking,
![]() $\partial _{q}A$
is not uniquely defined as the order of the grouping of
$\partial _{q}A$
is not uniquely defined as the order of the grouping of
![]() $q^{\prime}_{1},\ldots ,q^{\prime}_{2k}$
in Step 2 is ambiguous. However, this is done without loss of generality, since the order does not affect the value of
$q^{\prime}_{1},\ldots ,q^{\prime}_{2k}$
in Step 2 is ambiguous. However, this is done without loss of generality, since the order does not affect the value of
![]() $S(\partial _{q}A, \cdot )$
.) It follows from the construction that
$S(\partial _{q}A, \cdot )$
.) It follows from the construction that
![]() $\partial _{q}A$
is non-degenerate because each
$\partial _{q}A$
is non-degenerate because each
![]() $q_i'$
comes from a distinct grouping
$q_i'$
comes from a distinct grouping
![]() $J_i.$
$J_i.$
If
![]() $q=q_{t}$
for some
$q=q_{t}$
for some
![]() $1\leq t\leq k$
, we write
$1\leq t\leq k$
, we write
![]() $\partial _{t}\mathbf {q}$
instead of
$\partial _{t}\mathbf {q}$
instead of
![]() $\mathbf {q}'$
to highlight the fact that we have subtracted the polynomial
$\mathbf {q}'$
to highlight the fact that we have subtracted the polynomial
![]() $q_t$
; we also write
$q_t$
; we also write
![]() $\partial _{t}A$
instead of
$\partial _{t}A$
instead of
![]() $\partial _{q_{t}}A$
to lighten the notation.
$\partial _{q_{t}}A$
to lighten the notation.
Definition 4.6. We say that the operation
![]() $A\to \partial _{t}A$
is 1-inherited if we did not drop
$A\to \partial _{t}A$
is 1-inherited if we did not drop
![]() $q^{\ast }_{1}$
or group it with any other
$q^{\ast }_{1}$
or group it with any other
![]() $q^{\ast }_{i}$
in Step 2. Note that his implies that
$q^{\ast }_{i}$
in Step 2. Note that his implies that
![]() $q^{\prime}_{1}=q^{\ast }_{1}$
and
$q^{\prime}_{1}=q^{\ast }_{1}$
and
![]() $g^{\prime}_{1}=g_{1}$
.
$g^{\prime}_{1}=g_{1}$
.
Example 4.7. Let
![]() $\mathbf {p}=(p_{1},p_{2})$
with
$\mathbf {p}=(p_{1},p_{2})$
with
![]() $p_{1}, p_{2}\colon {\mathbb Z}\to {\mathbb Z}^{d}$
the polynomials given by
$p_{1}, p_{2}\colon {\mathbb Z}\to {\mathbb Z}^{d}$
the polynomials given by
![]() $p_{i}(n)=b_{i,2}n^{2}+b_{i,1}n$
for some
$p_{i}(n)=b_{i,2}n^{2}+b_{i,1}n$
for some
![]() $b_{i,1},b_{i,2}\in {\mathbb Z}^{d}$
for
$b_{i,1},b_{i,2}\in {\mathbb Z}^{d}$
for
![]() $1\leq i\leq 2$
with
$1\leq i\leq 2$
with
![]() $b_{1,2},b_{2,2},b_{1,2}- b_{2,2}\neq \mathbf {0}$
(hence, we have that
$b_{1,2},b_{2,2},b_{1,2}- b_{2,2}\neq \mathbf {0}$
(hence, we have that
![]() $L=1, s=0,$
and
$L=1, s=0,$
and
![]() $k=2$
). We will calculate
$k=2$
). We will calculate
![]() $\partial _2\mathbf {{p}}.$
Subtracting
$\partial _2\mathbf {{p}}.$
Subtracting
![]() $p_2$
in the Step 1 of the vdC operation, we have that
$p_2$
in the Step 1 of the vdC operation, we have that
![]() $\partial _2\mathbf {{p}}=(q_{1},q_{2},q_{3})$
is a tuple of three polynomials,
$\partial _2\mathbf {{p}}=(q_{1},q_{2},q_{3})$
is a tuple of three polynomials,
![]() $q_{1},q_{2},q_{3}\colon {\mathbb Z}^{2}\to {\mathbb Z}^{d},$
given by
$q_{1},q_{2},q_{3}\colon {\mathbb Z}^{2}\to {\mathbb Z}^{d},$
given by
 $$ \begin{align*}\nonumber q_{1}(n,h_1)&=p_1(n+h_1)-p_2(n)\\ &=(b_{1,2}-b_{2,2})n^{2}+2b_{1,2}nh_1+(b_{1,1}-b_{2,1})n+b_{1,1}h_1 +b_{1,2}h_1^{2},\\ q_{2}(n,h_1)&=p_2(n+h_1)-p_2(n)=2b_{2,2}nh_1+b_{2,1}h_1+b_{2,2}h_1^{2}, \\ q_{3}(n,h_1)&=p_1(n)-p_2(n)=(b_{1,2}-b_{2,2})n^{2}+(b_{1,1}-b_{2,1})n, \end{align*} $$
$$ \begin{align*}\nonumber q_{1}(n,h_1)&=p_1(n+h_1)-p_2(n)\\ &=(b_{1,2}-b_{2,2})n^{2}+2b_{1,2}nh_1+(b_{1,1}-b_{2,1})n+b_{1,1}h_1 +b_{1,2}h_1^{2},\\ q_{2}(n,h_1)&=p_2(n+h_1)-p_2(n)=2b_{2,2}nh_1+b_{2,1}h_1+b_{2,2}h_1^{2}, \\ q_{3}(n,h_1)&=p_1(n)-p_2(n)=(b_{1,2}-b_{2,2})n^{2}+(b_{1,1}-b_{2,1})n, \end{align*} $$
where we removed one essentially constant polynomial in Step 2 of the vdC operation. (Here we use
![]() $q_i$
terms instead of
$q_i$
terms instead of
![]() $p^{\prime}_i$
terms in the first step to ease the notation of Example 5.8 that is given in the next section.) Notice that here we have
$p^{\prime}_i$
terms in the first step to ease the notation of Example 5.8 that is given in the next section.) Notice that here we have
![]() $L=1, s'=1,$
and
$L=1, s'=1,$
and
![]() $k'=3.$
$k'=3.$
Actually, as in the example at the beginning of this subsection, after using a series of vdC operations, one can convert
![]() $\mathbf {{p}}$
into a PET-tuple of linear polynomials. Indeed, if we run the vdC operation once more by subtracting
$\mathbf {{p}}$
into a PET-tuple of linear polynomials. Indeed, if we run the vdC operation once more by subtracting
![]() $q_2$
in Step 1 of the vdC operation, we have that
$q_2$
in Step 1 of the vdC operation, we have that
![]() $\partial _2\partial _2\mathbf {{p}}=(q^{\prime}_{1},\ldots ,q^{\prime}_{4})$
is a tuple of four polynomials,
$\partial _2\partial _2\mathbf {{p}}=(q^{\prime}_{1},\ldots ,q^{\prime}_{4})$
is a tuple of four polynomials,
![]() $q^{\prime}_{1},\ldots ,q^{\prime}_{4}\colon {\mathbb Z}^{3}\to {\mathbb Z}^{d},$
given by
$q^{\prime}_{1},\ldots ,q^{\prime}_{4}\colon {\mathbb Z}^{3}\to {\mathbb Z}^{d},$
given by
 $$ \begin{align*} q^{\prime}_{1}(n,h_{1},h_{2}) &=(b_{1,2}-b_{2,2})n^{2}+2(b_{1,2}-b_{2,2})nh_{1}+2(b_{1,2}-b_{2,2})nh_{2}\\ &\quad+(b_{1,1}-b_{2,1}) n+r^{\prime}_{1}(h_{1},h_{2}), \\ q^{\prime}_{2}(n,h_{1},h_{2}) &=(b_{1,2}-b_{2,2})n^{2}-2b_{2,2}nh_{1}+2(b_{1,2}-b_{2,2})nh_{2} \\ &\quad +(b_{1,1}-b_{2,1})n +r^{\prime}_{2}(h_{1},h_{2}), \\ q^{\prime}_{3}(n,h_{1},h_{2})&=(b_{1,2}-b_{2,2})n^{2}+2(b_{1,2}-b_{2,2})nh_{1}+(b_{1,1}-b_{2,1})n+r^{\prime}_{3}(h_{1},h_{2}), \\ q^{\prime}_{4}(n,h_{1},h_{2})&=(b_{1,2}-b_{2,2})n^{2}-2b_{2,2}nh_{1}+(b_{1,1}-b_{2,1})n+r^{\prime}_{4}(h_{1},h_{2}), \end{align*} $$
$$ \begin{align*} q^{\prime}_{1}(n,h_{1},h_{2}) &=(b_{1,2}-b_{2,2})n^{2}+2(b_{1,2}-b_{2,2})nh_{1}+2(b_{1,2}-b_{2,2})nh_{2}\\ &\quad+(b_{1,1}-b_{2,1}) n+r^{\prime}_{1}(h_{1},h_{2}), \\ q^{\prime}_{2}(n,h_{1},h_{2}) &=(b_{1,2}-b_{2,2})n^{2}-2b_{2,2}nh_{1}+2(b_{1,2}-b_{2,2})nh_{2} \\ &\quad +(b_{1,1}-b_{2,1})n +r^{\prime}_{2}(h_{1},h_{2}), \\ q^{\prime}_{3}(n,h_{1},h_{2})&=(b_{1,2}-b_{2,2})n^{2}+2(b_{1,2}-b_{2,2})nh_{1}+(b_{1,1}-b_{2,1})n+r^{\prime}_{3}(h_{1},h_{2}), \\ q^{\prime}_{4}(n,h_{1},h_{2})&=(b_{1,2}-b_{2,2})n^{2}-2b_{2,2}nh_{1}+(b_{1,1}-b_{2,1})n+r^{\prime}_{4}(h_{1},h_{2}), \end{align*} $$
where
![]() $r^{\prime}_{i}\colon {\mathbb Z}^{2}\to {\mathbb Z}^{d}, 1\leq i\leq 4,$
are polynomials in
$r^{\prime}_{i}\colon {\mathbb Z}^{2}\to {\mathbb Z}^{d}, 1\leq i\leq 4,$
are polynomials in
![]() $h_1, h_2$
, and we removed two essentially constant polynomials (that is,
$h_1, h_2$
, and we removed two essentially constant polynomials (that is,
![]() $q_{2}(n,h_1)-q_{2}(n,h_1)$
and
$q_{2}(n,h_1)-q_{2}(n,h_1)$
and
![]() $q_{2}(n+h_{2},h_1)-q_{2}(n,h_1)$
) in Step 2 of the vdC operation.
$q_{2}(n+h_{2},h_1)-q_{2}(n,h_1)$
) in Step 2 of the vdC operation.
Finally, if we apply the vdC operation again by subtracting
![]() $q^{\prime}_4$
in Step 1 of the vdC operation, we have that
$q^{\prime}_4$
in Step 1 of the vdC operation, we have that
![]() $\partial _4\partial _2\partial _2\mathbf {{p}}=(q^{\prime \prime }_{1},\ldots ,q^{\prime \prime }_{7})$
is a tuple of seven polynomials,
$\partial _4\partial _2\partial _2\mathbf {{p}}=(q^{\prime \prime }_{1},\ldots ,q^{\prime \prime }_{7})$
is a tuple of seven polynomials,
![]() $ q^{\prime \prime }_{1},\ldots ,q^{\prime \prime }_{7}\colon {\mathbb Z}^{4}\to {\mathbb Z}^{d},$
given by
$ q^{\prime \prime }_{1},\ldots ,q^{\prime \prime }_{7}\colon {\mathbb Z}^{4}\to {\mathbb Z}^{d},$
given by
 $$ \begin{align*} q^{\prime\prime}_{1}(n,h_{1},h_{2},h_{3}) &=2b_{1,2}nh_{1}\kern1.2pt{+}\kern1.2pt 2(b_{1,2}\kern1.3pt{-}\kern1.3pt b_{2,2})nh_{2}\kern1.3pt{+}\kern1.3pt 2(b_{1,2}\kern1.3pt{-}\kern1.3pt b_{2,2})nh_{3} +r^{\prime\prime}_{1}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{2}(n,h_{1},h_{2},h_{3})&=2(b_{1,2}-b_{2,2})nh_{2}+2(b_{1,2}-b_{2,2})nh_{3} +r^{\prime\prime}_{2}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{3}(n,h_{1},h_{2},h_{3})&=2b_{1,2}nh_{1}+2(b_{1,2}-b_{2,2})nh_{3}+r^{\prime\prime}_{3}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{4}(n,h_{1},h_{2},h_{3})&=2(b_{1,2}-b_{2,2})nh_{3}+r^{\prime\prime}_{4}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{5}(n,h_{1},h_{2},h_{3})&=2b_{1,2}nh_{1}+2(b_{1,2}-b_{2,2})nh_{2}+r^{\prime\prime}_{5}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{6}(n,h_{1},h_{2},h_{3})&=2(b_{1,2}-b_{2,2})nh_{2}+r^{\prime\prime}_{6}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{7}(n,h_{1},h_{2},h_{3})&=2b_{1,2}nh_{1}+r^{\prime\prime}_{7}(h_{1},h_{2},h_{3}), \end{align*} $$
$$ \begin{align*} q^{\prime\prime}_{1}(n,h_{1},h_{2},h_{3}) &=2b_{1,2}nh_{1}\kern1.2pt{+}\kern1.2pt 2(b_{1,2}\kern1.3pt{-}\kern1.3pt b_{2,2})nh_{2}\kern1.3pt{+}\kern1.3pt 2(b_{1,2}\kern1.3pt{-}\kern1.3pt b_{2,2})nh_{3} +r^{\prime\prime}_{1}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{2}(n,h_{1},h_{2},h_{3})&=2(b_{1,2}-b_{2,2})nh_{2}+2(b_{1,2}-b_{2,2})nh_{3} +r^{\prime\prime}_{2}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{3}(n,h_{1},h_{2},h_{3})&=2b_{1,2}nh_{1}+2(b_{1,2}-b_{2,2})nh_{3}+r^{\prime\prime}_{3}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{4}(n,h_{1},h_{2},h_{3})&=2(b_{1,2}-b_{2,2})nh_{3}+r^{\prime\prime}_{4}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{5}(n,h_{1},h_{2},h_{3})&=2b_{1,2}nh_{1}+2(b_{1,2}-b_{2,2})nh_{2}+r^{\prime\prime}_{5}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{6}(n,h_{1},h_{2},h_{3})&=2(b_{1,2}-b_{2,2})nh_{2}+r^{\prime\prime}_{6}(h_{1},h_{2},h_{3}), \\ q^{\prime\prime}_{7}(n,h_{1},h_{2},h_{3})&=2b_{1,2}nh_{1}+r^{\prime\prime}_{7}(h_{1},h_{2},h_{3}), \end{align*} $$
where
![]() $r^{\prime \prime }_{i}\colon {\mathbb Z}^{3}\to {\mathbb Z}^{d}, 1\leq i\leq 7,$
are polynomials in
$r^{\prime \prime }_{i}\colon {\mathbb Z}^{3}\to {\mathbb Z}^{d}, 1\leq i\leq 7,$
are polynomials in
![]() $h_1, h_2, h_3$
, and we removed one essentially constant polynomial in Step 2 of the vdC operation. It is clear that
$h_1, h_2, h_3$
, and we removed one essentially constant polynomial in Step 2 of the vdC operation. It is clear that
![]() $\deg (\partial _4\partial _2\partial _2\mathbf {{p}})=1$
.
$\deg (\partial _4\partial _2\partial _2\mathbf {{p}})=1$
.
The vdC operation provides us with a non-degenerate tuple, the value
![]() $S(\cdot , \cdot )$
of which satisfies the following.
$S(\cdot , \cdot )$
of which satisfies the following.
Proposition 4.8. [Reference Donoso, Koutsogiannis and Sun7, Proposition 4.10]
Let
![]() $(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
$(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
![]() $\mathbb {Z}^{d}$
-system,
$\mathbb {Z}^{d}$
-system,
![]() $A=(L,s,k,\mathbf {g}, \mathbf {q})$
a PET-tuple, and
$A=(L,s,k,\mathbf {g}, \mathbf {q})$
a PET-tuple, and
![]() $q\colon (\mathbb {Z}^{L})^{s+1}\to \mathbb {Z}^{d}$
a polynomial. Then,
$q\colon (\mathbb {Z}^{L})^{s+1}\to \mathbb {Z}^{d}$
a polynomial. Then,
![]() $\partial _{q}A$
is non-degenerate and
$\partial _{q}A$
is non-degenerate and
![]() $S(A,2\tau )\leq 4^{\tau } S(\partial _{q}A,\tau )$
for every
$S(A,2\tau )\leq 4^{\tau } S(\partial _{q}A,\tau )$
for every
![]() $\tau \in {\mathbb N}_0$
.
$\tau \in {\mathbb N}_0$
.
The following crucial result (cf. [Reference Donoso, Koutsogiannis and Sun7, Theorem 4.2]) shows that when we start with a PET-tuple which is 1-standard for a function, then, after finitely many vdC operations, we arrive at a new PET-tuple of degree 1 which is still 1-standard for the same function, so we can then use some Host–Kra seminorm to bound the
![]() $\limsup $
of the average of interest.
$\limsup $
of the average of interest.
Theorem 4.9. Let
![]() $(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
$(X,\mathcal {B},\mu ,(T_{g})_{g\in \mathbb {Z}^{d}})$
be a
![]() $\mathbb {Z}^{d}$
-system and
$\mathbb {Z}^{d}$
-system and
![]() $f\in L^{\infty }(\mu )$
. Let
$f\in L^{\infty }(\mu )$
. Let
![]() $A=(L,s,k,\mathbf {g},\mathbf {q})$
be a non-degenerate PET-tuple which is 1-standard for f. Then, there exist
$A=(L,s,k,\mathbf {g},\mathbf {q})$
be a non-degenerate PET-tuple which is 1-standard for f. Then, there exist
![]() $\rho _{1},\ldots ,\rho _{t}\in \mathbb {N},$
for some
$\rho _{1},\ldots ,\rho _{t}\in \mathbb {N},$
for some
![]() $t\in \mathbb {N}_0$
depending only on
$t\in \mathbb {N}_0$
depending only on
![]() $\deg (A),L,s,k$
, such that for all
$\deg (A),L,s,k$
, such that for all
![]() $1\leq t'\leq t$
,
$1\leq t'\leq t$
,
![]() $\partial _{\rho _{t'}}\ldots \partial _{\rho _{1}}A$
is a non-degenerate PET-tuple which is still 1-standard for f, and that
$\partial _{\rho _{t'}}\ldots \partial _{\rho _{1}}A$
is a non-degenerate PET-tuple which is still 1-standard for f, and that
![]() $\partial _{\rho _{t'-1}}\ldots \partial _{\rho _{1}}A\to \partial _{\rho _{t'}}\ldots \partial _{\rho _{1}}A$
is 1-inherited. Moreover,
$\partial _{\rho _{t'-1}}\ldots \partial _{\rho _{1}}A\to \partial _{\rho _{t'}}\ldots \partial _{\rho _{1}}A$
is 1-inherited. Moreover,
![]() $\deg (\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A)=1$
.
$\deg (\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A)=1$
.
Remark 4.10. The dependence of t on
![]() $\deg (A),L,s,k$
was not stated in [Reference Donoso, Koutsogiannis and Sun7, Theorem 4.2], but it follows immediately from its proof. Also,
$\deg (A),L,s,k$
was not stated in [Reference Donoso, Koutsogiannis and Sun7, Theorem 4.2], but it follows immediately from its proof. Also,
![]() $\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A$
is understood as A if
$\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A$
is understood as A if
![]() $t=0$
. Notice also that in Theorem 4.9, we need every step of the vdC operation to be 1-inherited. Otherwise, we would have to either drop f or combine it with other functions in some of the induction steps; in the end, that would prevent us from obtaining an upper bound for
$t=0$
. Notice also that in Theorem 4.9, we need every step of the vdC operation to be 1-inherited. Otherwise, we would have to either drop f or combine it with other functions in some of the induction steps; in the end, that would prevent us from obtaining an upper bound for
![]() $S(A,1)$
by some Host–Kra seminorm of f. In [Reference Donoso, Koutsogiannis and Sun7, Theorem 4.2], the PET tuple is not required to be 1-standard nor 1-inherited; this comes at no extra cost as the polynomials chosen at each step to run the vdC operation are of minimum degree.
$S(A,1)$
by some Host–Kra seminorm of f. In [Reference Donoso, Koutsogiannis and Sun7, Theorem 4.2], the PET tuple is not required to be 1-standard nor 1-inherited; this comes at no extra cost as the polynomials chosen at each step to run the vdC operation are of minimum degree.
If A is an m-standard PET-tuple for the function
![]() $f,$
then, by rearranging the terms if necessary, one can get a new tuple
$f,$
then, by rearranging the terms if necessary, one can get a new tuple
![]() $A'$
which is 1-standard for f with
$A'$
which is 1-standard for f with
![]() $S(A,\tau )=S(A',\tau )$
. However, if A is semi-standard but not standard for f, then the PET-induction does not work well enough to provide an upper bound for
$S(A,\tau )=S(A',\tau )$
. However, if A is semi-standard but not standard for f, then the PET-induction does not work well enough to provide an upper bound for
![]() $S(A,\tau )$
in terms of some Host–Kra seminorm of f. To overcome this difficulty one follows [Reference Donoso, Koutsogiannis and Sun7]. More specifically, using [Reference Donoso, Koutsogiannis and Sun7, Proposition 6.3], which is a ‘dimension-increment’ argument, A can be transformed into a new PET-tuple which is 1-standard for f (at the cost of increasing the dimension from L to
$S(A,\tau )$
in terms of some Host–Kra seminorm of f. To overcome this difficulty one follows [Reference Donoso, Koutsogiannis and Sun7]. More specifically, using [Reference Donoso, Koutsogiannis and Sun7, Proposition 6.3], which is a ‘dimension-increment’ argument, A can be transformed into a new PET-tuple which is 1-standard for f (at the cost of increasing the dimension from L to
![]() $2L$
which is harmless for our approach). So, following this procedure, for any fixed function
$2L$
which is harmless for our approach). So, following this procedure, for any fixed function
![]() $f,$
we may assume without loss of generality that the corresponding polynomial iterate p is of maximum degree, making the PET-tuple, after potential rearrangement of its terms,
$f,$
we may assume without loss of generality that the corresponding polynomial iterate p is of maximum degree, making the PET-tuple, after potential rearrangement of its terms,
![]() $1$
-standard for f. A combination of the previous results will allow us to obtain the required upper bound for each function.
$1$
-standard for f. A combination of the previous results will allow us to obtain the required upper bound for each function.
5 Finding a characteristic factor
This lengthy section is dedicated to proving Theorem 2.11. To this end, we need to show two intermediate results, that is, Propositions 5.2 and 5.4, which improve two technical results from [Reference Donoso, Koutsogiannis and Sun7], namely [Reference Donoso, Koutsogiannis and Sun7, Proposition 5.6] and [Reference Donoso, Koutsogiannis and Sun7, Proposition 5.5], respectively.
Recall that for a subset A of
![]() $\mathbb {Q}^{d}$
,
$\mathbb {Q}^{d}$
,
![]() $G(A)=\text {span}_{{\mathbb Q}}\{a\in A\}\cap {\mathbb Z}^{d}.$
Let
$G(A)=\text {span}_{{\mathbb Q}}\{a\in A\}\cap {\mathbb Z}^{d}.$
Let
![]() $G'(A):=\text {span}_{{\mathbb Z}}\{a\in ~A\}$
.
$G'(A):=\text {span}_{{\mathbb Z}}\{a\in ~A\}$
.
Convention 5.1. For the rest of the paper, for every
![]() $\mathbf {u}_{i}=(u_{i,1},\ldots ,u_{i,L})\in ({\mathbb Q}^{d})^{L}, 1\leq i\leq r$
, we denote
$\mathbf {u}_{i}=(u_{i,1},\ldots ,u_{i,L})\in ({\mathbb Q}^{d})^{L}, 1\leq i\leq r$
, we denote ![]() and
and ![]()
The first result, which enhances [Reference Donoso, Koutsogiannis and Sun7, Proposition 5.6], gives a bound for the average of interest by finite step seminorms (recall Convention 3.3 for notions on Host–Kra seminorms). To pass from infinite step seminorms to finite step ones, we use the implications of Propositions 3.6 and 3.8.
Proposition 5.2. (Bounding averaged Host–Kra seminorms by a single one)
Let
![]() $s,s',t,L\in \mathbb {N}$
and
$s,s',t,L\in \mathbb {N}$
and
![]() ${\mathbf {c}}_{m}\colon (\mathbb {Z}^{L})^{s}\to (\mathbb {Z}^{d})^{L}, 1\leq m\leq t,$
be polynomials with
${\mathbf {c}}_{m}\colon (\mathbb {Z}^{L})^{s}\to (\mathbb {Z}^{d})^{L}, 1\leq m\leq t,$
be polynomials with
![]() ${\mathbf {c}}_{m}\neq \mathbf {0}$
given by
${\mathbf {c}}_{m}\neq \mathbf {0}$
given by
 $$ \begin{align} {\mathbf{c}}_{m}(h_{1},\ldots,h_{s})=\sum_{a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L},\vert a_{1}\vert+\cdots+\vert a_{s}\vert\leq s'}h^{a_{1}}_{1}\ldots h^{a_{s}}_{s}\cdot \mathbf{u}_{m}(a_{1},\ldots,a_{s}) \end{align} $$
$$ \begin{align} {\mathbf{c}}_{m}(h_{1},\ldots,h_{s})=\sum_{a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L},\vert a_{1}\vert+\cdots+\vert a_{s}\vert\leq s'}h^{a_{1}}_{1}\ldots h^{a_{s}}_{s}\cdot \mathbf{u}_{m}(a_{1},\ldots,a_{s}) \end{align} $$
for some
Denote
There exists
![]() $D\in {\mathbb N}_0$
depending only on
$D\in {\mathbb N}_0$
depending only on
![]() $s,s',L,t$
such that for every
$s,s',L,t$
such that for every
![]() $\mathbb {Z}^{d}$
-system
$\mathbb {Z}^{d}$
-system
![]() $(X,\mathcal {B},\mu , (T_{g})_{g\in \mathbb {Z}^{d}})$
and every
$(X,\mathcal {B},\mu , (T_{g})_{g\in \mathbb {Z}^{d}})$
and every
![]() $f\in L^{\infty }(\mu )$
,
$f\in L^{\infty }(\mu )$
,
Remark 5.3.
![]() $H_{m}$
is dependent only on those
$H_{m}$
is dependent only on those
![]() $u_{m,i}(a_{1},\ldots ,a_{s})$
with
$u_{m,i}(a_{1},\ldots ,a_{s})$
with
![]() $\vert a_{1}\vert +\cdots + \vert a_{s}\vert \leq s'$
.
$\vert a_{1}\vert +\cdots + \vert a_{s}\vert \leq s'$
.
We start by explaining the idea behind Proposition 5.2 with an example, which also illustrates how Proposition 5.2 improves [Reference Donoso, Koutsogiannis and Sun7, Propositions 5.5 and 5.6].
Example 5.4. Let
![]() $p_{1},p_{2}\colon {\mathbb Z}\to {\mathbb Z}^{2}$
be polynomials given by
$p_{1},p_{2}\colon {\mathbb Z}\to {\mathbb Z}^{2}$
be polynomials given by
![]() $p_{1}(n)=(n^{2}+n,0)$
and
$p_{1}(n)=(n^{2}+n,0)$
and
![]() $p_{2}(n)=(0,n^{2})$
, and
$p_{2}(n)=(0,n^{2})$
, and
![]() $(X,\mathcal {B},\mu ,(T_{g})_{g\in {\mathbb Z}^{2}})$
be a
$(X,\mathcal {B},\mu ,(T_{g})_{g\in {\mathbb Z}^{2}})$
be a
![]() ${\mathbb Z}^{2}$
-system. Consider the following expression:
${\mathbb Z}^{2}$
-system. Consider the following expression:
 $$ \begin{align*}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}} T_{p_{1}(n)}f_1\cdot T_{p_{2}(n)}f_2 \Vert_{2}.\end{align*} $$
$$ \begin{align*}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}} T_{p_{1}(n)}f_1\cdot T_{p_{2}(n)}f_2 \Vert_{2}.\end{align*} $$
Put
![]() $e_{1}=(1,0)$
,
$e_{1}=(1,0)$
,
![]() $e_{2}=(0,1)$
, and
$e_{2}=(0,1)$
, and
![]() $e=(1,-1)$
. Similarly to the computation in [Reference Donoso, Koutsogiannis and Sun7, Second part of computations for Example 1], we get
$e=(1,-1)$
. Similarly to the computation in [Reference Donoso, Koutsogiannis and Sun7, Second part of computations for Example 1], we get
 $$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}} T_{p_{1}(n)}f_1\cdot T_{p_{2}(n)}f_2 \Vert_{2}^{8} \leq C \cdot \overline{\mathbb{E}}^{\square}_{\mathbf{h}\in\mathbb{Z}^{3}} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_{1}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{G'({\mathbf{c}}_{1}(\mathbf{h})),\ldots, G'({\mathbf{c}}_{7}(\mathbf{h}))}, \end{align} $$
$$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}} T_{p_{1}(n)}f_1\cdot T_{p_{2}(n)}f_2 \Vert_{2}^{8} \leq C \cdot \overline{\mathbb{E}}^{\square}_{\mathbf{h}\in\mathbb{Z}^{3}} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_{1}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{G'({\mathbf{c}}_{1}(\mathbf{h})),\ldots, G'({\mathbf{c}}_{7}(\mathbf{h}))}, \end{align} $$
where C is a universal constant, and
 $$ \begin{align*}\nonumber & {\mathbf{c}}_{1}(h_{1},h_{2},h_{3})=-2h_{1}e_{1}, \\& {\mathbf{c}}_{2}(h_{1},h_{2},h_{3})=2h_{2}e, \\& {\mathbf{c}}_{3}(h_{1},h_{2},h_{3})=-2h_{1}e_{1}+2h_{2}e, \\& {\mathbf{c}}_{4}(h_{1},h_{2},h_{3})=2h_{3}e, \\& {\mathbf{c}}_{5}(h_{1},h_{2},h_{3})=-2h_{1}e_{1}+2h_{3}e, \\& {\mathbf{c}}_{6}(h_{1},h_{2},h_{3})=2(h_{2}+h_{3})e, \\& {\mathbf{c}}_{7}(h_{1},h_{2},h_{3})=-2h_{1}e_{1}+2(h_{2}+h_{3})e. \end{align*} $$
$$ \begin{align*}\nonumber & {\mathbf{c}}_{1}(h_{1},h_{2},h_{3})=-2h_{1}e_{1}, \\& {\mathbf{c}}_{2}(h_{1},h_{2},h_{3})=2h_{2}e, \\& {\mathbf{c}}_{3}(h_{1},h_{2},h_{3})=-2h_{1}e_{1}+2h_{2}e, \\& {\mathbf{c}}_{4}(h_{1},h_{2},h_{3})=2h_{3}e, \\& {\mathbf{c}}_{5}(h_{1},h_{2},h_{3})=-2h_{1}e_{1}+2h_{3}e, \\& {\mathbf{c}}_{6}(h_{1},h_{2},h_{3})=2(h_{2}+h_{3})e, \\& {\mathbf{c}}_{7}(h_{1},h_{2},h_{3})=-2h_{1}e_{1}+2(h_{2}+h_{3})e. \end{align*} $$
Using [Reference Donoso, Koutsogiannis and Sun7, Proposition 5.6], one can show that if
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_{1}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{e^{\times D}_{1},e^{\times D}}=0$
for all
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_{1}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{e^{\times D}_{1},e^{\times D}}=0$
for all
![]() $D\in {\mathbb N}$
, then the right-hand side of equation (19) is 0. In this paper, we strengthen this result by only assuming that
$D\in {\mathbb N}$
, then the right-hand side of equation (19) is 0. In this paper, we strengthen this result by only assuming that
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_{1}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{e^{\times D}_{1},e^{\times D}}=0$
for some
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_{1}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{e^{\times D}_{1},e^{\times D}}=0$
for some
![]() $D\in {\mathbb N}$
.
$D\in {\mathbb N}$
.
Indeed,
![]() $Z_{\{G'({\mathbf {c}}_{i}(\mathbf {h}),{\mathbf {c}}_{j}(\mathbf {h'}))\}_{1\leq i,j\leq 7}}=Z_{\{G({\mathbf {c}}_{i}(\mathbf {h}),{\mathbf {c}}_{j}(\mathbf {h'}))\}_{1\leq i,j\leq 7}}$
by Proposition 3.1. Using Proposition 3.8 (for
$Z_{\{G'({\mathbf {c}}_{i}(\mathbf {h}),{\mathbf {c}}_{j}(\mathbf {h'}))\}_{1\leq i,j\leq 7}}=Z_{\{G({\mathbf {c}}_{i}(\mathbf {h}),{\mathbf {c}}_{j}(\mathbf {h'}))\}_{1\leq i,j\leq 7}}$
by Proposition 3.1. Using Proposition 3.8 (for
![]() $I=[-N,N]^{3},$
letting
$I=[-N,N]^{3},$
letting
![]() $N\to \infty $
) and Corollary 3.7, we have that the right-hand side of equation (19) is 0 if
$N\to \infty $
) and Corollary 3.7, we have that the right-hand side of equation (19) is 0 if
for a density 1 subset of
![]() $(h,h')\in ({\mathbb Z}^{3})^2$
. Indeed, Proposition 3.8 implies that the right-hand side of equation (19) is 0 if
$(h,h')\in ({\mathbb Z}^{3})^2$
. Indeed, Proposition 3.8 implies that the right-hand side of equation (19) is 0 if
![]() ${\overline {\mathbb {E}}}_{\mathbf {h},\mathbf {h}'\in {\mathbb Z}^{3}}^{\square }\Vert \mathbb {E}(f\vert Z_{\{G({\mathbf {c}}_{i}(\mathbf {h}))+G({\mathbf {c}}_{j}(\mathbf {h'}))\}_{1\leq i,j\leq 7}})\Vert ^{2}_{2}=0.$
However, by Remark 3.10,
${\overline {\mathbb {E}}}_{\mathbf {h},\mathbf {h}'\in {\mathbb Z}^{3}}^{\square }\Vert \mathbb {E}(f\vert Z_{\{G({\mathbf {c}}_{i}(\mathbf {h}))+G({\mathbf {c}}_{j}(\mathbf {h'}))\}_{1\leq i,j\leq 7}})\Vert ^{2}_{2}=0.$
However, by Remark 3.10,
![]() $G({\mathbf {c}}_{i}(\mathbf {h}))+G({\mathbf {c}}_{j}(\mathbf {h'}))$
is a finite index subgroup of
$G({\mathbf {c}}_{i}(\mathbf {h}))+G({\mathbf {c}}_{j}(\mathbf {h'}))$
is a finite index subgroup of
![]() $G({\mathbf {c}}_{i}(\mathbf {h}),{\mathbf {c}}_{j}(\mathbf {h'}))$
, so we can use Lemma 3.9(iv) to conclude that
$G({\mathbf {c}}_{i}(\mathbf {h}),{\mathbf {c}}_{j}(\mathbf {h'}))$
, so we can use Lemma 3.9(iv) to conclude that
![]() $\Vert \mathbb {E}(f\vert Z_{\{G({\mathbf {c}}_{i}(\mathbf {h}))+G({\mathbf {c}}_{j}(\mathbf {h'}))\}_{1\leq i,j\leq 7}})\Vert ^{2}_{2}=0$
for a density 1 subset of
$\Vert \mathbb {E}(f\vert Z_{\{G({\mathbf {c}}_{i}(\mathbf {h}))+G({\mathbf {c}}_{j}(\mathbf {h'}))\}_{1\leq i,j\leq 7}})\Vert ^{2}_{2}=0$
for a density 1 subset of
![]() $(h,h')\in ({\mathbb Z}^{3})^2$
, which implies that the average over
$(h,h')\in ({\mathbb Z}^{3})^2$
, which implies that the average over
![]() $h,h'$
is 0 too.
$h,h'$
is 0 too.
However, for ‘almost all’
![]() $\mathbf {h},\mathbf {h}'\in {\mathbb Z}^{3}$
, the group
$\mathbf {h},\mathbf {h}'\in {\mathbb Z}^{3}$
, the group
![]() $G({\mathbf {c}}_{i}(\mathbf {h}),{\mathbf {c}}_{j}(\mathbf {h'}))$
equals
$G({\mathbf {c}}_{i}(\mathbf {h}),{\mathbf {c}}_{j}(\mathbf {h'}))$
equals
![]() ${\mathbb Z} e_{1}$
if
${\mathbb Z} e_{1}$
if
![]() $i=j=1$
,
$i=j=1$
,
![]() ${\mathbb Z} e$
if
${\mathbb Z} e$
if
![]() $i,j\in \{2,4,6\}$
and
$i,j\in \{2,4,6\}$
and
![]() ${\mathbb Z}^{2}$
otherwise. So,
${\mathbb Z}^{2}$
otherwise. So,
![]() $Z_{\{G({\mathbf {c}}_{i}(\mathbf {h}),{\mathbf {c}}_{j}(\mathbf {h'}))\}_{1\leq i,j\leq 7}}$
is contained in
$Z_{\{G({\mathbf {c}}_{i}(\mathbf {h}),{\mathbf {c}}_{j}(\mathbf {h'}))\}_{1\leq i,j\leq 7}}$
is contained in
![]() $Z_{e_{1},e^{\times 9},({\mathbb Z}^{2})^{\times 39}}$
, which is contained in
$Z_{e_{1},e^{\times 9},({\mathbb Z}^{2})^{\times 39}}$
, which is contained in
![]() $Z_{e_{1}^{\times 25},e^{\times 25}}$
by Proposition 3.1. Hence, the right-hand side of equation (19) is
$Z_{e_{1}^{\times 25},e^{\times 25}}$
by Proposition 3.1. Hence, the right-hand side of equation (19) is
![]() $0$
if
$0$
if
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_{1}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{e_{1}^{\times 25},e^{\times 25}}=0$
.
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_{1}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{e_{1}^{\times 25},e^{\times 25}}=0$
.
We now prove the general case.
Proof of Proposition 5.2
Since
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{G'({\mathbf {c}}_{1}(h_{1},\ldots ,h_{s}))}\leq \lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{G'({\mathbf {c}}_{1}(h_{1},\ldots ,h_{s})),G'({\mathbf {c}}_{1}(h_{1},\ldots ,h_{s}))}$
by Proposition 3.1, duplicating
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{G'({\mathbf {c}}_{1}(h_{1},\ldots ,h_{s}))}\leq \lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{G'({\mathbf {c}}_{1}(h_{1},\ldots ,h_{s})),G'({\mathbf {c}}_{1}(h_{1},\ldots ,h_{s}))}$
by Proposition 3.1, duplicating
![]() ${\mathbf {c}}_{1}$
if necessary, we may assume without loss of generality that
${\mathbf {c}}_{1}$
if necessary, we may assume without loss of generality that
![]() $t\geq 2$
. We may also assume that
$t\geq 2$
. We may also assume that
![]() $\|f\|_{L^{\infty }(\mu )}\leq 1$
. Following our notational convention, denote
$\|f\|_{L^{\infty }(\mu )}\leq 1$
. Following our notational convention, denote ![]() . Using Proposition 3.8 and Corollary 3.7 for
. Using Proposition 3.8 and Corollary 3.7 for
![]() $I=([-N,N]^{L})^{s},$
and then letting
$I=([-N,N]^{L})^{s},$
and then letting
![]() $N\to \infty $
, for all
$N\to \infty $
, for all
![]() $W=2^w, w\in \mathbb {N},$
we have that
$W=2^w, w\in \mathbb {N},$
we have that
 $$ \begin{align} & ({\overline{\mathbb{E}}}^{\square}_{\mathbf{h}\in(\mathbb{Z}^{L})^{s}}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{\{G'({\mathbf{c}}_{m}(\mathbf{h}))\}_{1\leq m\leq t}})^{2^{t}W} \nonumber\\ &\quad \leq ({\overline{\mathbb{E}}}^{\square}_{\mathbf{h}\in (\mathbb{Z}^{L})^s}\Vert \mathbb{E}(f\vert Z_{\{ G'({\mathbf{c}}_{m}(\mathbf{h}))\}_{1\leq m\leq t}})\Vert^{2}_{2})^W \\ &\quad \leq {\overline{\mathbb{E}}}^{\square}_{\mathbf{h}^{1},\ldots,\mathbf{h}^{W}\in (\mathbb{Z}^{L})^{s}}\Vert \mathbb{E}(f\vert Z_{\{G'({\mathbf{c}}_{m_{1}}(\mathbf{h}^{1}))+\cdots+G'({\mathbf{c}}_{m_{W}}(\mathbf{h}^{W}))\}_{1\leq m_{1},\ldots,m_{W}\leq t}})\Vert^{2}_{2}.\nonumber \end{align} $$
$$ \begin{align} & ({\overline{\mathbb{E}}}^{\square}_{\mathbf{h}\in(\mathbb{Z}^{L})^{s}}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{\{G'({\mathbf{c}}_{m}(\mathbf{h}))\}_{1\leq m\leq t}})^{2^{t}W} \nonumber\\ &\quad \leq ({\overline{\mathbb{E}}}^{\square}_{\mathbf{h}\in (\mathbb{Z}^{L})^s}\Vert \mathbb{E}(f\vert Z_{\{ G'({\mathbf{c}}_{m}(\mathbf{h}))\}_{1\leq m\leq t}})\Vert^{2}_{2})^W \\ &\quad \leq {\overline{\mathbb{E}}}^{\square}_{\mathbf{h}^{1},\ldots,\mathbf{h}^{W}\in (\mathbb{Z}^{L})^{s}}\Vert \mathbb{E}(f\vert Z_{\{G'({\mathbf{c}}_{m_{1}}(\mathbf{h}^{1}))+\cdots+G'({\mathbf{c}}_{m_{W}}(\mathbf{h}^{W}))\}_{1\leq m_{1},\ldots,m_{W}\leq t}})\Vert^{2}_{2}.\nonumber \end{align} $$
We claim that this last expression equals 0 if
for a density 1 set of
![]() $(\mathbf {h}^{1},\ldots ,\mathbf {h}^{W})\in ({\mathbb Z}^L)^{sW}.$
Note that this is equivalent to
$(\mathbf {h}^{1},\ldots ,\mathbf {h}^{W})\in ({\mathbb Z}^L)^{sW}.$
Note that this is equivalent to
for a density 1 set of
![]() $(\mathbf {h}^{1},\ldots ,\mathbf {h}^{W})\in ({\mathbb Z}^L)^{sW}$
, since by Proposition 3.1(v) and (vi), noting that
$(\mathbf {h}^{1},\ldots ,\mathbf {h}^{W})\in ({\mathbb Z}^L)^{sW}$
, since by Proposition 3.1(v) and (vi), noting that
![]() $t\geq 2$
, for every
$t\geq 2$
, for every
![]() $(\mathbf {h}^{1},\ldots ,\mathbf {h}^{W})\in \Omega $
, we have that
$(\mathbf {h}^{1},\ldots ,\mathbf {h}^{W})\in \Omega $
, we have that
![]() $Z_{\{G({\mathbf {c}}_{m_{1}}(\mathbf {h}^{1}),\ldots ,{\mathbf {c}}_{m_{W}}(\mathbf {h}^{W}))\}_{1\leq m_{1},\ldots ,m_{W}\leq t}}= Z_{\{G'({\mathbf {c}}_{m_{1}}(\mathbf {h}^{1}),\ldots ,{\mathbf {c}}_{m_{W}}(\mathbf {h}^{W}))\}_{1\leq m_{1},\ldots ,m_{W}\leq t}}$
.
$Z_{\{G({\mathbf {c}}_{m_{1}}(\mathbf {h}^{1}),\ldots ,{\mathbf {c}}_{m_{W}}(\mathbf {h}^{W}))\}_{1\leq m_{1},\ldots ,m_{W}\leq t}}= Z_{\{G'({\mathbf {c}}_{m_{1}}(\mathbf {h}^{1}),\ldots ,{\mathbf {c}}_{m_{W}}(\mathbf {h}^{W}))\}_{1\leq m_{1},\ldots ,m_{W}\leq t}}$
.
Analogously to Example 5.4 via Remark 3.10, and Lemma 3.9(iv), this last condition implies that the last line of equation (20) is equal to 0.
Let w be the smallest integer such that
![]() $2^{w}\geq t(s'+1)^{sL}$
and
$2^{w}\geq t(s'+1)^{sL}$
and
![]() $\Omega $
the set of
$\Omega $
the set of
![]() $(\mathbf {h}^{1},\ldots , \mathbf {h}^{W}) \in ({\mathbb Z}^{sL})^{W}\!$
such that for every
$(\mathbf {h}^{1},\ldots , \mathbf {h}^{W}) \in ({\mathbb Z}^{sL})^{W}\!$
such that for every
![]() $1\!\leq m_{1},\ldots ,m_{W}\leq t$
, the group
$1\!\leq m_{1},\ldots ,m_{W}\leq t$
, the group
![]() $G({\mathbf {c}}_{m_{1}}(\mathbf {h}^{1}), \ldots , {\mathbf {c}}_{m_{W}}(\mathbf {h}^{W}))$
contains at least one of
$G({\mathbf {c}}_{m_{1}}(\mathbf {h}^{1}), \ldots , {\mathbf {c}}_{m_{W}}(\mathbf {h}^{W}))$
contains at least one of
![]() $H_{1},\ldots ,H_{t}$
. Then,
$H_{1},\ldots ,H_{t}$
. Then,
![]() $Z_{\{G({\mathbf {c}}_{m_{1}}(\mathbf {h}^{1}),\ldots , {\mathbf {c}}_{m_{W}} (\mathbf {h}^{W}))\}_{1\leq m_{1},\ldots ,m_{W}\leq t}}$
is a factor of
$Z_{\{G({\mathbf {c}}_{m_{1}}(\mathbf {h}^{1}),\ldots , {\mathbf {c}}_{m_{W}} (\mathbf {h}^{W}))\}_{1\leq m_{1},\ldots ,m_{W}\leq t}}$
is a factor of
![]() $Z_{H^{\times D}_{1},\ldots ,H^{\times D}_{t}}$
for
$Z_{H^{\times D}_{1},\ldots ,H^{\times D}_{t}}$
for ![]() , and thus
, and thus
![]() $\mathbb {E}(f\vert Z_{\{G({\mathbf {c}}_{m_{1}}(\mathbf {h}^{1}),\ldots ,{\mathbf {c}}_{m_{W}}(\mathbf {h}^{W}))\}_{1\leq m_{1},\ldots ,m_{W}\leq t}}) =0$
since
$\mathbb {E}(f\vert Z_{\{G({\mathbf {c}}_{m_{1}}(\mathbf {h}^{1}),\ldots ,{\mathbf {c}}_{m_{W}}(\mathbf {h}^{W}))\}_{1\leq m_{1},\ldots ,m_{W}\leq t}}) =0$
since
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H^{\times D}_{1},\ldots ,H^{\times D}_{t}}=0$
. So, to show that the first line of equation (20) is equal to 0, it suffices to show that
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert _{H^{\times D}_{1},\ldots ,H^{\times D}_{t}}=0$
. So, to show that the first line of equation (20) is equal to 0, it suffices to show that
![]() $\Omega $
is of upper density 1.
$\Omega $
is of upper density 1.
Let ![]() and
and
![]() $1\leq m_{1},\ldots ,m_{W}\leq t$
. By the pigeonhole principle, at least
$1\leq m_{1},\ldots ,m_{W}\leq t$
. By the pigeonhole principle, at least
![]() $(s'+1)^{sL}$
many of the
$(s'+1)^{sL}$
many of the
![]() $m_{1},\ldots ,m_{W}$
take the same value. Assume that
$m_{1},\ldots ,m_{W}$
take the same value. Assume that
![]() $m_{i_{1}}=\cdots =m_{i_{W'}}=m$
, where
$m_{i_{1}}=\cdots =m_{i_{W'}}=m$
, where
![]() $W'\leq (s'+1)^{sL}$
is the number of
$W'\leq (s'+1)^{sL}$
is the number of
![]() $a_{1},\ldots ,a_{s}\in \mathbb {N}_0^{L}$
with
$a_{1},\ldots ,a_{s}\in \mathbb {N}_0^{L}$
with
![]() $\vert a_{1}\vert +\cdots +\vert a_{s}\vert \leq s'$
. Note that
$\vert a_{1}\vert +\cdots +\vert a_{s}\vert \leq s'$
. Note that
![]() $W'$
depends only on
$W'$
depends only on
![]() $s',s$
and L. Write
$s',s$
and L. Write ![]() and consider the
and consider the
![]() $W'\times W'$
matrix
$W'\times W'$
matrix
If
![]() $\det (A_{i_{1},\ldots ,i_{W'}}(\tilde {\mathbf {h}}))\neq 0$
, then by the definition of
$\det (A_{i_{1},\ldots ,i_{W'}}(\tilde {\mathbf {h}}))\neq 0$
, then by the definition of
![]() ${\mathbf {c}}_{m}(\mathbf {h})$
in equation (17) and knowledge of linear algebra, each vector in
${\mathbf {c}}_{m}(\mathbf {h})$
in equation (17) and knowledge of linear algebra, each vector in
![]() $H_{m}$
can be written as a linear combination of
$H_{m}$
can be written as a linear combination of
![]() ${\mathbf {c}}_{m}(\mathbf {h}^{i_{1}}),\ldots ,{\mathbf {c}}_{m}(\mathbf {h}^{i_{W'}})$
with rational coefficients. So, using Convention 5.1, we have that
${\mathbf {c}}_{m}(\mathbf {h}^{i_{1}}),\ldots ,{\mathbf {c}}_{m}(\mathbf {h}^{i_{W'}})$
with rational coefficients. So, using Convention 5.1, we have that
In conclusion,
![]() $\tilde {\mathbf {h}}\in \Omega $
if for all
$\tilde {\mathbf {h}}\in \Omega $
if for all
![]() $1\leq i_{1}< \cdots < i_{W'}\leq W$
,
$1\leq i_{1}< \cdots < i_{W'}\leq W$
,
![]() $\det (A_{i_{1},\ldots ,i_{W'}}(\tilde {\mathbf {h}}))\neq 0$
.
$\det (A_{i_{1},\ldots ,i_{W'}}(\tilde {\mathbf {h}}))\neq 0$
.
Thus, it suffices to show that for all
![]() $1\leq i_{1}< \cdots < i_{W'}\leq W$
, the set of
$1\leq i_{1}< \cdots < i_{W'}\leq W$
, the set of
![]() $\tilde {\mathbf {h}}\in ({\mathbb Z}^{sL})^{W}$
with
$\tilde {\mathbf {h}}\in ({\mathbb Z}^{sL})^{W}$
with
![]() $\det (A_{i_{1},\ldots ,i_{W'}}(\tilde {\mathbf {h}}))=0$
is of density 0. We may assume without loss of generality that
$\det (A_{i_{1},\ldots ,i_{W'}}(\tilde {\mathbf {h}}))=0$
is of density 0. We may assume without loss of generality that
![]() $i_{1}=1,\ldots , i_{W'}=W'$
. Note that
$i_{1}=1,\ldots , i_{W'}=W'$
. Note that
![]() $\det (A_{1,\ldots ,W'}(\tilde {\mathbf {h}}))$
is a polynomial in
$\det (A_{1,\ldots ,W'}(\tilde {\mathbf {h}}))$
is a polynomial in
![]() $h_{i,j}, 1\leq i\leq W', 1\leq j\leq s$
. Looking at the term
$h_{i,j}, 1\leq i\leq W', 1\leq j\leq s$
. Looking at the term
![]() $h_{1,1}^{(s,0,\ldots ,0)}h_{2,2}^{(s,0,\ldots ,0)}\cdots h_{W',W'}^{(s,0,\ldots ,0)}$
, we see that
$h_{1,1}^{(s,0,\ldots ,0)}h_{2,2}^{(s,0,\ldots ,0)}\cdots h_{W',W'}^{(s,0,\ldots ,0)}$
, we see that
![]() $\det (A_{1,\ldots ,W'}(\tilde {\mathbf {h}}))$
is a non-constant polynomial. Therefore, the set of solutions to
$\det (A_{1,\ldots ,W'}(\tilde {\mathbf {h}}))$
is a non-constant polynomial. Therefore, the set of solutions to
![]() $\det (A_{1,\ldots ,W'}(\tilde {\mathbf {h}}))=0$
is of 0 density by Lemma 3.11, which completes the argument.
$\det (A_{1,\ldots ,W'}(\tilde {\mathbf {h}}))=0$
is of 0 density by Lemma 3.11, which completes the argument.
The second statement, which strengthens [Reference Donoso, Koutsogiannis and Sun7, Proposition 5.5], is the following (see Definition 2.1 for the various notions appearing in the statement).
Proposition 5.5. (Bounding the average by averaged Host–Kra seminorms)
Let
![]() $d,k,K,L\in \mathbb {N}, \mathbf {p}=(p_{1},\ldots ,p_{k})$
,
$d,k,K,L\in \mathbb {N}, \mathbf {p}=(p_{1},\ldots ,p_{k})$
,
![]() $p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be a family of essentially distinct polynomials of degrees at most
$p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be a family of essentially distinct polynomials of degrees at most
![]() $K,$
with
$K,$
with
![]() $p_{i}(n)=\sum _{v\in \mathbb {N}_0^{L}, \vert v\vert \leq K}b_{i,v}n^{v}$
for some
$p_{i}(n)=\sum _{v\in \mathbb {N}_0^{L}, \vert v\vert \leq K}b_{i,v}n^{v}$
for some
![]() $b_{i,v}\in \mathbb {Q}^{d}$
. There exist
$b_{i,v}\in \mathbb {Q}^{d}$
. There exist
![]() $s,s',t_{1},\ldots ,t_{k}\in \mathbb {N}$
, depending only on
$s,s',t_{1},\ldots ,t_{k}\in \mathbb {N}$
, depending only on
![]() $d,k,K,L$
, and polynomials
$d,k,K,L$
, and polynomials
![]() ${\mathbf {c}}_{i,m}\colon (\mathbb {Z}^{L})^{s}\to (\mathbb {Z}^{d})^{L}$
,
${\mathbf {c}}_{i,m}\colon (\mathbb {Z}^{L})^{s}\to (\mathbb {Z}^{d})^{L}$
,
![]() $1\leq i\leq k$
,
$1\leq i\leq k$
,
![]() $1\leq m\leq t_{i}$
, with
$1\leq m\leq t_{i}$
, with
![]() ${\mathbf {c}}_{i,m}\not \equiv \mathbf {0},$
such that all the following hold.
${\mathbf {c}}_{i,m}\not \equiv \mathbf {0},$
such that all the following hold.
-
(i) (Control of the coefficients) Each
 ${\mathbf {c}}_{i,m}$
is of the form for some
${\mathbf {c}}_{i,m}$
is of the form for some $$ \begin{align*}{\mathbf{c}}_{i,m}(h_{1},\ldots,h_{s})=\sum_{a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L},\vert a_{1}\vert+\cdots+\vert a_{s}\vert\leq s'}h^{a_{1}}_{1}\cdots h^{a_{s}}_{s}\cdot {\mathbf{v}}_{i,m}(a_{1},\ldots,a_{s})\end{align*} $$
$$ \begin{align*}{\mathbf{c}}_{i,m}(h_{1},\ldots,h_{s})=\sum_{a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L},\vert a_{1}\vert+\cdots+\vert a_{s}\vert\leq s'}h^{a_{1}}_{1}\cdots h^{a_{s}}_{s}\cdot {\mathbf{v}}_{i,m}(a_{1},\ldots,a_{s})\end{align*} $$
 ${\mathbf {v}}_{i,m}(a_{1},\ldots ,a_{s}){\kern-1pt}={\kern-1pt}(v_{i,m,1}(a_{1},\ldots ,a_{s}),\ldots ,v_{i,m,L}(a_{1},\ldots ,a_{s}))\in (\mathbb {Q}^{d})^{L},$
which is a polynomial function in terms of the coefficients of
${\mathbf {v}}_{i,m}(a_{1},\ldots ,a_{s}){\kern-1pt}={\kern-1pt}(v_{i,m,1}(a_{1},\ldots ,a_{s}),\ldots ,v_{i,m,L}(a_{1},\ldots ,a_{s}))\in (\mathbb {Q}^{d})^{L},$
which is a polynomial function in terms of the coefficients of
 $p_{i}, 1\leq i\leq k,$
and whose degree depends only on
$p_{i}, 1\leq i\leq k,$
and whose degree depends only on
 $d,k,K,L$
.
$d,k,K,L$
.
In addition, denoting
we have that each
 $H_{i,m}$
contains one of
$H_{i,m}$
contains one of
 $G_{i,j}(\mathbf {p})$
for some
$G_{i,j}(\mathbf {p})$
for some
 $0\leq j\leq k, j\neq i$
.
$0\leq j\leq k, j\neq i$
.
-
(ii) (Control of the average) For every
 $\mathbb {Z}^{d}$
-system
$\mathbb {Z}^{d}$
-system
 $(X,\mathcal {B},\mu , (T_{g})_{g\in \mathbb {Z}^{d}})$
and every
$(X,\mathcal {B},\mu , (T_{g})_{g\in \mathbb {Z}^{d}})$
and every
 $f_{1},\ldots , f_{k}\in L^{\infty }(\mu )$
bounded by
$f_{1},\ldots , f_{k}\in L^{\infty }(\mu )$
bounded by
 $1,$
we have that (21)
$1,$
we have that (21) $$ \begin{align} &{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\Vert\mathbb{E}_{n\in I_{N}}\prod_{i=1}^k T_{p_{i}(n)}f_i\bigg\Vert^{2^{t_0}}_{2} \notag \\ &\quad \leq C\cdot \min_{1\leq i\leq k}{\overline{\mathbb{E}}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_{i}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{(G'({\mathbf{c}}_{i,m}(h_{1},\ldots,h_{s})))_{1\leq m\leq t_{i}}}, \end{align} $$
$$ \begin{align} &{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\Vert\mathbb{E}_{n\in I_{N}}\prod_{i=1}^k T_{p_{i}(n)}f_i\bigg\Vert^{2^{t_0}}_{2} \notag \\ &\quad \leq C\cdot \min_{1\leq i\leq k}{\overline{\mathbb{E}}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_{i}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{(G'({\mathbf{c}}_{i,m}(h_{1},\ldots,h_{s})))_{1\leq m\leq t_{i}}}, \end{align} $$
where
![]() $t_0$
and
$t_0$
and
![]() $C>0$
are constants depending only on
$C>0$
are constants depending only on
![]() $\mathbf {p}$
.
$\mathbf {p}$
.
Remark 5.6. Both
![]() $t_0$
and C depend on
$t_0$
and C depend on
![]() $d, k, L$
, and the highest degree of
$d, k, L$
, and the highest degree of
![]() $p_{1},\ldots ,p_{k}$
. More specifically,
$p_{1},\ldots ,p_{k}$
. More specifically,
![]() $t_0$
can be chosen to be the maximum number of vdC operations we have to perform, for each
$t_0$
can be chosen to be the maximum number of vdC operations we have to perform, for each
![]() $i,$
for the PET tuple to be non-degenerate,
$i,$
for the PET tuple to be non-degenerate,
![]() $1$
-standard for
$1$
-standard for
![]() $f_i,$
and with degree equal to
$f_i,$
and with degree equal to
![]() $1.$
$1.$
Proposition 5.5 improves on [Reference Donoso, Koutsogiannis and Sun7, Proposition 5.5] as the description of the subgroup
![]() $H_{i,m}$
is much more precise than that of the set
$H_{i,m}$
is much more precise than that of the set
![]() $U_{i,r}(a_{1},\ldots ,a_{s})$
defined in the latter. The rest of this section is devoted to proving Proposition 5.5, which is the most technical result of this paper.
$U_{i,r}(a_{1},\ldots ,a_{s})$
defined in the latter. The rest of this section is devoted to proving Proposition 5.5, which is the most technical result of this paper.
Next, we introduce some convenient notation. Let
![]() $\mathbf {q}=(q_{1},\ldots ,q_{\ell })$
be a tuple of polynomials
$\mathbf {q}=(q_{1},\ldots ,q_{\ell })$
be a tuple of polynomials
![]() $q_{i}\colon ({\mathbb Z}^{L})^{s+1}\to {\mathbb Z}^{d}, 1\leq i\leq \ell ,$
where
$q_{i}\colon ({\mathbb Z}^{L})^{s+1}\to {\mathbb Z}^{d}, 1\leq i\leq \ell ,$
where
 $$ \begin{align*}q_{i}(n;h_{1},\ldots,h_{s})=\sum_{b,a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L}} h^{a_{1}}_{1}\ldots h^{a_{s}}_{s}n^{b}\cdot u_{i}(b;a_{1},\ldots,a_{s})\end{align*} $$
$$ \begin{align*}q_{i}(n;h_{1},\ldots,h_{s})=\sum_{b,a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L}} h^{a_{1}}_{1}\ldots h^{a_{s}}_{s}n^{b}\cdot u_{i}(b;a_{1},\ldots,a_{s})\end{align*} $$
for some
![]() $u_{i}(b;a_{1},\ldots ,a_{s})\in \mathbb {Q}^{d}, 1\leq i\leq \ell $
. Then, by writing
$u_{i}(b;a_{1},\ldots ,a_{s})\in \mathbb {Q}^{d}, 1\leq i\leq \ell $
. Then, by writing
we can express
![]() $\mathbf {q}$
as
$\mathbf {q}$
as
 $$ \begin{align*}\mathbf{q}(n;h_{1},\ldots,h_{s})=\sum_{b,a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L}} h^{a_{1}}_{1}\ldots h^{a_{s}}_{s}n^{b}\cdot \mathbf{u}(b;a_{1},\ldots,a_{s}).\end{align*} $$
$$ \begin{align*}\mathbf{q}(n;h_{1},\ldots,h_{s})=\sum_{b,a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L}} h^{a_{1}}_{1}\ldots h^{a_{s}}_{s}n^{b}\cdot \mathbf{u}(b;a_{1},\ldots,a_{s}).\end{align*} $$
We call
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{d})$
the data of
$\mathbf {u}(b;a_{1},\ldots ,a_{d})$
the data of
![]() $\mathbf {q}$
at level
$\mathbf {q}$
at level
![]() $(b;a_{1},\ldots ,a_{d})$
, or simply the level data of
$(b;a_{1},\ldots ,a_{d})$
, or simply the level data of
![]() $\mathbf {q}$
.
$\mathbf {q}$
.
For the rest of the section, we fix
![]() $d,k,K,L\in \mathbb {N}$
and let
$d,k,K,L\in \mathbb {N}$
and let
![]() $\mathbf {p}=(p_{1},\ldots ,p_{k})$
denote a family of essentially distinct polynomials
$\mathbf {p}=(p_{1},\ldots ,p_{k})$
denote a family of essentially distinct polynomials
![]() $ p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
of degrees at most
$ p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
of degrees at most
![]() $K,$
with
$K,$
with
![]() $p_{i}(n)=\sum _{v\in \mathbb {N}_0^{L}, \vert v\vert \leq K}b_{i,v}n^{v},$
where
$p_{i}(n)=\sum _{v\in \mathbb {N}_0^{L}, \vert v\vert \leq K}b_{i,v}n^{v},$
where
![]() $b_{i,v}\in \mathbb {Q}^{d}$
.
$b_{i,v}\in \mathbb {Q}^{d}$
.
Recalling that
![]() $b_{w,v}$
,
$b_{w,v}$
,
![]() $1\leq w\leq k, v\in {\mathbb N}_0^{L}$
are the coefficients that arise from the family
$1\leq w\leq k, v\in {\mathbb N}_0^{L}$
are the coefficients that arise from the family
![]() $\mathbf {p}$
(we also put
$\mathbf {p}$
(we also put ![]() for all
for all
![]() $v\in {\mathbb N}_0^{L}$
), for
$v\in {\mathbb N}_0^{L}$
), for
![]() $r\in \mathbb {Q}, v\in {\mathbb N}_0^{L}$
, and
$r\in \mathbb {Q}, v\in {\mathbb N}_0^{L}$
, and
![]() $0\leq i\leq k$
, we set
$0\leq i\leq k$
, we set
One sees that the left-hand side of equation (21) is
![]() $S(A,1)$
(recall equation (16) for the definition), where A is the PET-tuple
$S(A,1)$
(recall equation (16) for the definition), where A is the PET-tuple
![]() $(L,0,k,(f_{1},\ldots ,f_{k}),\mathbf {p})$
. To prove Proposition 5.5, we first need to perform a series of vdC operations to convert A into a PET-tuple
$(L,0,k,(f_{1},\ldots ,f_{k}),\mathbf {p})$
. To prove Proposition 5.5, we first need to perform a series of vdC operations to convert A into a PET-tuple
![]() $\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A$
of degree 1, and then compare the coefficients of the polynomials in A with those in
$\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A$
of degree 1, and then compare the coefficients of the polynomials in A with those in
![]() $\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A$
. Even though the coefficients in the latter are very difficult to compute directly, one can keep track of the connection between them and those of the original polynomial family
$\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A$
. Even though the coefficients in the latter are very difficult to compute directly, one can keep track of the connection between them and those of the original polynomial family
![]() $\mathbf {p}$
. This was first achieved in [Reference Donoso, Koutsogiannis and Sun7] by introducing an equivalence relation pertaining to the vdC operation (see [Reference Donoso, Koutsogiannis and Sun7, §5.3] for details). In this paper, we introduce another approach which is more intricate than that used in [Reference Donoso, Koutsogiannis and Sun7], but that achieves a better tracking of the coefficients, which in turn gives us a stronger upper bound for the multiple averages.
$\mathbf {p}$
. This was first achieved in [Reference Donoso, Koutsogiannis and Sun7] by introducing an equivalence relation pertaining to the vdC operation (see [Reference Donoso, Koutsogiannis and Sun7, §5.3] for details). In this paper, we introduce another approach which is more intricate than that used in [Reference Donoso, Koutsogiannis and Sun7], but that achieves a better tracking of the coefficients, which in turn gives us a stronger upper bound for the multiple averages.
Definition 5.7. (Types and symbols of level data)
Fix a tuple
![]() $\mathbf {q}=(q_{1},\ldots ,q_{\ell })$
of polynomials with level data
$\mathbf {q}=(q_{1},\ldots ,q_{\ell })$
of polynomials with level data
![]() $\mathbf {u}$
. For all
$\mathbf {u}$
. For all
![]() $b,a_{1},\ldots ,a_{s},v\in {\mathbb N}_0^{L}$
,
$b,a_{1},\ldots ,a_{s},v\in {\mathbb N}_0^{L}$
,
![]() $r\in \mathbb {Q}$
, and
$r\in \mathbb {Q}$
, and
![]() $0\leq i\leq k$
, we say that
$0\leq i\leq k$
, we say that
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is of type (r,i,v) if
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is of type (r,i,v) if
 $$ \begin{align*} &u_{1}(b;a_{1},\ldots,a_{s}),\ldots,u_{\ell}(b;a_{1},\ldots,a_{s})\in Q_{r,i,v},\quad\text{and}\\ &\qquad\qquad\ \,u_{1}(b;a_{1},\ldots,a_{s}) =r(b_{1,v}-b_{i,v}).\end{align*} $$
$$ \begin{align*} &u_{1}(b;a_{1},\ldots,a_{s}),\ldots,u_{\ell}(b;a_{1},\ldots,a_{s})\in Q_{r,i,v},\quad\text{and}\\ &\qquad\qquad\ \,u_{1}(b;a_{1},\ldots,a_{s}) =r(b_{1,v}-b_{i,v}).\end{align*} $$
We say that
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is non-trivial if at least one of
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is non-trivial if at least one of
![]() $u_{m}(b;a_{1},\ldots ,a_{s})$
is non-zero.
$u_{m}(b;a_{1},\ldots ,a_{s})$
is non-zero.
Let
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
be of type
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
be of type
![]() $(r,i,v)$
. Suppose that
$(r,i,v)$
. Suppose that
for some
![]() $0\leq w_{1},\ldots ,w_{\ell }\leq k$
. We call
$0\leq w_{1},\ldots ,w_{\ell }\leq k$
. We call
![]() $\textsf {w}:=(w_{1},\ldots ,w_{\ell })$
a symbol of
$\textsf {w}:=(w_{1},\ldots ,w_{\ell })$
a symbol of
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
.
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
.
Note that the definition of type and symbol depend on the prefixed polynomial family
![]() $\mathbf {p}$
. Moreover, if
$\mathbf {p}$
. Moreover, if
![]() $(w_{1},\ldots ,w_{\ell })$
is a symbol of
$(w_{1},\ldots ,w_{\ell })$
is a symbol of
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
, then so is
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
, then so is
![]() $(1,w_{2},\ldots ,w_{\ell })$
. We also remark that in the special case
$(1,w_{2},\ldots ,w_{\ell })$
. We also remark that in the special case
![]() $\mathbf {p}=\mathbf {q}$
and
$\mathbf {p}=\mathbf {q}$
and
![]() $s=0$
, all of
$s=0$
, all of
![]() $\mathbf {u}(b;\emptyset )$
are of type
$\mathbf {u}(b;\emptyset )$
are of type
![]() $(1,0,b)$
and have
$(1,0,b)$
and have
![]() $(1,\ldots ,k)$
as a symbol.
$(1,\ldots ,k)$
as a symbol.
We use the types and symbols of level data to track the coefficients of PET-tuples. We start with an example to illustrate this concept.
Example 5.8. Let
![]() $\mathbf {p}=(p_{1},p_{2})$
be defined as in Example 4.7 and let
$\mathbf {p}=(p_{1},p_{2})$
be defined as in Example 4.7 and let
![]() $\mathbf {q}=\partial _{2}\mathbf {p}=(q_{1},q_{2},q_{3})$
(recall that by this, we mean the polynomial iterates we get after running the vdC operation, subtracting the second polynomial,
$\mathbf {q}=\partial _{2}\mathbf {p}=(q_{1},q_{2},q_{3})$
(recall that by this, we mean the polynomial iterates we get after running the vdC operation, subtracting the second polynomial,
![]() $p_2$
). In this case,
$p_2$
). In this case,
 $$ \begin{align*} & \mathbf{u}(0;1)=(b_{1,1},b_{2,1},0) \text{ is of type }(1,0,1)\text{ and has symbol }(1,2,0), \\& \mathbf{u}(0;2)=(b_{1,2},b_{2,2},0) \text{ is of type }(1,0,2)\text{ and has symbol }(1,2,0), \\& \mathbf{u}(1;0)=(b_{1,1}-b_{2,1},0,b_{1,1}-b_{2,1}) \text{ is of type }(1,2,1)\text{ and has symbol }(1,2,1), \\& \mathbf{u}(1;1)=(2b_{1,2},2b_{2,2},0) \text{ is of type }(2,0,2)\text{ and has symbol }(1,2,0), \\& \mathbf{u}(2;0)=(b_{1,2}-b_{2,2},0,b_{1,2}-b_{2,2}) \text{ is of type }(1,2,2)\text{ and has symbol }(1,2,1). \end{align*} $$
$$ \begin{align*} & \mathbf{u}(0;1)=(b_{1,1},b_{2,1},0) \text{ is of type }(1,0,1)\text{ and has symbol }(1,2,0), \\& \mathbf{u}(0;2)=(b_{1,2},b_{2,2},0) \text{ is of type }(1,0,2)\text{ and has symbol }(1,2,0), \\& \mathbf{u}(1;0)=(b_{1,1}-b_{2,1},0,b_{1,1}-b_{2,1}) \text{ is of type }(1,2,1)\text{ and has symbol }(1,2,1), \\& \mathbf{u}(1;1)=(2b_{1,2},2b_{2,2},0) \text{ is of type }(2,0,2)\text{ and has symbol }(1,2,0), \\& \mathbf{u}(2;0)=(b_{1,2}-b_{2,2},0,b_{1,2}-b_{2,2}) \text{ is of type }(1,2,2)\text{ and has symbol }(1,2,1). \end{align*} $$
Definition 5.9. Let S denote the set of all
![]() $(a,a')\in {\mathbb N}_0^{ 2L}$
such that a and
$(a,a')\in {\mathbb N}_0^{ 2L}$
such that a and
![]() $a'$
are both
$a'$
are both
![]() $\mathbf {0}$
or both different than
$\mathbf {0}$
or both different than
![]() $\mathbf {0}$
. Let
$\mathbf {0}$
. Let
![]() $\mathbf {q}$
be a polynomial family of degree at least 1. We say that
$\mathbf {q}$
be a polynomial family of degree at least 1. We say that
![]() $\mathbf {q}$
satisfies properties (P1)–(P4) if its level data
$\mathbf {q}$
satisfies properties (P1)–(P4) if its level data
![]() $\mathbf {u}$
satisfy the following conditions.
$\mathbf {u}$
satisfy the following conditions.
(P1) For all
![]() $a_{1},\ldots ,a_{s},b$
, there exist
$a_{1},\ldots ,a_{s},b$
, there exist
![]() $r,i,v$
such that
$r,i,v$
such that
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is of type
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is of type
![]() $(r,i,v)$
. Moreover, we may choose the type and symbol for all of
$(r,i,v)$
. Moreover, we may choose the type and symbol for all of
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
in a way such that (P2)–(P4) hold.
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
in a way such that (P2)–(P4) hold.
(P2) If
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is of type
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is of type
![]() $(r,i,v)$
, then
$(r,i,v)$
, then
![]() $r=\binom {b+a_{1}+\cdots +a_{s}}{a_{1},\ldots ,a_{s}}$
and
$r=\binom {b+a_{1}+\cdots +a_{s}}{a_{1},\ldots ,a_{s}}$
and
![]() $v=b+a_{1}+\cdots +a_{s}$
(in particular,
$v=b+a_{1}+\cdots +a_{s}$
(in particular,
![]() $r\neq 0$
, where, for
$r\neq 0$
, where, for
![]() $v_{i}=(v_{i,1},\ldots ,v_{i,L})\in {\mathbb N}_0^{L}, 1\leq i\leq s$
, we denote
$v_{i}=(v_{i,1},\ldots ,v_{i,L})\in {\mathbb N}_0^{L}, 1\leq i\leq s$
, we denote ![]() ).
).
(P3) Suppose that
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is of type
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is of type
![]() $(r,i,v)$
and
$(r,i,v)$
and
![]() $\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
is of type
$\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
is of type
![]() $(r',i',v')$
. If
$(r',i',v')$
. If
![]() $(a_{1},a^{\prime}_{1}),\ldots ,(a_{s},a^{\prime}_{s})\in S$
, then
$(a_{1},a^{\prime}_{1}),\ldots ,(a_{s},a^{\prime}_{s})\in S$
, then
![]() $i=i'$
and
$i=i'$
and
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s}), \mathbf {u}(b';a^{\prime}_{1},\ldots , a^{\prime}_{s})$
share a symbol.
$\mathbf {u}(b;a_{1},\ldots ,a_{s}), \mathbf {u}(b';a^{\prime}_{1},\ldots , a^{\prime}_{s})$
share a symbol.
(P4) For every
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
, the first coordinate
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
, the first coordinate
![]() $w_{1}$
of its symbol
$w_{1}$
of its symbol
![]() $(w_{1},\ldots ,w_{\ell })$
equals to 1.
$(w_{1},\ldots ,w_{\ell })$
equals to 1.
For convenience, we say that a PET-tuple
![]() $A=(L,s,\ell ,\mathbf {g},\mathbf {q})$
satisfies properties (P1)–(P4) if the polynomial family
$A=(L,s,\ell ,\mathbf {g},\mathbf {q})$
satisfies properties (P1)–(P4) if the polynomial family
![]() $\mathbf {q}$
associated to A satisfies properties (P1)–(P4).
$\mathbf {q}$
associated to A satisfies properties (P1)–(P4).
Once again, properties (P1)–(P4) are taken with respect to the prefixed polynomial family
![]() $\mathbf {p}.$
It is obvious that
$\mathbf {p}.$
It is obvious that
![]() $\mathbf {p}$
itself satisfies properties (P1)–(P4). An important feature of the type and symbol of level data is that properties (P1)–(P4) are preserved under vdC operations.
$\mathbf {p}$
itself satisfies properties (P1)–(P4). An important feature of the type and symbol of level data is that properties (P1)–(P4) are preserved under vdC operations.
Example 5.10. We will verify that the polynomial family
![]() $\mathbf {q}=\partial _{2}\mathbf {p}$
in Example 5.8 satisfies all of the properties (P1)–(P4). Indeed, property (P1) holds as all
$\mathbf {q}=\partial _{2}\mathbf {p}$
in Example 5.8 satisfies all of the properties (P1)–(P4). Indeed, property (P1) holds as all
![]() $\mathbf {u}(0;1), \mathbf {u}(0;2),\mathbf {u}(1;0),\mathbf {u}(1;1),\mathbf {u}(2;0)$
have a type. For all
$\mathbf {u}(0;1), \mathbf {u}(0;2),\mathbf {u}(1;0),\mathbf {u}(1;1),\mathbf {u}(2;0)$
have a type. For all
![]() $0\leq a,b\leq 2, a+b\leq 2$
, if
$0\leq a,b\leq 2, a+b\leq 2$
, if
![]() $\mathbf {u}(b;a)$
is of type
$\mathbf {u}(b;a)$
is of type
![]() $(r,i,v)$
, then it is not hard to see that
$(r,i,v)$
, then it is not hard to see that
![]() $r=\binom {b+a}{a}$
, so property (P2) holds. Property (P3) can be verified by comparing the types and symbols of the pairs
$r=\binom {b+a}{a}$
, so property (P2) holds. Property (P3) can be verified by comparing the types and symbols of the pairs
![]() $(\mathbf {u}(0,1),\mathbf {u}(0,2))$
and
$(\mathbf {u}(0,1),\mathbf {u}(0,2))$
and
![]() $(\mathbf {u}(1,0),\mathbf {u}(2,0))$
. Finally, property (P4) also holds since the first entry of every symbol in
$(\mathbf {u}(1,0),\mathbf {u}(2,0))$
. Finally, property (P4) also holds since the first entry of every symbol in
![]() $\mathbf {q}$
is 1.
$\mathbf {q}$
is 1.
We caution the reader that the symbol and type may not be unique if the coefficients
![]() $b_{i,v}$
satisfy some algebraic relations. For example, in Example 5.8, if
$b_{i,v}$
satisfy some algebraic relations. For example, in Example 5.8, if
![]() $b_{1,1}=b_{2,1}$
, then both
$b_{1,1}=b_{2,1}$
, then both
![]() $(1,2,0)$
and
$(1,2,0)$
and
![]() $(1,1,0)$
are symbols of
$(1,1,0)$
are symbols of
![]() $\mathbf {u}(0;1)=(b_{1,1},b_{2,1},0)$
. However, the following result says that there is always a way to choose symbols and types so that properties (P1)–(P4) are preserved under vdC operations.
$\mathbf {u}(0;1)=(b_{1,1},b_{2,1},0)$
. However, the following result says that there is always a way to choose symbols and types so that properties (P1)–(P4) are preserved under vdC operations.
Proposition 5.11. Let
![]() $A=(L,s,\ell ,\mathbf {g},\mathbf {q})$
be a non-degenerate PET-tuple and
$A=(L,s,\ell ,\mathbf {g},\mathbf {q})$
be a non-degenerate PET-tuple and
![]() $1\leq \rho \leq \ell $
. Assume that
$1\leq \rho \leq \ell $
. Assume that
![]() $A\to \partial _{\rho }A$
is 1-inherited. If A satisfies properties (P1)–(P4), then
$A\to \partial _{\rho }A$
is 1-inherited. If A satisfies properties (P1)–(P4), then
![]() $\partial _{\rho }A$
also satisfies properties (P1)–(P4).
$\partial _{\rho }A$
also satisfies properties (P1)–(P4).
Proof. Suppose that
![]() $\mathbf {q}=(q_{1},\ldots ,q_{\ell })$
. Denote
$\mathbf {q}=(q_{1},\ldots ,q_{\ell })$
. Denote
![]() $\mathbf {q}^{\ast }=(q^{\ast }_{1},\ldots ,q^{\ast }_{2\ell })$
, where for all
$\mathbf {q}^{\ast }=(q^{\ast }_{1},\ldots ,q^{\ast }_{2\ell })$
, where for all
![]() $1\leq i\leq ~\ell ,$
$1\leq i\leq ~\ell ,$
and
Assuming that
 $$ \begin{align*}q_{i}(n;h_{1},\ldots,h_{s})=\sum_{b,a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L}} h^{a_{1}}_{1}\cdots h^{a_{s}}_{s}n^{b}\cdot u_{i}(b;a_{1},\ldots,a_{s})\end{align*} $$
$$ \begin{align*}q_{i}(n;h_{1},\ldots,h_{s})=\sum_{b,a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L}} h^{a_{1}}_{1}\cdots h^{a_{s}}_{s}n^{b}\cdot u_{i}(b;a_{1},\ldots,a_{s})\end{align*} $$
for all
![]() $1\leq i\leq \ell ,$
we may write
$1\leq i\leq \ell ,$
we may write
![]() $\mathbf {q}$
as
$\mathbf {q}$
as
 $$ \begin{align*}\mathbf{q}(n;h_{1},\ldots,h_{s})=\sum_{b,a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L}} h^{a_{1}}_{1}\cdots h^{a_{s}}_{s}n^{b}\cdot \mathbf{u}(b;a_{1},\ldots,a_{s}),\end{align*} $$
$$ \begin{align*}\mathbf{q}(n;h_{1},\ldots,h_{s})=\sum_{b,a_{1},\ldots,a_{s}\in\mathbb{N}_0^{L}} h^{a_{1}}_{1}\cdots h^{a_{s}}_{s}n^{b}\cdot \mathbf{u}(b;a_{1},\ldots,a_{s}),\end{align*} $$
and define
![]() $\mathbf {u}^{\ast }(b;a_{1},\ldots ,a_{s+1})$
in a similar way.
$\mathbf {u}^{\ast }(b;a_{1},\ldots ,a_{s+1})$
in a similar way.
One can immediately check that
 $$ \begin{align*} &q_{i}(n+h_{s+1};h_{1},\ldots,h_{s}) \\ &\quad=\sum_{b,a_{1},\ldots,a_{s+1}\in\mathbb{N}_0^{L}} h^{a_{1}}_{1}\cdots h^{a_{s+1}}_{s+1}n^{b}\cdot \binom{b+a_{s+1}}{b}u_{i}(b+a_{s+1};a_{1},\ldots,a_{s}).\end{align*} $$
$$ \begin{align*} &q_{i}(n+h_{s+1};h_{1},\ldots,h_{s}) \\ &\quad=\sum_{b,a_{1},\ldots,a_{s+1}\in\mathbb{N}_0^{L}} h^{a_{1}}_{1}\cdots h^{a_{s+1}}_{s+1}n^{b}\cdot \binom{b+a_{s+1}}{b}u_{i}(b+a_{s+1};a_{1},\ldots,a_{s}).\end{align*} $$
(For
![]() $a=(a_{1},\ldots ,a_{L}), b=(b_{1},\ldots ,b_{L})\in \mathbb {N}_0^{L}$
,
$a=(a_{1},\ldots ,a_{L}), b=(b_{1},\ldots ,b_{L})\in \mathbb {N}_0^{L}$
,
![]() $\binom {a}{b}$
denotes the quantity
$\binom {a}{b}$
denotes the quantity
![]() $\prod _{m=1}^{L}\binom {a_{m}}{b_{m}}$
.) Then,
$\prod _{m=1}^{L}\binom {a_{m}}{b_{m}}$
.) Then,
 $$ \begin{align} u^{\ast}_{i}(b;a_{1},\ldots,a_{s+1})=\left\{ \begin{aligned} &u_{i}(b;a_{1},\ldots,a_{s})-u_{\rho}(b;a_{1},\ldots,a_{s}), & & a_{s+1}=\mathbf{0}, \\ &\binom{b+a_{s+1}}{b}u_{i}(b+a_{s+1};a_{1},\ldots,a_{s}), & & a_{s+1}\neq \mathbf{0}, \end{aligned} \right. \end{align} $$
$$ \begin{align} u^{\ast}_{i}(b;a_{1},\ldots,a_{s+1})=\left\{ \begin{aligned} &u_{i}(b;a_{1},\ldots,a_{s})-u_{\rho}(b;a_{1},\ldots,a_{s}), & & a_{s+1}=\mathbf{0}, \\ &\binom{b+a_{s+1}}{b}u_{i}(b+a_{s+1};a_{1},\ldots,a_{s}), & & a_{s+1}\neq \mathbf{0}, \end{aligned} \right. \end{align} $$
and
 $$ \begin{align} u^{\ast}_{i+\ell}(b;a_{1},\ldots,a_{s+1})=\left\{ \begin{aligned} &u_{i}(b;a_{1},\ldots,a_{s})-u_{\rho}(b;a_{1},\ldots,a_{s}), & & a_{s+1}=\mathbf{0}, \\ &\mathbf{0}, & & a_{s+1}\neq \mathbf{0}. \end{aligned} \right. \end{align} $$
$$ \begin{align} u^{\ast}_{i+\ell}(b;a_{1},\ldots,a_{s+1})=\left\{ \begin{aligned} &u_{i}(b;a_{1},\ldots,a_{s})-u_{\rho}(b;a_{1},\ldots,a_{s}), & & a_{s+1}=\mathbf{0}, \\ &\mathbf{0}, & & a_{s+1}\neq \mathbf{0}. \end{aligned} \right. \end{align} $$
We first show that
![]() $\mathbf {q}$
satisfying properties (P1)–(P4) implies the same for
$\mathbf {q}$
satisfying properties (P1)–(P4) implies the same for
![]() $\mathbf {q}^{\ast }$
.
$\mathbf {q}^{\ast }$
.
Since
![]() $\mathbf {q}$
satisfies property (P1), for all
$\mathbf {q}$
satisfies property (P1), for all
![]() $(b;a_{1},\ldots ,a_{s})$
, there exists a choice of type
$(b;a_{1},\ldots ,a_{s})$
, there exists a choice of type
and symbol
such that properties (P2)–(P4) hold. By property (P2), we have that
 $$ \begin{align} r(b;a_{1},\ldots,a_{s})=\binom{b+a_{1}+\cdots+a_{s}}{a_{1},\ldots,a_{s}} \text{ and } v(b;a_{1},\ldots,a_{s})=b+a_{1}+\cdots+a_{s}. \end{align} $$
$$ \begin{align} r(b;a_{1},\ldots,a_{s})=\binom{b+a_{1}+\cdots+a_{s}}{a_{1},\ldots,a_{s}} \text{ and } v(b;a_{1},\ldots,a_{s})=b+a_{1}+\cdots+a_{s}. \end{align} $$
By property (P4),
![]() $w_{1}(b;a_{1},\ldots ,a_{s})=1$
. We have that
$w_{1}(b;a_{1},\ldots ,a_{s})=1$
. We have that
From now on, we fix some
![]() $b,a_{1},\ldots ,a_{s+1}$
and denote
$b,a_{1},\ldots ,a_{s+1}$
and denote
![]() $\mathbf {x}:=(b+a_{s+1};a_{1},\ldots ,a_{s})$
. By equations (22), (23), and (25), it is not hard to see that
$\mathbf {x}:=(b+a_{s+1};a_{1},\ldots ,a_{s})$
. By equations (22), (23), and (25), it is not hard to see that
![]() $\mathbf {u}^{\ast }(b;a_{1},\ldots ,a_{s},a_{s+1})$
is
$\mathbf {u}^{\ast }(b;a_{1},\ldots ,a_{s},a_{s+1})$
is
 $$ \begin{align} \left\{ \begin{aligned} &\text{of type }(r(\mathbf{x}),w_{\rho}(\mathbf{x}),v(\mathbf{x}))\text{ and has symbol }(\textsf{w}(\mathbf{x}),\textsf{w}(\mathbf{x})), & & a_{s+1}=\mathbf{0}, \\ &\text{of type }(r(\mathbf{x})\binom{b+a_{s+1}}{b},i(\mathbf{x}),v(\mathbf{x}))\text{ and has symbol }(\textsf{w}(\mathbf{x}),i,\ldots,i), & & a_{s+1}\neq \mathbf{0}. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\text{of type }(r(\mathbf{x}),w_{\rho}(\mathbf{x}),v(\mathbf{x}))\text{ and has symbol }(\textsf{w}(\mathbf{x}),\textsf{w}(\mathbf{x})), & & a_{s+1}=\mathbf{0}, \\ &\text{of type }(r(\mathbf{x})\binom{b+a_{s+1}}{b},i(\mathbf{x}),v(\mathbf{x}))\text{ and has symbol }(\textsf{w}(\mathbf{x}),i,\ldots,i), & & a_{s+1}\neq \mathbf{0}. \end{aligned} \right. \end{align} $$
So, each
![]() $\mathbf {u}^{\ast }(b;a_{1},\ldots ,a_{s},a_{s+1})$
has a choice of type and symbol given by equation (26). So
$\mathbf {u}^{\ast }(b;a_{1},\ldots ,a_{s},a_{s+1})$
has a choice of type and symbol given by equation (26). So
![]() $\mathbf {q}^{\ast }$
satisfies property (P1). It suffices to show that the type and symbol given by equation (26) satisfies properties (P2)–(P4).
$\mathbf {q}^{\ast }$
satisfies property (P1). It suffices to show that the type and symbol given by equation (26) satisfies properties (P2)–(P4).
To check property (P2) for
![]() $\mathbf {q}^{\ast }$
, suppose that
$\mathbf {q}^{\ast }$
, suppose that
![]() $\mathbf {u}^{\ast }(b;a_{1},\ldots ,a_{s+1})$
is of type
$\mathbf {u}^{\ast }(b;a_{1},\ldots ,a_{s+1})$
is of type
![]() $(r,i,v)$
. By equation (26), we have that
$(r,i,v)$
. By equation (26), we have that
![]() $\mathbf {u}(b+a_{s+1};a_{1},\ldots ,a_{s})$
is of type
$\mathbf {u}(b+a_{s+1};a_{1},\ldots ,a_{s})$
is of type
![]() $(r\binom {b+a_{s+1}}{b}^{-1},i',v)=(r(\mathbf {x}),i(\mathbf {x}),v(\mathbf {x}))$
for some
$(r\binom {b+a_{s+1}}{b}^{-1},i',v)=(r(\mathbf {x}),i(\mathbf {x}),v(\mathbf {x}))$
for some
![]() $i'$
. Since
$i'$
. Since
![]() $\mathbf {q}$
satisfies property (P2), we have the same for
$\mathbf {q}$
satisfies property (P2), we have the same for
![]() $\mathbf {q}^{\ast }$
as it follows from equation (24) that
$\mathbf {q}^{\ast }$
as it follows from equation (24) that
 $$ \begin{align*}r=\binom{b+a_{s+1}}{b}\binom{(b+a_{s+1})+a_{1}+\cdots+a_{s}}{a_{1},\ldots,a_{s}}=\binom{b+a_{1}+\cdots+a_{s+1}}{a_{1},\ldots,a_{s+1}}\end{align*} $$
$$ \begin{align*}r=\binom{b+a_{s+1}}{b}\binom{(b+a_{s+1})+a_{1}+\cdots+a_{s}}{a_{1},\ldots,a_{s}}=\binom{b+a_{1}+\cdots+a_{s+1}}{a_{1},\ldots,a_{s+1}}\end{align*} $$
and
To show property (P3), pick any
![]() $b',a^{\prime}_{1},\ldots ,a^{\prime}_{s+1}$
with
$b',a^{\prime}_{1},\ldots ,a^{\prime}_{s+1}$
with
![]() $(a_{1},a^{\prime}_{1}),\ldots ,(a_{s+1}, a^{\prime}_{s+1})\in S$
. For convenience, denote
$(a_{1},a^{\prime}_{1}),\ldots ,(a_{s+1}, a^{\prime}_{s+1})\in S$
. For convenience, denote
![]() $\mathbf {x}':=(b'+a^{\prime}_{s+1};a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
. Since
$\mathbf {x}':=(b'+a^{\prime}_{s+1};a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
. Since
![]() $\mathbf {q}$
satisfies property (P3), we have that
$\mathbf {q}$
satisfies property (P3), we have that
![]() $i(\mathbf {x}){\kern-1pt}={\kern-1pt}i(\mathbf {x}')$
and that
$i(\mathbf {x}){\kern-1pt}={\kern-1pt}i(\mathbf {x}')$
and that
![]() $w(\mathbf {x}){\kern-1pt}={\kern-1pt}w'(\mathbf {x}')$
. Since
$w(\mathbf {x}){\kern-1pt}={\kern-1pt}w'(\mathbf {x}')$
. Since
![]() $(a_{s+1},a^{\prime}_{s+1})\in S$
, by equation (26), we have that
$(a_{s+1},a^{\prime}_{s+1})\in S$
, by equation (26), we have that
![]() $\mathbf {q}^{\ast }$
satisfies property (P3).
$\mathbf {q}^{\ast }$
satisfies property (P3).
Finally, it is straightforward from equation (26) that property (P4) is also heritable.
Since the polynomials in
![]() $\partial _{\rho }A$
are obtained by removing some terms from the tuple
$\partial _{\rho }A$
are obtained by removing some terms from the tuple
![]() $\mathbf {q}^{\ast }$
(but not the first one as
$\mathbf {q}^{\ast }$
(but not the first one as
![]() $A\to \partial _{\rho } A$
is 1-inherited), the fact that
$A\to \partial _{\rho } A$
is 1-inherited), the fact that
![]() $\mathbf {q}^{\ast }$
satisfies properties (P1)–(P4) implies that
$\mathbf {q}^{\ast }$
satisfies properties (P1)–(P4) implies that
![]() $\partial _{\rho }A$
also satisfies properties (P1)–(P4).
$\partial _{\rho }A$
also satisfies properties (P1)–(P4).
For the family of essentially distinct polynomials
![]() $\mathbf {p}=(p_{1},\ldots ,p_{k}),$
Proposition 5.11 implies that
$\mathbf {p}=(p_{1},\ldots ,p_{k}),$
Proposition 5.11 implies that
![]() $\partial _{i_{k}}\ldots \partial _{i_{1}}\mathbf {p}$
satisfies properties (P1)–(P4) for all
$\partial _{i_{k}}\ldots \partial _{i_{1}}\mathbf {p}$
satisfies properties (P1)–(P4) for all
![]() $k,i_{1},\ldots ,i_{k}\in {\mathbb N}$
. In the special case when
$k,i_{1},\ldots ,i_{k}\in {\mathbb N}$
. In the special case when
![]() $\partial _{i_{k}}\ldots \partial _{i_{1}}\mathbf {p}$
is of degree 1, properties (P1)–(P4) provide us with some information on the seminorm we use to bound
$\partial _{i_{k}}\ldots \partial _{i_{1}}\mathbf {p}$
is of degree 1, properties (P1)–(P4) provide us with some information on the seminorm we use to bound
![]() $S(\partial _{i_{k}}\ldots \partial _{i_{1}}A,1)$
. To be more precise, if properties (P1)–(P4) hold for some non-degenerate
$S(\partial _{i_{k}}\ldots \partial _{i_{1}}A,1)$
. To be more precise, if properties (P1)–(P4) hold for some non-degenerate
![]() $\mathbf {q}$
, then there is some connection between the level data of
$\mathbf {q}$
, then there is some connection between the level data of
![]() $\mathbf {q}$
and the groups
$\mathbf {q}$
and the groups
![]() $G_{1,0}(\mathbf {p}),G_{1,2}(\mathbf {p}),\ldots ,G_{1,k}(\mathbf {p})$
.
$G_{1,0}(\mathbf {p}),G_{1,2}(\mathbf {p}),\ldots ,G_{1,k}(\mathbf {p})$
.
Proposition 5.12. Suppose that properties (P1)–(P4) hold for some non-degenerate
![]() $\mathbf {q}$
. Then for all
$\mathbf {q}$
. Then for all
![]() $0\leq m\leq \ell , m\neq 1$
, the group
$0\leq m\leq \ell , m\neq 1$
, the group

contains at least one of the groups
![]() $G_{1,j}(\mathbf {p}), 0\leq j\leq k, j\neq 1$
.
$G_{1,j}(\mathbf {p}), 0\leq j\leq k, j\neq 1$
.
We remark that although Proposition 5.12 holds for all non-degenerate
![]() $\mathbf {q}$
, we will use it for the case
$\mathbf {q}$
, we will use it for the case
![]() $\deg (\mathbf {q})=1$
. We first give an example to explain the idea behind it.
$\deg (\mathbf {q})=1$
. We first give an example to explain the idea behind it.
Example 5.13. Let
![]() $\mathbf {p}=(p_{1},p_{2})$
be as in Example 4.7. Then,
$\mathbf {p}=(p_{1},p_{2})$
be as in Example 4.7. Then,
![]() $G_{1,0}(\mathbf {p})=G(b_{1,2})$
and
$G_{1,0}(\mathbf {p})=G(b_{1,2})$
and
![]() $G_{1,2}(\mathbf {p})=G(b_{1,2}-b_{2,2})$
. Let
$G_{1,2}(\mathbf {p})=G(b_{1,2}-b_{2,2})$
. Let
![]() $\mathbf {u}(b;a)$
be the level data of
$\mathbf {u}(b;a)$
be the level data of
![]() $\partial _{2}\mathbf {p}$
. Then,
$\partial _{2}\mathbf {p}$
. Then,
 $$ \begin{align*}\nonumber & \mathbf{u}(1;0)=(b_{1,1}-b_{2,1})\cdot(1,0,1) \text{ is of type }(1,2,1)\text{ and has symbol }(1,2,1), \\& \mathbf{u}(1;1)=2b_{1,2}\cdot(1,0,0)+2b_{2,2}\cdot(0,1,0) \text{ is of type }(2,0,2)\text{ and has symbol }(1,2,0), \\& \mathbf{u}(2;0)=(b_{1,2}-b_{2,2})\cdot(1,0,1) \text{ is of type }(1,2,2)\text{ and has symbol }(1,2,1). \end{align*} $$
$$ \begin{align*}\nonumber & \mathbf{u}(1;0)=(b_{1,1}-b_{2,1})\cdot(1,0,1) \text{ is of type }(1,2,1)\text{ and has symbol }(1,2,1), \\& \mathbf{u}(1;1)=2b_{1,2}\cdot(1,0,0)+2b_{2,2}\cdot(0,1,0) \text{ is of type }(2,0,2)\text{ and has symbol }(1,2,0), \\& \mathbf{u}(2;0)=(b_{1,2}-b_{2,2})\cdot(1,0,1) \text{ is of type }(1,2,2)\text{ and has symbol }(1,2,1). \end{align*} $$
Here, we will not compute
![]() $\mathbf {u}(b;a)$
for
$\mathbf {u}(b;a)$
for
![]() $b=0$
as it is irrelevant to our purposes. It is easy to see that
$b=0$
as it is irrelevant to our purposes. It is easy to see that
![]() $H_{1,0}(\partial _{2}\mathbf {p})=G(b_{1,1}-b_{2,1},b_{1,2},b_{1,2}-b_{2,2})\supseteq G_{1,0}(\mathbf {p})\cup G_{1,2}(\mathbf {p})$
,
$H_{1,0}(\partial _{2}\mathbf {p})=G(b_{1,1}-b_{2,1},b_{1,2},b_{1,2}-b_{2,2})\supseteq G_{1,0}(\mathbf {p})\cup G_{1,2}(\mathbf {p})$
,
![]() $H_{1,2}(\partial _{2}\mathbf {p})=G(b_{1,1}-b_{2,1},b_{1,2}-b_{2,2})\supseteq G_{1,2}(\mathbf {p})$
,
$H_{1,2}(\partial _{2}\mathbf {p})=G(b_{1,1}-b_{2,1},b_{1,2}-b_{2,2})\supseteq G_{1,2}(\mathbf {p})$
,
![]() $H_{1,3}(\partial _{2}\mathbf {p})=G(b_{1,2})=G_{1,0}(\mathbf {p})$
. So, Proposition 5.12 holds for
$H_{1,3}(\partial _{2}\mathbf {p})=G(b_{1,2})=G_{1,0}(\mathbf {p})$
. So, Proposition 5.12 holds for
![]() $\partial _{2}\mathbf {p}$
.
$\partial _{2}\mathbf {p}$
.
Let
![]() $\mathbf {u}'(b;a_{1},a_{2})$
denote the level data of
$\mathbf {u}'(b;a_{1},a_{2})$
denote the level data of
![]() $\partial _{2}\partial _{2}\mathbf {p}$
. Then,
$\partial _{2}\partial _{2}\mathbf {p}$
. Then,
 $$ \begin{align*}\nonumber \mathbf{u}'(1;0,0)&=(b_{1,1}-b_{2,1})\cdot(1,1,1,1) \text{ is of type }(1,2,1)\text{ and has symbol }(1,1,1,1), \\ \mathbf{u}'(1;1,0)&=2(b_{1,2}-b_{2,2})\cdot(1,0,1,0) -2b_{2,2}\cdot(0,1,0,1)\\ &\quad \text{ is of type }(2,2,2)\text{ and has symbol}\ (1,0,1,0), \\ \mathbf{u}'(1;0,1)&=2(b_{1,2}-b_{2,2})\cdot(1,1,0,0) \text{ is of type }(2,2,2)\text{ and has symbol }(1,1,2,2), \\ \mathbf{u}'(2;0,0)&=(b_{1,2}-b_{2,2})\cdot(1,1,1,1) \text{ is of type }(1,2,2)\text{ and has symbol }(1,1,1,1). \end{align*} $$
$$ \begin{align*}\nonumber \mathbf{u}'(1;0,0)&=(b_{1,1}-b_{2,1})\cdot(1,1,1,1) \text{ is of type }(1,2,1)\text{ and has symbol }(1,1,1,1), \\ \mathbf{u}'(1;1,0)&=2(b_{1,2}-b_{2,2})\cdot(1,0,1,0) -2b_{2,2}\cdot(0,1,0,1)\\ &\quad \text{ is of type }(2,2,2)\text{ and has symbol}\ (1,0,1,0), \\ \mathbf{u}'(1;0,1)&=2(b_{1,2}-b_{2,2})\cdot(1,1,0,0) \text{ is of type }(2,2,2)\text{ and has symbol }(1,1,2,2), \\ \mathbf{u}'(2;0,0)&=(b_{1,2}-b_{2,2})\cdot(1,1,1,1) \text{ is of type }(1,2,2)\text{ and has symbol }(1,1,1,1). \end{align*} $$
(We do not compute the types and symbols for
![]() $\mathbf {u}'(b;a_{1},a_{2})$
for
$\mathbf {u}'(b;a_{1},a_{2})$
for
![]() $b=0$
.) It is easy to see that
$b=0$
.) It is easy to see that
![]() $H_{1,0}(\partial _{2}\partial _{2}\mathbf {p})=G(b_{1,1}-b_{2,1},b_{1,2}-b_{2,2})\supseteq G_{1,2}(\mathbf {p})$
,
$H_{1,0}(\partial _{2}\partial _{2}\mathbf {p})=G(b_{1,1}-b_{2,1},b_{1,2}-b_{2,2})\supseteq G_{1,2}(\mathbf {p})$
,
![]() $H_{1,2}(\partial _{2}\partial _{2}\mathbf {p})=G(b_{1,2})= G_{1,0}(\mathbf {p}), H_{1,3}(\partial _{2}\partial _{2}\mathbf {p})\ {=}\ G(b_{1,2}-b_{2,2})\ {\supseteq}\ G_{1,2}(\mathbf {p}), H_{1,4}(\partial _{2}\partial _{2}\mathbf {p})\ {=}\ G(b_{1,2},b_{1,2}-b_{2,2})\,{\supseteq} G_{1,0}(\mathbf {p})\cup G_{1,2}(\mathbf {p})$
. So, Proposition 5.12 holds for
$H_{1,2}(\partial _{2}\partial _{2}\mathbf {p})=G(b_{1,2})= G_{1,0}(\mathbf {p}), H_{1,3}(\partial _{2}\partial _{2}\mathbf {p})\ {=}\ G(b_{1,2}-b_{2,2})\ {\supseteq}\ G_{1,2}(\mathbf {p}), H_{1,4}(\partial _{2}\partial _{2}\mathbf {p})\ {=}\ G(b_{1,2},b_{1,2}-b_{2,2})\,{\supseteq} G_{1,0}(\mathbf {p})\cup G_{1,2}(\mathbf {p})$
. So, Proposition 5.12 holds for
![]() $\partial _{2}\partial _{2}\mathbf {p}$
.
$\partial _{2}\partial _{2}\mathbf {p}$
.
Finally, let
![]() $\mathbf {u}''(b;a_{1},a_{2},a_{3})$
denote the level data of
$\mathbf {u}''(b;a_{1},a_{2},a_{3})$
denote the level data of
![]() $\partial _{4}\partial _{2}\partial _{2}\mathbf {p}$
. Then,
$\partial _{4}\partial _{2}\partial _{2}\mathbf {p}$
. Then,
![]() $\deg (\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=1$
and
$\deg (\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=1$
and
 $$ \begin{align*}\nonumber \mathbf{u}''(1;0,0,0) &=(0,0,0,0,0,0,0) \text{ is trivial}, \\ \mathbf{u}''(1;1,0,0) &=2b_{1,2}\cdot(1,0,1,0,1,0,1) \\ &\quad\text{ is of type }(2,0,2)\text{ and has symbol }(1,0,1,0,1,0,1), \\ \mathbf{u}''(1;0,1,0) &=2(b_{1,2}-b_{2,2})\cdot(1,1,0,0,1,1,0)\\ &\quad \text{ is of type }(2,2,2)\text{ and has symbol }(1,1,2,2,1,1,2), \\ \mathbf{u}''(1;0,0,1) &=2(b_{1,2}-b_{2,2})\cdot(1,1,1,1,0,0,0) \\ &\quad\text{ is of type }(2,2,2)\text{ and has symbol }(1,1,1,1,2,2,2). \end{align*} $$
$$ \begin{align*}\nonumber \mathbf{u}''(1;0,0,0) &=(0,0,0,0,0,0,0) \text{ is trivial}, \\ \mathbf{u}''(1;1,0,0) &=2b_{1,2}\cdot(1,0,1,0,1,0,1) \\ &\quad\text{ is of type }(2,0,2)\text{ and has symbol }(1,0,1,0,1,0,1), \\ \mathbf{u}''(1;0,1,0) &=2(b_{1,2}-b_{2,2})\cdot(1,1,0,0,1,1,0)\\ &\quad \text{ is of type }(2,2,2)\text{ and has symbol }(1,1,2,2,1,1,2), \\ \mathbf{u}''(1;0,0,1) &=2(b_{1,2}-b_{2,2})\cdot(1,1,1,1,0,0,0) \\ &\quad\text{ is of type }(2,2,2)\text{ and has symbol }(1,1,1,1,2,2,2). \end{align*} $$
(Once more, we do not compute the types and symbols for
![]() $\mathbf {u}''(b;a_{1},a_{2},a_{3})$
for
$\mathbf {u}''(b;a_{1},a_{2},a_{3})$
for
![]() $b=0$
.) It is easy to see that
$b=0$
.) It is easy to see that
![]() $H_{1,0}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=H_{1,4}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=H_{1,6}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=G(b_{1,2}, b_{1,2}-b_{2,2})\supseteq G_{1,1}(\mathbf {p})$
,
$H_{1,0}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=H_{1,4}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=H_{1,6}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=G(b_{1,2}, b_{1,2}-b_{2,2})\supseteq G_{1,1}(\mathbf {p})$
,
![]() $H_{1,2}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=G(b_{1,2})= G_{1,1}(\mathbf {p})$
, and
$H_{1,2}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=G(b_{1,2})= G_{1,1}(\mathbf {p})$
, and
![]() $H_{1,3}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=H_{1,5} (\partial _{4}\partial _{2}\partial _{2}\mathbf {p}) =H_{1,7}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=G(b_{1,2}-b_{2,2})= G_{1,2}(\mathbf {p})$
. So, Proposition 5.12 holds for
$H_{1,3}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=H_{1,5} (\partial _{4}\partial _{2}\partial _{2}\mathbf {p}) =H_{1,7}(\partial _{4}\partial _{2}\partial _{2}\mathbf {p})=G(b_{1,2}-b_{2,2})= G_{1,2}(\mathbf {p})$
. So, Proposition 5.12 holds for
![]() $\partial _{4}\partial _{2}\partial _{2}\mathbf {p}$
.
$\partial _{4}\partial _{2}\partial _{2}\mathbf {p}$
.
To briefly explain why Proposition 5.12 holds for Example 5.13, we explain, for convenience, why
![]() $H_{1,0}(\mathbf {q})$
contains either
$H_{1,0}(\mathbf {q})$
contains either
![]() $G_{1,0}(\mathbf {p})$
or
$G_{1,0}(\mathbf {p})$
or
![]() $G_{1,2}(\mathbf {p})$
for
$G_{1,2}(\mathbf {p})$
for
![]() $\mathbf {q}=\partial _{2}\mathbf {p},\partial _{2}\partial _{2}\mathbf {p},$
and
$\mathbf {q}=\partial _{2}\mathbf {p},\partial _{2}\partial _{2}\mathbf {p},$
and
![]() $\partial _{4}\partial _{2}\partial _{2}\mathbf {p}$
. Let
$\partial _{4}\partial _{2}\partial _{2}\mathbf {p}$
. Let
![]() $\mathbf {u}(b;a_{1}, \ldots ,a_{s})$
be level data of type
$\mathbf {u}(b;a_{1}, \ldots ,a_{s})$
be level data of type
![]() $(r,i,v)$
and symbol
$(r,i,v)$
and symbol
![]() $\textsf {w}$
, and
$\textsf {w}$
, and
![]() $\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
be level data of type
$\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
be level data of type
![]() $(r',i',v')$
and symbol
$(r',i',v')$
and symbol
![]() $\textsf {w}'$
. We say that the level data
$\textsf {w}'$
. We say that the level data
![]() $\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
dominates (or strictly dominates)
$\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
dominates (or strictly dominates)
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
if
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
if
![]() $i=i'$
,
$i=i'$
,
![]() $\textsf {w}=\textsf {w}'$
and
$\textsf {w}=\textsf {w}'$
and
![]() $\vert v'\vert \geq \vert v\vert $
(or
$\vert v'\vert \geq \vert v\vert $
(or
![]() $\vert v'\vert>\vert v\vert $
, respectively). In Example 5.13, it is not hard to see that for all
$\vert v'\vert>\vert v\vert $
, respectively). In Example 5.13, it is not hard to see that for all
![]() $b\in {\mathbb N}, a_{1}, {a_{2}\in {\mathbb N}_0}$
, if
$b\in {\mathbb N}, a_{1}, {a_{2}\in {\mathbb N}_0}$
, if
![]() $\mathbf {u}'(b;a_{1},a_{2})$
is not of type
$\mathbf {u}'(b;a_{1},a_{2})$
is not of type
![]() $(\ast ,\ast ,2)$
, then there exist
$(\ast ,\ast ,2)$
, then there exist
![]() $b'\in {\mathbb N}, a^{\prime}_{1},a^{\prime}_{2}\in {\mathbb N}_0$
such that
$b'\in {\mathbb N}, a^{\prime}_{1},a^{\prime}_{2}\in {\mathbb N}_0$
such that
![]() $\mathbf {u}'(b';a^{\prime}_{1},a^{\prime}_{2})$
strictly dominates
$\mathbf {u}'(b';a^{\prime}_{1},a^{\prime}_{2})$
strictly dominates
![]() $\mathbf {u}'(b;a_{1},a_{2})$
(in this example,
$\mathbf {u}'(b;a_{1},a_{2})$
(in this example,
![]() $\mathbf {u}'(1;0,0)$
is strictly dominated by
$\mathbf {u}'(1;0,0)$
is strictly dominated by
![]() $\mathbf {u}'(2;0,0)$
). Similar conclusions hold for
$\mathbf {u}'(2;0,0)$
). Similar conclusions hold for
![]() $\mathbf {u}(b;a)$
and
$\mathbf {u}(b;a)$
and
![]() $\mathbf {u}''(b;a_{1},a_{2},a_{3})$
. In other words, the group
$\mathbf {u}''(b;a_{1},a_{2},a_{3})$
. In other words, the group
![]() $H_{1,0}(\mathbf {q})$
must contain the elements of level data of type
$H_{1,0}(\mathbf {q})$
must contain the elements of level data of type
![]() $(\ast ,\ast ,2)$
, and thus it must contain one of
$(\ast ,\ast ,2)$
, and thus it must contain one of
![]() $G_{1,0}(\mathbf {p})$
and
$G_{1,0}(\mathbf {p})$
and
![]() $G_{1,2}(\mathbf {p})$
.
$G_{1,2}(\mathbf {p})$
.
We are now ready to prove Proposition 5.12. The main point is that given any non-trivial level data
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
, we can find another one,
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
, we can find another one,
![]() $\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s}),$
which dominates
$\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s}),$
which dominates
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
and is of type
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
and is of type
![]() $(\ast ,\ast ,v)$
with
$(\ast ,\ast ,v)$
with
![]() $\vert v\vert $
being as large as possible (in this step, we need to exploit the properties (P1)–(P4)). After that, we use the information of the ‘top’ level data
$\vert v\vert $
being as large as possible (in this step, we need to exploit the properties (P1)–(P4)). After that, we use the information of the ‘top’ level data
![]() $\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
to conclude.
$\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
to conclude.
Proof of Proposition 5.12
We start with a claim. Recall that S denotes the set of all
![]() $(a,a')\in {\mathbb N}_0^{2L}$
such that a and
$(a,a')\in {\mathbb N}_0^{2L}$
such that a and
![]() $a'$
are both
$a'$
are both
![]() $\mathbf {0}$
or both different than
$\mathbf {0}$
or both different than
![]() $\mathbf {0}$
(check Definition 2.1 for notation).
$\mathbf {0}$
(check Definition 2.1 for notation).
Claim. Let
![]() $d,s\in {\mathbb N}$
and
$d,s\in {\mathbb N}$
and
![]() $b,a_{1},\ldots ,a_{s},v\in {\mathbb N}_0^{L}$
. If
$b,a_{1},\ldots ,a_{s},v\in {\mathbb N}_0^{L}$
. If
![]() $\vert v\vert \geq \vert b+a_{1}+\cdots +a_{s}\vert $
, then there exist
$\vert v\vert \geq \vert b+a_{1}+\cdots +a_{s}\vert $
, then there exist
![]() $b',a^{\prime}_{1},\ldots ,a^{\prime}_{s}\in {\mathbb N}_0^{L}$
such that
$b',a^{\prime}_{1},\ldots ,a^{\prime}_{s}\in {\mathbb N}_0^{L}$
such that
![]() $(a_{1},a^{\prime}_{1}),\ldots ,(a_{s},a^{\prime}_{s})\in S, \vert b'\vert \geq \vert b\vert $
and
$(a_{1},a^{\prime}_{1}),\ldots ,(a_{s},a^{\prime}_{s})\in S, \vert b'\vert \geq \vert b\vert $
and
![]() $b'+a^{\prime}_{1}+\cdots +a^{\prime}_{s}=v$
.
$b'+a^{\prime}_{1}+\cdots +a^{\prime}_{s}=v$
.
Proof of the claim
To show the claim, we may first assume that
![]() $\vert v\vert =\vert b+a_{1}+\cdots +a_{s}\vert .$
Indeed, if
$\vert v\vert =\vert b+a_{1}+\cdots +a_{s}\vert .$
Indeed, if ![]() , then we write
, then we write
![]() $b'=b+(c,0,\ldots ,0)$
. Then,
$b'=b+(c,0,\ldots ,0)$
. Then,
![]() $\vert b'\vert>\vert b\vert $
and
$\vert b'\vert>\vert b\vert $
and
![]() $\vert v\vert =\vert b'+a_{1}+\cdots +a_{s}\vert .$
$\vert v\vert =\vert b'+a_{1}+\cdots +a_{s}\vert .$
It suffices to show that if
![]() $\vert v-(b+a_{1}+\cdots +a_{s})\vert>0$
, then there exist
$\vert v-(b+a_{1}+\cdots +a_{s})\vert>0$
, then there exist
![]() $b',a^{\prime}_{1},\ldots , a^{\prime}_{s}\in {\mathbb N}_0^{L}$
such that
$b',a^{\prime}_{1},\ldots , a^{\prime}_{s}\in {\mathbb N}_0^{L}$
such that
![]() $(a_{1},a^{\prime}_{1}),\ldots ,(a_{s},a^{\prime}_{s})\in S$
,
$(a_{1},a^{\prime}_{1}),\ldots ,(a_{s},a^{\prime}_{s})\in S$
,
![]() $\vert b'\vert =\vert b\vert $
, and
$\vert b'\vert =\vert b\vert $
, and
![]() $\vert v-(b'+a^{\prime}_{1}+\cdots +a^{\prime}_{s})\vert <\vert v-(b+a_{1}+\cdots +a_{s})\vert $
. Since
$\vert v-(b'+a^{\prime}_{1}+\cdots +a^{\prime}_{s})\vert <\vert v-(b+a_{1}+\cdots +a_{s})\vert $
. Since
![]() $\vert v\vert =\vert b+a_{1}+\cdots +a_{s}\vert $
,
$\vert v\vert =\vert b+a_{1}+\cdots +a_{s}\vert $
,
![]() $\vert v-(b+a_{1}+\cdots +a_{s})\vert $
is at least 2, there exist
$\vert v-(b+a_{1}+\cdots +a_{s})\vert $
is at least 2, there exist
![]() $1\leq i,j\leq L, i\neq j$
such that the tth coordinate of
$1\leq i,j\leq L, i\neq j$
such that the tth coordinate of
![]() $v-(b+a_{1}+\cdots +a_{s})$
is at least
$v-(b+a_{1}+\cdots +a_{s})$
is at least
![]() $1$
for
$1$
for
![]() $t=i$
and is at most
$t=i$
and is at most
![]() $-1$
for
$-1$
for
![]() $t=j$
. We may assume without loss of generality that
$t=j$
. We may assume without loss of generality that
![]() $i=1$
and
$i=1$
and
![]() $j=2$
. Then we have that
$j=2$
. Then we have that
![]() $v_{1}\geq 1$
, and one of
$v_{1}\geq 1$
, and one of
![]() $b_{2},a_{1,2},\ldots ,a_{s,2}$
is at least 1. If
$b_{2},a_{1,2},\ldots ,a_{s,2}$
is at least 1. If
![]() $b_{2}\geq 1$
, then
$b_{2}\geq 1$
, then
![]() $b'=b+(1,-1,0,\ldots ,0)\in {\mathbb N}_0^{L}, a^{\prime}_{i}=a_{i},1\leq i\leq s$
satisfy the requirement. If one of
$b'=b+(1,-1,0,\ldots ,0)\in {\mathbb N}_0^{L}, a^{\prime}_{i}=a_{i},1\leq i\leq s$
satisfy the requirement. If one of
![]() $a_{i,2}$
is positive, then
$a_{i,2}$
is positive, then
![]() $b'=b, a^{\prime}_{i}=a_{i}+(1,-1,0,\ldots ,0)\in {\mathbb N}_0^{L}, a^{\prime}_{j}=a_{j},1\leq j\leq s, j\neq i$
satisfy the requirement. This proves the claim.
$b'=b, a^{\prime}_{i}=a_{i}+(1,-1,0,\ldots ,0)\in {\mathbb N}_0^{L}, a^{\prime}_{j}=a_{j},1\leq j\leq s, j\neq i$
satisfy the requirement. This proves the claim.
Consider the group
![]() $H_{1,m}(\mathbf {q})$
for some
$H_{1,m}(\mathbf {q})$
for some
![]() $0\leq m\leq \ell , m\neq 1$
. Since
$0\leq m\leq \ell , m\neq 1$
. Since
![]() $\mathbf {q}$
is non-degenerate, there exist some
$\mathbf {q}$
is non-degenerate, there exist some
![]() $b,a_{1},\ldots ,a_{s}\in {\mathbb N}_0^{L}, \vert b\vert \geq 1$
such that
$b,a_{1},\ldots ,a_{s}\in {\mathbb N}_0^{L}, \vert b\vert \geq 1$
such that
![]() $u_{1}(b;a_{1},\ldots ,a_{s})-u_{m} (b;a_{1},\ldots , a_{s})\neq \mathbf {0}$
. By property (P1), we may assume that
$u_{1}(b;a_{1},\ldots ,a_{s})-u_{m} (b;a_{1},\ldots , a_{s})\neq \mathbf {0}$
. By property (P1), we may assume that
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is of type
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
is of type
![]() $(r,i,v)$
and has symbol
$(r,i,v)$
and has symbol
![]() $(w_{1},\ldots ,w_{\ell })$
. Since
$(w_{1},\ldots ,w_{\ell })$
. Since
![]() $w_{1}=1$
,
$w_{1}=1$
,
Recall that for
![]() $\mathbf {p}=(p_{1},\ldots ,p_{k})$
,
$\mathbf {p}=(p_{1},\ldots ,p_{k})$
,
![]() $d_{1,0}=\deg (p_{1})$
and
$d_{1,0}=\deg (p_{1})$
and
![]() $d_{1,j}=\deg (p_{1}-p_{j})$
for
$d_{1,j}=\deg (p_{1}-p_{j})$
for
![]() $2\leq j\leq \ell $
. Since
$2\leq j\leq \ell $
. Since
![]() $u_{1}(b;a_{1},\ldots ,a_{s})-u_{m}(b;a_{1},\ldots ,a_{s})\neq \mathbf {0}$
, we have that
$u_{1}(b;a_{1},\ldots ,a_{s})-u_{m}(b;a_{1},\ldots ,a_{s})\neq \mathbf {0}$
, we have that
![]() $w_{m}\neq 1$
and
$w_{m}\neq 1$
and
![]() $\vert v\vert =\vert b+a_{1}+\cdots +a_{s}\vert \leq d_{1,w_{m}}$
.
$\vert v\vert =\vert b+a_{1}+\cdots +a_{s}\vert \leq d_{1,w_{m}}$
.
By the claim, for all
![]() $v'\in {\mathbb N}_0^{L}$
with
$v'\in {\mathbb N}_0^{L}$
with
![]() $\vert v'\vert =d_{1,w_{m}}$
, there exist
$\vert v'\vert =d_{1,w_{m}}$
, there exist
![]() $b',a^{\prime}_{1},\ldots ,a^{\prime}_{s}\in {\mathbb N}_0^{L}$
such that
$b',a^{\prime}_{1},\ldots ,a^{\prime}_{s}\in {\mathbb N}_0^{L}$
such that
![]() $(a_{1},a^{\prime}_{1}),\ldots ,(a_{s},a^{\prime}_{s})\in S$
,
$(a_{1},a^{\prime}_{1}),\ldots ,(a_{s},a^{\prime}_{s})\in S$
,
![]() $\vert b'\vert \geq 1$
and
$\vert b'\vert \geq 1$
and
![]() $b'+a^{\prime}_{1}+\cdots +a^{\prime}_{s}=v'$
. By properties (P2) and (P3),
$b'+a^{\prime}_{1}+\cdots +a^{\prime}_{s}=v'$
. By properties (P2) and (P3),
![]() $\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
is of type
$\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
is of type
![]() $(r',i,v'), r'\neq 0$
and has symbol
$(r',i,v'), r'\neq 0$
and has symbol
![]() $(w_{1},\ldots ,w_{\ell })$
(that is,
$(w_{1},\ldots ,w_{\ell })$
(that is,
![]() $\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
dominates
$\mathbf {u}(b';a^{\prime}_{1},\ldots ,a^{\prime}_{s})$
dominates
![]() $\mathbf {u}(b;a_{1},\ldots ,a_{s})$
). So
$\mathbf {u}(b;a_{1},\ldots ,a_{s})$
). So
In other words, for all
![]() $v'\in {\mathbb N}^{L}$
with
$v'\in {\mathbb N}^{L}$
with
![]() $\vert v'\vert =d_{1,w_{m}}$
, the group
$\vert v'\vert =d_{1,w_{m}}$
, the group
![]() $H_{1,m}(\mathbf {q})$
contains a non-zero multiple of
$H_{1,m}(\mathbf {q})$
contains a non-zero multiple of
![]() $b_{1,v'}-b_{w_{m},v'}$
. So this group contains
$b_{1,v'}-b_{w_{m},v'}$
. So this group contains
![]() $G_{1,w_{m}}(\mathbf {p})$
and we are done.
$G_{1,w_{m}}(\mathbf {p})$
and we are done.
We are now ready to prove Proposition 5.5.
Proof of Proposition 5.5
Let A denote the PET-tuple
![]() $(L,0,k,(f_{1},\!\ldots \!,f_{k}),(p_{1},\!\ldots \!,p_{k}))$
. Then, for all
$(L,0,k,(f_{1},\!\ldots \!,f_{k}),(p_{1},\!\ldots \!,p_{k}))$
. Then, for all
![]() $\tau>0$
,
$\tau>0$
,
 $$ \begin{align*}S(A,\tau)={\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\Vert\mathbb{E}_{n\in I_{N}}\prod_{m=1}^{k}T_{p_{m}(n)}f_{m}\bigg\Vert^{\tau}_{L^{2}(\mu)}.\end{align*} $$
$$ \begin{align*}S(A,\tau)={\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\Vert\mathbb{E}_{n\in I_{N}}\prod_{m=1}^{k}T_{p_{m}(n)}f_{m}\bigg\Vert^{\tau}_{L^{2}(\mu)}.\end{align*} $$
By assumption, A is non-degenerate. We only prove equation (21) for
![]() $f_{1}$
as the other cases are similar. We first assume that A is 1-standard for
$f_{1}$
as the other cases are similar. We first assume that A is 1-standard for
![]() $f_{1}$
. By Theorem 4.9, there exist
$f_{1}$
. By Theorem 4.9, there exist
![]() $t\in {\mathbb N}_{0},$
depending only on
$t\in {\mathbb N}_{0},$
depending only on
![]() $d,k,K,L,$
and finitely many vdC operations
$d,k,K,L,$
and finitely many vdC operations
![]() $\partial _{\rho _{1}},\ldots ,\partial _{\rho _{t}}, \rho _{1},\ldots ,\rho _{t}\neq 1$
such that for all
$\partial _{\rho _{1}},\ldots ,\partial _{\rho _{t}}, \rho _{1},\ldots ,\rho _{t}\neq 1$
such that for all
![]() $1\leq t'\leq t$
,
$1\leq t'\leq t$
,
![]() $\partial _{\rho _{t'}}\ldots \partial _{\rho _{1}}A$
is non-degenerate and 1-standard for
$\partial _{\rho _{t'}}\ldots \partial _{\rho _{1}}A$
is non-degenerate and 1-standard for
![]() $f_{1}$
, and that
$f_{1}$
, and that
![]() $\partial _{\rho _{t'-1}}\ldots \partial _{\rho _{1}}A\to \partial _{\rho _{t'}}\ldots \partial _{\rho _{1}}A$
is 1-inherited. Moreover,
$\partial _{\rho _{t'-1}}\ldots \partial _{\rho _{1}}A\to \partial _{\rho _{t'}}\ldots \partial _{\rho _{1}}A$
is 1-inherited. Moreover,
![]() $A':=\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A$
is of degree 1. By Proposition 4.8,
$A':=\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A$
is of degree 1. By Proposition 4.8,
![]() $S(A, 2^{t})\leq C\cdot S(A',1)$
for some
$S(A, 2^{t})\leq C\cdot S(A',1)$
for some
![]() $C>0$
that depends only on t. Write
$C>0$
that depends only on t. Write
 $$ \begin{align*} S(A',1) &=\overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\Vert\mathbb{E}_{n\in I_{N}} \times \prod_{m=1}^{\ell}T_{\textbf{d}_{m}(h_{1},\ldots,h_{s})\cdot n+r_{m}(h_{1},\ldots,h_{s})}g_{m}(x;h_{1},\ldots,h_{s})\bigg\Vert_{2}\end{align*} $$
$$ \begin{align*} S(A',1) &=\overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\Vert\mathbb{E}_{n\in I_{N}} \times \prod_{m=1}^{\ell}T_{\textbf{d}_{m}(h_{1},\ldots,h_{s})\cdot n+r_{m}(h_{1},\ldots,h_{s})}g_{m}(x;h_{1},\ldots,h_{s})\bigg\Vert_{2}\end{align*} $$
for some
![]() $s,\ell \in \mathbb {N}$
, functions
$s,\ell \in \mathbb {N}$
, functions
![]() $g_{1},\ldots ,g_{\ell }\colon X\times (\mathbb {Z}^{L})^{s}\to \mathbb {R},$
where
$g_{1},\ldots ,g_{\ell }\colon X\times (\mathbb {Z}^{L})^{s}\to \mathbb {R},$
where
![]() $g_{1}(\cdot ;h_{1},\ldots ,h_{s})=f_1$
for all
$g_{1}(\cdot ;h_{1},\ldots ,h_{s})=f_1$
for all
![]() $h_1,\ldots ,h_s$
and such that each
$h_1,\ldots ,h_s$
and such that each
![]() $g_{m}(\cdot ;h_{1},\ldots ,h_{s})$
is an
$g_{m}(\cdot ;h_{1},\ldots ,h_{s})$
is an
![]() $L^{\infty }(\mu )$
function bounded by
$L^{\infty }(\mu )$
function bounded by
![]() $1,$
and polynomials
$1,$
and polynomials
![]() $\textbf {d}_{m}\colon (\mathbb {Z}^{L})^{s}\to (\mathbb {Z}^{d})^{L}$
and
$\textbf {d}_{m}\colon (\mathbb {Z}^{L})^{s}\to (\mathbb {Z}^{d})^{L}$
and
![]() $r_{m}\colon (\mathbb {Z}^{L})^{s}\to \mathbb {Z}^{d}, 1\leq m\leq \ell $
, where the values of
$r_{m}\colon (\mathbb {Z}^{L})^{s}\to \mathbb {Z}^{d}, 1\leq m\leq \ell $
, where the values of
![]() $\textbf {d}_{m}, r_{m}$
are vectors with integer coordinates as vdC operations transform integer-valued polynomials to integer-valued polynomials. (Here,
$\textbf {d}_{m}, r_{m}$
are vectors with integer coordinates as vdC operations transform integer-valued polynomials to integer-valued polynomials. (Here,
![]() $\textbf {d}_{m}(h_{1},\ldots ,h_{s})\cdot n:=n_{1}d_{m,1}(h_{1},\ldots ,h_{s})+\cdots +n_{L}d_{m,L}(h_{1},\ldots ,h_{s})$
, where
$\textbf {d}_{m}(h_{1},\ldots ,h_{s})\cdot n:=n_{1}d_{m,1}(h_{1},\ldots ,h_{s})+\cdots +n_{L}d_{m,L}(h_{1},\ldots ,h_{s})$
, where
![]() $n=(n_{1},\ldots ,n_{L}), n_{i}\in \mathbb {Z},$
and
$n=(n_{1},\ldots ,n_{L}), n_{i}\in \mathbb {Z},$
and
![]() $\textbf {d}_{m}=(d_{m,1},\ldots ,d_{m,L}), d_{m,i}\colon (\mathbb {Z}^{L})^{s}\to \mathbb {Z}^{d}$
.)
$\textbf {d}_{m}=(d_{m,1},\ldots ,d_{m,L}), d_{m,i}\colon (\mathbb {Z}^{L})^{s}\to \mathbb {Z}^{d}$
.)
Let
![]() ${\mathbf {c}}_{1}=-\textbf {d}_{1}$
and
${\mathbf {c}}_{1}=-\textbf {d}_{1}$
and
![]() ${\mathbf {c}}_{m}=\textbf {d}_{m}-\textbf {d}_{1}$
for
${\mathbf {c}}_{m}=\textbf {d}_{m}-\textbf {d}_{1}$
for
![]() $m\neq 1$
. Since
$m\neq 1$
. Since
![]() $A'$
is non-degenerate, we have that
$A'$
is non-degenerate, we have that
![]() ${\mathbf {c}}_{1},\ldots ,{\mathbf {c}}_{s}\not \equiv \mathbf {0}$
. Similar to the proof of [Reference Donoso, Koutsogiannis and Sun7, Proposition 6.1] (see also [Reference Host17, Proposition 1]), if
${\mathbf {c}}_{1},\ldots ,{\mathbf {c}}_{s}\not \equiv \mathbf {0}$
. Similar to the proof of [Reference Donoso, Koutsogiannis and Sun7, Proposition 6.1] (see also [Reference Host17, Proposition 1]), if
![]() $\ell \geq 2$
, we also have that
$\ell \geq 2$
, we also have that
 $$ \begin{align*} S(A',1) & \leq C'\cdot \overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert T_{r_{1}(h_{1},\ldots,h_{s})}f_1\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{\{G'({\mathbf{c}}_{i}(h_{1},\ldots,h_{s}))\}_{1\leq i\leq \ell}} \\ & = C'\cdot\overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_{1}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{\{G'({\mathbf{c}}_{i}(h_{1},\ldots,h_{s}))\}_{1\leq i\leq \ell}} \end{align*} $$
$$ \begin{align*} S(A',1) & \leq C'\cdot \overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert T_{r_{1}(h_{1},\ldots,h_{s})}f_1\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{\{G'({\mathbf{c}}_{i}(h_{1},\ldots,h_{s}))\}_{1\leq i\leq \ell}} \\ & = C'\cdot\overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}}\lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_{1}\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{\{G'({\mathbf{c}}_{i}(h_{1},\ldots,h_{s}))\}_{1\leq i\leq \ell}} \end{align*} $$
for some
![]() $C'>0$
depending only on
$C'>0$
depending only on
![]() $\ell $
. If
$\ell $
. If
![]() $\ell =1$
, using the mean ergodic theorem (see for example [Reference Donoso, Koutsogiannis and Sun7, Theorem 2.3]) and [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.4(iv), (vi)], we have
$\ell =1$
, using the mean ergodic theorem (see for example [Reference Donoso, Koutsogiannis and Sun7, Theorem 2.3]) and [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.4(iv), (vi)], we have
 $$ \begin{align*} S(A',1) & = \overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}} \Vert \mathbb{E}(T_{r_{1}(h_{1},\ldots,h_{s})}f_1\vert \mathcal{I}({\mathbf{c}}_{1}(h_{1},\ldots,h_{s})))\Vert_{2} \\ & = \overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}} \Vert \mathbb{E}(f_1\vert \mathcal{I}({\mathbf{c}}_{1}(h_{1},\ldots,h_{s})))\Vert_{2} \\ & = \overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_1\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{G'({\mathbf{c}}_{1}(h_{1},\ldots,h_{s}))}. \end{align*} $$
$$ \begin{align*} S(A',1) & = \overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}} \Vert \mathbb{E}(T_{r_{1}(h_{1},\ldots,h_{s})}f_1\vert \mathcal{I}({\mathbf{c}}_{1}(h_{1},\ldots,h_{s})))\Vert_{2} \\ & = \overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}} \Vert \mathbb{E}(f_1\vert \mathcal{I}({\mathbf{c}}_{1}(h_{1},\ldots,h_{s})))\Vert_{2} \\ & = \overline{\mathbb{E}}^{\square}_{h_{1},\ldots,h_{s}\in\mathbb{Z}^{L}} \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_1\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{G'({\mathbf{c}}_{1}(h_{1},\ldots,h_{s}))}. \end{align*} $$
Combining this with the fact that
![]() $S(A,2^{t})\leq C\cdot S(A',1)$
, we get equation (21).
$S(A,2^{t})\leq C\cdot S(A',1)$
, we get equation (21).
We now consider the groups
![]() $H_{1,m}, 0\leq m\leq \ell , m\neq 1$
. Suppose that
$H_{1,m}, 0\leq m\leq \ell , m\neq 1$
. Suppose that
 $$ \begin{align*}\textbf{c}_{m}(h_{1},\ldots,h_{s})=\sum_{a_{1},\ldots,a_{s}\in\mathbb{N}_0^L}h^{a_{1}}_{1}\ldots h^{a_{s}}_{s}\cdot {\mathbf{v}}_{m}(a_{1},\ldots,a_{s})\end{align*} $$
$$ \begin{align*}\textbf{c}_{m}(h_{1},\ldots,h_{s})=\sum_{a_{1},\ldots,a_{s}\in\mathbb{N}_0^L}h^{a_{1}}_{1}\ldots h^{a_{s}}_{s}\cdot {\mathbf{v}}_{m}(a_{1},\ldots,a_{s})\end{align*} $$
and
 $$ \begin{align*} \textbf{d}_{m}(h_{1},\ldots,h_{s})=\sum_{a_{1},\ldots,a_{s}\in\mathbb{N}_0^L}h^{a_{1}}_{1}\ldots h^{a_{s}}_{s}\cdot \mathbf{u}_{m}(a_{1},\ldots,a_{s})\end{align*} $$
$$ \begin{align*} \textbf{d}_{m}(h_{1},\ldots,h_{s})=\sum_{a_{1},\ldots,a_{s}\in\mathbb{N}_0^L}h^{a_{1}}_{1}\ldots h^{a_{s}}_{s}\cdot \mathbf{u}_{m}(a_{1},\ldots,a_{s})\end{align*} $$
for some vectors
![]() $\mathbf {u}_{m}(a_{1},\ldots ,a_{s})=(u_{m,1}(a_{1},\ldots ,a_{s}),\ldots ,u_{m,L}(a_{1},\ldots ,a_{s}))$
, and
$\mathbf {u}_{m}(a_{1},\ldots ,a_{s})=(u_{m,1}(a_{1},\ldots ,a_{s}),\ldots ,u_{m,L}(a_{1},\ldots ,a_{s}))$
, and
![]() ${\mathbf {v}}_{m}(a_{1},\ldots ,a_{s}) =(v_{m,1}(a_{1},\ldots ,a_{s}),\ldots ,v_{m,L}(a_{1},\ldots ,a_{s}))\in (\mathbb {Q}^{d})^{L}$
with all but finitely many terms being zero for each m. Obviously A satisfies properties (P1)–(P4) (recall that the first coordinate of a symbol can always be chosen to be 1 by the comment after Definition 5.7).
${\mathbf {v}}_{m}(a_{1},\ldots ,a_{s}) =(v_{m,1}(a_{1},\ldots ,a_{s}),\ldots ,v_{m,L}(a_{1},\ldots ,a_{s}))\in (\mathbb {Q}^{d})^{L}$
with all but finitely many terms being zero for each m. Obviously A satisfies properties (P1)–(P4) (recall that the first coordinate of a symbol can always be chosen to be 1 by the comment after Definition 5.7).
![]() $A'=\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A$
satisfies, by Proposition 5.11, properties (P1)–(P4). Since
$A'=\partial _{\rho _{t}}\ldots \partial _{\rho _{1}}A$
satisfies, by Proposition 5.11, properties (P1)–(P4). Since
![]() $\deg (A')=1$
, by Proposition 5.12, each of
$\deg (A')=1$
, by Proposition 5.12, each of
 $$ \begin{align*} & G(\{v_{1,j}(a_{1},\ldots,a_{s})\colon (a_{1},\ldots,a_{s})\in({\mathbb N}_0^{L})^{s}, 1\leq j\leq L\}) \\&\quad =G(\{u_{1,j}(a_{1},\ldots,a_{s})\colon (a_{1},\ldots,a_{s})\in({\mathbb N}_0^{L})^{s}, 1\leq j\leq L\})=H_{1,0}, \end{align*} $$
$$ \begin{align*} & G(\{v_{1,j}(a_{1},\ldots,a_{s})\colon (a_{1},\ldots,a_{s})\in({\mathbb N}_0^{L})^{s}, 1\leq j\leq L\}) \\&\quad =G(\{u_{1,j}(a_{1},\ldots,a_{s})\colon (a_{1},\ldots,a_{s})\in({\mathbb N}_0^{L})^{s}, 1\leq j\leq L\})=H_{1,0}, \end{align*} $$
and
 $$ \begin{align*} &G(\{v_{m,j}(a_{1},\ldots,a_{s})\colon (a_{1},\ldots,a_{s})\in({\mathbb N}_0^{L})^{s}\})\\ &\quad =G(\{u_{1,j}(a_{1},\ldots,a_{s})-u_{m,j}(a_{1},\ldots,a_{s})\colon (a_{1},\ldots,a_{s})\in({\mathbb N}_0^{L})^{s}\})\\ &\quad =H_{1,m},\; 2\leq m\leq \ell, \end{align*} $$
$$ \begin{align*} &G(\{v_{m,j}(a_{1},\ldots,a_{s})\colon (a_{1},\ldots,a_{s})\in({\mathbb N}_0^{L})^{s}\})\\ &\quad =G(\{u_{1,j}(a_{1},\ldots,a_{s})-u_{m,j}(a_{1},\ldots,a_{s})\colon (a_{1},\ldots,a_{s})\in({\mathbb N}_0^{L})^{s}\})\\ &\quad =H_{1,m},\; 2\leq m\leq \ell, \end{align*} $$
contains some of the groups
![]() $G_{1,j}(\mathbf {p}), 0\leq j\leq k, j\neq 1$
.
$G_{1,j}(\mathbf {p}), 0\leq j\leq k, j\neq 1$
.
Next we assume that A is not 1-standard for
![]() $f_{1}$
. In this case, we need to invoke a ‘dimension increment’ argument to convert A to be 1-standard for
$f_{1}$
. In this case, we need to invoke a ‘dimension increment’ argument to convert A to be 1-standard for
![]() $f_{1}$
. We may assume without loss of generality that
$f_{1}$
. We may assume without loss of generality that
![]() $p_{k}$
has the highest degree. Since A is semi-standard for
$p_{k}$
has the highest degree. Since A is semi-standard for
![]() $f_{1}$
, by [Reference Donoso, Koutsogiannis and Sun7, Proposition 6.3], there exists a PET-tuple
$f_{1}$
, by [Reference Donoso, Koutsogiannis and Sun7, Proposition 6.3], there exists a PET-tuple
![]() $A'=(2L,0,\ell ,\mathbf {p}',\mathbf {g})$
which is non-degenerate and 1-standard for
$A'=(2L,0,\ell ,\mathbf {p}',\mathbf {g})$
which is non-degenerate and 1-standard for
![]() $f_{1}$
such that
$f_{1}$
such that
![]() $S(A,2\tau )\leq S(A',\tau )$
for all
$S(A,2\tau )\leq S(A',\tau )$
for all
![]() $\tau>0$
. Moreover,
$\tau>0$
. Moreover,
![]() $\mathbf {p}'$
is obtained by selecting some polynomials from the family
$\mathbf {p}'$
is obtained by selecting some polynomials from the family
with
![]() $2L$
-dimensional variables
$2L$
-dimensional variables
![]() $(n,n'),$
where
$(n,n'),$
where
![]() $p_{1}(n)-p_{k}(n')$
is selected in
$p_{1}(n)-p_{k}(n')$
is selected in
![]() $\mathbf {p}'$
and is associated to
$\mathbf {p}'$
and is associated to
![]() $f_{1}$
. It is not hard to check that
$f_{1}$
. It is not hard to check that
![]() $G_{1,j}(\mathbf {q})=G_{1,j}(\mathbf {p})$
for
$G_{1,j}(\mathbf {q})=G_{1,j}(\mathbf {p})$
for
![]() $0\leq j\leq k, j\neq 1$
. Moreover, for
$0\leq j\leq k, j\neq 1$
. Moreover, for
![]() $1\leq j\leq k-1$
,
$1\leq j\leq k-1$
,
![]() $G_{1,k+j}(\mathbf {q})=G_{1,0}(\mathbf {p})+G_{j,0}(\mathbf {p})\supseteq G_{1,0}(\mathbf {p})$
if
$G_{1,k+j}(\mathbf {q})=G_{1,0}(\mathbf {p})+G_{j,0}(\mathbf {p})\supseteq G_{1,0}(\mathbf {p})$
if
![]() $d_{1,0}=d_{j,0}$
,
$d_{1,0}=d_{j,0}$
,
![]() $G_{1,k+j}(\mathbf {q})=G_{1,0}(\mathbf {p})=G_{1,j}(\mathbf {q})$
if
$G_{1,k+j}(\mathbf {q})=G_{1,0}(\mathbf {p})=G_{1,j}(\mathbf {q})$
if
![]() $d_{1,0}>d_{j,0}$
, and
$d_{1,0}>d_{j,0}$
, and
![]() $G_{1,k+j}(\mathbf {q})=G_{j,0}(\mathbf {p})=G_{1,j}(\mathbf {q})$
if
$G_{1,k+j}(\mathbf {q})=G_{j,0}(\mathbf {p})=G_{1,j}(\mathbf {q})$
if
![]() $d_{1,0}<d_{j,0}$
. In other words, each
$d_{1,0}<d_{j,0}$
. In other words, each
![]() $G_{1,j}(\mathbf {q}),$
and thus each
$G_{1,j}(\mathbf {q}),$
and thus each
![]() $G_{1,j}(\mathbf {p}'),$
contains some
$G_{1,j}(\mathbf {p}'),$
contains some
![]() $G_{1,j'}(\mathbf {p}).$
Applying the previous conclusion to
$G_{1,j'}(\mathbf {p}).$
Applying the previous conclusion to
![]() $A'$
, we are done.
$A'$
, we are done.
Finally, the fact that each
![]() ${\mathbf {v}}_{i,m}(a_{1},\ldots ,a_{s})$
is a polynomial function in terms of the coefficients of
${\mathbf {v}}_{i,m}(a_{1},\ldots ,a_{s})$
is a polynomial function in terms of the coefficients of
![]() $p_{i}, 1\leq i\leq k,$
whose degree depends only on
$p_{i}, 1\leq i\leq k,$
whose degree depends only on
![]() $d,k,K,L,$
follows easily from the polynomial nature of the vdC operations.
$d,k,K,L,$
follows easily from the polynomial nature of the vdC operations.
We now have all the ingredients needed to prove Theorem 2.11. In fact, Theorem 2.11 has a proof similar to that of [Reference Donoso, Koutsogiannis and Sun7, Theorem 5.1].
Proof of Theorem 2.11
By Propositions 5.5 and 5.2, and the definition of Host–Kra characteristic factors, the left-hand side of equation (10) is 0 if for some
![]() $1\leq i\leq k$
,
$1\leq i\leq k$
,
![]() $f_{i}$
is orthogonal to
$f_{i}$
is orthogonal to
![]() $Z_{\{H_{i,m}\}_{1\leq m\leq t_{i}}^{\times D_{i}}}(\mathbf {X})$
for some
$Z_{\{H_{i,m}\}_{1\leq m\leq t_{i}}^{\times D_{i}}}(\mathbf {X})$
for some
![]() $t_{i},D_{i}\in {\mathbb N}$
, where
$t_{i},D_{i}\in {\mathbb N}$
, where
![]() $H_{i,m}$
is defined as in Proposition 5.5. By Proposition 5.5,
$H_{i,m}$
is defined as in Proposition 5.5. By Proposition 5.5,
![]() $H_{i,m}$
is contained in one of
$H_{i,m}$
is contained in one of
![]() $G_{i,j}(\mathbf {p}), 0\leq j\leq k, j\neq i$
. Using Proposition 3.1(v), if some
$G_{i,j}(\mathbf {p}), 0\leq j\leq k, j\neq i$
. Using Proposition 3.1(v), if some
![]() $f_{i}, 1\leq i\leq k$
, is orthogonal to
$f_{i}, 1\leq i\leq k$
, is orthogonal to
![]() $Z_{\{G_{i,j}(\mathbf {p})\}_{0\leq j\leq k, j\neq i}^{\times D_{i}t_{i}}}(\mathbf {X})$
, then it is also orthogonal to
$Z_{\{G_{i,j}(\mathbf {p})\}_{0\leq j\leq k, j\neq i}^{\times D_{i}t_{i}}}(\mathbf {X})$
, then it is also orthogonal to
![]() $Z_{\{H_{i,m}\}_{1\leq m\leq t_{i}}^{\times D_{i}}}(\mathbf {X})$
, and thus the left-hand side of equation (10) is 0.
$Z_{\{H_{i,m}\}_{1\leq m\leq t_{i}}^{\times D_{i}}}(\mathbf {X})$
, and thus the left-hand side of equation (10) is 0.
The ‘in particular’ part follows from Corollary 3.2.
Remark 5.14. We remark that the number D derived in Theorem 2.11 is not optimal.
To see this, recall that this number indicates the step of the nilsequence in the splitting results. For multicorrelation sequences with general polynomial iterates, this D can be taken to be equal to the number of vdC operations we have to perform for all the iterates to become constant (e.g. [Reference Frantzikinakis and Host10] via [Reference Frantzikinakis13], and [Reference Koutsogiannis25] via [Reference Frantzikinakis and Host10]). At this point, a word of caution is necessary for the approach of this paper. Specifically, while the number D in Theorem 2.11 can still be chosen to be the number of transformations in the case of linear iterates (given that there is no dependence on h—the variables arising from the vdC operations), in the general case, the picture is quite different. By carefully tracking the constants that appear in Propositions 5.2 and 5.4, D can be chosen to be the maximum of
![]() $t_{i}s_{i}^{[t_{i}(s^{\prime}_{i}+1)^{s_{i}L}]+1}, 1\leq i\leq k$
, where
$t_{i}s_{i}^{[t_{i}(s^{\prime}_{i}+1)^{s_{i}L}]+1}, 1\leq i\leq k$
, where
![]() $s^{\prime}_{i}$
is the degree of
$s^{\prime}_{i}$
is the degree of
![]() $\mathbf {p}$
,
$\mathbf {p}$
,
![]() $t_{i}$
is the number of terms remaining when
$t_{i}$
is the number of terms remaining when
![]() $\mathbf {{p}}$
is converted to a linear family which is 1-standard for
$\mathbf {{p}}$
is converted to a linear family which is 1-standard for
![]() $f_{i}$
for the first time, and
$f_{i}$
for the first time, and
![]() $s_{i}$
is
$s_{i}$
is
![]() $t_{i}$
plus the number of vdC operations needed to convert
$t_{i}$
plus the number of vdC operations needed to convert
![]() $\mathbf {p}$
in such a way. (The details are left to the interested readers.)
$\mathbf {p}$
in such a way. (The details are left to the interested readers.)
6 Proof of main results
Using Theorem 2.11, we prove in this section Theorems 2.2, 2.5, and 2.9.
Proof of Theorem 2.2
We follow and adapt the proof strategy in [Reference Leibman28, §3]. To avoid confusion, we use
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert \cdot \rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert $
to denote the Host–Kra seminorm on the
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert \cdot \rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert $
to denote the Host–Kra seminorm on the
![]() ${\mathbb Z}^{d}$
-system
${\mathbb Z}^{d}$
-system
![]() $(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^{d}}),$
and
$(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^{d}}),$
and
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert \cdot \rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert '$
to denote the Host–Kra seminorm on the
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert \cdot \rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert '$
to denote the Host–Kra seminorm on the
![]() ${\mathbb Z}^{d}$
-system
${\mathbb Z}^{d}$
-system
![]() $(X^{2},\mathcal {B}^{2},\mu ^{\otimes 2}, (S_{n})_{n\in {\mathbb Z}^{d}})$
, where
$(X^{2},\mathcal {B}^{2},\mu ^{\otimes 2}, (S_{n})_{n\in {\mathbb Z}^{d}})$
, where
![]() $S_{n}=T_{n}\times T_{n}$
.
$S_{n}=T_{n}\times T_{n}$
.
Let
![]() $(I_N)_{N\in {\mathbb N}}$
be a Følner sequence in
$(I_N)_{N\in {\mathbb N}}$
be a Følner sequence in
![]() ${\mathbb Z}^L$
. Note that
${\mathbb Z}^L$
. Note that
 $$ \begin{align} & \lim_{N \to \infty} \frac{1}{|I_N|} \sum_{n \in I_N} \bigg| \int_X f_0\cdot T_{p_1(n)}f_1 \cdots T_{p_k(n)} f_k \, d\mu \bigg|^2\nonumber \\&\quad = \lim_{N \to \infty} \frac{1}{|I_N|} \sum_{n \in I_N} \int_{X^2} f_0 \otimes \bar{f_0} \cdot \prod_{i=1}^k S_{p_i(n)} (f_i \otimes \bar{f_i}) \, d(\mu\times \mu). \end{align} $$
$$ \begin{align} & \lim_{N \to \infty} \frac{1}{|I_N|} \sum_{n \in I_N} \bigg| \int_X f_0\cdot T_{p_1(n)}f_1 \cdots T_{p_k(n)} f_k \, d\mu \bigg|^2\nonumber \\&\quad = \lim_{N \to \infty} \frac{1}{|I_N|} \sum_{n \in I_N} \int_{X^2} f_0 \otimes \bar{f_0} \cdot \prod_{i=1}^k S_{p_i(n)} (f_i \otimes \bar{f_i}) \, d(\mu\times \mu). \end{align} $$
By Theorem 2.11, there exists
![]() $D'\in {\mathbb N}$
such that for all
$D'\in {\mathbb N}$
such that for all
![]() $1 \leq i \leq k$
, equation (27) equals to 0 if
$1 \leq i \leq k$
, equation (27) equals to 0 if
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_i \otimes \bar {f_i}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert ^{\prime}_{\{\tilde {G}_{i,j}(\mathbf {p})\}^{\times D'}_{0\leq j\leq k, j\neq i}}=0$
, where
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_i \otimes \bar {f_i}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert ^{\prime}_{\{\tilde {G}_{i,j}(\mathbf {p})\}^{\times D'}_{0\leq j\leq k, j\neq i}}=0$
, where
![]() $\tilde {G}_{i,j}(\mathbf {p})$
is the group action generated by
$\tilde {G}_{i,j}(\mathbf {p})$
is the group action generated by
![]() $S_{n}$
for all
$S_{n}$
for all
![]() $n\in G_{i,j}(\mathbf {p})$
. (Strictly speaking,
$n\in G_{i,j}(\mathbf {p})$
. (Strictly speaking,
![]() $G_{i,j}(\mathbf {p})$
and
$G_{i,j}(\mathbf {p})$
and
![]() $\tilde {G}_{i,j}(\mathbf {p})$
are the same subgroup of
$\tilde {G}_{i,j}(\mathbf {p})$
are the same subgroup of
![]() ${\mathbb Z}^{d}$
. We distinguish these two notions to indicate that
${\mathbb Z}^{d}$
. We distinguish these two notions to indicate that
![]() $G_{i,j}(\mathbf {p})$
and
$G_{i,j}(\mathbf {p})$
and
![]() $\tilde {G}_{i,j}(\mathbf {p})$
are attached to the distinct group actions
$\tilde {G}_{i,j}(\mathbf {p})$
are attached to the distinct group actions
![]() $(T_{n})_{n\in G_{i,j}(\mathbf {p})}$
and
$(T_{n})_{n\in G_{i,j}(\mathbf {p})}$
and
![]() $(S_{n})_{n\in G^{\prime}_{i,j}(\mathbf {p})}$
.) Using Lemma 3.4,
$(S_{n})_{n\in G^{\prime}_{i,j}(\mathbf {p})}$
.) Using Lemma 3.4,
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_i \otimes \bar {f_i}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert ^{\prime}_{\{\tilde {G}_{i,j}(\mathbf {p})\}^{\times D'}_{0\leq j\leq k, j\neq i}}$
is bounded by
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_i \otimes \bar {f_i}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert ^{\prime}_{\{\tilde {G}_{i,j}(\mathbf {p})\}^{\times D'}_{0\leq j\leq k, j\neq i}}$
is bounded by
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_i\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert ^2_{\{G_{i,j}(\mathbf {p})\}^{\times D'}_{0\leq j\leq k, j\neq i},{\mathbb Z}^{d}}$
, which is equal to
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_i\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert ^2_{\{G_{i,j}(\mathbf {p})\}^{\times D'}_{0\leq j\leq k, j\neq i},{\mathbb Z}^{d}}$
, which is equal to
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_i\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert ^2_{({\mathbb Z}^{d})^{\times (D+1)}}$
with
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_i\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert ^2_{({\mathbb Z}^{d})^{\times (D+1)}}$
with
![]() $D=kD'$
by our ergodicity assumptions and Corollary 3.2.
$D=kD'$
by our ergodicity assumptions and Corollary 3.2.
Therefore, for
![]() $1 \leq i\leq k$
, we have
$1 \leq i\leq k$
, we have
 $$ \begin{align} \lim_{N \to \infty} \frac{1}{|I_N|} \sum_{n \in I_N} \int_{X^2} (f_0 \otimes \bar{f_0}) \cdot \prod_{i=1}^k S_{p_i(n)} (f_i \otimes \bar{f_i}) \, d(\mu \times\mu)=0 \text{ if } \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_i\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{({\mathbb Z}^d)^{\times (D+1)}}=0. \end{align} $$
$$ \begin{align} \lim_{N \to \infty} \frac{1}{|I_N|} \sum_{n \in I_N} \int_{X^2} (f_0 \otimes \bar{f_0}) \cdot \prod_{i=1}^k S_{p_i(n)} (f_i \otimes \bar{f_i}) \, d(\mu \times\mu)=0 \text{ if } \lvert\hspace{-1pt}\lvert\hspace{-1pt}\lvert f_i\rvert\hspace{-1pt}\rvert\hspace{-1pt}\rvert_{({\mathbb Z}^d)^{\times (D+1)}}=0. \end{align} $$
Then, equation (28) and Theorem 3.5 imply that the sequence
is a nullsequence.
Let
![]() $\varepsilon>0$
. By our assumption,
$\varepsilon>0$
. By our assumption,
![]() $\mathbf {X}$
is ergodic. The factor
$\mathbf {X}$
is ergodic. The factor
![]() $Z_{({\mathbb Z}^{d})^{\times (D+1)}}(\mathbf {X}),$
via Theorem 3.5, is an inverse limit of D-step nilsystems. Thus, there exists a factor of
$Z_{({\mathbb Z}^{d})^{\times (D+1)}}(\mathbf {X}),$
via Theorem 3.5, is an inverse limit of D-step nilsystems. Thus, there exists a factor of
![]() $Z_{({\mathbb Z}^{d})^{\times (D+1)}}(\mathbf {X})$
with the structure of a D-step nilsystem
$Z_{({\mathbb Z}^{d})^{\times (D+1)}}(\mathbf {X})$
with the structure of a D-step nilsystem
![]() $(\tilde {X},\mathcal {B}(\tilde {X}),\mu _{\tilde {X}}, T_1,\ldots ,T_d)$
, on which each
$(\tilde {X},\mathcal {B}(\tilde {X}),\mu _{\tilde {X}}, T_1,\ldots ,T_d)$
, on which each
![]() $T_i$
acts as a niltranslation by an element
$T_i$
acts as a niltranslation by an element
![]() $a_i \in \tilde {X}$
, such that for
$a_i \in \tilde {X}$
, such that for
![]() $\tilde {f_i}=\mathbb {E}(f_i \mid \tilde {X})$
and
$\tilde {f_i}=\mathbb {E}(f_i \mid \tilde {X})$
and ![]() we have
we have
 $$ \begin{align*} \bigg|\int_{X} f_0 \cdot \prod_{i=1}^k T_{p_i(n)} \mathbb{E}(f_i \mid Z_{({\mathbb Z}^{d})^{\times (D+1)}}(\mathbf{X})) \, d\mu-\int_{\tilde{X}} \tilde{f_0} \cdot \prod_{i=1}^k \vec{a}_{p_i(n)}\tilde{f_i} \ d\mu_{\tilde{X}} \bigg|<\varepsilon\end{align*} $$
$$ \begin{align*} \bigg|\int_{X} f_0 \cdot \prod_{i=1}^k T_{p_i(n)} \mathbb{E}(f_i \mid Z_{({\mathbb Z}^{d})^{\times (D+1)}}(\mathbf{X})) \, d\mu-\int_{\tilde{X}} \tilde{f_0} \cdot \prod_{i=1}^k \vec{a}_{p_i(n)}\tilde{f_i} \ d\mu_{\tilde{X}} \bigg|<\varepsilon\end{align*} $$
for all
![]() $n \in {\mathbb Z}^L$
, where, if
$n \in {\mathbb Z}^L$
, where, if
![]() $p_{i}=(p_{i,1},\ldots ,p_{i,d}),$
then
$p_{i}=(p_{i,1},\ldots ,p_{i,d}),$
then
![]() $\vec {a}_{p_i(n)}$
denotes the niltranslation by the element
$\vec {a}_{p_i(n)}$
denotes the niltranslation by the element
![]() $(a_1^{p_{i,1}(n)},\ldots ,a_d^{p_{i,d}(n)})$
. Therefore, there exists a nullsequence
$(a_1^{p_{i,1}(n)},\ldots ,a_d^{p_{i,d}(n)})$
. Therefore, there exists a nullsequence
![]() $\Lambda $
such that
$\Lambda $
such that
 $$ \begin{align} \bigg\Vert a(n)-\bigg(\int_{\tilde{X}} \tilde{f_0} \cdot \vec{a}_{p_1(n)}\tilde{f_1} \cdots \vec{a}_{p_k(n)} \tilde{f_k} \, d\mu_{\tilde{X}}+\Lambda(n)\bigg)\bigg\Vert_{\ell^{\infty}({\mathbb Z}^L)}<\varepsilon. \end{align} $$
$$ \begin{align} \bigg\Vert a(n)-\bigg(\int_{\tilde{X}} \tilde{f_0} \cdot \vec{a}_{p_1(n)}\tilde{f_1} \cdots \vec{a}_{p_k(n)} \tilde{f_k} \, d\mu_{\tilde{X}}+\Lambda(n)\bigg)\bigg\Vert_{\ell^{\infty}({\mathbb Z}^L)}<\varepsilon. \end{align} $$
A standard approximation argument allows us to assume without loss of generality that
![]() $\tilde {f_1},\ldots ,\tilde {f_k} \in C(\tilde {X})$
in equation (30). Applying [Reference Leibman28, Theorem 2.5] to the nilmanifold
$\tilde {f_1},\ldots ,\tilde {f_k} \in C(\tilde {X})$
in equation (30). Applying [Reference Leibman28, Theorem 2.5] to the nilmanifold
![]() $\tilde {X}^k$
, the diagonal subnilmanifold
$\tilde {X}^k$
, the diagonal subnilmanifold
![]() $\{(x,\ldots ,x) : x \in \tilde {X}\}$
, the polynomial sequence
$\{(x,\ldots ,x) : x \in \tilde {X}\}$
, the polynomial sequence
![]() $(\vec {a}_{p_1(n)},\ldots ,\vec {a}_{p_k(n)}),$
and the function
$(\vec {a}_{p_1(n)},\ldots ,\vec {a}_{p_k(n)}),$
and the function
![]() $f(x_1,\ldots ,x_k)=\tilde {f_1}(x_1)\cdots \tilde {f_k}(x_k) \in C(\tilde {X}^k)$
, we obtain that the sequence
$f(x_1,\ldots ,x_k)=\tilde {f_1}(x_1)\cdots \tilde {f_k}(x_k) \in C(\tilde {X}^k)$
, we obtain that the sequence
is a sum of a D-step nilsequence and a nullsequence.
Therefore, for each
![]() $\varepsilon>0$
, we can find a D-step nilsequence
$\varepsilon>0$
, we can find a D-step nilsequence
![]() $\psi $
(the one described above), a nullsequence
$\psi $
(the one described above), a nullsequence
![]() $\Lambda ,$
and a bounded sequence
$\Lambda ,$
and a bounded sequence
![]() $\delta $
with
$\delta $
with
![]() $\Vert \delta \Vert _{\ell ^{\infty }({\mathbb Z}^L)} \leq \varepsilon ,$
such that
$\Vert \delta \Vert _{\ell ^{\infty }({\mathbb Z}^L)} \leq \varepsilon ,$
such that
For each
![]() $l \in {\mathbb N}$
, consider the decomposition
$l \in {\mathbb N}$
, consider the decomposition
![]() $a=\psi _l+\Lambda _l+\delta _l$
, where
$a=\psi _l+\Lambda _l+\delta _l$
, where
![]() $\Vert \delta _l\Vert _{\ell ^{\infty }({\mathbb Z}^L)}<{1}/{l}$
. For
$\Vert \delta _l\Vert _{\ell ^{\infty }({\mathbb Z}^L)}<{1}/{l}$
. For
![]() $r \neq l$
, we have
$r \neq l$
, we have
Now,
![]() $\lim _{|I_N| \to \infty } {1}/{|I_N|}\sum _{n \in I_N} \vert \Lambda _l(n)-\Lambda _r(n)\vert =0$
and
$\lim _{|I_N| \to \infty } {1}/{|I_N|}\sum _{n \in I_N} \vert \Lambda _l(n)-\Lambda _r(n)\vert =0$
and
![]() $\sup _{n \in {\mathbb Z}^L} \vert \delta _r(n)-\delta _l(n)\vert \leq {1}/{l} + {1}/{r}$
. Therefore,
$\sup _{n \in {\mathbb Z}^L} \vert \delta _r(n)-\delta _l(n)\vert \leq {1}/{l} + {1}/{r}$
. Therefore,
for all
![]() $n \in {\mathbb Z}^L$
except potentially a subset
$n \in {\mathbb Z}^L$
except potentially a subset
![]() $A \subseteq {\mathbb Z}^L,$
with its characteristic function,
$A \subseteq {\mathbb Z}^L,$
with its characteristic function, ![]() being a nullsequence. For each
being a nullsequence. For each
![]() $l, r \in {\mathbb N}$
, the sequence
$l, r \in {\mathbb N}$
, the sequence
![]() $\psi _l(n)-\psi _r(n)$
is a nilsequence, so, by the same argument in the proof of [Reference Leibman28, Theorem 3.1], it follows that the inequality in equation (33) must, in fact, hold for all
$\psi _l(n)-\psi _r(n)$
is a nilsequence, so, by the same argument in the proof of [Reference Leibman28, Theorem 3.1], it follows that the inequality in equation (33) must, in fact, hold for all
![]() $n \in {\mathbb Z}^L$
. Hence, the sequence
$n \in {\mathbb Z}^L$
. Hence, the sequence
![]() $(\psi _l)_{l \in {\mathbb N}}$
is a Cauchy sequence in
$(\psi _l)_{l \in {\mathbb N}}$
is a Cauchy sequence in
![]() $\ell ^{\infty }({\mathbb Z}^L)$
that consists of D-step nilsequences, and since we already showed that
$\ell ^{\infty }({\mathbb Z}^L)$
that consists of D-step nilsequences, and since we already showed that
![]() $(\delta _r)_{r \in {\mathbb N}}$
is a Cauchy sequence in
$(\delta _r)_{r \in {\mathbb N}}$
is a Cauchy sequence in
![]() $\ell ^{\infty }({\mathbb Z}^L)$
converging to a nullsequence, the conclusion follows.
$\ell ^{\infty }({\mathbb Z}^L)$
converging to a nullsequence, the conclusion follows.
Remark 6.1. It is worth noting that if the polynomials
![]() $p_{1},\ldots ,p_{k}$
are linear, then there is an easier proof of Theorem 2.2, where one has
$p_{1},\ldots ,p_{k}$
are linear, then there is an easier proof of Theorem 2.2, where one has
![]() $D=k$
. The reason is that, instead of Theorem 2.11, one can use [Reference Host17, Proposition 1] or [Reference Donoso, Koutsogiannis and Sun7, Proposition 6.1] to improve the right-hand side of equation (28) to
$D=k$
. The reason is that, instead of Theorem 2.11, one can use [Reference Host17, Proposition 1] or [Reference Donoso, Koutsogiannis and Sun7, Proposition 6.1] to improve the right-hand side of equation (28) to
![]() $\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_{i}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert ^{2}_{({\mathbb Z}^{d})^{\times (k+1)}}$
.
$\lvert \hspace{-1pt}\lvert \hspace{-1pt}\lvert f_{i}\rvert \hspace{-1pt}\rvert \hspace{-1pt}\rvert ^{2}_{({\mathbb Z}^{d})^{\times (k+1)}}$
.
Next, we provide the proof of Theorem 2.9. To this end, we recall a definition from [Reference Best and Ferré Moragues4] which is adapted from [Reference Frantzikinakis11].
Definition. [Reference Best and Ferré Moragues4]
We say that a collection of mappings
![]() $a_1,\ldots ,a_k\colon {\mathbb Z}^d \to {\mathbb Z}^d$
is:
$a_1,\ldots ,a_k\colon {\mathbb Z}^d \to {\mathbb Z}^d$
is:
-
(i) good for seminorm estimates for the system
 $(X,\mathcal {B},\mu , (T_n)_{n\in {\mathbb Z}^d})$
along a Følner sequence
$(X,\mathcal {B},\mu , (T_n)_{n\in {\mathbb Z}^d})$
along a Følner sequence
 $(I_N)_{N\in {\mathbb N}}$
of
$(I_N)_{N\in {\mathbb N}}$
of
 ${\mathbb Z}^d$
, if there exists
${\mathbb Z}^d$
, if there exists
 $M\in {\mathbb N}$
such that if
$M\in {\mathbb N}$
such that if
 $f_1,\ldots ,f_k\in L^\infty (\mu )$
and
$f_1,\ldots ,f_k\in L^\infty (\mu )$
and
 $\Vert f_\ell \Vert _{({\mathbb Z}^d)^{\times M}}=0$
for some
$\Vert f_\ell \Vert _{({\mathbb Z}^d)^{\times M}}=0$
for some
 $\ell \in \{1,\ldots ,k\},$
then where the convergence takes place in
$\ell \in \{1,\ldots ,k\},$
then where the convergence takes place in $$ \begin{align*} \lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^\ell T_{a_{i}(n)}f_i=0, \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^\ell T_{a_{i}(n)}f_i=0, \end{align*} $$
 $L^2(\mu );$
$L^2(\mu );$
-
(ii) good for equidistribution for the system
 $(X,\mathcal {B},\mu , (T_n)_{n\in {\mathbb Z}^{d}})$
along a Følner sequence
$(X,\mathcal {B},\mu , (T_n)_{n\in {\mathbb Z}^{d}})$
along a Følner sequence
 $(I_N)_{N\in {\mathbb N}}$
of
$(I_N)_{N\in {\mathbb N}}$
of
 ${\mathbb Z}^{d}$
, if for all
${\mathbb Z}^{d}$
, if for all
 $\alpha _1,\ldots ,\alpha _k\in \text {Spec}((T_{n})_{n\in {\mathbb Z}^{d}}),$
not all of them trivial, we have where
$\alpha _1,\ldots ,\alpha _k\in \text {Spec}((T_{n})_{n\in {\mathbb Z}^{d}}),$
not all of them trivial, we have where $$ \begin{align*} \lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\exp(\alpha_{1}(a_{1}(n))+\cdots+\alpha_{k}(a_{k}(n)))=0, \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\exp(\alpha_{1}(a_{1}(n))+\cdots+\alpha_{k}(a_{k}(n)))=0, \end{align*} $$

Proof of Theorem 2.9
Fix a Følner sequence
![]() $(I_{N})_{N\in {\mathbb N}}$
of
$(I_{N})_{N\in {\mathbb N}}$
of
![]() ${\mathbb Z}^{L}$
. We wish to show that
${\mathbb Z}^{L}$
. We wish to show that
 $$ \begin{align*}\lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^k T_{p_{i}(n)}f_i=\prod_{i=1}^{k}\int_{X}f_{i}\,d\mu\end{align*} $$
$$ \begin{align*}\lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^k T_{p_{i}(n)}f_i=\prod_{i=1}^{k}\int_{X}f_{i}\,d\mu\end{align*} $$
for all
![]() $f_{1},\ldots ,f_{k}\in L^{\infty }(\mu )$
.
$f_{1},\ldots ,f_{k}\in L^{\infty }(\mu )$
.
We first consider the case
![]() $L=d$
to use [Reference Best and Ferré Moragues4, Theorem 3.9]. To this end, it suffices to show that
$L=d$
to use [Reference Best and Ferré Moragues4, Theorem 3.9]. To this end, it suffices to show that
![]() $\mathbf {p}$
is good for seminorm estimates and good for equidistribution.
$\mathbf {p}$
is good for seminorm estimates and good for equidistribution.
Since
![]() $G_{i,j}(\mathbf {p})$
is ergodic for
$G_{i,j}(\mathbf {p})$
is ergodic for
![]() $\mu $
for all
$\mu $
for all
![]() $0\leq i,j\leq k, i\neq j$
, applying Theorem 2.11, we get that
$0\leq i,j\leq k, i\neq j$
, applying Theorem 2.11, we get that
![]() $\mathbf {p}$
is good for seminorm estimates. Moreover,
$\mathbf {p}$
is good for seminorm estimates. Moreover,
![]() $\mathbf {X}$
is an ergodic system.
$\mathbf {X}$
is an ergodic system.
Suppose, for the sake of contradiction, that
![]() $\mathbf {p}$
is not good for equidistribution. Then there exist
$\mathbf {p}$
is not good for equidistribution. Then there exist
![]() $\alpha _{1},\ldots ,\alpha _{k}\in \text {Spec}((T_{n})_{n\in {\mathbb Z}^{d}})$
, not all of them trivial, such that
$\alpha _{1},\ldots ,\alpha _{k}\in \text {Spec}((T_{n})_{n\in {\mathbb Z}^{d}})$
, not all of them trivial, such that
 $$ \begin{align} \lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\exp(\alpha_{1}(p_{1}(n))+\cdots+\alpha_{k}(p_{k}(n)))=c \end{align} $$
$$ \begin{align} \lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\exp(\alpha_{1}(p_{1}(n))+\cdots+\alpha_{k}(p_{k}(n)))=c \end{align} $$
for some
![]() $c\neq 0$
. For
$c\neq 0$
. For
![]() $1\leq i\leq k$
, since
$1\leq i\leq k$
, since
![]() $\alpha _{i} \in \text {Spec}((T_{n})_{n\in {\mathbb Z}^{d}})$
, there exists some non-zero
$\alpha _{i} \in \text {Spec}((T_{n})_{n\in {\mathbb Z}^{d}})$
, there exists some non-zero
![]() $f_{i}\in L^{2}(\mu )$
such that
$f_{i}\in L^{2}(\mu )$
such that
![]() $T_{n}f_{i}=\exp (\alpha _{i}(n))f_{i}$
for all
$T_{n}f_{i}=\exp (\alpha _{i}(n))f_{i}$
for all
![]() $n\in {\mathbb Z}^{d}$
. Since
$n\in {\mathbb Z}^{d}$
. Since
![]() $\mathbf {X}$
is ergodic, we have that
$\mathbf {X}$
is ergodic, we have that
![]() $\vert f_{i}\vert $
is a non-zero constant
$\vert f_{i}\vert $
is a non-zero constant
![]() $\mu $
-almost everywhere. Using equation (34), we have
$\mu $
-almost everywhere. Using equation (34), we have
 $$ \begin{align*} \lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\bigotimes_{i=1}^k T_{p_{i}(n)}f_i=\lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\bigotimes_{i=1}^k \exp(\alpha_{i}(p_{i}(n)))f_i=c\bigotimes_{i=1}^k f_{i}\not\equiv 0. \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\bigotimes_{i=1}^k T_{p_{i}(n)}f_i=\lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\bigotimes_{i=1}^k \exp(\alpha_{i}(p_{i}(n)))f_i=c\bigotimes_{i=1}^k f_{i}\not\equiv 0. \end{align*} $$
However, since at least one of
![]() $\alpha _{1},\ldots ,\alpha _{k}$
is non-trivial, we have that
$\alpha _{1},\ldots ,\alpha _{k}$
is non-trivial, we have that
![]() $\int _{X^{k}}\bigotimes _{i=1}^{k}f_{i}\,d\mu ^{\otimes k} =\prod _{i=1}^{k}\int _{X}f_{i}\,d\mu =0$
, which contradicts condition (ii). Therefore,
$\int _{X^{k}}\bigotimes _{i=1}^{k}f_{i}\,d\mu ^{\otimes k} =\prod _{i=1}^{k}\int _{X}f_{i}\,d\mu =0$
, which contradicts condition (ii). Therefore,
![]() $\mathbf {p}$
is good for equidistribution.
$\mathbf {p}$
is good for equidistribution.
Assume now that
![]() $L<d$
. Let
$L<d$
. Let
![]() $(I^{\prime}_{N})_{N\in {\mathbb N}}$
be the Følner sequence of
$(I^{\prime}_{N})_{N\in {\mathbb N}}$
be the Følner sequence of
![]() ${\mathbb Z}^{d}$
given by
${\mathbb Z}^{d}$
given by
![]() $I^{\prime}_{N}:=I_{N}\times [-N,N]^{d-L}$
. Let
$I^{\prime}_{N}:=I_{N}\times [-N,N]^{d-L}$
. Let
![]() $p^{\prime}_{1},\ldots ,p^{\prime}_{k}\colon {\mathbb Z}^{d}\to {\mathbb Z}^{d}$
be polynomials given by
$p^{\prime}_{1},\ldots ,p^{\prime}_{k}\colon {\mathbb Z}^{d}\to {\mathbb Z}^{d}$
be polynomials given by
![]() $p^{\prime}_{i}(n,m):=p_{i}(n)$
for all
$p^{\prime}_{i}(n,m):=p_{i}(n)$
for all
![]() $n\in {\mathbb Z}^{L}$
and
$n\in {\mathbb Z}^{L}$
and
![]() $m\in {\mathbb Z}^{d-L}$
. Put
$m\in {\mathbb Z}^{d-L}$
. Put
![]() $\mathbf {p}':=(p^{\prime}_{1},\ldots ,p^{\prime}_{k})$
. It is not hard to see that
$\mathbf {p}':=(p^{\prime}_{1},\ldots ,p^{\prime}_{k})$
. It is not hard to see that
![]() $G_{i,j}(\mathbf {p})=G_{i,j}(\mathbf {p}')$
for all
$G_{i,j}(\mathbf {p})=G_{i,j}(\mathbf {p}')$
for all
![]() $0\leq i,j\leq k, i\neq j$
. Moreover, since
$0\leq i,j\leq k, i\neq j$
. Moreover, since
![]() $(T_{p_{1}(n)}\times \cdots \times T_{p_{k}(n)})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{p_{1}(n)}\times \cdots \times T_{p_{k}(n)})_{n\in {\mathbb Z}^{L}}$
is ergodic for
![]() $\mu ^{\otimes k}$
, so is
$\mu ^{\otimes k}$
, so is
![]() $(T_{p^{\prime}_{1}(n)}\times \cdots \times T_{p^{\prime}_{k}(n)})_{n\in {\mathbb Z}^{d}}$
. By the
$(T_{p^{\prime}_{1}(n)}\times \cdots \times T_{p^{\prime}_{k}(n)})_{n\in {\mathbb Z}^{d}}$
. By the
![]() $d=L$
case, we have that
$d=L$
case, we have that
 $$ \begin{align*}\lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^k T_{p_{i}(n)}f_i=\lim_{N\to\infty}\frac{1}{|I^{\prime}_N|}\sum_{n\in I^{\prime}_{N}}\prod_{i=1}^k T_{p^{\prime}_{i}(n)}f_i=\prod_{i=1}^{k}\int_{X}f_{i}\,d\mu.\end{align*} $$
$$ \begin{align*}\lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^k T_{p_{i}(n)}f_i=\lim_{N\to\infty}\frac{1}{|I^{\prime}_N|}\sum_{n\in I^{\prime}_{N}}\prod_{i=1}^k T_{p^{\prime}_{i}(n)}f_i=\prod_{i=1}^{k}\int_{X}f_{i}\,d\mu.\end{align*} $$
Finally, we assume that
![]() $L>d$
. Let
$L>d$
. Let
![]() $(S_{(n,m)})_{n\in {\mathbb Z}^{d},m\in {\mathbb Z}^{L-d}}$
be a
$(S_{(n,m)})_{n\in {\mathbb Z}^{d},m\in {\mathbb Z}^{L-d}}$
be a
![]() ${\mathbb Z}^{L}$
action on
${\mathbb Z}^{L}$
action on
![]() $(X,\mathcal {B},\mu )$
such that
$(X,\mathcal {B},\mu )$
such that
![]() $S_{(n,m)}=T_{n}$
. Let
$S_{(n,m)}=T_{n}$
. Let
![]() $p^{\prime}_{1},\ldots ,p^{\prime}_{k}\colon {\mathbb Z}^{L}\to {\mathbb Z}^{L}$
be polynomials given by
$p^{\prime}_{1},\ldots ,p^{\prime}_{k}\colon {\mathbb Z}^{L}\to {\mathbb Z}^{L}$
be polynomials given by
![]() $p^{\prime}_{i}(n):=(p_{i}(n),0,\ldots ,0)$
for all
$p^{\prime}_{i}(n):=(p_{i}(n),0,\ldots ,0)$
for all
![]() $n\in {\mathbb Z}^{L}$
, where the last
$n\in {\mathbb Z}^{L}$
, where the last
![]() $L-d$
entries are zero. Denote
$L-d$
entries are zero. Denote
![]() $\mathbf {p}':=(p^{\prime}_{1},\ldots ,p^{\prime}_{k})$
. By definition, for all
$\mathbf {p}':=(p^{\prime}_{1},\ldots ,p^{\prime}_{k})$
. By definition, for all
![]() $0\leq i,j\leq k, i\neq j$
, the group
$0\leq i,j\leq k, i\neq j$
, the group
![]() $G_{i,j}(\mathbf {p}')$
consists of elements of the form
$G_{i,j}(\mathbf {p}')$
consists of elements of the form
![]() $(n,0,\ldots ,0)\in {\mathbb Z}^{L}, n\in G_{i,j}(\mathbf {p})$
(with respect to the
$(n,0,\ldots ,0)\in {\mathbb Z}^{L}, n\in G_{i,j}(\mathbf {p})$
(with respect to the
![]() ${\mathbb Z}^{L}$
-system
${\mathbb Z}^{L}$
-system
![]() $(X,\mathcal {B},\mu ,(S_{n})_{n\in {\mathbb Z}^{L}})$
). By the construction of
$(X,\mathcal {B},\mu ,(S_{n})_{n\in {\mathbb Z}^{L}})$
). By the construction of
![]() $(S_{n})_{n\in {\mathbb Z}^{L}}$
, ergodicity of
$(S_{n})_{n\in {\mathbb Z}^{L}}$
, ergodicity of
![]() $G_{i,j}(\mathbf {p})$
with respect to the
$G_{i,j}(\mathbf {p})$
with respect to the
![]() ${\mathbb Z}^{d}$
-system
${\mathbb Z}^{d}$
-system
![]() $(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^{d}})$
implies ergodicity of
$(X,\mathcal {B},\mu ,(T_{n})_{n\in {\mathbb Z}^{d}})$
implies ergodicity of
![]() $G_{i,j}(\mathbf {p}')$
with respect to the
$G_{i,j}(\mathbf {p}')$
with respect to the
![]() ${\mathbb Z}^{L}$
-system
${\mathbb Z}^{L}$
-system
![]() $(X,\mathcal {B},\mu ,(S_{n})_{n\in {\mathbb Z}^{L}})$
. Moreover, since
$(X,\mathcal {B},\mu ,(S_{n})_{n\in {\mathbb Z}^{L}})$
. Moreover, since
![]() $S_{p^{\prime}_{i}(n)}=S_{(p_{i}(n),0,\ldots ,0)}=T_{p_{i}(n)}$
for all
$S_{p^{\prime}_{i}(n)}=S_{(p_{i}(n),0,\ldots ,0)}=T_{p_{i}(n)}$
for all
![]() $n\in {\mathbb Z}^{L}$
, we have that
$n\in {\mathbb Z}^{L}$
, we have that
![]() $(S_{p^{\prime}_{1}(n)}\times \cdots \times S_{p^{\prime}_{k}(n)})_{n\in {\mathbb Z}^{L}}=(T_{p_{1}(n)}\times \cdots \times T_{p_{k}(n)})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(S_{p^{\prime}_{1}(n)}\times \cdots \times S_{p^{\prime}_{k}(n)})_{n\in {\mathbb Z}^{L}}=(T_{p_{1}(n)}\times \cdots \times T_{p_{k}(n)})_{n\in {\mathbb Z}^{L}}$
is ergodic for
![]() $\mu ^{\otimes k}$
. By the
$\mu ^{\otimes k}$
. By the
![]() $d=L$
case, we have that
$d=L$
case, we have that
 $$ \begin{align*}\lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^k T_{p_{i}(n)}f_i=\lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^k S_{p^{\prime}_{i}(n)}f_i=\prod_{i=1}^{k}\int_{X}f_{i}\,d\mu, \end{align*} $$
$$ \begin{align*}\lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^k T_{p_{i}(n)}f_i=\lim_{N\to\infty}\frac{1}{|I_N|}\sum_{n\in I_{N}}\prod_{i=1}^k S_{p^{\prime}_{i}(n)}f_i=\prod_{i=1}^{k}\int_{X}f_{i}\,d\mu, \end{align*} $$
which completes the proof.
Finally, we prove Theorem 2.5. We start by proving that condition (C1) implies condition (C2). In fact, we show the following more general result.
Proposition 6.2. Let
![]() $d,k,L\in \mathbb {N}, q_{1},\ldots , q_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be polynomials, and
$d,k,L\in \mathbb {N}, q_{1},\ldots , q_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}^{d}$
be polynomials, and
![]() $\mathbf {X}=(X,\mathcal {B},\mu , (T_{g})_{g\in \mathbb {Z}^{d}})$
be a
$\mathbf {X}=(X,\mathcal {B},\mu , (T_{g})_{g\in \mathbb {Z}^{d}})$
be a
![]() $\mathbb {Z}^{d}$
-system. Suppose that
$\mathbb {Z}^{d}$
-system. Suppose that
![]() $(T_{q_{1}(n)},\ldots ,T_{q_{k}(n)})_{n\in {\mathbb Z}^{L}}$
is jointly ergodic for
$(T_{q_{1}(n)},\ldots ,T_{q_{k}(n)})_{n\in {\mathbb Z}^{L}}$
is jointly ergodic for
![]() $\mu $
. Then for all
$\mu $
. Then for all
![]() $1\leq i,j\leq k, i\neq j$
, we have that
$1\leq i,j\leq k, i\neq j$
, we have that
![]() $(T_{q_{i}(n)-q_{j}(n)})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{q_{i}(n)-q_{j}(n)})_{n\in {\mathbb Z}^{L}}$
is ergodic for
![]() $\mu $
.
$\mu $
.
Furthermore, if there exist polynomials
![]() $p_{1},\ldots , p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}$
and
$p_{1},\ldots , p_{k}\colon \mathbb {Z}^{L}\to \mathbb {Z}$
and
![]() $v_{1},\ldots ,v_{k}\in {\mathbb Z}^{d}$
such that
$v_{1},\ldots ,v_{k}\in {\mathbb Z}^{d}$
such that
![]() $q_{i}(n)=p_{i}(n)v_{i}$
for all
$q_{i}(n)=p_{i}(n)v_{i}$
for all
![]() $1\leq i\leq k$
, then
$1\leq i\leq k$
, then
![]() $(T_{p_{1}(n)v_{1}}\times \cdots \times T_{p_{k}(n)v_{k}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{p_{1}(n)v_{1}}\times \cdots \times T_{p_{k}(n)v_{k}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
![]() $\mu ^{\otimes k}$
.
$\mu ^{\otimes k}$
.
Proof. The sequence
![]() $(T_{q_{i}(n)-q_{j}(n)})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{q_{i}(n)-q_{j}(n)})_{n\in {\mathbb Z}^{L}}$
is ergodic for
![]() $\mu $
for all
$\mu $
for all
![]() $1\leq i\neq j\leq k$
by an argument similar to that given in the proof of [Reference Donoso, Koutsogiannis and Sun7, Proposition 5.3], so we choose to omit the details.
$1\leq i\neq j\leq k$
by an argument similar to that given in the proof of [Reference Donoso, Koutsogiannis and Sun7, Proposition 5.3], so we choose to omit the details.
We now assume that
![]() $q_{i}(n)=p_{i}(n)v_{i}$
for all
$q_{i}(n)=p_{i}(n)v_{i}$
for all
![]() $1\leq i\leq k$
and show that
$1\leq i\leq k$
and show that
![]() $(T_{p_{1}(n)v_{1}}\times \cdots \times T_{p_{k}(n)v_{k}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{p_{1}(n)v_{1}}\times \cdots \times T_{p_{k}(n)v_{k}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
![]() $\mu ^{\otimes k}$
. It suffices to show that for all
$\mu ^{\otimes k}$
. It suffices to show that for all
![]() $f_{i}\in L^{\infty }(\mu ),1\leq i\leq k$
with
$f_{i}\in L^{\infty }(\mu ),1\leq i\leq k$
with
![]() $\prod _{i=1}^{k} \int _{X}f_{i}\,d\mu =0$
, we have that
$\prod _{i=1}^{k} \int _{X}f_{i}\,d\mu =0$
, we have that
 $$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \bigg\Vert\mathbb{E}_{n\in I_{N}}\bigotimes_{i=1}^{k}T_{p_{i}(n)v_{i}}f_{i}\bigg\Vert_{L^{2}(\mu^{\otimes k})}=0. \end{align} $$
$$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty} \bigg\Vert\mathbb{E}_{n\in I_{N}}\bigotimes_{i=1}^{k}T_{p_{i}(n)v_{i}}f_{i}\bigg\Vert_{L^{2}(\mu^{\otimes k})}=0. \end{align} $$
Claim. If
![]() $\mathbb {E}(f_{i}\vert Z_{{\mathbb Z}^{d},{\mathbb Z}^{d}}(\mathbf {X}))=0$
for some
$\mathbb {E}(f_{i}\vert Z_{{\mathbb Z}^{d},{\mathbb Z}^{d}}(\mathbf {X}))=0$
for some
![]() $1\leq i\leq k$
, then equation (35) holds.
$1\leq i\leq k$
, then equation (35) holds.
Proof of the claim
We may assume without loss of generality that
![]() $\deg (p_{1})\geq \deg (p_{2})\geq \cdots \geq \deg (p_{k})$
. Suppose that we have shown that for some
$\deg (p_{1})\geq \deg (p_{2})\geq \cdots \geq \deg (p_{k})$
. Suppose that we have shown that for some
![]() $1\leq k_{0}\leq k$
, equation (35) holds if
$1\leq k_{0}\leq k$
, equation (35) holds if
![]() $\mathbb {E}(f_{i}\vert Z_{{\mathbb Z}^{d},{\mathbb Z}^{d}}(\mathbf {X}))=0$
for some
$\mathbb {E}(f_{i}\vert Z_{{\mathbb Z}^{d},{\mathbb Z}^{d}}(\mathbf {X}))=0$
for some
![]() $1\leq i\leq k_{0}-1$
, where the case
$1\leq i\leq k_{0}-1$
, where the case
![]() $k_{0}=1$
is understood to be always true. It suffices to show that equation (35) holds if
$k_{0}=1$
is understood to be always true. It suffices to show that equation (35) holds if
![]() $\mathbb {E}(f_{k_{0}}\vert Z_{{\mathbb Z}^{d},{\mathbb Z}^{d}}(\mathbf {X}))=0$
.
$\mathbb {E}(f_{k_{0}}\vert Z_{{\mathbb Z}^{d},{\mathbb Z}^{d}}(\mathbf {X}))=0$
.
By the induction hypothesis, we may assume without loss of generality that
![]() $f_{i}$
is
$f_{i}$
is
![]() $Z_{{\mathbb Z}^{d},{\mathbb Z}^{d}}(\mathbf {X})$
-measurable for all
$Z_{{\mathbb Z}^{d},{\mathbb Z}^{d}}(\mathbf {X})$
-measurable for all
![]() $1\leq i\leq k_{0}-1$
. By [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.7], we can approximate each
$1\leq i\leq k_{0}-1$
. By [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.7], we can approximate each
![]() $f_{i}$
in
$f_{i}$
in
![]() $L^{2}(\mu )$
by an eigenfunction of
$L^{2}(\mu )$
by an eigenfunction of
![]() $\mathbf {X}$
. By multi-linearity, we may assume without loss of generality that each
$\mathbf {X}$
. By multi-linearity, we may assume without loss of generality that each
![]() $f_{i},1\leq i\leq k_{0}-1,$
is a non-constant eigenfunction of
$f_{i},1\leq i\leq k_{0}-1,$
is a non-constant eigenfunction of
![]() $\mathbf {X}$
given by
$\mathbf {X}$
given by
![]() $T_{n}f_{i}=\exp (\lambda _{i}(n))f_{i}$
for all
$T_{n}f_{i}=\exp (\lambda _{i}(n))f_{i}$
for all
![]() $n\in \mathbb {Z}^{d}$
and some group homomorphism
$n\in \mathbb {Z}^{d}$
and some group homomorphism
![]() $\lambda _{i}\colon \mathbb {Z}^{d}\to {\mathbb R}$
, with
$\lambda _{i}\colon \mathbb {Z}^{d}\to {\mathbb R}$
, with
![]() $f_{i}(x)\neq 0\ \mu $
-almost every
$f_{i}(x)\neq 0\ \mu $
-almost every
![]() $x\in X$
. Then, the left-hand side of equation (35) is equal to
$x\in X$
. Then, the left-hand side of equation (35) is equal to
 $$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\Vert\mathbb{E}_{n\in I_{N}}\exp(P(n))\bigotimes_{i=1}^{k_{0}-1}f_{i}\bigotimes_{i=k_{0}}^{k}T_{p_{i}(n)v_{i}}f_{i}\bigg\Vert_{L^{2}(\mu^{\otimes k})}, \end{align} $$
$$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\Vert\mathbb{E}_{n\in I_{N}}\exp(P(n))\bigotimes_{i=1}^{k_{0}-1}f_{i}\bigotimes_{i=k_{0}}^{k}T_{p_{i}(n)v_{i}}f_{i}\bigg\Vert_{L^{2}(\mu^{\otimes k})}, \end{align} $$
where ![]() Denote
Denote
![]() $P(n)=\sum _{j=0}^{\deg (p_{1})}Q_{j}(n)$
, where
$P(n)=\sum _{j=0}^{\deg (p_{1})}Q_{j}(n)$
, where
![]() $Q_{j}$
is a homogeneous polynomial of degree j for all
$Q_{j}$
is a homogeneous polynomial of degree j for all
![]() $0\leq j\leq \deg (p_{1})$
. Then
$0\leq j\leq \deg (p_{1})$
. Then
 $$ \begin{align} \Delta^{K}P(n,h_{1},\ldots,h_{K})=\sum_{j=K}^{\deg(p_{1})}\Delta^{K}Q_{j}(n,h_{1},\ldots,h_{K}). \end{align} $$
$$ \begin{align} \Delta^{K}P(n,h_{1},\ldots,h_{K})=\sum_{j=K}^{\deg(p_{1})}\Delta^{K}Q_{j}(n,h_{1},\ldots,h_{K}). \end{align} $$
We first consider the case where
![]() $Q_{j}(n)\notin \mathbb {Q}[n]$
for some
$Q_{j}(n)\notin \mathbb {Q}[n]$
for some
![]() $\deg (p_{k_{0}})+1\leq j\leq \deg (p_{1})$
. In this case, let
$\deg (p_{k_{0}})+1\leq j\leq \deg (p_{1})$
. In this case, let
![]() $K=\deg (p_{k_{0}})$
in equation (37). Since
$K=\deg (p_{k_{0}})$
in equation (37). Since
![]() $\Delta ^{K}p_{i}(n,h_{1},\ldots ,h_{K})$
is constant in n for all
$\Delta ^{K}p_{i}(n,h_{1},\ldots ,h_{K})$
is constant in n for all
![]() $k_{0}\leq i\leq k$
, by Lemma 4.3, to show that equation (36) is 0, it suffices to show that
$k_{0}\leq i\leq k$
, by Lemma 4.3, to show that equation (36) is 0, it suffices to show that
 $$ \begin{align} {\overline{\mathbb{E}}}^{\square}_{h_{1},\ldots,h_{K}\in{\mathbb Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\vert\mathbb{E}_{n\in I_{N}}\exp(\Delta^{K}P(n,h_{1},\ldots,h_{K}))\vert=0 \end{align} $$
$$ \begin{align} {\overline{\mathbb{E}}}^{\square}_{h_{1},\ldots,h_{K}\in{\mathbb Z}^{L}}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\vert\mathbb{E}_{n\in I_{N}}\exp(\Delta^{K}P(n,h_{1},\ldots,h_{K}))\vert=0 \end{align} $$
(see Definition 3.13 for the definition of the polynomial
![]() $\Delta ^{K}P$
).
$\Delta ^{K}P$
).
As
![]() $Q_{j}(n)\notin \mathbb {Q}[n]$
for some
$Q_{j}(n)\notin \mathbb {Q}[n]$
for some
![]() $\deg (p_{k_{0}})+1\leq j\leq \deg (p_{1})$
, Lemma 3.14 implies that
$\deg (p_{k_{0}})+1\leq j\leq \deg (p_{1})$
, Lemma 3.14 implies that
![]() $\Delta ^{K}Q_{j}(\cdot ,h_{1}, \ldots ,h_{K})\notin \mathbb {Q}[n]$
for a set of
$\Delta ^{K}Q_{j}(\cdot ,h_{1}, \ldots ,h_{K})\notin \mathbb {Q}[n]$
for a set of
![]() $(h_{1},\ldots ,h_{K})$
of density 1. By Weyl’s criterion and equation (37), we have that equation (38) holds and thus equation (35) holds.
$(h_{1},\ldots ,h_{K})$
of density 1. By Weyl’s criterion and equation (37), we have that equation (38) holds and thus equation (35) holds.
We now consider the case where
![]() $Q_{j}(n)\in \mathbb {Q}[n]$
for all
$Q_{j}(n)\in \mathbb {Q}[n]$
for all
![]() $K+1\leq j\leq \deg (p_{1})$
. Let
$K+1\leq j\leq \deg (p_{1})$
. Let
![]() $P'(n)=\sum _{j=0}^{K}Q_{j}(n)$
. It is not hard to see that there exists
$P'(n)=\sum _{j=0}^{K}Q_{j}(n)$
. It is not hard to see that there exists
![]() $Q\in {\mathbb N}$
such that for all
$Q\in {\mathbb N}$
such that for all
![]() $r\in \{0,\ldots ,Q-1\}^{L}$
and
$r\in \{0,\ldots ,Q-1\}^{L}$
and
![]() $n\in \mathbb {Z}^{L}$
, we have that
$n\in \mathbb {Z}^{L}$
, we have that
By equation (36), to show equation (35), it suffices to show that for all
![]() $r\in \{0,\ldots , Q-1\}^{L}$
, we have that
$r\in \{0,\ldots , Q-1\}^{L}$
, we have that
 $$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\Vert\mathbb{E}_{n\in I_{N}}\exp(P'(Qn+r))\bigotimes_{i=k_{0}}^{k}T_{p_{i}(Qn+r)v_{i}}f_{i}\bigg\Vert_{L^{2}(\mu^{\otimes t})}=0, \end{align} $$
$$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\bigg\Vert\mathbb{E}_{n\in I_{N}}\exp(P'(Qn+r))\bigotimes_{i=k_{0}}^{k}T_{p_{i}(Qn+r)v_{i}}f_{i}\bigg\Vert_{L^{2}(\mu^{\otimes t})}=0, \end{align} $$
where
![]() $t=k-k_{0}+1$
. Fix
$t=k-k_{0}+1$
. Fix
![]() $r\in \{0,\ldots ,Q-1\}^{L}$
and set
$r\in \{0,\ldots ,Q-1\}^{L}$
and set
![]() $R(n)=P'(Qn+r)$
. Let
$R(n)=P'(Qn+r)$
. Let
![]() $p\colon {\mathbb Z}^{L}\to {\mathbb Z}^{dt}$
be the polynomial given by
$p\colon {\mathbb Z}^{L}\to {\mathbb Z}^{dt}$
be the polynomial given by
Let
![]() $(X^{t},\mathcal {B}^{t},\mu ^{t},(S_{g})_{g\in {\mathbb Z}^{dt}})$
be the
$(X^{t},\mathcal {B}^{t},\mu ^{t},(S_{g})_{g\in {\mathbb Z}^{dt}})$
be the
![]() ${\mathbb Z}^{dt}$
-system such that
${\mathbb Z}^{dt}$
-system such that

for all
![]() $u_{i}\in {\mathbb Z}^{d}, k_{0}\leq i\leq k$
, and denote
$u_{i}\in {\mathbb Z}^{d}, k_{0}\leq i\leq k$
, and denote ![]() . We may then rewrite the left-hand side of equation (39) as
. We may then rewrite the left-hand side of equation (39) as
 $$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}}\exp(R(n))S_{p(n)}f\Vert_{L^{2}(\mu^{\otimes t})}. \end{align} $$
$$ \begin{align} {\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}}\exp(R(n))S_{p(n)}f\Vert_{L^{2}(\mu^{\otimes t})}. \end{align} $$
For
![]() $K=\deg (p_{k_{0}})-1,$
to show that equation (40) is zero, it suffices, by Lemma 4.3, to show
$K=\deg (p_{k_{0}})-1,$
to show that equation (40) is zero, it suffices, by Lemma 4.3, to show
 $$ \begin{align} {\overline{\mathbb{E}}}^{\square}_{\mathbf{{h}}=(h_{1},\ldots,h_{K})\in({\mathbb Z}^{L})^K}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}}\exp(\Delta^{K}R(n,\mathbf{ {h}}))S_{\Delta^{K}p(n,\mathbf{{h}})}f\Vert_{L^{2}(\mu^{\otimes t})}=0. \end{align} $$
$$ \begin{align} {\overline{\mathbb{E}}}^{\square}_{\mathbf{{h}}=(h_{1},\ldots,h_{K})\in({\mathbb Z}^{L})^K}{\sup_{\substack{ (I_{N})_{N\in\mathbb{N}} \\ \mathrm{ F\unicode{xf8} lner\, seq.} }}}\varlimsup_{N\to \infty}\Vert\mathbb{E}_{n\in I_{N}}\exp(\Delta^{K}R(n,\mathbf{ {h}}))S_{\Delta^{K}p(n,\mathbf{{h}})}f\Vert_{L^{2}(\mu^{\otimes t})}=0. \end{align} $$
By assumption,
![]() $\Delta ^{K}R(n,h_{1},\ldots ,h_{K})$
is of degree 1 in the variable n. Since
$\Delta ^{K}R(n,h_{1},\ldots ,h_{K})$
is of degree 1 in the variable n. Since
![]() $\deg (p)=\deg (p_{k_{0}})\geq \deg (p_{i})$
for all
$\deg (p)=\deg (p_{k_{0}})\geq \deg (p_{i})$
for all
![]() $i\geq k_{0}$
,
$i\geq k_{0}$
,
![]() $\Delta ^{K} p(n,h_{1},\ldots ,h_{K})$
is also of degree 1 in the variable n. We may thus assume that
$\Delta ^{K} p(n,h_{1},\ldots ,h_{K})$
is also of degree 1 in the variable n. We may thus assume that
for some polynomials
![]() $c_{k_{0}},\ldots ,c_{k}\colon {\mathbb Z}^{LK}\to {\mathbb Z}^{L}$
and
$c_{k_{0}},\ldots ,c_{k}\colon {\mathbb Z}^{LK}\to {\mathbb Z}^{L}$
and
![]() $c^{\prime}_{k_{0}},\ldots ,c^{\prime}_{k}\colon {\mathbb Z}^{LK}\to {\mathbb Z}$
. Write
$c^{\prime}_{k_{0}},\ldots ,c^{\prime}_{k}\colon {\mathbb Z}^{LK}\to {\mathbb Z}$
. Write ![]() (which is viewed as a t-tuple of L-tuple of vectors in
(which is viewed as a t-tuple of L-tuple of vectors in
![]() ${\mathbb Z}^{d}$
). If we write
${\mathbb Z}^{d}$
). If we write
for some
![]() $c_{i,j}(h_{1},\ldots , h_{K})\in {\mathbb Z}$
, then, by definition,
$c_{i,j}(h_{1},\ldots , h_{K})\in {\mathbb Z}$
, then, by definition,
![]() $G({\mathbf {c}}(h_{1},\ldots ,h_K))$
is the subgroup of
$G({\mathbf {c}}(h_{1},\ldots ,h_K))$
is the subgroup of
![]() ${\mathbb Z}^{dt}$
generated by the elements
${\mathbb Z}^{dt}$
generated by the elements
By Lemma 4.4, the left-hand side of equation (41) is bounded by a constant multiple of
where
![]() $G(c_{k_{0}}(h_{1},\ldots ,h_K)v_{k_{0}})$
is the subgroup of
$G(c_{k_{0}}(h_{1},\ldots ,h_K)v_{k_{0}})$
is the subgroup of
![]() ${\mathbb Z}^{d}$
generated by the elements
${\mathbb Z}^{d}$
generated by the elements
that is, the entries of
![]() $c_{k_{0}}(h_{1},\ldots ,h_{K})v_{k_{0}}$
. For any
$c_{k_{0}}(h_{1},\ldots ,h_{K})v_{k_{0}}$
. For any
![]() $u_{k_{0}}\in G(c_{k_{0}}(h_{1},\ldots ,h_{K})v_{k_{0}})$
, note that
$u_{k_{0}}\in G(c_{k_{0}}(h_{1},\ldots ,h_{K})v_{k_{0}})$
, note that
![]() $u_{k_{0}}$
is a rational multiple of
$u_{k_{0}}$
is a rational multiple of
![]() $v_{k_{0}}$
. So, if
$v_{k_{0}}$
. So, if
![]() $c_{k_{0}}(h_{1},\ldots ,h_{K})\neq \mathbf {0}$
, then
$c_{k_{0}}(h_{1},\ldots ,h_{K})\neq \mathbf {0}$
, then
![]() $G(c_{k_{0}}(h_{1},\ldots ,h_{K})v_{k_{0}})=G(v_{k_{0}})$
.
$G(c_{k_{0}}(h_{1},\ldots ,h_{K})v_{k_{0}})=G(v_{k_{0}})$
.
Since
![]() $(T_{p_{i}(n)v_{i}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{p_{i}(n)v_{i}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
![]() $\mu $
, we have that
$\mu $
, we have that
![]() $T_{v_{i}}$
is ergodic for
$T_{v_{i}}$
is ergodic for
![]() $\mu $
. As
$\mu $
. As
![]() $\mathbb {E}(f_{k_{0}}\vert Z_{{\mathbb Z}^{d},{\mathbb Z}^{d}}(\mathbf {X}))=0$
, by [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.4], we have that
$\mathbb {E}(f_{k_{0}}\vert Z_{{\mathbb Z}^{d},{\mathbb Z}^{d}}(\mathbf {X}))=0$
, by [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.4], we have that
whenever
![]() $c_{k_{0}}(h_{1},\ldots ,h_{K})\neq \mathbf {0}$
. Since
$c_{k_{0}}(h_{1},\ldots ,h_{K})\neq \mathbf {0}$
. Since
![]() $K=\deg (p_{k_{0}})-1=\deg (p_{k_{0}}(Q\cdot +r))-1$
, it is easy to see that
$K=\deg (p_{k_{0}})-1=\deg (p_{k_{0}}(Q\cdot +r))-1$
, it is easy to see that
![]() $c_{k_{0}}\not \equiv \mathbf {0}$
. By [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.11], the set of such
$c_{k_{0}}\not \equiv \mathbf {0}$
. By [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.11], the set of such
![]() $(h_{1},\ldots ,h_{K})$
is of density 1. So, averaging over all
$(h_{1},\ldots ,h_{K})$
is of density 1. So, averaging over all
![]() $h_{1},\ldots ,h_{K}\in {\mathbb Z}^{L}$
, we have that equation (42) is 0. This finishes the proof of the claim.
$h_{1},\ldots ,h_{K}\in {\mathbb Z}^{L}$
, we have that equation (42) is 0. This finishes the proof of the claim.
Using the claim, it suffices to prove equation (35) under the assumption that all
![]() $f_{i}$
terms are measurable with respect to
$f_{i}$
terms are measurable with respect to
![]() $Z_{({\mathbb Z}^{d})^{\times 2}}(\mathbf {X})$
. By [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.7], we can approximate each
$Z_{({\mathbb Z}^{d})^{\times 2}}(\mathbf {X})$
. By [Reference Donoso, Koutsogiannis and Sun7, Lemma 2.7], we can approximate each
![]() $f_{i}$
in
$f_{i}$
in
![]() $L^{2}(\mu )$
by an eigenfunction of
$L^{2}(\mu )$
by an eigenfunction of
![]() $\mathbf {X}$
. By multilinearity, we may assume without loss of generality that each
$\mathbf {X}$
. By multilinearity, we may assume without loss of generality that each
![]() $f_{i}$
is a non-constant eigenfunction of
$f_{i}$
is a non-constant eigenfunction of
![]() $\mathbf {X}$
satisfying
$\mathbf {X}$
satisfying
![]() $T_{n}f_{i}=\exp (\lambda _{i}(n))f_{i}$
for all
$T_{n}f_{i}=\exp (\lambda _{i}(n))f_{i}$
for all
![]() $n\in \mathbb {Z}^{d},$
for some group homomorphism
$n\in \mathbb {Z}^{d},$
for some group homomorphism
![]() $\lambda _{i}\colon \mathbb {Z}^{d}\to {\mathbb R},$
with
$\lambda _{i}\colon \mathbb {Z}^{d}\to {\mathbb R},$
with
![]() $f_{i}(x)\neq 0\ \mu $
-almost every
$f_{i}(x)\neq 0\ \mu $
-almost every
![]() $x\in X$
. Then, since
$x\in X$
. Then, since
![]() $(T_{p_{i}(n)v_{i}}\colon 1\leq i\leq k)_{n\in {\mathbb Z}^{L}}$
is jointly ergodic for
$(T_{p_{i}(n)v_{i}}\colon 1\leq i\leq k)_{n\in {\mathbb Z}^{L}}$
is jointly ergodic for
![]() $\mu $
, for any Følner sequence
$\mu $
, for any Følner sequence
![]() $(I_{N})_{N\in {\mathbb N}}$
of
$(I_{N})_{N\in {\mathbb N}}$
of
![]() ${\mathbb Z}^{d}$
,
${\mathbb Z}^{d}$
,
 $$ \begin{align*} 0&= \prod_{i=1}^{k}\int_{X} f_{i}\, d\mu= \lim_{N\to\infty}\mathbb{E}_{n\in I_{N}}\prod_{i=1}^{k}T_{p_{i}(n)v_{i}}f_{i} \\ & =\bigg(\lim_{N\to\infty}\mathbb{E}_{n\in I_{N}}\prod_{i=1}^{k}\exp(\lambda_{i}(p_{i}(n)v_{i}))\bigg)\prod_{i=1}^{k}f_{i}. \end{align*} $$
$$ \begin{align*} 0&= \prod_{i=1}^{k}\int_{X} f_{i}\, d\mu= \lim_{N\to\infty}\mathbb{E}_{n\in I_{N}}\prod_{i=1}^{k}T_{p_{i}(n)v_{i}}f_{i} \\ & =\bigg(\lim_{N\to\infty}\mathbb{E}_{n\in I_{N}}\prod_{i=1}^{k}\exp(\lambda_{i}(p_{i}(n)v_{i}))\bigg)\prod_{i=1}^{k}f_{i}. \end{align*} $$
This implies that
![]() $\lim _{N\to \infty }\mathbb {E}_{n\in I_{N}}\prod _{i=1}^{k}\exp (\lambda _{i}(p_{i}(n)v_{i}))=0,$
so,
$\lim _{N\to \infty }\mathbb {E}_{n\in I_{N}}\prod _{i=1}^{k}\exp (\lambda _{i}(p_{i}(n)v_{i}))=0,$
so,
 $$ \begin{align*}\lim_{N\to\infty}\mathbb{E}_{n\in I_{N}}\bigotimes_{i=1}^{k} T_{p_{i}(n)v_{i}}f_{i}=\bigg(\lim_{N\to\infty}\mathbb{E}_{n\in I_{N}}\prod_{i=1}^{k}\exp(\lambda_{i}(p_{i}(n)v_{i}))\bigg)\bigotimes_{i=1}^{k}f_{i}.\end{align*} $$
$$ \begin{align*}\lim_{N\to\infty}\mathbb{E}_{n\in I_{N}}\bigotimes_{i=1}^{k} T_{p_{i}(n)v_{i}}f_{i}=\bigg(\lim_{N\to\infty}\mathbb{E}_{n\in I_{N}}\prod_{i=1}^{k}\exp(\lambda_{i}(p_{i}(n)v_{i}))\bigg)\bigotimes_{i=1}^{k}f_{i}.\end{align*} $$
This finishes the proof.
We are now ready to complete the proof of Theorem 2.5.
Proof of Theorem 2.5
Using Proposition 6.2, we have that condition (C1) implies condition (C2). It is obvious that condition (C2) implies condition (C2’). So, it suffices to show that condition (C2’) implies condition (C1).
It is not hard to see that we may assume without loss of generality that
![]() $p_{i}(0)=0$
for all
$p_{i}(0)=0$
for all
![]() $1\leq i\leq k$
. By Theorem 2.9, to show that
$1\leq i\leq k$
. By Theorem 2.9, to show that
![]() $(T_{p_{i}(n)v_{i}}\colon 1\leq i\leq k)_{n\in {\mathbb Z}^{L}}$
is jointly ergodic for
$(T_{p_{i}(n)v_{i}}\colon 1\leq i\leq k)_{n\in {\mathbb Z}^{L}}$
is jointly ergodic for
![]() $\mu $
, it suffices to show that
$\mu $
, it suffices to show that
![]() $G_{i,j}(\mathbf {p})$
is ergodic for
$G_{i,j}(\mathbf {p})$
is ergodic for
![]() $\mu $
for all
$\mu $
for all
![]() $0\leq i,j\leq k, i\neq j$
. Fix any such pair
$0\leq i,j\leq k, i\neq j$
. Fix any such pair
![]() $(i,j)$
. We may assume without loss of generality that
$(i,j)$
. We may assume without loss of generality that
![]() $i\neq 0$
. If
$i\neq 0$
. If
![]() $j=0$
, then by subcondition (ii),
$j=0$
, then by subcondition (ii),
![]() $(T_{p_{i}(n)v_{i}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{p_{i}(n)v_{i}})_{n\in {\mathbb Z}^{L}}$
is ergodic for
![]() $\mu $
. So,
$\mu $
. So,
![]() $T_{v_{i}}$
is ergodic for
$T_{v_{i}}$
is ergodic for
![]() $\mu $
, and thus
$\mu $
, and thus
![]() $G_{i,0}(\mathbf {p})=G(v_{i})$
is ergodic for
$G_{i,0}(\mathbf {p})=G(v_{i})$
is ergodic for
![]() $\mu $
. Hence, we may now assume that
$\mu $
. Hence, we may now assume that
![]() $j\neq 0$
.
$j\neq 0$
.
Assume first that
![]() $\deg (p_{i})=\deg (p_{j})$
. By assumption, either
$\deg (p_{i})=\deg (p_{j})$
. By assumption, either
![]() $v_{i}$
and
$v_{i}$
and
![]() $v_{j}$
are linearly dependent, or
$v_{j}$
are linearly dependent, or
![]() $p_{i}$
and
$p_{i}$
and
![]() $p_{j}$
are linearly dependent.
$p_{j}$
are linearly dependent.
If
![]() $v_{i}$
and
$v_{i}$
and
![]() $v_{j}$
are linearly dependent over
$v_{j}$
are linearly dependent over
![]() ${\mathbb Z}$
, then we may assume without loss of generality that
${\mathbb Z}$
, then we may assume without loss of generality that
![]() $v_{i}=av$
and
$v_{i}=av$
and
![]() $v_{j}=bv$
for some
$v_{j}=bv$
for some
![]() $a,b\in \mathbb {Q}$
and
$a,b\in \mathbb {Q}$
and
![]() $v\in {\mathbb Z}^{d}$
. By subcondition (i),
$v\in {\mathbb Z}^{d}$
. By subcondition (i),
![]() $(T_{(ap_{i}(n)-bp_{j}(n))v})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{(ap_{i}(n)-bp_{j}(n))v})_{n\in {\mathbb Z}^{L}}$
is ergodic for
![]() $\mu $
, which implies that
$\mu $
, which implies that
![]() $G(v)$
is ergodic for
$G(v)$
is ergodic for
![]() $\mu $
. However,
$\mu $
. However,
![]() $G_{i,j}(\mathbf {p})$
is a group generated by some elements which are linear combinations of
$G_{i,j}(\mathbf {p})$
is a group generated by some elements which are linear combinations of
![]() $v_{i}$
and
$v_{i}$
and
![]() $v_{j}$
, thus multiples of v. Since
$v_{j}$
, thus multiples of v. Since
![]() $\mathbf {p}$
is non-degenerate,
$\mathbf {p}$
is non-degenerate,
![]() $G_{i,j}(\mathbf {p})$
is not the trivial group. It follows that
$G_{i,j}(\mathbf {p})$
is not the trivial group. It follows that
![]() $G_{i,j}(\mathbf {p})=G(v),$
so the group
$G_{i,j}(\mathbf {p})=G(v),$
so the group
![]() $G_{i,j}(\mathbf {p})$
is ergodic for
$G_{i,j}(\mathbf {p})$
is ergodic for
![]() $\mu $
.
$\mu $
.
If
![]() $p_{i}$
and
$p_{i}$
and
![]() $p_{j}$
are linearly dependent over
$p_{j}$
are linearly dependent over
![]() ${\mathbb Z}$
, then we may assume without loss of generality that
${\mathbb Z}$
, then we may assume without loss of generality that
![]() $p_{i}=ap$
and
$p_{i}=ap$
and
![]() $p_{j}=bp$
for some
$p_{j}=bp$
for some
![]() $a,b\in \mathbb {Q}$
and polynomial p. By subcondition (i),
$a,b\in \mathbb {Q}$
and polynomial p. By subcondition (i),
![]() $(T_{(p(n)(av_{i}-bv_{j})})_{n\in {\mathbb Z}^{L}}$
is ergodic for
$(T_{(p(n)(av_{i}-bv_{j})})_{n\in {\mathbb Z}^{L}}$
is ergodic for
![]() $\mu $
, which implies that
$\mu $
, which implies that
![]() $G(av_{i}-bv_{j})$
is ergodic for
$G(av_{i}-bv_{j})$
is ergodic for
![]() $\mu $
. However,
$\mu $
. However,
![]() $G_{i,j}(\mathbf {p})$
is a group generated by some elements which are multiples of
$G_{i,j}(\mathbf {p})$
is a group generated by some elements which are multiples of
![]() $av_{i}-bv_{j}$
. Since
$av_{i}-bv_{j}$
. Since
![]() $\mathbf {p}$
is non-degenerate,
$\mathbf {p}$
is non-degenerate,
![]() $G_{i,j}(\mathbf {p})$
is not the trivial group. It follows that
$G_{i,j}(\mathbf {p})$
is not the trivial group. It follows that
![]() $G_{i,j}(\mathbf {p})=G(av_{i}-bv_{j}),$
so the group
$G_{i,j}(\mathbf {p})=G(av_{i}-bv_{j}),$
so the group
![]() $G_{i,j}(\mathbf {p})$
is ergodic for
$G_{i,j}(\mathbf {p})$
is ergodic for
![]() $\mu $
.
$\mu $
.
Finally, we consider the case when
![]() $\deg (p_{i})\neq \deg (p_{j})$
. We may further assume without loss of generality that
$\deg (p_{i})\neq \deg (p_{j})$
. We may further assume without loss of generality that
![]() $\deg (p_{i})>\deg (p_{j})$
. In this case,
$\deg (p_{i})>\deg (p_{j})$
. In this case,
![]() $G_{i,j}(\mathbf {p})=G_{i,0}(\mathbf {p})$
, which we have shown is ergodic for
$G_{i,j}(\mathbf {p})=G_{i,0}(\mathbf {p})$
, which we have shown is ergodic for
![]() $\mu $
.
$\mu $
.
7 Potential future directions
We close this article with two potential future directions regarding the splitting of multicorrelation sequences. The first one is for integer polynomial iterates under no assumptions on the transformations other than commutativity (see Theorem 7.1 for a special case of two terms).
The second one pertains to potential results analogous to Theorem 2.2 for iterates of the form
![]() $[p_i(n)], 1\leq i\leq k,$
where
$[p_i(n)], 1\leq i\leq k,$
where
![]() $p_i=(p_{i,1},\ldots ,p_{i,d}):\mathbb {Z}^L\to \mathbb {R}^d$
are vectors of real valued polynomials. (Here, for
$p_i=(p_{i,1},\ldots ,p_{i,d}):\mathbb {Z}^L\to \mathbb {R}^d$
are vectors of real valued polynomials. (Here, for
![]() $x=(x_1,\ldots ,x_L)\in \mathbb {R}^L,$
we write
$x=(x_1,\ldots ,x_L)\in \mathbb {R}^L,$
we write ![]() where
where
![]() $[\cdot ]$
is the floor function. In fact, one can consider any combination of rounding functions, that is, floor, ceiling, or closest integer.)
$[\cdot ]$
is the floor function. In fact, one can consider any combination of rounding functions, that is, floor, ceiling, or closest integer.)
7.1 The two-term case with no ergodicity assumptions
Given the results in the [Reference Chu, Frantzikinakis and Host6, Appendix], we are able to obtain the following splitting result for two commuting transformations without any ergodicity assumptions.
Theorem 7.1. Let
![]() $(X,\mathcal {B},\mu ,T,S)$
be a measure-preserving system with
$(X,\mathcal {B},\mu ,T,S)$
be a measure-preserving system with
![]() $TS=ST$
. Let
$TS=ST$
. Let
![]() $f_0,f_1,f_2 \in L^{\infty }(\mu )$
and
$f_0,f_1,f_2 \in L^{\infty }(\mu )$
and
![]() $p \in {\mathbb Z}[n]$
with degree
$p \in {\mathbb Z}[n]$
with degree
![]() $K\geq 2$
. Then, the multicorrelation sequence
$K\geq 2$
. Then, the multicorrelation sequence
can be decomposed as a sum of a uniform limit of K-step nilsequences plus a nullsequence.
Proof. Setting
![]() $F_i=f_i \otimes \bar {f}_i, i=0,1,2,$
and
$F_i=f_i \otimes \bar {f}_i, i=0,1,2,$
and
![]() $\tilde {\mu }=\mu \times \mu ,$
we have that
$\tilde {\mu }=\mu \times \mu ,$
we have that
 $$ \begin{align} \frac{1}{N}\sum_{n=1}^N |a(n)|^2=\frac{1}{N}\sum_{n=1}^N \int_{X^2} F_0\cdot (T \times T)^n F_1\cdot (S \times S)^{p(n)} F_2 \, d\tilde{\mu}. \end{align} $$
$$ \begin{align} \frac{1}{N}\sum_{n=1}^N |a(n)|^2=\frac{1}{N}\sum_{n=1}^N \int_{X^2} F_0\cdot (T \times T)^n F_1\cdot (S \times S)^{p(n)} F_2 \, d\tilde{\mu}. \end{align} $$
Using [Reference Chu, Frantzikinakis and Host6, Theorem A.3], we get that the rational Kronecker factor is characteristic for the averages appearing in equation (43). (The rational Kronecker factor is the smallest sub-
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $\mathcal {B}$
that makes all functions with finite orbit in
$\mathcal {B}$
that makes all functions with finite orbit in
![]() $L^2(\mu )$
under the transformation T measurable.) Consequently, we may replace
$L^2(\mu )$
under the transformation T measurable.) Consequently, we may replace
![]() $f_1$
by
$f_1$
by
![]() $P_cf_1$
and
$P_cf_1$
and
![]() $f_2$
by
$f_2$
by
![]() $Q_cf_2$
in
$Q_cf_2$
in
![]() $a(n)$
up to a nullsequence, where
$a(n)$
up to a nullsequence, where
![]() $P_c$
denotes the orthogonal projection onto the compact component of the splitting associated to T, and
$P_c$
denotes the orthogonal projection onto the compact component of the splitting associated to T, and
![]() $Q_c$
that associated to S. (Here we make use of the Hilbert space splitting of
$Q_c$
that associated to S. (Here we make use of the Hilbert space splitting of
![]() $L^2(\mu )$
into its compact and weakly mixing components for a given unitary operator. The seeds for these results are already present in the work of Koopman and von Neumann [Reference Koopman and von Neumann23]. These were later generalized by Jacobs, Glicksberg, and de Leeuw. See [Reference Eisner, Farkas, Haase and Nagel8, §16.3] for a more modern treatment.) Thus, the sequence
$L^2(\mu )$
into its compact and weakly mixing components for a given unitary operator. The seeds for these results are already present in the work of Koopman and von Neumann [Reference Koopman and von Neumann23]. These were later generalized by Jacobs, Glicksberg, and de Leeuw. See [Reference Eisner, Farkas, Haase and Nagel8, §16.3] for a more modern treatment.) Thus, the sequence
is a nullsequence. Let
![]() $\varepsilon>0$
and choose
$\varepsilon>0$
and choose
![]() $h_1,\ldots ,h_k,g_1,\ldots ,g_k \in L^2(\mu )$
such that
$h_1,\ldots ,h_k,g_1,\ldots ,g_k \in L^2(\mu )$
such that
![]() $Th_i=\lambda _ih_i$
and
$Th_i=\lambda _ih_i$
and
![]() $Sg_i=\rho _ig_i$
(for some
$Sg_i=\rho _ig_i$
(for some
![]() $\lambda _1,\ldots ,\lambda _k,\rho _1,\ldots ,\rho _k \in {\mathbb C}$
of absolute value 1) as well as
$\lambda _1,\ldots ,\lambda _k,\rho _1,\ldots ,\rho _k \in {\mathbb C}$
of absolute value 1) as well as
![]() $a_1,\ldots ,a_k,b_1,\ldots ,b_k \in {\mathbb C}$
such that
$a_1,\ldots ,a_k,b_1,\ldots ,b_k \in {\mathbb C}$
such that
 $$ \begin{align*} \bigg|\int_X f_0 \cdot T^n P_cf_1 \cdot S^{p(n)} Q_c f_2 \, d\mu-\int_X f_0 \cdot T^n \sum_{i=1}^k a_ih_i \cdot S^{p(n)} \sum_{j=1}^k b_jg_j \, d\mu\bigg|<\varepsilon.\end{align*} $$
$$ \begin{align*} \bigg|\int_X f_0 \cdot T^n P_cf_1 \cdot S^{p(n)} Q_c f_2 \, d\mu-\int_X f_0 \cdot T^n \sum_{i=1}^k a_ih_i \cdot S^{p(n)} \sum_{j=1}^k b_jg_j \, d\mu\bigg|<\varepsilon.\end{align*} $$
Observe that
 $$ \begin{align*} \int_X f_0 \cdot T^n \sum_{i=1}^k a_ih_i \cdot S^{p(n)} \sum_{j=1}^k b_ig_i \, d\mu & = \int_X f_0 \cdot \sum_{i=1}^k a_i\lambda_i^nh_i \cdot \sum_{j=1}^k b_j\rho_j^{p(n)}g_j \, d\mu \\ & = \sum_{i,j=1}^k \bigg(a_ib_j \int_X f_0 \cdot h_i \cdot g_j \, d\mu \bigg)\lambda_i^n\rho_j^{p(n)},\end{align*} $$
$$ \begin{align*} \int_X f_0 \cdot T^n \sum_{i=1}^k a_ih_i \cdot S^{p(n)} \sum_{j=1}^k b_ig_i \, d\mu & = \int_X f_0 \cdot \sum_{i=1}^k a_i\lambda_i^nh_i \cdot \sum_{j=1}^k b_j\rho_j^{p(n)}g_j \, d\mu \\ & = \sum_{i,j=1}^k \bigg(a_ib_j \int_X f_0 \cdot h_i \cdot g_j \, d\mu \bigg)\lambda_i^n\rho_j^{p(n)},\end{align*} $$
which is a K-step nilsequence. Applying the same argument as in the proof Theorem 2.2, we deduce the decomposition result. The rest of the details are omitted for the sake of brevity.
It is natural to ask whether a result analogous to Theorem 7.1 holds for longer expressions (potentially via a generalization of the results in the [Reference Chu, Frantzikinakis and Host6, Appendix]), and with more general polynomial iterates, even without necessarily assuming they have distinct degrees. Thus, we state the following problem.
Problem 1. Obtain decomposition results of the form ‘uniform limit of nilsequences plus a nullsequence’ for multicorrelation sequences with (integer) polynomial iterates for general systems under no ergodicity assumptions on the transformations.
7.2 Integer part polynomial iterates
With a, by now, standard argument (introduced in [Reference Boshernitzan, Jones, Wierdl, Bergelson, March and Rosenblatt5, Reference Lesigne30] for a single term, extended for two terms in [Reference Wierdl35], and further developed in [Reference Koutsogiannis24, Reference Koutsogiannis25, Reference Koutsogiannis, Le, Moreira and Richter27]), one has, for the vectors of real polynomials
![]() $p_{i}=(p_{i,1},\ldots ,p_{i,d}),$
that the expression
$p_{i}=(p_{i,1},\ldots ,p_{i,d}),$
that the expression
 $$ \begin{align} \frac{1}{|I_N|}\sum_{n\in I_N}\prod_{i=1}^k T_{[p_i(n)]}f_i=\frac{1}{|I_N|}\sum_{n\in I_N}\prod_{i=1}^k \prod_{j=1}^d T_j^{[p_{i,j}(n)]}f_i \end{align} $$
$$ \begin{align} \frac{1}{|I_N|}\sum_{n\in I_N}\prod_{i=1}^k T_{[p_i(n)]}f_i=\frac{1}{|I_N|}\sum_{n\in I_N}\prod_{i=1}^k \prod_{j=1}^d T_j^{[p_{i,j}(n)]}f_i \end{align} $$
is close to
 $$ \begin{align} \frac{1}{|I_N|}\sum_{n\in I_N}\prod_{i=1}^k \prod_{j=1}^d S_j^{p_{i,j}(n)}g_i, \end{align} $$
$$ \begin{align} \frac{1}{|I_N|}\sum_{n\in I_N}\prod_{i=1}^k \prod_{j=1}^d S_j^{p_{i,j}(n)}g_i, \end{align} $$
where
![]() $S_j$
terms are
$S_j$
terms are
![]() $\mathbb {R}$
-flows on an ‘extension system’ Y of X, and the functions
$\mathbb {R}$
-flows on an ‘extension system’ Y of X, and the functions
![]() $g_i$
are extensions of the
$g_i$
are extensions of the
![]() $f_i$
. (We say that a jointly measurable family
$f_i$
. (We say that a jointly measurable family
![]() $(S_t)_{t\in {\mathbb R}^d}$
of measure-preserving transformations on a probability space is an
$(S_t)_{t\in {\mathbb R}^d}$
of measure-preserving transformations on a probability space is an
![]() ${\mathbb R}^d$
-action (flow), if it satisfies
${\mathbb R}^d$
-action (flow), if it satisfies
![]() $S_{t+r}=S_t\circ S_r$
for all
$S_{t+r}=S_t\circ S_r$
for all
![]() $t,r\in {\mathbb R}^d$
—see [Reference Koutsogiannis25] for details.) As an application of Theorem 2.2, one can prove splitting theorems for
$t,r\in {\mathbb R}^d$
—see [Reference Koutsogiannis25] for details.) As an application of Theorem 2.2, one can prove splitting theorems for
![]() ${\mathbb R}^d$
-actions on the extension system.
${\mathbb R}^d$
-actions on the extension system.
Indeed, consider the multicorrelation sequence
where S is a measure-preserving
![]() ${\mathbb R}^d$
-action on the probability space
${\mathbb R}^d$
-action on the probability space
![]() $(X,\mathcal {B},\mu ), f_0,f_1,\ldots , f_k\in L^\infty (X),$
and
$(X,\mathcal {B},\mu ), f_0,f_1,\ldots , f_k\in L^\infty (X),$
and
![]() $p_{1},\ldots ,p_{k}\colon \mathbb {Z}\to \mathbb {R}^{d}$
a non-degenerate family of polynomials of degree at most K with
$p_{1},\ldots ,p_{k}\colon \mathbb {Z}\to \mathbb {R}^{d}$
a non-degenerate family of polynomials of degree at most K with
![]() $p_{i}(n) = \sum _{h = 0}^K a_{i,h} n^h$
,
$p_{i}(n) = \sum _{h = 0}^K a_{i,h} n^h$
,
![]() $a_{i,h}\in \mathbb {R}^{d}$
. (We address the
$a_{i,h}\in \mathbb {R}^{d}$
. (We address the
![]() $L=1$
case for simplicity; following the same argument, one can similarly get the corresponding result for the general case of L-variable polynomials by using an ordering on the parameters, e.g.
$L=1$
case for simplicity; following the same argument, one can similarly get the corresponding result for the general case of L-variable polynomials by using an ordering on the parameters, e.g.
![]() $n_1>\ldots >n_L.$
) Then
$n_1>\ldots >n_L.$
) Then
 $$ \begin{align*}S_{p_{i}(n)}=S_{\sum_{h = 0}^K a_{i,h} n^h}=\prod_{h=0}^{K}(S_{a_{i,h}})^{n^{h}}.\end{align*} $$
$$ \begin{align*}S_{p_{i}(n)}=S_{\sum_{h = 0}^K a_{i,h} n^h}=\prod_{h=0}^{K}(S_{a_{i,h}})^{n^{h}}.\end{align*} $$
Note that
![]() $S_{a_{i,h}}, 1\leq i\leq k, 1\leq h\leq K$
generate a
$S_{a_{i,h}}, 1\leq i\leq k, 1\leq h\leq K$
generate a
![]() ${\mathbb Z}^{kK}$
-action on
${\mathbb Z}^{kK}$
-action on
![]() $(X,\mathcal {B},\mu )$
. For convenience, set
$(X,\mathcal {B},\mu )$
. For convenience, set
![]() $p_{0}$
to be the constant zero polynomial. For
$p_{0}$
to be the constant zero polynomial. For
![]() $0\leq i, j\leq k, i\neq j$
, let
$0\leq i, j\leq k, i\neq j$
, let
![]() $D_{i,j}$
be the largest integer h so that
$D_{i,j}$
be the largest integer h so that
![]() $S_{a_{i,D_{i,j}}-a_{j,D_{i,j}}}\neq \textrm {id}$
. This transformation will be denoted by
$S_{a_{i,D_{i,j}}-a_{j,D_{i,j}}}\neq \textrm {id}$
. This transformation will be denoted by
![]() $R_{i,j}$
. By Theorem 2.2, one can show the desired splitting result for the sequence in equation (46), if the transformations
$R_{i,j}$
. By Theorem 2.2, one can show the desired splitting result for the sequence in equation (46), if the transformations
![]() $R_{i,j}, 0\leq i, j\leq k, i\neq j$
are all ergodic (as
$R_{i,j}, 0\leq i, j\leq k, i\neq j$
are all ergodic (as
![]() ${\mathbb Z}$
-actions on the extension system Y).
${\mathbb Z}$
-actions on the extension system Y).
Unfortunately, even though we have the previous result for flows, the error term that arises from the approximation of equation (44) by equation (45) prevents us from getting the conclusion of Theorem 2.2 for multicorrelation sequences of the form
(To this day, only splittings of the form nilsequence plus an error term that is small in uniform density are known for this class of multicorrelation sequences (for this, see [Reference Koutsogiannis25]). One is referred to [Reference Koutsogiannis, Le, Moreira and Richter27] for averages along primes for the error term—in this last reference, only single variable real polynomials were considered. Using the multivariable approach of [Reference Frantzikinakis, Host and Kra12] instead of [Reference Frantzikinakis and Host10], one immediately gets the aforementioned result for integer part, or indeed for combinations of any other rounding functions, multivariable real polynomial iterates.)
Remark 7.2. It is important to stress that, for integer part real polynomial iterates, one does not expect to have the desired multicorrelation splitting in general. The next example shows that, even for
![]() $k=1,$
an ergodic system, and linear iterates, it can be too much to hope for.
$k=1,$
an ergodic system, and linear iterates, it can be too much to hope for.
Example 7.3. Following [Reference Koutsogiannis, Le, Moreira and Richter27, Example 7], let ![]() ,
,
![]() $T(x)=x+1/\sqrt {2}$
,
$T(x)=x+1/\sqrt {2}$
,
![]() $p(n)=\sqrt {2}n$
,
$p(n)=\sqrt {2}n$
,
![]() $f_0(x)=e(x)$
and
$f_0(x)=e(x)$
and
![]() $f_1(x)=e(-x)$
, where
$f_1(x)=e(-x)$
, where ![]() . Then, we have that
. Then, we have that
 $$ \begin{align*} \int_X f_0\cdot T^{[p(n)]}f_1\, d\mu = \int_X e(x) e\bigg(-x-\frac{1}{\sqrt{2}} [\sqrt{2}n]\bigg)\,dx = e \bigg( - \frac{1}{\sqrt{2}} [\sqrt{2} n] \bigg) = e\bigg(\frac{1}{\sqrt{2}}\{\sqrt{2}n\}\bigg), \end{align*} $$
$$ \begin{align*} \int_X f_0\cdot T^{[p(n)]}f_1\, d\mu = \int_X e(x) e\bigg(-x-\frac{1}{\sqrt{2}} [\sqrt{2}n]\bigg)\,dx = e \bigg( - \frac{1}{\sqrt{2}} [\sqrt{2} n] \bigg) = e\bigg(\frac{1}{\sqrt{2}}\{\sqrt{2}n\}\bigg), \end{align*} $$
which cannot be written as a uniform limit of nilsequences and a nullsequence.
Remark 7.4. One may think that the fact that
![]() $\sqrt {2}$
and
$\sqrt {2}$
and
![]() ${1}/{\sqrt {2}}$
are not linearly independent over
${1}/{\sqrt {2}}$
are not linearly independent over
![]() ${\mathbb Q}$
is behind the impossibility of the splitting in the example above. However, a closer examination of the proof given in [Reference Koutsogiannis, Le, Moreira and Richter27] shows that this is not the case, and that the failure extends quite generally.
${\mathbb Q}$
is behind the impossibility of the splitting in the example above. However, a closer examination of the proof given in [Reference Koutsogiannis, Le, Moreira and Richter27] shows that this is not the case, and that the failure extends quite generally.
Indeed, we can imitate the example quoted above as follows. Let
![]() $(X,\mathcal {B},\mu ,T)$
be an ergodic measure-preserving system with non-trivial irrational spectrum. Let
$(X,\mathcal {B},\mu ,T)$
be an ergodic measure-preserving system with non-trivial irrational spectrum. Let
![]() $f_1 : X \to \mathbb {S}^1$
be an eigenfunction of T with eigenvalue
$f_1 : X \to \mathbb {S}^1$
be an eigenfunction of T with eigenvalue
![]() $e^{2\pi i \beta }$
, with
$e^{2\pi i \beta }$
, with
![]() $\beta \in {\mathbb R} \setminus {\mathbb Q}$
. Put
$\beta \in {\mathbb R} \setminus {\mathbb Q}$
. Put
![]() $f_0=\bar {f_1}$
. Then, if we consider the multicorrelation sequence
$f_0=\bar {f_1}$
. Then, if we consider the multicorrelation sequence
with the choices made above, we observe that, in fact,
![]() $a(n)=e^{2\pi i [\alpha n]\beta }.$
The same argument as in [Reference Koutsogiannis, Le, Moreira and Richter27, Example 7] shows that
$a(n)=e^{2\pi i [\alpha n]\beta }.$
The same argument as in [Reference Koutsogiannis, Le, Moreira and Richter27, Example 7] shows that
![]() $a(n)$
cannot be written as a uniform limit of nilsequences plus a nullsequence.
$a(n)$
cannot be written as a uniform limit of nilsequences plus a nullsequence.
However, if we postulate very strong assumptions on our transformations, we do have the desired decomposition results. For example (see [Reference Koutsogiannis25]), if
![]() $T_1,\ldots ,T_k$
are commuting weakly mixing transformations on
$T_1,\ldots ,T_k$
are commuting weakly mixing transformations on
![]() $(X,\mathcal {B},\mu )$
,
$(X,\mathcal {B},\mu )$
,
![]() $q_i(n)=p_i(n)e_i, 1\leq i\leq k,$
where
$q_i(n)=p_i(n)e_i, 1\leq i\leq k,$
where
![]() $p_i\colon \mathbb {Z}\to \mathbb {R}$
are real polynomials of distinct, positive degrees, and
$p_i\colon \mathbb {Z}\to \mathbb {R}$
are real polynomials of distinct, positive degrees, and
![]() $f_1,\ldots ,f_k \in L^{\infty }(\mu ),$
then we have that
$f_1,\ldots ,f_k \in L^{\infty }(\mu ),$
then we have that
 $$ \begin{align*} \lim_{N-M \to \infty} \frac{1}{N-M}\sum_{n=M}^{N-1}T_{[q_1(n)]}f_1 \cdots T_{[q_k(n)]}f_k=\prod_{i=1}^k \int_X f_i \, d\mu.\end{align*} $$
$$ \begin{align*} \lim_{N-M \to \infty} \frac{1}{N-M}\sum_{n=M}^{N-1}T_{[q_1(n)]}f_1 \cdots T_{[q_k(n)]}f_k=\prod_{i=1}^k \int_X f_i \, d\mu.\end{align*} $$
Hence, for any
![]() $f_0 \in L^{\infty }(\mu ),$
the multicorrelation sequence
$f_0 \in L^{\infty }(\mu ),$
the multicorrelation sequence
can be written as a sum of a constant (that is, a
![]() $0$
-step nilsequence) and a nullsequence.
$0$
-step nilsequence) and a nullsequence.
We conclude this article with the following problem that arises naturally.
Problem 2. Let
![]() $d,k,K,L\in \mathbb {N}, p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {R}^{d}$
be a non-degenerate family of polynomials of degree at most K,
$d,k,K,L\in \mathbb {N}, p_{1},\ldots ,p_{k}\colon \mathbb {Z}^{L}\to \mathbb {R}^{d}$
be a non-degenerate family of polynomials of degree at most K,
![]() $(X,\mathcal {B},\mu ,T_1,\ldots ,T_d)$
a measure-preserving system, and
$(X,\mathcal {B},\mu ,T_1,\ldots ,T_d)$
a measure-preserving system, and
![]() $f_0,\ldots ,f_k \in L^{\infty }(\mu ).$
Find conditions, on the
$f_0,\ldots ,f_k \in L^{\infty }(\mu ).$
Find conditions, on the
![]() $p_i$
and/or the
$p_i$
and/or the
![]() $\mathbb {Z}^d$
-action T that is defined by the
$\mathbb {Z}^d$
-action T that is defined by the
![]() $T_i$
, so that the multicorrelation sequence
$T_i$
, so that the multicorrelation sequence
can be decomposed as a sum of a uniform limit of D-step nilsequences and a nullsequence.
Acknowledgements
We would like to thank Nikos Frantzikinakis for a number of helpful comments and corrections, and the anonymous referee for a detailed and very helpful report, which greatly improved the presentation of the article. S.D. was supported by ANID/Fondecyt/1200897 and Centro de Modelamiento Matemático (CMM), FB210005, BASAL funds for centers of excellence from ANID-Chile.