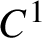1 Introduction
One of the strongest characteristics of chaotic behaviour in dynamical systems is the exponential decay of correlations, or exponential mixing; in addition to being of intrinsic interest, this is typically accompanied by other strong statistical properties for regular observables. Naturally, there has been substantial interest in understanding and characterizing the dynamical systems with this property.
Hyperbolicity and the joint structure of the strong stable and strong unstable foliations are among the most well-understood mechanisms driving chaotic behaviour in both discrete-time and continuous-time dynamical systems. For continuous-time systems in particular, the extent to which these foliations fail to be integrable is known to be especially important.
Unfortunately, even among Anosov flows, there is no complete characterization of those which are exponentially mixing. There have been many significant advances, however, and we note only a few results that are relevant to our main result: we refer the reader to [Reference Butterley and War9, §1] for an excellent narrative.
Perhaps the most notable result was due to Dolgopyat, who showed in [Reference Dolgopyat11] that smooth Anosov flows with
![]() $C^1$
stable and unstable foliations were exponentially mixing, via a quantitative non-integrability estimate. Recently, [Reference Butterley and War9]—following related work by [Reference Araújo and Melbourne3–Reference Baladi and Vallée5]—established exponential mixing for Anosov flows in the absence of any regularity hypotheses on the unstable foliation.
$C^1$
stable and unstable foliations were exponentially mixing, via a quantitative non-integrability estimate. Recently, [Reference Butterley and War9]—following related work by [Reference Araújo and Melbourne3–Reference Baladi and Vallée5]—established exponential mixing for Anosov flows in the absence of any regularity hypotheses on the unstable foliation.
Our attention will be restricted to the class of Anosov flows studied in [Reference Butterley and War9, Reference Dolgopyat11], which are known to be exponentially mixing. We consider compact isometric extensions of these flows, and give criteria for these extensions to be exponentially mixing. We prove the following result.
Theorem A. Let M, N and F be closed Riemannian manifolds, where
![]() $\pi \colon M \to N$
is a fibre bundle with fibres isometric to F. Suppose that
$\pi \colon M \to N$
is a fibre bundle with fibres isometric to F. Suppose that
![]() $g_t \colon N \to N$
is a
$g_t \colon N \to N$
is a
![]() $C^{2+\epsilon }$
transitive Anosov flow preserving an equilibrium measure
$C^{2+\epsilon }$
transitive Anosov flow preserving an equilibrium measure
![]() $\nu $
with a Hölder potential
$\nu $
with a Hölder potential
![]() $\varsigma \colon N \to \mathbb {R}$
. Moreover, suppose that either:
$\varsigma \colon N \to \mathbb {R}$
. Moreover, suppose that either:
-
(i) the strong stable and strong unstable foliations are
 $C^1$
, and
$C^1$
, and
 $\nu $
has unstable conditional measures
$\nu $
has unstable conditional measures
 $\nu ^u$
that are diametrically regular; or
$\nu ^u$
that are diametrically regular; or -
(ii) the strong stable foliation is
 $C^{1+\epsilon '}$
for some
$C^{1+\epsilon '}$
for some
 $\epsilon '> 0$
, and
$\epsilon '> 0$
, and
 $\nu $
is the
$\nu $
is the
 $g_t$
-invariant Riemannian volume.
$g_t$
-invariant Riemannian volume.
Let G be a closed, connected, normal subgroup of the isometry group
![]() $\operatorname {\mathrm {Isom}}(F)$
that acts transitively on F, and equip F with the pushforward
$\operatorname {\mathrm {Isom}}(F)$
that acts transitively on F, and equip F with the pushforward
![]() $\omega $
of the normalized Haar measure on G. Let
$\omega $
of the normalized Haar measure on G. Let
![]() $f_t \colon M \to M$
be a G-extension of
$f_t \colon M \to M$
be a G-extension of
![]() $g_t$
. If
$g_t$
. If
![]() $f_t$
is locally G-accessible, then it enjoys exponential decay of correlations of all orders for the invariant product measure
$f_t$
is locally G-accessible, then it enjoys exponential decay of correlations of all orders for the invariant product measure
![]() $\nu \times \omega $
. (Here, the product measure
$\nu \times \omega $
. (Here, the product measure
![]() $\nu \times \omega $
refers to the pushforward of the locally defined measure
$\nu \times \omega $
refers to the pushforward of the locally defined measure
![]() $\nu \times \omega $
on trivialization charts, where the fibrewise measures are obviously compatible so long as the trivializations are G-equivariant.)
$\nu \times \omega $
on trivialization charts, where the fibrewise measures are obviously compatible so long as the trivializations are G-equivariant.)
In fact, the main portion of our argument, obtaining quantitative non-integrability estimates for the extension in terms of the infinitesimal transitivity group described in Definition 4.3, only requires that the strong stable distribution is
![]() $C^1$
. The additional regularity hypotheses are merely required to obtain the necessary spectral bounds for the symbolic transfer operator associated to the dynamical system on the base manifold. In particular, (i) would allow us to invoke [Reference Dolgopyat11, Theorem 2], whereas (ii) would allow us to instead invoke [Reference Butterley and War9, Proposition 3.16].
$C^1$
. The additional regularity hypotheses are merely required to obtain the necessary spectral bounds for the symbolic transfer operator associated to the dynamical system on the base manifold. In particular, (i) would allow us to invoke [Reference Dolgopyat11, Theorem 2], whereas (ii) would allow us to instead invoke [Reference Butterley and War9, Proposition 3.16].
Note that qualitative mixing in this context can be deduced quickly from very broad theorems for partially hyperbolic systems; specifically, we note the general result of Burns and Wilkinson in [Reference Burns and Wilkinson8] that essentially accessible centre-bunched volume-preserving systems are mixing of all orders. Quantitative results, on the other hand, seem to require a more specialized approach.
Theorem A is analogous to a result of Dolgopyat, who showed in [Reference Dolgopyat12] that accessible compact group extensions of discrete-time expanding dynamical systems are exponentially mixing, and whose techniques we make heavy use of in our proof. Our approach follows the strategy Winter used in [Reference Sharp17] to establish exponential mixing for frame flows over convex cocompact hyperbolic manifolds with Dolgopyat’s techniques. We begin by constructing a symbolic model for the extension flow, establishing uniform local non-integrability estimates for this symbolic model and using arguments employed by Dolgopyat in both [Reference Dolgopyat11, Reference Dolgopyat12] to obtain bounds for the spectrum of certain ‘twisted’ transfer operators. Our main technical result is the following bound.
Theorem B. Fix notation as in Theorem A, and suppose that the potential
![]() $\varsigma $
is
$\varsigma $
is
![]() $C^1$
. Then there are constants
$C^1$
. Then there are constants
![]() $C> 0$
and
$C> 0$
and
![]() $r < 1$
so that we have
$r < 1$
so that we have
for all
![]() $\varphi \in C^1(U, V^\rho )$
, all non-trivial irreducible representations
$\varphi \in C^1(U, V^\rho )$
, all non-trivial irreducible representations
![]() $\rho $
of G, and any
$\rho $
of G, and any
![]() $z \in \mathbb {C}$
with
$z \in \mathbb {C}$
with
![]() $|\mathrm {Re}(z) - P(\varsigma )| < 1$
.
$|\mathrm {Re}(z) - P(\varsigma )| < 1$
.
The principal novelty here, and our main point of divergence with [Reference Sharp17], is that we use the local G-accessibility (see Definition 2.4) of the extension flow
![]() $f_t$
to obtain the necessary local non-integrability estimates. As in [Reference Sharp17], we measure the local non-integrability of the extension using Dolgopyat’s infinitesimal transitivity group.
$f_t$
to obtain the necessary local non-integrability estimates. As in [Reference Sharp17], we measure the local non-integrability of the extension using Dolgopyat’s infinitesimal transitivity group.
Although we rely heavily on the techniques used in [Reference Dolgopyat12], translating these into our setting presents several difficulties. Most notably, the non-integrability of the strong stable and unstable foliations of the base flow
![]() $g_t$
and the non-triviality of the fibre bundle
$g_t$
and the non-triviality of the fibre bundle
![]() $\pi \colon M \to N$
require some additional care to properly deal with, though we are ultimately able to adapt many of the same arguments.
$\pi \colon M \to N$
require some additional care to properly deal with, though we are ultimately able to adapt many of the same arguments.
One of the most striking applications of quantitative mixing results in this setting has been the recent work of Kahn and Markovic, using the exponential mixing of frame flows on hyperbolic manifolds in their resolution of the surface subgroup conjecture in [Reference Kahn and Markovic14]. In the specific case of the frame flow, Theorem A can be stated more succinctly.
Corollary C. Let N be the unit tangent bundle of a closed
![]() $C^{2+\epsilon}\ n$
-manifold of quarter-pinched negative curvature equipped with an invariant Riemannian volume
$C^{2+\epsilon}\ n$
-manifold of quarter-pinched negative curvature equipped with an invariant Riemannian volume
![]() $\nu $
, and let M be the oriented full frame bundle over N equipped with the extension
$\nu $
, and let M be the oriented full frame bundle over N equipped with the extension
![]() $\nu \times \omega $
by the Haar measure on
$\nu \times \omega $
by the Haar measure on
![]() $\operatorname {\mathrm {SO}}(n-1)$
. If the frame flow
$\operatorname {\mathrm {SO}}(n-1)$
. If the frame flow
![]() $f_t$
is locally accessible, then it enjoys exponential decay of correlations of all orders.
$f_t$
is locally accessible, then it enjoys exponential decay of correlations of all orders.
2 Preliminaries
We fix some notation that we use throughout this paper: N will be a closed Riemannian manifold equipped with a probability measure
![]() $\nu $
and
$\nu $
and
![]() $g_t \colon N \to N$
a
$g_t \colon N \to N$
a
![]() $C^\infty $
Anosov flow preserving
$C^\infty $
Anosov flow preserving
![]() $\nu $
. Let M be a compact Riemannian fibre bundle
$\nu $
. Let M be a compact Riemannian fibre bundle
![]() $\pi \colon M \to N$
whose fibres
$\pi \colon M \to N$
whose fibres
![]() $\pi ^{-1}(x)$
are each isometric to a fixed compact, Riemannian manifold F, and let
$\pi ^{-1}(x)$
are each isometric to a fixed compact, Riemannian manifold F, and let
![]() $f_t \colon M \to M$
be an extension of
$f_t \colon M \to M$
be an extension of
![]() $g_t$
satisfying
$g_t$
satisfying
![]() $\pi \circ f_t = g_t \circ \pi $
. We equip M with the product measure
$\pi \circ f_t = g_t \circ \pi $
. We equip M with the product measure
![]() $\mu $
of
$\mu $
of
![]() $\nu $
and a probability measure on F.
$\nu $
and a probability measure on F.
The motivating example for everything that follows is when N is the unit tangent bundle for a closed n-manifold of quarter-pinched negative curvature, M is the oriented orthonormal frame bundle,
![]() $g_t$
is the geodesic flow and
$g_t$
is the geodesic flow and
![]() $f_t$
is the frame flow. In this case, we take
$f_t$
is the frame flow. In this case, we take
![]() $\nu $
to be the Liouville measure on N, and
$\nu $
to be the Liouville measure on N, and
![]() $\mu $
to be the local product of the Liouville measure and the normalized Haar measure on
$\mu $
to be the local product of the Liouville measure and the normalized Haar measure on
![]() $\operatorname {\mathrm {SO}}(n-1,\mathbb {R})$
.
$\operatorname {\mathrm {SO}}(n-1,\mathbb {R})$
.
2.1 Dynamical preliminaries
Our goal is to show that, with appropriate hypotheses,
![]() $f_t$
enjoys exponential decay of correlations or, equivalently, is exponentially mixing.
$f_t$
enjoys exponential decay of correlations or, equivalently, is exponentially mixing.
Definition 2.1. A flow
![]() $f_t$
is said to be exponentially mixing of order k for
$f_t$
is said to be exponentially mixing of order k for
![]() $C^\alpha $
functions if there are constants
$C^\alpha $
functions if there are constants
![]() $C> 0$
and
$C> 0$
and
![]() $r < 1$
so that
$r < 1$
so that

for all
![]() $\varphi _i \in C^\alpha (M, \mathbb {C})$
. Here,
$\varphi _i \in C^\alpha (M, \mathbb {C})$
. Here,
![]() $\| \cdot \|_{C^\alpha }$
denotes the usual
$\| \cdot \|_{C^\alpha }$
denotes the usual
![]() $\alpha $
-Hölder norm
$\alpha $
-Hölder norm

on the space
![]() $C^\alpha (M, \mathbb {C})$
of
$C^\alpha (M, \mathbb {C})$
of
![]() $\alpha $
-Hölder complex-valued functions.
$\alpha $
-Hölder complex-valued functions.
Actually, we prove that there are constants
![]() $C> 0$
and
$C> 0$
and
![]() $r < $
so that
$r < $
so that
 $$ \begin{align*} \bigg| \int_M \varphi_0 \cdot ( \varphi_1 \circ f_{t_1} ) \cdot \cdots \cdot ( \varphi_k \circ f_{t_k} ) \, d\nu \bigg| < C r^{\max t_i} \cdot \|\varphi_0\|_{C^\alpha} \cdot \cdots \cdot \|\varphi_k\|_{C^\alpha} \end{align*} $$
$$ \begin{align*} \bigg| \int_M \varphi_0 \cdot ( \varphi_1 \circ f_{t_1} ) \cdot \cdots \cdot ( \varphi_k \circ f_{t_k} ) \, d\nu \bigg| < C r^{\max t_i} \cdot \|\varphi_0\|_{C^\alpha} \cdot \cdots \cdot \|\varphi_k\|_{C^\alpha} \end{align*} $$
for all
![]() $\varphi _i \in C^\alpha (M, \mathbb {C})$
with
$\varphi _i \in C^\alpha (M, \mathbb {C})$
with
![]() $\int _M \varphi _i \, d\nu = 0$
. It is an elementary exercise to show that this is equivalent to Definition 2.1.
$\int _M \varphi _i \, d\nu = 0$
. It is an elementary exercise to show that this is equivalent to Definition 2.1.
Although having some degree of regularity is critical, exponential mixing for Hölder functions and exponential mixing for more regular functions are typically equivalent by a standard approximation argument. We provide a brief outline of the proof here.
Lemma 2.1. Suppose
![]() $f_t$
is exponentially mixing of order k for
$f_t$
is exponentially mixing of order k for
![]() $C^1$
functions. Then,
$C^1$
functions. Then,
![]() $f_t$
is exponentially mixing of order k for
$f_t$
is exponentially mixing of order k for
![]() $C^\alpha $
functions, for any
$C^\alpha $
functions, for any
![]() $\alpha> 0$
.
$\alpha> 0$
.
Proof. We perform the argument in the case
![]() $k = 1$
. The general case can be obtained by repeating this inductively.
$k = 1$
. The general case can be obtained by repeating this inductively.
It is well known that, given
![]() $\varphi \in C^\alpha (M, \mathbb {C})$
, we can find smooth approximations
$\varphi \in C^\alpha (M, \mathbb {C})$
, we can find smooth approximations
![]() $\varphi _\epsilon $
to
$\varphi _\epsilon $
to
![]() $\varphi $
with
$\varphi $
with
![]() $\int _M \varphi _\epsilon \, d\mu = 0$
satisfying
$\int _M \varphi _\epsilon \, d\mu = 0$
satisfying
 $$ \begin{align*} \|\varphi_\epsilon - \varphi\|_{C^0} \leq \epsilon^\alpha \|\varphi\|_{C^\alpha}\quad \text{and}\quad \|\varphi_\epsilon\|_{C^1} \leq \epsilon^{-{\dim}(M) - 1} \|\varphi\|_{C^0} \end{align*} $$
$$ \begin{align*} \|\varphi_\epsilon - \varphi\|_{C^0} \leq \epsilon^\alpha \|\varphi\|_{C^\alpha}\quad \text{and}\quad \|\varphi_\epsilon\|_{C^1} \leq \epsilon^{-{\dim}(M) - 1} \|\varphi\|_{C^0} \end{align*} $$
for any
![]() $\epsilon> 0$
; a proof of this can be found, for instance, in [Reference Gorodnik and Spatzier13, Lemma 2.4]. As
$\epsilon> 0$
; a proof of this can be found, for instance, in [Reference Gorodnik and Spatzier13, Lemma 2.4]. As
![]() $f_t$
is exponentially mixing (at rate, say,
$f_t$
is exponentially mixing (at rate, say,
![]() $r^t$
) for
$r^t$
) for
![]() $C^1$
functions by hypothesis, we can write
$C^1$
functions by hypothesis, we can write
 $$ \begin{align*} &\bigg| \int_M \varphi \cdot (\psi \circ f_t) \, d\mu \bigg|\\ &\quad\leq \bigg| \int_M \varphi \cdot (\psi \circ f_t) \, d\mu - \int_M \varphi_\epsilon \cdot (\psi \circ f_t) \, d\mu \bigg| + \bigg| \int_M \varphi_\epsilon \cdot (\psi \circ f_t) \, d\mu \bigg|\\ &\quad\leq \bigg| \int_M (\varphi - \varphi_\epsilon) \cdot (\psi \circ f_t) \, d\mu \bigg| + Cr^t \|\varphi_\epsilon\|_{C^1} \|\psi\|_{C^1} \\ &\quad\leq \|\varphi - \varphi_\epsilon\|_{C^0} \|\psi\|_{C^0} + Cr^t \epsilon^{-(\dim(M) + 1)}\|\varphi\|_{C^0} \|\psi\|_{C^1} \\ &\quad\leq \epsilon^\alpha \|\varphi\|_{C^\alpha} \|\psi\|_{C^0} + C r^t\epsilon^{-(\dim(M)+1)}\|\varphi\|_{C^\alpha} \|\psi\|_{C^1} \\ &\quad= ( \epsilon^\alpha + C r^t\epsilon^{-(\dim(M)+1)} ) \|\varphi\|_{C^\alpha} \|\psi\|_{C^1} \end{align*} $$
$$ \begin{align*} &\bigg| \int_M \varphi \cdot (\psi \circ f_t) \, d\mu \bigg|\\ &\quad\leq \bigg| \int_M \varphi \cdot (\psi \circ f_t) \, d\mu - \int_M \varphi_\epsilon \cdot (\psi \circ f_t) \, d\mu \bigg| + \bigg| \int_M \varphi_\epsilon \cdot (\psi \circ f_t) \, d\mu \bigg|\\ &\quad\leq \bigg| \int_M (\varphi - \varphi_\epsilon) \cdot (\psi \circ f_t) \, d\mu \bigg| + Cr^t \|\varphi_\epsilon\|_{C^1} \|\psi\|_{C^1} \\ &\quad\leq \|\varphi - \varphi_\epsilon\|_{C^0} \|\psi\|_{C^0} + Cr^t \epsilon^{-(\dim(M) + 1)}\|\varphi\|_{C^0} \|\psi\|_{C^1} \\ &\quad\leq \epsilon^\alpha \|\varphi\|_{C^\alpha} \|\psi\|_{C^0} + C r^t\epsilon^{-(\dim(M)+1)}\|\varphi\|_{C^\alpha} \|\psi\|_{C^1} \\ &\quad= ( \epsilon^\alpha + C r^t\epsilon^{-(\dim(M)+1)} ) \|\varphi\|_{C^\alpha} \|\psi\|_{C^1} \end{align*} $$
for any fixed
![]() $t> 0$
. Note that the last line does not involve
$t> 0$
. Note that the last line does not involve
![]() $\varphi _\epsilon $
, so we can simply set
$\varphi _\epsilon $
, so we can simply set
![]() $\epsilon = r^{kt}$
with
$\epsilon = r^{kt}$
with
![]() $k = 1/{2(\dim (M) + 1)}$
. This leaves us with the inequality
$k = 1/{2(\dim (M) + 1)}$
. This leaves us with the inequality
 $$ \begin{align*} \bigg| \int_M \varphi \cdot (\psi \circ f_t) \, d\mu \bigg| &\leq (r^{\alpha(\dim(M) + 1)^{-1} t} + Cr^t r^{-( 1/2)t}) \|\varphi\|_{C^\alpha} \|\psi\|_{C^1}\\ &\leq (1 + C)(r^{\min( 1/ 2, \alpha (\dim(M) + 1)^{-1})})^t \|\varphi\|_{C^\alpha} \|\psi\|_{C^1} \end{align*} $$
$$ \begin{align*} \bigg| \int_M \varphi \cdot (\psi \circ f_t) \, d\mu \bigg| &\leq (r^{\alpha(\dim(M) + 1)^{-1} t} + Cr^t r^{-( 1/2)t}) \|\varphi\|_{C^\alpha} \|\psi\|_{C^1}\\ &\leq (1 + C)(r^{\min( 1/ 2, \alpha (\dim(M) + 1)^{-1})})^t \|\varphi\|_{C^\alpha} \|\psi\|_{C^1} \end{align*} $$
and, noting that the base of the exponential term is at most
![]() $1$
, we see that
$1$
, we see that
![]() $f_t$
is exponentially mixing for any
$f_t$
is exponentially mixing for any
![]() $\varphi \in C^\alpha (M)$
and
$\varphi \in C^\alpha (M)$
and
![]() $\psi \in C^1(M)$
. Now, set
$\psi \in C^1(M)$
. Now, set
![]() $D := C + 1$
and
$D := C + 1$
and
![]() $s := r^{\min (1/2, \alpha (\dim (M) + 1)^{-1})}$
and consider
$s := r^{\min (1/2, \alpha (\dim (M) + 1)^{-1})}$
and consider
![]() $\varphi , \xi \in C^\alpha (M)$
. Once again, we can find a smooth approximation
$\varphi , \xi \in C^\alpha (M)$
. Once again, we can find a smooth approximation
![]() $\xi _\epsilon $
to
$\xi _\epsilon $
to
![]() $\xi $
with
$\xi $
with
![]() $\int _M \xi \, d\mu = 0$
satisfying
$\int _M \xi \, d\mu = 0$
satisfying
 $$ \begin{align*} \|\xi_\epsilon - \xi\|_{C^0} \leq \epsilon^\alpha \|\xi\|_{C^\alpha} \quad\text{and}\quad \|\xi_\epsilon\|_{C^1} \leq \epsilon^{-\dim(M) - 1} \|\xi\|_{C^0} \end{align*} $$
$$ \begin{align*} \|\xi_\epsilon - \xi\|_{C^0} \leq \epsilon^\alpha \|\xi\|_{C^\alpha} \quad\text{and}\quad \|\xi_\epsilon\|_{C^1} \leq \epsilon^{-\dim(M) - 1} \|\xi\|_{C^0} \end{align*} $$
for all
![]() $\epsilon> 0$
. By what we have just shown, we can now write
$\epsilon> 0$
. By what we have just shown, we can now write
 $$ \begin{align*} &\bigg| \int_M \varphi \cdot (\xi \circ f_t) \, d\mu \bigg|\\ &\quad\leq \bigg| \int_M \varphi \cdot (\xi \circ f_t) \, d\mu - \int_M \varphi \cdot (\xi_\epsilon \circ f_t) \, d\mu \bigg| + \bigg| \int_M \varphi \cdot (\xi_\epsilon \circ f_t) \, d\mu \bigg|\\ &\quad\leq \bigg| \int_M \varphi \cdot ( (\xi - \xi_\epsilon) \circ f_t) \, d\mu \bigg| + Ds^t \|\varphi\|_{C^\alpha} \|\xi_\epsilon\|_{C^1}\\ &\quad\leq \|\xi - \xi_\epsilon\|_{C^0} \|\varphi\|_{C^0} + Ds^t \epsilon^{-(\dim(M)+1)} \|\varphi\|_{C^\alpha} \|\xi\|_{C^0}\\ &\quad\leq \epsilon^\alpha\|\xi\|_{C^\alpha} \|\varphi\|_{C^\alpha} + Ds^t \epsilon^{-(\dim(M)+1)} \|\varphi\|_{C^\alpha} \|\xi\|_{C^\alpha}\\ &\quad\leq (\epsilon^\alpha + Ds^t \epsilon^{-(\dim(M)+1)}) \|\varphi\|_{C^\alpha} \|\xi\|_{C^\alpha} \end{align*} $$
$$ \begin{align*} &\bigg| \int_M \varphi \cdot (\xi \circ f_t) \, d\mu \bigg|\\ &\quad\leq \bigg| \int_M \varphi \cdot (\xi \circ f_t) \, d\mu - \int_M \varphi \cdot (\xi_\epsilon \circ f_t) \, d\mu \bigg| + \bigg| \int_M \varphi \cdot (\xi_\epsilon \circ f_t) \, d\mu \bigg|\\ &\quad\leq \bigg| \int_M \varphi \cdot ( (\xi - \xi_\epsilon) \circ f_t) \, d\mu \bigg| + Ds^t \|\varphi\|_{C^\alpha} \|\xi_\epsilon\|_{C^1}\\ &\quad\leq \|\xi - \xi_\epsilon\|_{C^0} \|\varphi\|_{C^0} + Ds^t \epsilon^{-(\dim(M)+1)} \|\varphi\|_{C^\alpha} \|\xi\|_{C^0}\\ &\quad\leq \epsilon^\alpha\|\xi\|_{C^\alpha} \|\varphi\|_{C^\alpha} + Ds^t \epsilon^{-(\dim(M)+1)} \|\varphi\|_{C^\alpha} \|\xi\|_{C^\alpha}\\ &\quad\leq (\epsilon^\alpha + Ds^t \epsilon^{-(\dim(M)+1)}) \|\varphi\|_{C^\alpha} \|\xi\|_{C^\alpha} \end{align*} $$
for any fixed
![]() $t> 0$
. Once again, we can set
$t> 0$
. Once again, we can set
![]() $\epsilon = s^{kt}$
with
$\epsilon = s^{kt}$
with
![]() $k = 1/ {2(\dim (M) + 1)}$
, leaving us with the bound
$k = 1/ {2(\dim (M) + 1)}$
, leaving us with the bound
 $$ \begin{align*} \bigg| \int_M \varphi \cdot (\xi \circ f_t) \, d\mu \bigg| &\leq (s^{\alpha(\dim(M) + 1)^{-1} t} + Ds^t s^{-(1/2)t}) \|\varphi\|_{C^\alpha} \|\xi\|_{C^\alpha}\\ &\leq (1 + D)(s^{\min(1/ 2, \alpha (\dim(M) + 1)^{-1})})^t \|\varphi\|_{C^\alpha} \|\xi\|_{C^\alpha}, \end{align*} $$
$$ \begin{align*} \bigg| \int_M \varphi \cdot (\xi \circ f_t) \, d\mu \bigg| &\leq (s^{\alpha(\dim(M) + 1)^{-1} t} + Ds^t s^{-(1/2)t}) \|\varphi\|_{C^\alpha} \|\xi\|_{C^\alpha}\\ &\leq (1 + D)(s^{\min(1/ 2, \alpha (\dim(M) + 1)^{-1})})^t \|\varphi\|_{C^\alpha} \|\xi\|_{C^\alpha}, \end{align*} $$
which is independent of
![]() $\epsilon $
. Once again, we note that the base of the exponential term is at most one and does not depend on
$\epsilon $
. Once again, we note that the base of the exponential term is at most one and does not depend on
![]() $\varphi $
or
$\varphi $
or
![]() $\xi $
, completing our proof.
$\xi $
, completing our proof.
Henceforth, we restrict our focus to establishing exponential mixing for
![]() $C^1$
functions; exponential mixing for Hölder functions then follows by Lemma 2.1. Of course, whether a system is exponentially mixing depends on the measure under consideration: we are interested in equilibrium measures for Hölder potentials.
$C^1$
functions; exponential mixing for Hölder functions then follows by Lemma 2.1. Of course, whether a system is exponentially mixing depends on the measure under consideration: we are interested in equilibrium measures for Hölder potentials.
Definition 2.2. For a continuous function
![]() $\varsigma \colon N \to \mathbb {R}$
, we call a measure
$\varsigma \colon N \to \mathbb {R}$
, we call a measure
![]() $\nu $
an equilibrium state for
$\nu $
an equilibrium state for
![]() $g_t$
with potential
$g_t$
with potential
![]() $\varsigma $
if
$\varsigma $
if
![]() $\nu $
maximizes
$\nu $
maximizes
 $$ \begin{align*} \int_N \varsigma \, d\nu + h_\nu(g_1) \end{align*} $$
$$ \begin{align*} \int_N \varsigma \, d\nu + h_\nu(g_1) \end{align*} $$
among all
![]() $g_t$
-invariant probability measures on N. To emphasize the potential, we write
$g_t$
-invariant probability measures on N. To emphasize the potential, we write
![]() $\nu _\varsigma $
for the equilibrium state corresponding to
$\nu _\varsigma $
for the equilibrium state corresponding to
![]() $\varsigma $
when it exists and is unique.
$\varsigma $
when it exists and is unique.
Of particular importance to us is the fact that equilibrium states admit a local product structure with respect to the strong stable and unstable foliations, and that they are invariant under the appropriate transfer operators; we expand on both of these properties in due course.
When
![]() $g_t$
is an Anosov flow on a compact manifold, it is a classical result of Bowen and Ruelle [Reference Bowen and Ruelle7] that equilibrium states for Hölder potentials exist and are unique. Of course, the measure of maximal entropy is always an equilibrium state for the trivial potential
$g_t$
is an Anosov flow on a compact manifold, it is a classical result of Bowen and Ruelle [Reference Bowen and Ruelle7] that equilibrium states for Hölder potentials exist and are unique. Of course, the measure of maximal entropy is always an equilibrium state for the trivial potential
![]() $\varsigma = 0$
. In the case of the geodesic flow in negative curvature, the Liouville measure is the equilibrium state for the geometric potential
$\varsigma = 0$
. In the case of the geodesic flow in negative curvature, the Liouville measure is the equilibrium state for the geometric potential
 $$ \begin{align*} \varsigma (x) = -\frac d {dt}\bigg|_{t=0} (\log \| dg_t|_{W^u(x)}\|) \end{align*} $$
$$ \begin{align*} \varsigma (x) = -\frac d {dt}\bigg|_{t=0} (\log \| dg_t|_{W^u(x)}\|) \end{align*} $$
on the unit tangent bundle.
We are interested in extensions of Anosov flows that act fibrewise by isometries. Throughout, we assume that
![]() $g_t$
is a
$g_t$
is a
![]() $C^{2+\epsilon }$
flow whose strong stable and unstable distributions are
$C^{2+\epsilon }$
flow whose strong stable and unstable distributions are
![]() $C^1$
, so that the results of [Reference Dolgopyat11] apply.
$C^1$
, so that the results of [Reference Dolgopyat11] apply.
Definition 2.3. We call a smooth flow
![]() $f_t \colon (M,\mu ) \to (M,\mu )$
on a closed Riemannian manifold M a G-extension of
$f_t \colon (M,\mu ) \to (M,\mu )$
on a closed Riemannian manifold M a G-extension of
![]() $g_t \colon (N,\nu ) \to (N,\nu )$
if
$g_t \colon (N,\nu ) \to (N,\nu )$
if
![]() $\pi \colon M \to N$
is a smooth fibre bundle where:
$\pi \colon M \to N$
is a smooth fibre bundle where:
-
• the fibres
 $\pi ^{-1}(x)$
, with the induced metric, are all isometric to a closed Riemannian manifold F;
$\pi ^{-1}(x)$
, with the induced metric, are all isometric to a closed Riemannian manifold F; -
• G is a closed, connected normal subgroup of the isometry group
 $\operatorname {\mathrm {Isom}}(F)$
;
$\operatorname {\mathrm {Isom}}(F)$
; -
• G acts transitively on F and has no proper transitive normal subgroups;
-
•
 $\pi \circ f_t = g_t \circ \pi $
;
$\pi \circ f_t = g_t \circ \pi $
; -
• there is an atlas of trivializations of
 $\pi \colon M \to N$
for which all transition functions lie in G;
$\pi \colon M \to N$
for which all transition functions lie in G; -
• with respect to these trivializations, the isometries of F induced by the flow
 $f_t$
all lie in G;
$f_t$
all lie in G; -
•
 $f_t$
preserves a measure
$f_t$
preserves a measure
 $\mu $
satisfying
$\mu $
satisfying
 $\pi _*(\mu ) = \nu $
; and
$\pi _*(\mu ) = \nu $
; and -
• the fibrewise disintegration of
 $\mu $
along the fibres of
$\mu $
along the fibres of
 $\pi \colon M \to N$
is the pushforward of the normalized Haar measure on G to each fibre.
$\pi \colon M \to N$
is the pushforward of the normalized Haar measure on G to each fibre.
The primary driver of exponential mixing in our case will be a stronger variant of local accessibility.
Definition 2.4. Let
![]() $f_t \colon M \to M$
be a G-extension of
$f_t \colon M \to M$
be a G-extension of
![]() $g_t \colon N \to N$
. We call
$g_t \colon N \to N$
. We call
![]() $f_t$
locally G-accessible if, for every
$f_t$
locally G-accessible if, for every
![]() $\epsilon> 0$
, any trivialization
$\epsilon> 0$
, any trivialization
![]() $\phi \colon \pi ^{-1}(B_\epsilon (x)) \to B_\epsilon (x) \times F$
defined near
$\phi \colon \pi ^{-1}(B_\epsilon (x)) \to B_\epsilon (x) \times F$
defined near
![]() $x \in N$
and any isometry
$x \in N$
and any isometry
![]() $h \in G$
, there is a sequence of points
$h \in G$
, there is a sequence of points
![]() $x_0, \ldots , x_k \in N$
for which:
$x_0, \ldots , x_k \in N$
for which:
-
•
 $x_0 = x_k = x$
;
$x_0 = x_k = x$
; -
•
 $x_0, \ldots , x_k \in B_\epsilon (x)$
;
$x_0, \ldots , x_k \in B_\epsilon (x)$
; -
• we either have
 $x_{i+1} \in W^{su}_{g_t}(x_i)$
or
$x_{i+1} \in W^{su}_{g_t}(x_i)$
or
 $x_{i+1} \in W^{ss}_{g_t}(x_i)$
for each i; and
$x_{i+1} \in W^{ss}_{g_t}(x_i)$
for each i; and -
• we have
 $h = h_k^0 \circ \cdots \circ h_0^1$
, where
$h = h_k^0 \circ \cdots \circ h_0^1$
, where
 $h_i^{i+1} \colon F \to F$
is given (via
$h_i^{i+1} \colon F \to F$
is given (via
 $\phi $
) by the isometry
$\phi $
) by the isometry
 $\pi ^{-1}(x_i) \to \pi ^{-1}(x_{i+1})$
induced by leaves of the strong stable or strong unstable foliation of
$\pi ^{-1}(x_i) \to \pi ^{-1}(x_{i+1})$
induced by leaves of the strong stable or strong unstable foliation of
 $f_t$
.
$f_t$
.
2.2 Symbolic dynamics
In this section, we build a discrete, symbolic model for
![]() $f_t$
: we follow [Reference Sharp17], and accomplish this by artificially extending a standard Markov partition for the base flow. The results of [Reference Bowen6, Reference Ratner16] on the existence of Markov partitions for hyperbolic dynamical systems are classical and well-understood; as such, we recall some of the important points but refrain from delving into the details.
$f_t$
: we follow [Reference Sharp17], and accomplish this by artificially extending a standard Markov partition for the base flow. The results of [Reference Bowen6, Reference Ratner16] on the existence of Markov partitions for hyperbolic dynamical systems are classical and well-understood; as such, we recall some of the important points but refrain from delving into the details.
Theorem 2.2. (Bowen and Ratner)
If
![]() $g_t$
is Anosov, then
$g_t$
is Anosov, then
![]() $g_t$
has a Markov partition of size
$g_t$
has a Markov partition of size
![]() $\epsilon $
for any sufficiently small
$\epsilon $
for any sufficiently small
![]() $\epsilon> 0$
.
$\epsilon> 0$
.
Specifically, Bowen and Ratner constructed a Markov partition by taking local strong stable and unstable segments and forming a Markov rectangle.
Definition 2.5. Given
![]() $x \in N$
and
$x \in N$
and
![]() $\epsilon> 0$
, consider the local strong and weak stable and unstable manifolds of size
$\epsilon> 0$
, consider the local strong and weak stable and unstable manifolds of size
![]() $\epsilon $
through x given by
$\epsilon $
through x given by
 $$ \begin{align*} W^{ss}_\epsilon(x) &:= ( W^{ss}(x) \cap B_\epsilon(x) )^\circ,\ \ \quad W^{su}_\epsilon(x) := ( W^{su}(x) \cap B_\epsilon(x) )^\circ,\\ W^{ws}_\epsilon(x) &:= ( W^{ws}(x) \cap B_\epsilon(x) )^\circ,\quad W^{wu}_\epsilon(x) := ( W^{wu}(x) \cap B_\epsilon(x) )^\circ, \end{align*} $$
$$ \begin{align*} W^{ss}_\epsilon(x) &:= ( W^{ss}(x) \cap B_\epsilon(x) )^\circ,\ \ \quad W^{su}_\epsilon(x) := ( W^{su}(x) \cap B_\epsilon(x) )^\circ,\\ W^{ws}_\epsilon(x) &:= ( W^{ws}(x) \cap B_\epsilon(x) )^\circ,\quad W^{wu}_\epsilon(x) := ( W^{wu}(x) \cap B_\epsilon(x) )^\circ, \end{align*} $$
where in each case we have taken the connected component through x. For
![]() $u \in W^{su}_\epsilon (x)$
and
$u \in W^{su}_\epsilon (x)$
and
![]() $s \in W^{ss}_\epsilon (x)$
, we define the bracket of u and s to be the point of intersection
$s \in W^{ss}_\epsilon (x)$
, we define the bracket of u and s to be the point of intersection
which is necessarily unique when
![]() $\epsilon> 0$
is sufficiently small. We define the Markov rectangle
$\epsilon> 0$
is sufficiently small. We define the Markov rectangle
![]() $[W^{su}_\epsilon (x), W^{ss}_\epsilon (x)]$
to be the set
$[W^{su}_\epsilon (x), W^{ss}_\epsilon (x)]$
to be the set
assuming
![]() $\epsilon> 0$
is sufficiently small.
$\epsilon> 0$
is sufficiently small.
For now, fix
![]() $\epsilon> 0$
chosen to be small enough that a Markov partition exists; we will likely need to adjust our choice of
$\epsilon> 0$
chosen to be small enough that a Markov partition exists; we will likely need to adjust our choice of
![]() $\epsilon $
as we proceed. We let
$\epsilon $
as we proceed. We let
![]() $\mathcal R = \{ R_1, \ldots , R_k \}$
be a Markov partition of size
$\mathcal R = \{ R_1, \ldots , R_k \}$
be a Markov partition of size
![]() $\epsilon $
for
$\epsilon $
for
![]() $g_t$
, where each rectangle
$g_t$
, where each rectangle
![]() $R_i := [U_i,S_i]$
is generated by local strong stable and unstable manifolds
$R_i := [U_i,S_i]$
is generated by local strong stable and unstable manifolds
![]() $S_i := W^{ss}_\epsilon (z_i)$
and
$S_i := W^{ss}_\epsilon (z_i)$
and
![]() $U_i := W^{su}_\epsilon (z_i)$
through points
$U_i := W^{su}_\epsilon (z_i)$
through points
![]() $z_i \in N$
. Set
$z_i \in N$
. Set
![]() $R := \bigcup R_i$
,
$R := \bigcup R_i$
,
![]() $U := \bigcup U_i$
and
$U := \bigcup U_i$
and
![]() $S := \bigcup S_i$
.
$S := \bigcup S_i$
.
Remark 2.3. As we assumed that the strong stable and unstable foliations for
![]() $g_t$
were
$g_t$
were
![]() $C^1$
, each
$C^1$
, each
![]() $R_i$
is naturally an open
$R_i$
is naturally an open
![]() $C^1$
submanifold of N. It is important to note that both the Poincaré return map
$C^1$
submanifold of N. It is important to note that both the Poincaré return map
![]() $\mathcal P$
and the return time map
$\mathcal P$
and the return time map
![]() $\tau $
defined previously are the restrictions of locally
$\tau $
defined previously are the restrictions of locally
![]() $C^1$
functions on R, but both of these functions are discontinuous at points whose image would lie on the boundary of a Markov rectangle.
$C^1$
functions on R, but both of these functions are discontinuous at points whose image would lie on the boundary of a Markov rectangle.
To fix this, we remove any point of discontinuity for any iterate
![]() $\mathcal P^n$
and
$\mathcal P^n$
and
![]() $\tau ^{(n)}$
, and replace R with the corresponding full-measure residual subset
$\tau ^{(n)}$
, and replace R with the corresponding full-measure residual subset
![]() $R^*$
. Note that
$R^*$
. Note that
![]() $\mathcal P$
and
$\mathcal P$
and
![]() $\tau $
are both well defined on
$\tau $
are both well defined on
![]() $R^*$
, though we continue to reference R, U and S to make use of their
$R^*$
, though we continue to reference R, U and S to make use of their
![]() $C^1$
structure.
$C^1$
structure.
A more extensive discussion of this can be found in [Reference Chernov10, pp. 380–382]. We write
![]() $(\Sigma , \mathcal P)$
for the Markov shift corresponding to the partition
$(\Sigma , \mathcal P)$
for the Markov shift corresponding to the partition
![]() $\mathcal R$
of
$\mathcal R$
of
![]() $(N, g_t)$
.
$(N, g_t)$
.
Definition 2.6. The suspension of
![]() $(\Sigma , \mathcal P)$
with roof function
$(\Sigma , \mathcal P)$
with roof function
![]() $\tau $
is the flow
$\tau $
is the flow
![]() $g^{\prime }_t \colon \Sigma \times \mathbb {R}/\sim \to \Sigma \times \mathbb {R}/\sim $
defined by
$g^{\prime }_t \colon \Sigma \times \mathbb {R}/\sim \to \Sigma \times \mathbb {R}/\sim $
defined by
![]() $g^{\prime }_t(x, s) = (x, s + t)$
, where we have declared
$g^{\prime }_t(x, s) = (x, s + t)$
, where we have declared
![]() $(x, \tau (x)) \sim (\mathcal P(x), 0)$
.
$(x, \tau (x)) \sim (\mathcal P(x), 0)$
.
Theorem 2.2 states exactly that the natural inclusion of R into N induces a Hölder-continuous semi-conjugacy between
![]() $g_t$
and
$g_t$
and
![]() $g^{\prime }_t$
: this is precisely the result we wish to extend to
$g^{\prime }_t$
: this is precisely the result we wish to extend to
![]() $f_t$
.
$f_t$
.
Fix a finite cover
![]() $\{ V_i \}$
that trivializes the fibre bundle
$\{ V_i \}$
that trivializes the fibre bundle
![]() $\pi \colon M \to N$
, with isometries
$\pi \colon M \to N$
, with isometries
![]() $\phi _i \colon \pi ^{-1}(V_i) \to V_i \times F$
. At this point, we may need to revisit our choice of
$\phi _i \colon \pi ^{-1}(V_i) \to V_i \times F$
. At this point, we may need to revisit our choice of
![]() $\epsilon $
: let us assume that we have taken
$\epsilon $
: let us assume that we have taken
![]() $\epsilon $
to be smaller than the Lebesgue number of the cover
$\epsilon $
to be smaller than the Lebesgue number of the cover
![]() $\{ V_i \}$
. By definition, this means that each
$\{ V_i \}$
. By definition, this means that each
![]() $R_j$
lies entirely in some
$R_j$
lies entirely in some
![]() $V_{k(j)}$
and, hence,
$V_{k(j)}$
and, hence,
![]() $\phi _{k(j)}$
induces an isometry
$\phi _{k(j)}$
induces an isometry
 $\pi ^{-1}(R_j) \to R_j \times F$
. We can put these together to form an isometry
$\pi ^{-1}(R_j) \to R_j \times F$
. We can put these together to form an isometry
![]() $\phi \colon \pi ^{-1}(R) \to R \times F$
.
$\phi \colon \pi ^{-1}(R) \to R \times F$
.
It is worth noting that we have considerable freedom in our choice of isometries
![]() $\phi _i$
, and this is something we want to exploit to simplify our arguments in §4. As the centre-stable foliation of
$\phi _i$
, and this is something we want to exploit to simplify our arguments in §4. As the centre-stable foliation of
![]() $f_t$
is
$f_t$
is
![]() $C^1$
, we can modify a given
$C^1$
, we can modify a given
![]() $\phi _i$
so that it is constant along the (local) leaves of this foliation. Specifically, we assume that the projection of each
$\phi _i$
so that it is constant along the (local) leaves of this foliation. Specifically, we assume that the projection of each
![]() $\phi _i \colon \pi ^{-1}(V_i) \to V_i \times F$
onto F is constant on each connected component
$\phi _i \colon \pi ^{-1}(V_i) \to V_i \times F$
onto F is constant on each connected component
 $(W^{su}_{f_t}(x) \cap \pi ^{-1}(V_i))^\circ $
for each
$(W^{su}_{f_t}(x) \cap \pi ^{-1}(V_i))^\circ $
for each
![]() $x \in V_i$
.
$x \in V_i$
.
We realize
![]() $f_t$
as a suspension flow on
$f_t$
as a suspension flow on
![]() $\Sigma \times F$
with roof function
$\Sigma \times F$
with roof function
![]() $\tau $
. To do this, we need information on the fibrewise action of
$\tau $
. To do this, we need information on the fibrewise action of
![]() $g_t$
.
$g_t$
.
Definition 2.7. For
![]() $x \in R_{j_1} \cap R^*$
with
$x \in R_{j_1} \cap R^*$
with
![]() $\mathcal P(x) \in R_{j_2}$
, we define the temporal holonomy
$\mathcal P(x) \in R_{j_2}$
, we define the temporal holonomy
![]() $\operatorname {\mathrm {Hol}}(x)$
at x to be the isometry between
$\operatorname {\mathrm {Hol}}(x)$
at x to be the isometry between
 $\phi _{k(j_1)}(\pi ^{-1}(x))$
and
$\phi _{k(j_1)}(\pi ^{-1}(x))$
and
 $\phi _{k(j_2)}(\pi ^{-1}(\mathcal P(x)))$
induced by
$\phi _{k(j_2)}(\pi ^{-1}(\mathcal P(x)))$
induced by
![]() $f_t$
. This defines a function
$f_t$
. This defines a function
![]() $\operatorname {\mathrm {Hol}} \colon R^* \to G$
.
$\operatorname {\mathrm {Hol}} \colon R^* \to G$
.
We often write
![]() $\operatorname {\mathrm {Hol}}^{(n)}(x)$
for
$\operatorname {\mathrm {Hol}}^{(n)}(x)$
for
![]() $\operatorname {\mathrm {Hol}}(\mathcal P^{n-1}(x)) \circ \cdots \circ \operatorname {\mathrm {Hol}}(x)$
. Note that function composition is the multiplication operation in G.
$\operatorname {\mathrm {Hol}}(\mathcal P^{n-1}(x)) \circ \cdots \circ \operatorname {\mathrm {Hol}}(x)$
. Note that function composition is the multiplication operation in G.
Given the temporal holonomy function
![]() $\operatorname {\mathrm {Hol}} \colon R^* \to G$
, we can, of course, recover
$\operatorname {\mathrm {Hol}} \colon R^* \to G$
, we can, of course, recover
![]() $f_t$
as a suspension flow on
$f_t$
as a suspension flow on
![]() $(\Sigma \times F, \mathcal P \times \operatorname {\mathrm {Hol}})$
with roof function
$(\Sigma \times F, \mathcal P \times \operatorname {\mathrm {Hol}})$
with roof function
![]() $\tau $
. However, we push this a step further.
$\tau $
. However, we push this a step further.
We can define a projection along the leaves of the strong stable foliation
![]() $\operatorname {\mathrm {proj}}_S \colon R \to U$
by setting
$\operatorname {\mathrm {proj}}_S \colon R \to U$
by setting
![]() $\operatorname {\mathrm {proj}}_S([u,s]) = u$
. This allows us to construct a uniformly expanding model U for
$\operatorname {\mathrm {proj}}_S([u,s]) = u$
. This allows us to construct a uniformly expanding model U for
![]() $g_t$
, where the Poincaré return map
$g_t$
, where the Poincaré return map
![]() $\mathcal P \colon R^* \to R^*$
descends to a map
$\mathcal P \colon R^* \to R^*$
descends to a map
![]() $\sigma \colon U^* \to U^*$
given by
$\sigma \colon U^* \to U^*$
given by
![]() $\sigma := \operatorname {\mathrm {proj}}_S \circ \mathcal P$
.
$\sigma := \operatorname {\mathrm {proj}}_S \circ \mathcal P$
.
Remark 2.4. By construction, the return time map
![]() $\tau $
and the temporal holonomy function
$\tau $
and the temporal holonomy function
![]() $\operatorname {\mathrm {Hol}}$
are both constant along the leaves of the strong stable foliation of
$\operatorname {\mathrm {Hol}}$
are both constant along the leaves of the strong stable foliation of
![]() $g_t$
and, hence, descend to functions
$g_t$
and, hence, descend to functions
![]() $\tau \colon U \to \mathbb {R}$
and
$\tau \colon U \to \mathbb {R}$
and
![]() $\operatorname {\mathrm {Hol}} \colon U \to G$
.
$\operatorname {\mathrm {Hol}} \colon U \to G$
.
Set
![]() $U_{\tau } := U^* \times \mathbb {R} /{\sim} $
and
$U_{\tau } := U^* \times \mathbb {R} /{\sim} $
and
![]() $U_{\tau , \operatorname {\mathrm {Hol}}} := U^* \times \mathbb {R} \times F /{\sim} $
, where we declare
$U_{\tau , \operatorname {\mathrm {Hol}}} := U^* \times \mathbb {R} \times F /{\sim} $
, where we declare
![]() $(u, \tau (u)) \sim (\mathcal P(u), 0)$
and
$(u, \tau (u)) \sim (\mathcal P(u), 0)$
and
![]() $(u, \tau (u), k) \sim (\mathcal P(u), 0, (\operatorname {\mathrm {Hol}}(u))(k))$
, respectively. We write
$(u, \tau (u), k) \sim (\mathcal P(u), 0, (\operatorname {\mathrm {Hol}}(u))(k))$
, respectively. We write
![]() $f^{\prime }_t$
for the suspension flow
$f^{\prime }_t$
for the suspension flow
![]() $f^{\prime }_t(u, s, k) = (u, s+t, k)$
on
$f^{\prime }_t(u, s, k) = (u, s+t, k)$
on
![]() $U_{\tau ,\operatorname {\mathrm {Hol}}}$
. It is not too difficult to show that the exponential mixing of
$U_{\tau ,\operatorname {\mathrm {Hol}}}$
. It is not too difficult to show that the exponential mixing of
![]() $f_t$
is equivalent to exponential mixing for
$f_t$
is equivalent to exponential mixing for
![]() $f^{\prime }_t$
, though we must first fix a measure on
$f^{\prime }_t$
, though we must first fix a measure on
![]() $U_{\tau , \operatorname {\mathrm {Hol}}}$
to make sense of this.
$U_{\tau , \operatorname {\mathrm {Hol}}}$
to make sense of this.
Remark 2.5. As
![]() $\nu $
is an equilibrium state for a Hölder potential
$\nu $
is an equilibrium state for a Hölder potential
![]() $\phi $
, there are measures
$\phi $
, there are measures
![]() $\nu _i^s$
and
$\nu _i^s$
and
![]() $\nu _i^u$
on each of the strong stable and unstable segments
$\nu _i^u$
on each of the strong stable and unstable segments
![]() $S_i$
and
$S_i$
and
![]() $U_i$
so that
$U_i$
so that
![]() $\nu $
is absolutely continuous with respect to the product
$\nu $
is absolutely continuous with respect to the product
![]() $\nu _i^u \times \nu _i^s \times dt$
. Moreover, these measures can be chosen so that the Radon–Nikodym derivative of
$\nu _i^u \times \nu _i^s \times dt$
. Moreover, these measures can be chosen so that the Radon–Nikodym derivative of
![]() $\nu $
with respect to the product
$\nu $
with respect to the product
![]() $\nu _i^u \times \nu _i^s \times dt$
is uniformly bounded above by a constant
$\nu _i^u \times \nu _i^s \times dt$
is uniformly bounded above by a constant
![]() $K> 1$
and below by
$K> 1$
and below by
![]() $K^{-1} < 1$
. We write
$K^{-1} < 1$
. We write
![]() $\nu ^u$
and
$\nu ^u$
and
![]() $\nu ^s$
for the corresponding measures on U and S, respectively, and suppose that they have been normalized so that
$\nu ^s$
for the corresponding measures on U and S, respectively, and suppose that they have been normalized so that
![]() $\nu _U(U) = \nu _S(S) = 1$
.
$\nu _U(U) = \nu _S(S) = 1$
.
Remark 2.6. Up to replacing
![]() $\phi $
with a cohomologous function on
$\phi $
with a cohomologous function on
![]() $(\Sigma , \mathcal P)$
, we can assume that
$(\Sigma , \mathcal P)$
, we can assume that
![]() $\phi $
is the extension of a Hölder potential
$\phi $
is the extension of a Hölder potential
![]() $\phi ^U$
on U. As a consequence, we may as well assume that
$\phi ^U$
on U. As a consequence, we may as well assume that
![]() $\nu ^u$
is, in fact, an equilibrium state for a Hölder potential
$\nu ^u$
is, in fact, an equilibrium state for a Hölder potential
![]() $\phi ^U$
on
$\phi ^U$
on
![]() $(U, \sigma )$
.
$(U, \sigma )$
.
These are classical results in thermodynamic formalism: we refer the reader to [Reference Leplaideur15] and [Reference Sugiura18, pp. 87–91], respectively, for more details. We require, in addition, the conditional measure
![]() $\nu ^u$
to have a doubling property later on, in order to control the spectrum of our transfer operators using Dolgopyat’s methods.
$\nu ^u$
to have a doubling property later on, in order to control the spectrum of our transfer operators using Dolgopyat’s methods.
Definition 2.8. We say that a measure
![]() $\nu ^u$
has the doubling or Federer property, or is diametrically regular, if for any
$\nu ^u$
has the doubling or Federer property, or is diametrically regular, if for any
![]() $k> 1$
there is a uniform constant
$k> 1$
there is a uniform constant
![]() $C> 0$
so that
$C> 0$
so that
for all
![]() $x \in U$
and
$x \in U$
and
![]() $r> 0$
.
$r> 0$
.
It is important to note that
![]() $U_{\tau , \operatorname {\mathrm {Hol}}}$
has no natural smooth structure, and
$U_{\tau , \operatorname {\mathrm {Hol}}}$
has no natural smooth structure, and
![]() $U^*$
may well have infinitely many connected components. However, we understand
$U^*$
may well have infinitely many connected components. However, we understand
![]() $C^1(U_{\tau ,\operatorname {\mathrm {Hol}}}, \mathbb {C})$
to mean the class of functions on
$C^1(U_{\tau ,\operatorname {\mathrm {Hol}}}, \mathbb {C})$
to mean the class of functions on
![]() $U_{\tau ,\operatorname {\mathrm {Hol}}}$
, identified as a quotient of
$U_{\tau ,\operatorname {\mathrm {Hol}}}$
, identified as a quotient of
![]() $U^* \times \mathbb {R} \times F /{\sim }$
, that arise as the restriction of a smooth function on
$U^* \times \mathbb {R} \times F /{\sim }$
, that arise as the restriction of a smooth function on
![]() $U \times \mathbb {R} \times F$
. It is easy to see that the symbolic flow
$U \times \mathbb {R} \times F$
. It is easy to see that the symbolic flow
![]() $f^{\prime }_t$
leaves invariant
$f^{\prime }_t$
leaves invariant
![]() $C^1(U_{\tau ,\operatorname {\mathrm {Hol}}}, \mathbb {C})$
defined in this way.
$C^1(U_{\tau ,\operatorname {\mathrm {Hol}}}, \mathbb {C})$
defined in this way.
With the following lemma, we restrict ourselves to establishing exponential mixing for the suspension flow
![]() $f^{\prime }_t$
on the expanding model
$f^{\prime }_t$
on the expanding model
![]() $U_{\tau ,\operatorname {\mathrm {Hol}}}$
.
$U_{\tau ,\operatorname {\mathrm {Hol}}}$
.
Lemma 2.7. If
![]() $f^{\prime }_t$
is exponentially mixing of order k for functions in
$f^{\prime }_t$
is exponentially mixing of order k for functions in
![]() $C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
, then
$C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
, then
![]() $f_t$
is exponentially mixing of order k for functions in
$f_t$
is exponentially mixing of order k for functions in
![]() $C^1(M, \mathbb {C})$
.
$C^1(M, \mathbb {C})$
.
Proof. Once again, we perform the argument in the case
![]() $k = 1$
. The general case can be obtained by repeating this inductively. Given
$k = 1$
. The general case can be obtained by repeating this inductively. Given
![]() $\varphi , \psi \in C^1(M, \mathbb {C})$
with
$\varphi , \psi \in C^1(M, \mathbb {C})$
with
![]() $\int _M \varphi \, d\mu = \int _M \psi \, d\mu = 0$
and a fixed
$\int _M \varphi \, d\mu = \int _M \psi \, d\mu = 0$
and a fixed
![]() $k \in F$
, we consider corresponding functions
$k \in F$
, we consider corresponding functions
![]() $\varphi _t, \psi _t \in C^1(U_{\tau ,\operatorname {\mathrm {Hol}}},\mathbb {C})$
given by
$\varphi _t, \psi _t \in C^1(U_{\tau ,\operatorname {\mathrm {Hol}}},\mathbb {C})$
given by
 $$ \begin{align*} \varphi_t (u, h, r) &:= \int_{S} \varphi( f_{t+r}( \phi^{-1}( [u,s], h(k) ) ) ) \, d\nu^s,\\ \psi_t (u, h, r) &:= \int_{S} \psi( f_{t+r}( \phi^{-1}( [u,s], h(k) ) ) ) \, d\nu^s, \end{align*} $$
$$ \begin{align*} \varphi_t (u, h, r) &:= \int_{S} \varphi( f_{t+r}( \phi^{-1}( [u,s], h(k) ) ) ) \, d\nu^s,\\ \psi_t (u, h, r) &:= \int_{S} \psi( f_{t+r}( \phi^{-1}( [u,s], h(k) ) ) ) \, d\nu^s, \end{align*} $$
for each t. Let
![]() $C_0q^t$
be the rate of contraction of S under
$C_0q^t$
be the rate of contraction of S under
![]() $g_t$
. As
$g_t$
. As
![]() $\varphi $
is
$\varphi $
is
![]() $C^1$
,
$C^1$
,
 $$ \begin{align*} | \varphi(f_{t+r}(\phi^{-1}([u,s],h(k))) - \varphi(f_{t+r}(\phi^{-1}([u,s_0],h(k))) | < C_0 q^t\|\varphi\|_{C^1} \end{align*} $$
$$ \begin{align*} | \varphi(f_{t+r}(\phi^{-1}([u,s],h(k))) - \varphi(f_{t+r}(\phi^{-1}([u,s_0],h(k))) | < C_0 q^t\|\varphi\|_{C^1} \end{align*} $$
for any
![]() $s_0 \in S$
. Of course, this yields
$s_0 \in S$
. Of course, this yields
 $$ \begin{align*} &\bigg| \int_S \varphi(f_{t+r}(\phi^{-1}([u,s],h(k))) \, d\nu^s - \int_S \varphi(f_{t+r}(\phi^{-1}([u,s_0],h(k))) \, d\nu^s \bigg|\\ &\quad< C_0 q^t\|\varphi\|_{C^1} \nu^s(S) \end{align*} $$
$$ \begin{align*} &\bigg| \int_S \varphi(f_{t+r}(\phi^{-1}([u,s],h(k))) \, d\nu^s - \int_S \varphi(f_{t+r}(\phi^{-1}([u,s_0],h(k))) \, d\nu^s \bigg|\\ &\quad< C_0 q^t\|\varphi\|_{C^1} \nu^s(S) \end{align*} $$
after simply integrating both sides with respect to s. This can be rewritten as
 $$ \begin{align*} &\bigg| \int_S \varphi(f_{t+r}(\phi^{-1}([u,s],h(k))) \, d\nu^s - \varphi(f_{t+r}(\phi^{-1}([u,s_0],h(k))) \cdot \nu^s(S) \bigg|\\ &\quad< C_0 q^t\|\varphi\|_{C^1} \nu^s(S) \end{align*} $$
$$ \begin{align*} &\bigg| \int_S \varphi(f_{t+r}(\phi^{-1}([u,s],h(k))) \, d\nu^s - \varphi(f_{t+r}(\phi^{-1}([u,s_0],h(k))) \cdot \nu^s(S) \bigg|\\ &\quad< C_0 q^t\|\varphi\|_{C^1} \nu^s(S) \end{align*} $$
because
![]() $s_0$
is fixed. We then see quickly that the difference in the integrals
$s_0$
is fixed. We then see quickly that the difference in the integrals
 $$ \begin{align} &\int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \bigg(\int_{S} \varphi( f_{t+r}( \phi^{-1}( [u,s], h(k) ) ) ) \, d\nu^s(s) \bigg)\notag\\ &\quad\cdot \bigg(\int_{S} \psi( f_{r}( \phi^{-1}( [u,s'], h(k) ) ) ) \, d\nu^s(s')\bigg) \, d\omega \, dr \, d\nu^u \end{align} $$
$$ \begin{align} &\int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \bigg(\int_{S} \varphi( f_{t+r}( \phi^{-1}( [u,s], h(k) ) ) ) \, d\nu^s(s) \bigg)\notag\\ &\quad\cdot \bigg(\int_{S} \psi( f_{r}( \phi^{-1}( [u,s'], h(k) ) ) ) \, d\nu^s(s')\bigg) \, d\omega \, dr \, d\nu^u \end{align} $$
and
 $$ \begin{align} &\nu^s(S)\int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \int_{S} \varphi( f_{t+r}( \phi^{-1}( [u,s_0],h(k) ) ) )\notag\\ &\quad\cdot \psi( f_{r}( \phi^{-1}( [u,s'], h(k) ) ) ) \, d\nu^s(s')\, d\omega \, dr \, d\nu^u \end{align} $$
$$ \begin{align} &\nu^s(S)\int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \int_{S} \varphi( f_{t+r}( \phi^{-1}( [u,s_0],h(k) ) ) )\notag\\ &\quad\cdot \psi( f_{r}( \phi^{-1}( [u,s'], h(k) ) ) ) \, d\nu^s(s')\, d\omega \, dr \, d\nu^u \end{align} $$
is at most
![]() $C_1q^t \|\varphi \|_{C^1} \|\psi \|_{C^0}$
. But now, the same argument shows that
$C_1q^t \|\varphi \|_{C^1} \|\psi \|_{C^0}$
. But now, the same argument shows that
and
must be within
![]() $C_2q^t \|\varphi \|_{C^1} \|\psi \|_{C^0}$
of each other. Hence,
$C_2q^t \|\varphi \|_{C^1} \|\psi \|_{C^0}$
of each other. Hence,
 $$ \begin{align*} &\nu^s(S)\int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \int_{S} \varphi( f_{t+r}( \phi^{-1}( [u,s'],h(k) ) ) )\\&\quad\cdot \psi( f_{r}( \phi^{-1}( [u,s'], h(k) ) ) ) d\nu^s(s')\, d\omega \, dr \, d\nu^u \end{align*} $$
$$ \begin{align*} &\nu^s(S)\int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \int_{S} \varphi( f_{t+r}( \phi^{-1}( [u,s'],h(k) ) ) )\\&\quad\cdot \psi( f_{r}( \phi^{-1}( [u,s'], h(k) ) ) ) d\nu^s(s')\, d\omega \, dr \, d\nu^u \end{align*} $$
is within
![]() $C_3 q^t \|\varphi \|_{C^1} \|\psi \|_{C^0}$
of (2.2). From the local product structure of
$C_3 q^t \|\varphi \|_{C^1} \|\psi \|_{C^0}$
of (2.2). From the local product structure of
![]() $\nu $
, we see that this is within a constant multiplicative factor of K of the integral
$\nu $
, we see that this is within a constant multiplicative factor of K of the integral
 $$ \begin{align} \int_M \varphi(f_t(x)) \cdot \psi(x) \, d\mu \end{align} $$
$$ \begin{align} \int_M \varphi(f_t(x)) \cdot \psi(x) \, d\mu \end{align} $$
for any
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
. To conclude, we simply observe that if
$\psi $
. To conclude, we simply observe that if
![]() $\int _M \varphi \, d\mu = \int _M \psi \, d\mu = 0$
, then we must have
$\int _M \varphi \, d\mu = \int _M \psi \, d\mu = 0$
, then we must have
 $$ \begin{align*} \int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \varphi_t(u,h,r) \, d\omega \, dr \, d\nu^u = \int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \psi_t (u,h,r) \, d\omega \, dr \, d\nu^u = 0 \end{align*} $$
$$ \begin{align*} \int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \varphi_t(u,h,r) \, d\omega \, dr \, d\nu^u = \int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \psi_t (u,h,r) \, d\omega \, dr \, d\nu^u = 0 \end{align*} $$
for any
![]() $t \in \mathbb {R}$
. Moreover, the regularity of
$t \in \mathbb {R}$
. Moreover, the regularity of
![]() $\varphi _t$
and
$\varphi _t$
and
![]() $\psi _t$
is determined by the regularity of the bracket operation
$\psi _t$
is determined by the regularity of the bracket operation
![]() $[\cdot ,\cdot ]$
: because we assumed that the foliations were
$[\cdot ,\cdot ]$
: because we assumed that the foliations were
![]() $C^1$
, we see that
$C^1$
, we see that
![]() $\varphi _t$
and
$\varphi _t$
and
![]() $\psi _t$
must also be
$\psi _t$
must also be
![]() $C^1$
. Hence, if
$C^1$
. Hence, if
![]() $f^{\prime }_t$
is exponentially mixing for functions in
$f^{\prime }_t$
is exponentially mixing for functions in
![]() $C^1(U_{\tau ,\operatorname {\mathrm {Hol}}},\mathbb {C})$
, (2.1) must decay exponentially in t, from which we conclude that (2.3) must also decay exponentially.
$C^1(U_{\tau ,\operatorname {\mathrm {Hol}}},\mathbb {C})$
, (2.1) must decay exponentially in t, from which we conclude that (2.3) must also decay exponentially.
2.3 Representation theory
In this section, we recall some classical results from the representation theory and harmonic analysis of compact Lie groups; our primary references are [Reference Applebaum2, Reference Sarkar and Winter19].
Following [Reference Sharp17, §3.6], our strategy is to decompose functions on
![]() $U_{\tau , \operatorname {\mathrm {Hol}}}$
into components corresponding to irreducible representations of G. A function
$U_{\tau , \operatorname {\mathrm {Hol}}}$
into components corresponding to irreducible representations of G. A function
![]() $\varphi \in C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
can be viewed as a
$\varphi \in C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
can be viewed as a
![]() $C^1$
function
$C^1$
function
![]() $\tilde \varphi \colon U_{\tau } \to L^2(G)$
by setting
$\tilde \varphi \colon U_{\tau } \to L^2(G)$
by setting
![]() $\tilde \varphi (u, r) := \varphi (u, \cdot , r)$
.
$\tilde \varphi (u, r) := \varphi (u, \cdot , r)$
.
As G is a compact, connected Lie group, we can decompose
![]() $\tilde \varphi (u, r) \in L^2(G)$
into isotypic components corresponding to irreducible representations of G: this is, of course, the classical Peter–Weyl theorem.
$\tilde \varphi (u, r) \in L^2(G)$
into isotypic components corresponding to irreducible representations of G: this is, of course, the classical Peter–Weyl theorem.
Theorem 2.8. (Peter–Weyl)
If G is a compact, connected Lie group, then there is a decomposition
 $$ \begin{align*} L^2(G) = \bigoplus_\rho (V^\rho)^{\oplus \dim \rho}, \end{align*} $$
$$ \begin{align*} L^2(G) = \bigoplus_\rho (V^\rho)^{\oplus \dim \rho}, \end{align*} $$
where the sum is taken over pairwise non-isomorphic irreducible representations of G, and the
![]() $(V^\rho ){\oplus \dim \rho }$
associated with non-isomorphic irreducible representations are pairwise orthogonal with respect to the standard inner product on
$(V^\rho ){\oplus \dim \rho }$
associated with non-isomorphic irreducible representations are pairwise orthogonal with respect to the standard inner product on
![]() $L^2(G)$
.
$L^2(G)$
.
We fix such a decomposition and write
 $\tilde \varphi (u,r) = \sum _\rho \tilde \varphi ^\rho (u, r)$
for the decomposition of
$\tilde \varphi (u,r) = \sum _\rho \tilde \varphi ^\rho (u, r)$
for the decomposition of
![]() $\tilde \varphi (u,r)$
obtained by projecting onto each
$\tilde \varphi (u,r)$
obtained by projecting onto each
![]() $(V^\rho ){\oplus \dim \rho }$
. Abusing notation, we use
$(V^\rho ){\oplus \dim \rho }$
. Abusing notation, we use
![]() $\varphi $
to refer interchangeably to a function
$\varphi $
to refer interchangeably to a function
![]() $U_\tau \to L^2(G)$
or to the function
$U_\tau \to L^2(G)$
or to the function
![]() $U_{\tau , \operatorname {\mathrm {Hol}}} \to \mathbb {C}$
; there should be little ambiguity in either case.
$U_{\tau , \operatorname {\mathrm {Hol}}} \to \mathbb {C}$
; there should be little ambiguity in either case.
For our later analysis, it is helpful to consider the derived representation
![]() $d\rho $
of the Lie algebra
$d\rho $
of the Lie algebra
![]() $\mathfrak g$
of G acting on
$\mathfrak g$
of G acting on
![]() $L^2(G)$
, induced by the representation
$L^2(G)$
, induced by the representation
![]() $\rho $
of G on
$\rho $
of G on
![]() $L^2(G)$
: see [Reference Applebaum2, §2.5.1] for details. We always assume that we have a fixed
$L^2(G)$
: see [Reference Applebaum2, §2.5.1] for details. We always assume that we have a fixed
![]() $\operatorname {\mathrm {Ad}}$
-invariant norm
$\operatorname {\mathrm {Ad}}$
-invariant norm
![]() $\| \cdot \|_{\mathfrak g}$
on
$\| \cdot \|_{\mathfrak g}$
on
![]() $\mathfrak g$
.
$\mathfrak g$
.
Definition 2.9. Given an irreducible representation
![]() $\rho \colon G \to \operatorname {\mathrm {GL}}(V^\rho )$
of G (where we view
$\rho \colon G \to \operatorname {\mathrm {GL}}(V^\rho )$
of G (where we view
![]() $V^\rho \subset L^2(G)$
), we define the norm
$V^\rho \subset L^2(G)$
), we define the norm
![]() $\|\rho \|$
of
$\|\rho \|$
of
![]() $\rho $
to be the supremum
$\rho $
to be the supremum
 $$ \begin{align*} \|\rho\| := \sup_{\|X\|_{\mathfrak g} = 1} \|d\rho(X)\|_{L^2(G)} \end{align*} $$
$$ \begin{align*} \|\rho\| := \sup_{\|X\|_{\mathfrak g} = 1} \|d\rho(X)\|_{L^2(G)} \end{align*} $$
where
![]() $\|d\rho (X)\|_{L^2(G)}$
is the operator norm of
$\|d\rho (X)\|_{L^2(G)}$
is the operator norm of
![]() $d\rho (X)$
viewed as an automorphism of
$d\rho (X)$
viewed as an automorphism of
![]() $L^2(G)$
.
$L^2(G)$
.
It is a classical fact that
![]() $\|\rho \|$
is finite, and can be bounded in terms of the highest weight associated with
$\|\rho \|$
is finite, and can be bounded in terms of the highest weight associated with
![]() $\rho $
. In the following propositions, let
$\rho $
. In the following propositions, let
![]() $|\lambda |$
denote the norm of a weight
$|\lambda |$
denote the norm of a weight
![]() $\lambda $
arising from a fixed
$\lambda $
arising from a fixed
![]() $\operatorname {\mathrm {ad}}_{\mathfrak g}$
-invariant inner product
$\operatorname {\mathrm {ad}}_{\mathfrak g}$
-invariant inner product
![]() $\langle \cdot , \cdot \rangle $
on the Lie algebra
$\langle \cdot , \cdot \rangle $
on the Lie algebra
![]() $\mathfrak g$
.
$\mathfrak g$
.
Proposition 2.9. Let
![]() $\rho $
be a non-trivial irreducible representation, and let
$\rho $
be a non-trivial irreducible representation, and let
![]() $\lambda (\rho )$
be its highest weight. There are uniform constants
$\lambda (\rho )$
be its highest weight. There are uniform constants
![]() $C> 0$
and
$C> 0$
and
![]() $m> 0$
so that
$m> 0$
so that
Proof. See [Reference Applebaum2, Theorem 3.4.1]; note that the Hilbert–Schmidt norm is an upper bound for the operator norm.
We also require some particular results on the growth rate of
![]() $\|\rho \|$
.
$\|\rho \|$
.
Proposition 2.10. There is a constant
![]() $N> 0$
so that the sum
$N> 0$
so that the sum
![]() $\sum _\rho \|\rho \|^{-n}$
taken over non-trivial irreducible representations
$\sum _\rho \|\rho \|^{-n}$
taken over non-trivial irreducible representations
![]() $\rho $
of G converges for any
$\rho $
of G converges for any
![]() $n \geq N$
.
$n \geq N$
.
Proof. By Proposition 2.9, we can bound
 $$ \begin{align*} \sum_\rho \|\rho\|^{-n} \leq C^{-n}\sum_\rho |\lambda(\rho)|^{-( m/ n)}, \end{align*} $$
$$ \begin{align*} \sum_\rho \|\rho\|^{-n} \leq C^{-n}\sum_\rho |\lambda(\rho)|^{-( m/ n)}, \end{align*} $$
which, by [Reference Applebaum2, Theorem 3.2.1], converges so long as
![]() $ m/n$
exceeds the rank of G.
$ m/n$
exceeds the rank of G.
More generally, we can obtain decay estimates for the Fourier coefficients
![]() $\varphi ^\rho $
associated with irreducible representations
$\varphi ^\rho $
associated with irreducible representations
![]() $\rho $
.
$\rho $
.
Theorem 2.11. For every
![]() $n> {\dim (G)}/4$
, there is a
$n> {\dim (G)}/4$
, there is a
![]() $C> 0$
so that
$C> 0$
so that
for all non-trivial irreducible representations
![]() $\rho $
of G and all
$\rho $
of G and all
![]() $\varphi \in C^{2n}(U_\tau , L^2(G))$
.
$\varphi \in C^{2n}(U_\tau , L^2(G))$
.
Proof. By [Reference Sarkar and Winter19, equations (1.5) and (1.11)], we have the inequality
 $$ \begin{align*} \|\lambda(\rho)\|^{2k}\|\varphi^\rho\|_{L^2(G)} \leq \|\varphi\|_{C^k} \end{align*} $$
$$ \begin{align*} \|\lambda(\rho)\|^{2k}\|\varphi^\rho\|_{L^2(G)} \leq \|\varphi\|_{C^k} \end{align*} $$
for any
![]() $\varphi \in C^{2k}(U_\tau , L^2(G))$
and
$\varphi \in C^{2k}(U_\tau , L^2(G))$
and
![]() $2k> {\dim (G)}/ 2$
. By Proposition 2.9, we therefore have
$2k> {\dim (G)}/ 2$
. By Proposition 2.9, we therefore have
 $$ \begin{align*} \|\rho\|^{ {2k}/ m} \|\varphi^\rho\|_{L^2(G)} \leq C^{ {2k}/ m} \|\varphi\|_{C^k} \end{align*} $$
$$ \begin{align*} \|\rho\|^{ {2k}/ m} \|\varphi^\rho\|_{L^2(G)} \leq C^{ {2k}/ m} \|\varphi\|_{C^k} \end{align*} $$
for some uniform
![]() $m> 0$
, from which the theorem follows.
$m> 0$
, from which the theorem follows.
3 Twisted transfer operators
In this section, we define Dolgopyat’s ‘twisted’ transfer operators, and show how the spectral bounds we intend to obtain for these operators lead to correlation decay estimates for the expanding suspension semi-flow
![]() $f^{\prime }_t$
constructed in the previous section.
$f^{\prime }_t$
constructed in the previous section.
Recall that we can view a smooth function
![]() $\psi \in C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
as a function
$\psi \in C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
as a function
![]() $\psi \in C^1(U_\tau , L^2(G))$
. We can integrate out the time variable to obtain
$\psi \in C^1(U_\tau , L^2(G))$
. We can integrate out the time variable to obtain
 $$ \begin{align*} \tilde\psi(u) := \int_0^{\tau(u)} \psi(u,r) \, dr \end{align*} $$
$$ \begin{align*} \tilde\psi(u) := \int_0^{\tau(u)} \psi(u,r) \, dr \end{align*} $$
in
![]() $C^1(U, L^2(G))$
; this is the space on which we would like to define our operators. The advantages of working with smooth (as opposed to Hölder) functions will become clear in §5, but we need to assume that
$C^1(U, L^2(G))$
; this is the space on which we would like to define our operators. The advantages of working with smooth (as opposed to Hölder) functions will become clear in §5, but we need to assume that
![]() $\varsigma $
is
$\varsigma $
is
![]() $C^1$
for most of our arguments. We explain how to modify our proof to deal with the general case where
$C^1$
for most of our arguments. We explain how to modify our proof to deal with the general case where
![]() $\varsigma $
is Hölder in Corollary 5.8, using a standard approximation argument.
$\varsigma $
is Hölder in Corollary 5.8, using a standard approximation argument.
Let
![]() $\rho $
be an irreducible representation of G acting on an isotypic component
$\rho $
be an irreducible representation of G acting on an isotypic component
![]() $V^\rho \subset L^2(G)$
, and fix
$V^\rho \subset L^2(G)$
, and fix
![]() $z \in \mathbb {C}$
. We define the transfer operator
$z \in \mathbb {C}$
. We define the transfer operator
 $\skew3\tilde {\mathcal L}_{z,\rho } \colon C^1(U,V^\rho ) \to C^1(U,V^\rho )$
by
$\skew3\tilde {\mathcal L}_{z,\rho } \colon C^1(U,V^\rho ) \to C^1(U,V^\rho )$
by
 $$ \begin{align*} ( \skew3\tilde {\mathcal L}_{z,\rho} \varphi )(u) := \sum_{\sigma(u') = u} e^{\varsigma_z(u')} ( \rho(\operatorname{\mathrm{Hol}}(u')) \cdot \varphi(u') ), \end{align*} $$
$$ \begin{align*} ( \skew3\tilde {\mathcal L}_{z,\rho} \varphi )(u) := \sum_{\sigma(u') = u} e^{\varsigma_z(u')} ( \rho(\operatorname{\mathrm{Hol}}(u')) \cdot \varphi(u') ), \end{align*} $$
where
![]() $\varsigma _z$
is the potential on the one-sided Markov model
$\varsigma _z$
is the potential on the one-sided Markov model
![]() $(\Sigma ^+, \sigma )$
obtained as the restriction of the potential
$(\Sigma ^+, \sigma )$
obtained as the restriction of the potential
 $$ \begin{align*} \int_0^{\tau(u)} (\varsigma \circ p)(u,s,t) \, dt - z \cdot \tau(u,s) \end{align*} $$
$$ \begin{align*} \int_0^{\tau(u)} (\varsigma \circ p)(u,s,t) \, dt - z \cdot \tau(u,s) \end{align*} $$
defined on
![]() $(\Sigma , \mathcal P)$
. Note that
$(\Sigma , \mathcal P)$
. Note that
![]() $\varsigma _z$
is well-defined in light of Remark 2.6, where we assumed that both
$\varsigma _z$
is well-defined in light of Remark 2.6, where we assumed that both
![]() $\alpha $
and
$\alpha $
and
![]() $\tau $
are constant in s. It is also worth remarking that both
$\tau $
are constant in s. It is also worth remarking that both
![]() $\tau $
and p are
$\tau $
and p are
![]() $C^1$
, because we assumed that the strong stable and unstable foliations of
$C^1$
, because we assumed that the strong stable and unstable foliations of
![]() $g_t$
were
$g_t$
were
![]() $C^1$
. As a consequence,
$C^1$
. As a consequence,
![]() $\varsigma _z$
and, hence,
$\varsigma _z$
and, hence,
 $\skew3\tilde {\mathcal L}_{z,\rho }\varphi $
are both
$\skew3\tilde {\mathcal L}_{z,\rho }\varphi $
are both
![]() $C^1$
, because we have restricted ourselves to the case where
$C^1$
, because we have restricted ourselves to the case where
![]() $\varsigma $
is smooth.
$\varsigma $
is smooth.
Let us recall some classical results of thermodynamic formalism; for a slightly more detailed treatment, we refer the reader to [Reference Sugiura18, pp. 87–91]. Let
![]() $P(\varsigma )$
be the topological pressure of
$P(\varsigma )$
be the topological pressure of
![]() $\varsigma $
for the map
$\varsigma $
for the map
![]() $g_1$
. By the Ruelle–Perron–Frobenius theorem, the operator
$g_1$
. By the Ruelle–Perron–Frobenius theorem, the operator
 $\skew3\tilde {\mathcal L}_{P(\varsigma ),0}$
associated with the trivial representation
$\skew3\tilde {\mathcal L}_{P(\varsigma ),0}$
associated with the trivial representation
![]() $\rho = 0$
has a unique positive eigenvector
$\rho = 0$
has a unique positive eigenvector
![]() $\varphi _\varsigma \in C^1(U, \mathbb {R})$
with eigenvalue
$\varphi _\varsigma \in C^1(U, \mathbb {R})$
with eigenvalue
![]() $e^{P(\varsigma )}$
.
$e^{P(\varsigma )}$
.
Recall that
![]() $\nu ^u$
is an equilibrium measure for the restriction of the potential
$\nu ^u$
is an equilibrium measure for the restriction of the potential
![]() $\varsigma $
to
$\varsigma $
to
![]() $(\Sigma ^+, \sigma )$
, which by construction has the same topological pressure
$(\Sigma ^+, \sigma )$
, which by construction has the same topological pressure
![]() $P(\varsigma )$
. By the Lanford–Ruelle variational principle, this means that
$P(\varsigma )$
. By the Lanford–Ruelle variational principle, this means that
 $$ \begin{align*} e^{P(\varsigma)} \int_U \varphi \, d\nu^u = \int_U \skew3\tilde {\mathcal L}_{P(\varsigma),0}\varphi \, d\nu^u \end{align*} $$
$$ \begin{align*} e^{P(\varsigma)} \int_U \varphi \, d\nu^u = \int_U \skew3\tilde {\mathcal L}_{P(\varsigma),0}\varphi \, d\nu^u \end{align*} $$
for all
![]() $\varphi \in C^1(U, V^\rho )$
. It will be convenient to normalize
$\varphi \in C^1(U, V^\rho )$
. It will be convenient to normalize
 $\skew3\tilde {\mathcal L}_{P(\varsigma ),0}\varphi $
so that it preserves the measure
$\skew3\tilde {\mathcal L}_{P(\varsigma ),0}\varphi $
so that it preserves the measure
![]() $\nu ^u$
: let
$\nu ^u$
: let
![]() $\mathcal L_{z,\rho }$
be the operator defined by
$\mathcal L_{z,\rho }$
be the operator defined by
 $$ \begin{align*} (\mathcal L_{z,\rho} \varphi)(u) := \varphi_\varsigma(u)\frac{( \skew3\tilde {\mathcal L}_{z,\rho} (\varphi \cdot \varphi_\varsigma^{-1}) )(u)}{e^{P(\varsigma)}} \end{align*} $$
$$ \begin{align*} (\mathcal L_{z,\rho} \varphi)(u) := \varphi_\varsigma(u)\frac{( \skew3\tilde {\mathcal L}_{z,\rho} (\varphi \cdot \varphi_\varsigma^{-1}) )(u)}{e^{P(\varsigma)}} \end{align*} $$
for all
![]() $\varphi \in C^1(U, V^\rho )$
.
$\varphi \in C^1(U, V^\rho )$
.
Remark 3.1. With these renormalizations, we have
 $$ \begin{align*} \int_U \varphi \, d\nu^u = \int_U \mathcal L_{P(\varsigma),0}\varphi \, d\nu^u \end{align*} $$
$$ \begin{align*} \int_U \varphi \, d\nu^u = \int_U \mathcal L_{P(\varsigma),0}\varphi \, d\nu^u \end{align*} $$
for all
![]() $\varphi \in C^1(U,\mathbb {R})$
.
$\varphi \in C^1(U,\mathbb {R})$
.
We can alternatively write
 $$ \begin{align*} (\mathcal L_{z,\rho}\varphi)(u) = \sum_{\sigma(u')=u} e^{\alpha_z(u')} (\rho(\operatorname{\mathrm{Hol}}(u')) \cdot \varphi(u')), \end{align*} $$
$$ \begin{align*} (\mathcal L_{z,\rho}\varphi)(u) = \sum_{\sigma(u')=u} e^{\alpha_z(u')} (\rho(\operatorname{\mathrm{Hol}}(u')) \cdot \varphi(u')), \end{align*} $$
where we set
 $$ \begin{align*} \alpha_z(u) &:= \int_0^{\tau(u)} (\varsigma \circ p) (u,s,t) \, dt - z \cdot \tau(u,s)\\ &\quad- \log (\varphi_\varsigma(u)) + \log (\varphi_\varsigma(\sigma(u))) - \log P(\varsigma) \end{align*} $$
$$ \begin{align*} \alpha_z(u) &:= \int_0^{\tau(u)} (\varsigma \circ p) (u,s,t) \, dt - z \cdot \tau(u,s)\\ &\quad- \log (\varphi_\varsigma(u)) + \log (\varphi_\varsigma(\sigma(u))) - \log P(\varsigma) \end{align*} $$
for all
![]() $u \in U$
: note that the positivity of
$u \in U$
: note that the positivity of
![]() $\varphi _\varsigma $
is required to ensure that
$\varphi _\varsigma $
is required to ensure that
![]() $\log (\varphi _\varsigma (u))$
is well-defined. It will be helpful to have a similar formulation for the iterates
$\log (\varphi _\varsigma (u))$
is well-defined. It will be helpful to have a similar formulation for the iterates
 $$ \begin{align*} (\mathcal L_{z,\rho}^n\varphi)(u) = \sum_{\sigma^n(u')=u} e^{\alpha^{(n)}_z(u')} (\rho(\operatorname{\mathrm{Hol}}^{(n)}(u')) \cdot \varphi(u')), \end{align*} $$
$$ \begin{align*} (\mathcal L_{z,\rho}^n\varphi)(u) = \sum_{\sigma^n(u')=u} e^{\alpha^{(n)}_z(u')} (\rho(\operatorname{\mathrm{Hol}}^{(n)}(u')) \cdot \varphi(u')), \end{align*} $$
with
 $$ \begin{align*} \alpha^{(n)}_z(u) := &\int_0^{\tau^{(n)}(u)} (\varsigma \circ p) (u,s,t) \, dt\\ &- z \cdot \tau^{(n)}(u,s) - \log (\varphi_\varsigma^{(n)}(u)) + \log (\varphi_\varsigma^{(n)}(\sigma(u))) - n\log P(\varsigma) \end{align*} $$
$$ \begin{align*} \alpha^{(n)}_z(u) := &\int_0^{\tau^{(n)}(u)} (\varsigma \circ p) (u,s,t) \, dt\\ &- z \cdot \tau^{(n)}(u,s) - \log (\varphi_\varsigma^{(n)}(u)) + \log (\varphi_\varsigma^{(n)}(\sigma(u))) - n\log P(\varsigma) \end{align*} $$
for all
![]() $u \in U$
. Here, we write
$u \in U$
. Here, we write
 $$ \begin{align*} \varphi_\varsigma^{(n)}(u) := \prod_{i=0}^{n-1} \varphi_\varsigma( \varsigma^i(u) ) \end{align*} $$
$$ \begin{align*} \varphi_\varsigma^{(n)}(u) := \prod_{i=0}^{n-1} \varphi_\varsigma( \varsigma^i(u) ) \end{align*} $$
for the
![]() $n{\textrm {th}}$
ergodic product along
$n{\textrm {th}}$
ergodic product along
![]() $\sigma $
.
$\sigma $
.
Our overarching goal is to establish spectral bounds for these operators; in §5, we ultimately prove the following theorem.
Theorem 3.2. There are constants
![]() $C> 0$
and
$C> 0$
and
![]() $r < 1$
so that
$r < 1$
so that
for all
![]() $\varphi \in C^1(U, V^\rho )$
, all non-trivial irreducible representations
$\varphi \in C^1(U, V^\rho )$
, all non-trivial irreducible representations
![]() $\rho $
of G, and any
$\rho $
of G, and any
![]() $z \in \mathbb {C}$
with
$z \in \mathbb {C}$
with
![]() $|\mathrm {Re}(z) - P(\varsigma )| < 1$
.
$|\mathrm {Re}(z) - P(\varsigma )| < 1$
.
The remainder of this section is devoted to showing how we obtain Theorem A from Theorem 3.2.
Given
![]() $\varphi _0, \ldots , \varphi _k \in C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
with
$\varphi _0, \ldots , \varphi _k \in C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
with
 $\int _{U_{\tau , \operatorname {\mathrm {Hol}}}} \varphi _i \, d\nu ^u \, d\omega \, dr = 0$
, let
$\int _{U_{\tau , \operatorname {\mathrm {Hol}}}} \varphi _i \, d\nu ^u \, d\omega \, dr = 0$
, let
 $$ \begin{align*} \beta_k(t_1, \ldots, t_k) := \int_U \int_0^{\tau(u)} \int_G \varphi_0(u, h, r) \bigg( \prod_{i=1}^k \varphi_i(u, h, r + t_i) \bigg) \, d\omega \, dr \, d\nu^u \end{align*} $$
$$ \begin{align*} \beta_k(t_1, \ldots, t_k) := \int_U \int_0^{\tau(u)} \int_G \varphi_0(u, h, r) \bigg( \prod_{i=1}^k \varphi_i(u, h, r + t_i) \bigg) \, d\omega \, dr \, d\nu^u \end{align*} $$
be the
![]() $k{\textrm {th}}$
correlation function
$k{\textrm {th}}$
correlation function
 $\beta _k \colon \mathbb {R}^k_+ \to \mathbb {R}$
. To show that
$\beta _k \colon \mathbb {R}^k_+ \to \mathbb {R}$
. To show that
![]() $\beta _k$
decays exponentially in
$\beta _k$
decays exponentially in
![]() $t_1, \ldots , t_k$
, we show that the integral defining its Laplace transform
$t_1, \ldots , t_k$
, we show that the integral defining its Laplace transform
![]() $\hat \beta (\xi _1, \ldots , \xi _k)$
converges absolutely for some fixed values of
$\hat \beta (\xi _1, \ldots , \xi _k)$
converges absolutely for some fixed values of
![]() $\xi _1, \ldots , \xi _k$
. The following lemma expresses the Laplace transform in terms of the transfer operators we have just defined, the proof of which consists almost entirely of elementary integral manipulations.
$\xi _1, \ldots , \xi _k$
. The following lemma expresses the Laplace transform in terms of the transfer operators we have just defined, the proof of which consists almost entirely of elementary integral manipulations.
We are somewhat cavalier in interchanging sums and integrals, though this is eventually justified as the final expression we obtain is absolutely convergent.
Lemma 3.3. Given
![]() $\varphi _0, \ldots , \varphi _k \kern1pt{\in}\kern1pt C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
as previously with
$\varphi _0, \ldots , \varphi _k \kern1pt{\in}\kern1pt C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
as previously with
 $\int _{U_{\tau , \operatorname {\mathrm {Hol}}}} \varphi _i \, d\nu ^u\, d\omega \, dr \kern1pt{=} 0$
, we can bound the Laplace transform of the kth-order correlation by
$\int _{U_{\tau , \operatorname {\mathrm {Hol}}}} \varphi _i \, d\nu ^u\, d\omega \, dr \kern1pt{=} 0$
, we can bound the Laplace transform of the kth-order correlation by
 $$ \begin{align*} |\hat\beta_k(\xi_1, \ldots, \xi_k)| \; \leq \sum_\rho \sum_{n_1, \ldots, n_k=1}^\infty \int_U (\mathcal L^{\max n_j}_{\rho, P(\varsigma)+\xi}|\hat\varphi^\rho_{0,-\xi}|)(u) \bigg( \prod_{i=1}^k \|\hat\varphi_{i,\xi_i}\|_{C^0} \bigg) \, d\nu^u \end{align*} $$
$$ \begin{align*} |\hat\beta_k(\xi_1, \ldots, \xi_k)| \; \leq \sum_\rho \sum_{n_1, \ldots, n_k=1}^\infty \int_U (\mathcal L^{\max n_j}_{\rho, P(\varsigma)+\xi}|\hat\varphi^\rho_{0,-\xi}|)(u) \bigg( \prod_{i=1}^k \|\hat\varphi_{i,\xi_i}\|_{C^0} \bigg) \, d\nu^u \end{align*} $$
for
![]() $\mathrm {Re}(\xi _1), \ldots , \mathrm {Re}(\xi _k) < 0$
. Here, we use
$\mathrm {Re}(\xi _1), \ldots , \mathrm {Re}(\xi _k) < 0$
. Here, we use
![]() $\hat \varphi _{i, \xi _i}$
to denote the function
$\hat \varphi _{i, \xi _i}$
to denote the function
 $$ \begin{align*} \hat\varphi_{i,\xi_i}(u, h) := \int_0^{\tau(u)} \varphi_i(u, h, t_i) e^{-\xi_it_i} \, dt_i \end{align*} $$
$$ \begin{align*} \hat\varphi_{i,\xi_i}(u, h) := \int_0^{\tau(u)} \varphi_i(u, h, t_i) e^{-\xi_it_i} \, dt_i \end{align*} $$
and
![]() $\hat \beta _k$
to denote the Laplace transform
$\hat \beta _k$
to denote the Laplace transform
 $$ \begin{align*} \hat \beta_k (\xi_1, \ldots, \xi_k) := \int_0^\infty \cdots \int_0^\infty \beta_k(t_1, \ldots, t_k) e^{-(\xi_1 t_1 + \cdots + \xi_kt_k)} \, dt_1 \, \ldots \, dt_k \end{align*} $$
$$ \begin{align*} \hat \beta_k (\xi_1, \ldots, \xi_k) := \int_0^\infty \cdots \int_0^\infty \beta_k(t_1, \ldots, t_k) e^{-(\xi_1 t_1 + \cdots + \xi_kt_k)} \, dt_1 \, \ldots \, dt_k \end{align*} $$
for
![]() $\xi _i \in \mathbb {R}$
.
$\xi _i \in \mathbb {R}$
.
Proof. By definition, the Laplace transform
![]() $\hat \beta _k(\xi _1, \ldots , \xi _k)$
of
$\hat \beta _k(\xi _1, \ldots , \xi _k)$
of
![]() $\beta _k(t_1, \ldots , t_k)$
is given by
$\beta _k(t_1, \ldots , t_k)$
is given by
 $$ \begin{align} &\int_0^\infty \hspace{-1.5pt} \cdots \hspace{-1.5pt} \int_0^\infty \int_U \int_{\max(0,\tau(u)-t_i)}^{\tau(u)}\int_G \varphi_0(u,h,r)\nonumber\\ &\quad\cdot\bigg( \prod_{i=1}^k \varphi_i(u,h,r+t_i) e^{-\xi_i t_i} \bigg) \, d\omega \, dr \, d\nu^u \, dt_1 \, \cdots \, dt_k \end{align} $$
$$ \begin{align} &\int_0^\infty \hspace{-1.5pt} \cdots \hspace{-1.5pt} \int_0^\infty \int_U \int_{\max(0,\tau(u)-t_i)}^{\tau(u)}\int_G \varphi_0(u,h,r)\nonumber\\ &\quad\cdot\bigg( \prod_{i=1}^k \varphi_i(u,h,r+t_i) e^{-\xi_i t_i} \bigg) \, d\omega \, dr \, d\nu^u \, dt_1 \, \cdots \, dt_k \end{align} $$
for
![]() $\xi _1, \ldots , \xi _k \in \mathbb {C}$
. As the systems of inequalities
$\xi _1, \ldots , \xi _k \in \mathbb {C}$
. As the systems of inequalities

are obviously equivalent, we can rewrite (3.1) as
 $$ \begin{align*} &\int_U \int_G \int_0^{\tau(u)} \int_{\tau(u)}^\infty \cdots \int_{\tau(u)}^\infty \varphi_0(u, h, r)\\ &\quad\cdot\bigg( \prod_{i=1}^k \varphi_i(u, h, t_i)e^{-\xi_i(t_i-r)} \bigg) \, dt_1 \, \cdots \, dt_k \, dr \, d\omega \, d\nu^u \end{align*} $$
$$ \begin{align*} &\int_U \int_G \int_0^{\tau(u)} \int_{\tau(u)}^\infty \cdots \int_{\tau(u)}^\infty \varphi_0(u, h, r)\\ &\quad\cdot\bigg( \prod_{i=1}^k \varphi_i(u, h, t_i)e^{-\xi_i(t_i-r)} \bigg) \, dt_1 \, \cdots \, dt_k \, dr \, d\omega \, d\nu^u \end{align*} $$
by reparametrizing the domain of integration. Let us focus on the k innermost integrals over
![]() $t_1, \ldots , t_k$
, which can be broken up into a sum of integrals
$t_1, \ldots , t_k$
, which can be broken up into a sum of integrals
 $$ \begin{align*} \sum_{n_1, \ldots, n_k = 1}^\infty \int_{\tau^{(n_1)}(u)}^{\tau^{(n_1 + 1)}(u)} \hspace{-18pt} \cdots \int_{\tau^{(n_k)}(u)}^{\tau^{(n_k+1)}(u)} \varphi_0(u, h, r) \bigg( \prod_{i=1}^k \varphi_i(u, h, t_i)e^{-\xi_i(t_i-r)} \bigg) \, dt_1 \, \cdots \, dt_k \end{align*} $$
$$ \begin{align*} \sum_{n_1, \ldots, n_k = 1}^\infty \int_{\tau^{(n_1)}(u)}^{\tau^{(n_1 + 1)}(u)} \hspace{-18pt} \cdots \int_{\tau^{(n_k)}(u)}^{\tau^{(n_k+1)}(u)} \varphi_0(u, h, r) \bigg( \prod_{i=1}^k \varphi_i(u, h, t_i)e^{-\xi_i(t_i-r)} \bigg) \, dt_1 \, \cdots \, dt_k \end{align*} $$
over intervals of the form
![]() $[\tau ^{(n)}(u), \tau ^{(n+1)}(u)]$
. Of course, we can rewrite this as
$[\tau ^{(n)}(u), \tau ^{(n+1)}(u)]$
. Of course, we can rewrite this as
 $$ \begin{align*} &\sum_{n_1, \ldots, n_k = 1}^\infty \int_{0}^{\tau(\sigma^{n_1}(u))} \hspace{-18pt} \cdots \int_{0}^{\tau(\sigma^{n_k}(u))} \bigg[ \varphi_0(u, h, r)\\ &\qquad\cdot \bigg( \prod_{i=1}^k \varphi_i(u, h, t_i + \tau^{(n_i)}(u))e^{-\xi_i(t_i-r + \tau^{(n_i)}(u))} \bigg) \bigg] \, dt_1 \, \cdots \, dt_k \end{align*} $$
$$ \begin{align*} &\sum_{n_1, \ldots, n_k = 1}^\infty \int_{0}^{\tau(\sigma^{n_1}(u))} \hspace{-18pt} \cdots \int_{0}^{\tau(\sigma^{n_k}(u))} \bigg[ \varphi_0(u, h, r)\\ &\qquad\cdot \bigg( \prod_{i=1}^k \varphi_i(u, h, t_i + \tau^{(n_i)}(u))e^{-\xi_i(t_i-r + \tau^{(n_i)}(u))} \bigg) \bigg] \, dt_1 \, \cdots \, dt_k \end{align*} $$
by changing variables, replacing
![]() $t_i$
with
$t_i$
with
![]() $t_i + \tau ^{(n_i)}(u)$
. We can rewrite the integrand here as
$t_i + \tau ^{(n_i)}(u)$
. We can rewrite the integrand here as
 $$ \begin{align} \varphi_0(u, h, r) \bigg( \prod_{i=1}^k\varphi_i( \sigma^{n_i}(u), ( \operatorname{\mathrm{Hol}}^{(n_i)}(u) )^{-1} \circ h, t_i ) e^{-\xi_i(t_i - r + \tau^{(n_i)}(u))} \bigg) \end{align} $$
$$ \begin{align} \varphi_0(u, h, r) \bigg( \prod_{i=1}^k\varphi_i( \sigma^{n_i}(u), ( \operatorname{\mathrm{Hol}}^{(n_i)}(u) )^{-1} \circ h, t_i ) e^{-\xi_i(t_i - r + \tau^{(n_i)}(u))} \bigg) \end{align} $$
using the identifications we made in constructing
![]() $U_{\tau , \operatorname {\mathrm {Hol}}}$
. Evaluating the integral of (3.2) with respect to
$U_{\tau , \operatorname {\mathrm {Hol}}}$
. Evaluating the integral of (3.2) with respect to
![]() $t_1$
through
$t_1$
through
![]() $t_k$
over the intervals
$t_k$
over the intervals
![]() $[0,\tau (\sigma ^{n_1}(u))]$
through
$[0,\tau (\sigma ^{n_1}(u))]$
through
![]() $[0, \tau (\sigma ^{n_k}(u))]$
then yields
$[0, \tau (\sigma ^{n_k}(u))]$
then yields
 $$ \begin{align} \varphi_0(u,h,r) e^{r\xi} \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u), ( \operatorname{\mathrm{Hol}}^{(n_i)}(u) )^{-1} \circ h ) e^{-\xi_i \tau^{(n_i)}(u)} \bigg), \end{align} $$
$$ \begin{align} \varphi_0(u,h,r) e^{r\xi} \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u), ( \operatorname{\mathrm{Hol}}^{(n_i)}(u) )^{-1} \circ h ) e^{-\xi_i \tau^{(n_i)}(u)} \bigg), \end{align} $$
where we set
 $\xi := \displaystyle \smash {\sum _{i=1}^k} \xi _i$
. Similarly, evaluating the integral of (3.3) with respect to r on
$\xi := \displaystyle \smash {\sum _{i=1}^k} \xi _i$
. Similarly, evaluating the integral of (3.3) with respect to r on
![]() $[0, \tau (u)]$
yields
$[0, \tau (u)]$
yields
 $$ \begin{align*} \hat\varphi_{0,-\xi}(u,h) \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u), ( \operatorname{\mathrm{Hol}}^{(n_i)}(u) )^{-1} \circ h ) e^{-\xi_i \tau^{(n_i)}(u)} \bigg) \end{align*} $$
$$ \begin{align*} \hat\varphi_{0,-\xi}(u,h) \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u), ( \operatorname{\mathrm{Hol}}^{(n_i)}(u) )^{-1} \circ h ) e^{-\xi_i \tau^{(n_i)}(u)} \bigg) \end{align*} $$
and so (3.1) becomes
 $$ \begin{align} \sum_{n_1, \ldots, n_k=1}^\infty \int_U \int_G \hat\varphi_{0,-\xi}(u,h) \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u), ( \operatorname{\mathrm{Hol}}^{(n_i)}(u) )^{-1} \circ h ) e^{-\xi_i \tau^{(n_i)}(u)} \bigg) \, d\omega \, d\nu^u \end{align} $$
$$ \begin{align} \sum_{n_1, \ldots, n_k=1}^\infty \int_U \int_G \hat\varphi_{0,-\xi}(u,h) \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u), ( \operatorname{\mathrm{Hol}}^{(n_i)}(u) )^{-1} \circ h ) e^{-\xi_i \tau^{(n_i)}(u)} \bigg) \, d\omega \, d\nu^u \end{align} $$
after interchanging the order of integration and summation.
As
![]() $\omega $
is bi-invariant, we can replace h with
$\omega $
is bi-invariant, we can replace h with
![]() $( \operatorname {\mathrm {Hol}}^{(\max n_j)}(u) ) \circ h$
. Of course, we have the identity
$( \operatorname {\mathrm {Hol}}^{(\max n_j)}(u) ) \circ h$
. Of course, we have the identity
![]() $( \operatorname {\mathrm {Hol}}^{(n_i)}(u) )^{-1} \circ \operatorname {\mathrm {Hol}}^{(\max n_j)}(u) = \operatorname {\mathrm {Hol}}^{(n_i - (\max n_j))}(\sigma ^{n_i}(u))$
, and (3.4) becomes
$( \operatorname {\mathrm {Hol}}^{(n_i)}(u) )^{-1} \circ \operatorname {\mathrm {Hol}}^{(\max n_j)}(u) = \operatorname {\mathrm {Hol}}^{(n_i - (\max n_j))}(\sigma ^{n_i}(u))$
, and (3.4) becomes
 $$ \begin{align*} \sum_{n_1, \ldots, n_k=1}^\infty \int_U \int_G \bigg[ &\hat\varphi_{0,-\xi}(u,\operatorname{\mathrm{Hol}}^{(\max n_j)}(u) \circ h)\\[-3pt] &\cdot \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u), \operatorname{\mathrm{Hol}}^{(n_i - (\max n_j))}(u) \circ h ) e^{-\xi_i \tau^{(n_i)}(u)} \bigg) \bigg] \, d\omega \, d\nu^u \end{align*} $$
$$ \begin{align*} \sum_{n_1, \ldots, n_k=1}^\infty \int_U \int_G \bigg[ &\hat\varphi_{0,-\xi}(u,\operatorname{\mathrm{Hol}}^{(\max n_j)}(u) \circ h)\\[-3pt] &\cdot \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u), \operatorname{\mathrm{Hol}}^{(n_i - (\max n_j))}(u) \circ h ) e^{-\xi_i \tau^{(n_i)}(u)} \bigg) \bigg] \, d\omega \, d\nu^u \end{align*} $$
with this change of variables. This is equivalent to
 $$ \begin{align*} \sum_{n_1, \ldots, n_k = 1}^\infty \int_G \int_U \bigg[ &\hat\varphi_{0,-\xi}(u,\operatorname{\mathrm{Hol}}^{(\max n_j)}(u) \circ h)\\[-3pt] &\cdot \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u), \operatorname{\mathrm{Hol}}^{(n_i - (\max n_j))}(u) \circ h ) e^{-\xi_i \tau^{(n_i)}(u)} \bigg)\bigg] \, d\nu^u \, d\omega \end{align*} $$
$$ \begin{align*} \sum_{n_1, \ldots, n_k = 1}^\infty \int_G \int_U \bigg[ &\hat\varphi_{0,-\xi}(u,\operatorname{\mathrm{Hol}}^{(\max n_j)}(u) \circ h)\\[-3pt] &\cdot \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u), \operatorname{\mathrm{Hol}}^{(n_i - (\max n_j))}(u) \circ h ) e^{-\xi_i \tau^{(n_i)}(u)} \bigg)\bigg] \, d\nu^u \, d\omega \end{align*} $$
by simply reversing the order of integration. Applying
![]() $\mathcal L_{P(\varsigma ),0}$
to the integrand a total of
$\mathcal L_{P(\varsigma ),0}$
to the integrand a total of
![]() $\max n_j$
times yields
$\max n_j$
times yields
 $$ \begin{align*} \sum_{{\sigma^{\max n_j}(u')=u}} \bigg[ &\hat\varphi_{0,-\xi}(u',\operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h)\\ &\cdot \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u'), \operatorname{\mathrm{Hol}}^{(n_i - (\max n_j))}(u') \circ h ) e^{-\xi_i \tau^{(n_i)}(u')} \bigg) e^{\alpha_{P(\varsigma)}^{(\max n_j)}(u')}\bigg] \end{align*} $$
$$ \begin{align*} \sum_{{\sigma^{\max n_j}(u')=u}} \bigg[ &\hat\varphi_{0,-\xi}(u',\operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h)\\ &\cdot \bigg( \prod_{i=1}^k \hat\varphi_{i,\xi_i}( \sigma^{n_i}(u'), \operatorname{\mathrm{Hol}}^{(n_i - (\max n_j))}(u') \circ h ) e^{-\xi_i \tau^{(n_i)}(u')} \bigg) e^{\alpha_{P(\varsigma)}^{(\max n_j)}(u')}\bigg] \end{align*} $$
for any given values of
![]() $n_1, \ldots , n_k \in \mathbb {N}$
. Now, observe that
$n_1, \ldots , n_k \in \mathbb {N}$
. Now, observe that
![]() $e^{-\mathrm {Re}(\xi _i) \tau ^{(n_i)}(u)}$
is at most
$e^{-\mathrm {Re}(\xi _i) \tau ^{(n_i)}(u)}$
is at most
![]() $e^{- \mathrm {Re}(\xi _i) \tau ^{(\max n_j)}(u)}$
so long as each
$e^{- \mathrm {Re}(\xi _i) \tau ^{(\max n_j)}(u)}$
so long as each
![]() $\mathrm {Re}(\xi _i)$
is negative. Hence, we can bound the magnitude of the integrand from above by
$\mathrm {Re}(\xi _i)$
is negative. Hence, we can bound the magnitude of the integrand from above by
 $$ \begin{align*} \sum_{\sigma^{\max n_j}(u')=u} |\hat\varphi_{0,-\xi}(u',\operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h)| \bigg( \prod_{i=1}^k \|\hat\varphi_{i,\xi_i}\|_{C^0} \bigg) e^{-\mathrm{Re}(\xi) \tau^{(\max n_j)}(u') +\alpha_{P(\varsigma)}^{(\max n_j)}(u')} \end{align*} $$
$$ \begin{align*} \sum_{\sigma^{\max n_j}(u')=u} |\hat\varphi_{0,-\xi}(u',\operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h)| \bigg( \prod_{i=1}^k \|\hat\varphi_{i,\xi_i}\|_{C^0} \bigg) e^{-\mathrm{Re}(\xi) \tau^{(\max n_j)}(u') +\alpha_{P(\varsigma)}^{(\max n_j)}(u')} \end{align*} $$
using the triangle inequality. Rearranging this expression, we see that the magnitude of the integrand is bounded above by
 $$ \begin{align} &\bigg( \prod_{i=1}^k \|\hat\varphi_{i,\xi_i}\|_{C^0} \bigg)\nonumber\\ &\quad\cdot\bigg(\sum_{\sigma^{\max n_j}(u')=u} |\hat\varphi_{0,-\xi}(u',\operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h)|e^{-\mathrm{Re}(\xi) \tau^{(\max n_j)}(u') +\alpha_{P(\varsigma)}^{(\max n_j)}(u')} \bigg), \end{align} $$
$$ \begin{align} &\bigg( \prod_{i=1}^k \|\hat\varphi_{i,\xi_i}\|_{C^0} \bigg)\nonumber\\ &\quad\cdot\bigg(\sum_{\sigma^{\max n_j}(u')=u} |\hat\varphi_{0,-\xi}(u',\operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h)|e^{-\mathrm{Re}(\xi) \tau^{(\max n_j)}(u') +\alpha_{P(\varsigma)}^{(\max n_j)}(u')} \bigg), \end{align} $$
which is reminiscent of the expression defining the transfer operator. To make this concrete, recall that we have an
![]() $L^2(G)$
-invariant decomposition of the function
$L^2(G)$
-invariant decomposition of the function
![]() $\hat \varphi _{0,-\xi } \in C^1(U,L^2(G))$
in terms of its isotypic components
$\hat \varphi _{0,-\xi } \in C^1(U,L^2(G))$
in terms of its isotypic components
 $$ \begin{align*} \hat \varphi_{0,-\xi}( u', \operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h ) = \sum_{\rho} \hat \varphi_{0,-\xi}^\rho( u', \operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h ), \end{align*} $$
$$ \begin{align*} \hat \varphi_{0,-\xi}( u', \operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h ) = \sum_{\rho} \hat \varphi_{0,-\xi}^\rho( u', \operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h ), \end{align*} $$
where the sum is taken over irreducible representations
![]() $\rho $
of G, including the trivial representation. Once again, by the triangle inequality, we can bound (3.5) above by
$\rho $
of G, including the trivial representation. Once again, by the triangle inequality, we can bound (3.5) above by
 $$ \begin{align*} &\bigg( \prod_{i=1}^k \|\hat\varphi_{i,\xi_i}\|_{C^0} \bigg)\\ &\quad\cdot\bigg(\sum_\rho \sum_{\sigma^{\max n_j}(u')=u} |\hat\varphi^\rho_{0,-\xi}(u',\operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h)|e^{-\xi \tau^{(\max n_j)}(u') +\alpha_{P(\varsigma)}^{(\max n_j)}(u')} \bigg) \end{align*} $$
$$ \begin{align*} &\bigg( \prod_{i=1}^k \|\hat\varphi_{i,\xi_i}\|_{C^0} \bigg)\\ &\quad\cdot\bigg(\sum_\rho \sum_{\sigma^{\max n_j}(u')=u} |\hat\varphi^\rho_{0,-\xi}(u',\operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h)|e^{-\xi \tau^{(\max n_j)}(u') +\alpha_{P(\varsigma)}^{(\max n_j)}(u')} \bigg) \end{align*} $$
where we quickly recognize the transfer operator
 $\mathcal L_{\rho ,P(\varsigma )+\mathrm {Re}(\xi )}^{\max n_j}$
applied to
$\mathcal L_{\rho ,P(\varsigma )+\mathrm {Re}(\xi )}^{\max n_j}$
applied to
 $|\hat \varphi ^\rho _{0,-\xi } |$
, noting, of course, that
$|\hat \varphi ^\rho _{0,-\xi } |$
, noting, of course, that
 $$ \begin{align*} | \hat \varphi_{0,-\xi}^\rho ( u', \operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h ) | = | \rho( \operatorname{\mathrm{Hol}}^{(\max n_j)}(u') ) \cdot \hat \varphi_{0,-\xi}^\rho ( u', h )| \end{align*} $$
$$ \begin{align*} | \hat \varphi_{0,-\xi}^\rho ( u', \operatorname{\mathrm{Hol}}^{(\max n_j)}(u') \circ h ) | = | \rho( \operatorname{\mathrm{Hol}}^{(\max n_j)}(u') ) \cdot \hat \varphi_{0,-\xi}^\rho ( u', h )| \end{align*} $$
for each
![]() $\rho $
. Putting this back together, we see that (3.1) is bounded above by
$\rho $
. Putting this back together, we see that (3.1) is bounded above by
 $$ \begin{align*} \sum_\rho \sum_{n_1, \ldots, n_k=1}^\infty \int_U \int_G (\mathcal L^{\max n_j}_{\rho, P(\varsigma) + \mathrm{Re}(\xi)}|\hat\varphi^\rho_{0,-\xi}|)(u, h) \bigg( \prod_{i=1}^k \|\hat\varphi_{i,\xi_i}\|_{C^0} \bigg) \, d\omega \, d\nu^u \end{align*} $$
$$ \begin{align*} \sum_\rho \sum_{n_1, \ldots, n_k=1}^\infty \int_U \int_G (\mathcal L^{\max n_j}_{\rho, P(\varsigma) + \mathrm{Re}(\xi)}|\hat\varphi^\rho_{0,-\xi}|)(u, h) \bigg( \prod_{i=1}^k \|\hat\varphi_{i,\xi_i}\|_{C^0} \bigg) \, d\omega \, d\nu^u \end{align*} $$
in magnitude, as desired.
We now simply use the bounds in Theorem 3.2 to conclude that the Laplace transform
![]() $\hat \beta $
in Lemma 3.3 converges.
$\hat \beta $
in Lemma 3.3 converges.
Theorem 3.4. With conditions as above, there are uniform constants
![]() $C> 0$
and
$C> 0$
and
![]() $r < 1$
so that
$r < 1$
so that
 $$ \begin{align*} \bigg| \int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \varphi_0(u,h,r) \bigg( \prod_{i=1}^k \varphi_i(u,h,r+t_i) \bigg) \, d\nu^u \, d\omega \, dr \bigg| \leq C r^{\max t_j} (\|\varphi_0\|_{C^1} \cdot \cdots \cdot \|\varphi_k\|_{C^1}) \end{align*} $$
$$ \begin{align*} \bigg| \int_{U_{\tau, \operatorname{\mathrm{Hol}}}} \varphi_0(u,h,r) \bigg( \prod_{i=1}^k \varphi_i(u,h,r+t_i) \bigg) \, d\nu^u \, d\omega \, dr \bigg| \leq C r^{\max t_j} (\|\varphi_0\|_{C^1} \cdot \cdots \cdot \|\varphi_k\|_{C^1}) \end{align*} $$
for all
![]() $\varphi _0, \ldots , \varphi _k \in C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
with
$\varphi _0, \ldots , \varphi _k \in C^1(U_{\tau , \operatorname {\mathrm {Hol}}}, \mathbb {C})$
with
 $\int _{U_{\tau ,\operatorname {\mathrm {Hol}}}} \varphi _i \, d\nu ^u \, d\omega \, dr = 0$
.
$\int _{U_{\tau ,\operatorname {\mathrm {Hol}}}} \varphi _i \, d\nu ^u \, d\omega \, dr = 0$
.
Proof. We assume that Theorem 3.2 holds, and so we have
for all non-trivial irreducible
![]() $\rho $
, all
$\rho $
, all
![]() $\varphi \in C^1(U, V^\rho )$
and for each
$\varphi \in C^1(U, V^\rho )$
and for each
![]() $z \in \mathbb {C}$
with
$z \in \mathbb {C}$
with
![]() $|\mathrm {Re}(z) - P(\varsigma )| < 1$
. Up to choosing larger values of C and r, we can also assume that the same inequality holds when
$|\mathrm {Re}(z) - P(\varsigma )| < 1$
. Up to choosing larger values of C and r, we can also assume that the same inequality holds when
![]() $\rho $
is trivial: this is precisely the main result of either [Reference Dolgopyat11, Theorem 2] or [Reference Butterley and War9, Proposition 3.16], depending on the regularity hypothesis we are using in Theorem A.
$\rho $
is trivial: this is precisely the main result of either [Reference Dolgopyat11, Theorem 2] or [Reference Butterley and War9, Proposition 3.16], depending on the regularity hypothesis we are using in Theorem A.
We show that the expression bounding
![]() $\hat \beta (\xi _1, \ldots , \xi _k)$
in Lemma 3.3 converges whenever the real parts of
$\hat \beta (\xi _1, \ldots , \xi _k)$
in Lemma 3.3 converges whenever the real parts of
![]() $\xi _i$
simultaneously lie in the interval
$\xi _i$
simultaneously lie in the interval
![]() $-1/k < \mathrm {Re}(\xi _i) < 0$
. The decay desired follows immediately from applying the inverse Laplace transform with the specific bounds we obtain.
$-1/k < \mathrm {Re}(\xi _i) < 0$
. The decay desired follows immediately from applying the inverse Laplace transform with the specific bounds we obtain.
Fix
![]() $\xi _1, \ldots , \xi _k$
with
$\xi _1, \ldots , \xi _k$
with
![]() $-1/k < \mathrm {Re}(\xi _i) < 0$
. As before, we consider the function
$-1/k < \mathrm {Re}(\xi _i) < 0$
. As before, we consider the function
 $$ \begin{align*} \hat \varphi_{i,\xi_i}(u,h) = \int_0^{\tau(u)} \varphi_i(u,h,t) e^{-\xi_it_i} \, dt_i \end{align*} $$
$$ \begin{align*} \hat \varphi_{i,\xi_i}(u,h) = \int_0^{\tau(u)} \varphi_i(u,h,t) e^{-\xi_it_i} \, dt_i \end{align*} $$
and decompose
![]() $\hat \varphi _{0,-\xi }$
into its isotypic components
$\hat \varphi _{0,-\xi }$
into its isotypic components
 $$ \begin{align*} \hat \varphi_{0,-\xi} = \sum_\rho \hat \varphi_{0,-\xi}^\rho, \end{align*} $$
$$ \begin{align*} \hat \varphi_{0,-\xi} = \sum_\rho \hat \varphi_{0,-\xi}^\rho, \end{align*} $$
where
![]() $\xi = \xi _1 + \cdots + \xi _k$
as before, noting that the decomposition of
$\xi = \xi _1 + \cdots + \xi _k$
as before, noting that the decomposition of
![]() $L^2(G)$
into irreducible subspaces commutes with the Laplace transform. By (3.6), whenever
$L^2(G)$
into irreducible subspaces commutes with the Laplace transform. By (3.6), whenever
![]() $- ( 1/ k) < \mathrm {Re}(\xi _i) < 0$
, we have
$- ( 1/ k) < \mathrm {Re}(\xi _i) < 0$
, we have
 $$ \begin{align*} \int_U \int_G ( \mathcal L^{\max n_j}_{\rho,P(\varsigma) + \mathrm{Re}(\xi)} | \hat \varphi^\rho_{0,-\xi} | )(u,h) \, d\omega \, d\nu^u &\leq \| (\mathcal L^{\max n_j}_{\rho, P(\varsigma) + \mathrm{Re}(\xi)} |\hat \varphi^\rho_{0,-\xi} |)\|_{L^2(\nu^u)}\\ &\leq C \|\hat \varphi_{0,-\xi}^\rho\|_{C^1} r^{\max n_j} \end{align*} $$
$$ \begin{align*} \int_U \int_G ( \mathcal L^{\max n_j}_{\rho,P(\varsigma) + \mathrm{Re}(\xi)} | \hat \varphi^\rho_{0,-\xi} | )(u,h) \, d\omega \, d\nu^u &\leq \| (\mathcal L^{\max n_j}_{\rho, P(\varsigma) + \mathrm{Re}(\xi)} |\hat \varphi^\rho_{0,-\xi} |)\|_{L^2(\nu^u)}\\ &\leq C \|\hat \varphi_{0,-\xi}^\rho\|_{C^1} r^{\max n_j} \end{align*} $$
for each
![]() $\rho $
. Combining this with Lemma 3.3, we are reduced to ensuring that
$\rho $
. Combining this with Lemma 3.3, we are reduced to ensuring that
 $$ \begin{align} &\sum_\rho \sum_{n_1, \ldots, n_k = 1}^\infty C \|\hat \varphi^\rho_{0,-\xi} \|_{C^1} r^{\max n_j} \bigg( \prod_{i=1}^k \| \hat \varphi_{i,\xi_i} \|_{C^0} \bigg)\nonumber\\ &\quad< \sum_\rho \sum_{n=1}^\infty k!n^{k-1}C \|\hat \varphi^\rho_{0,-\xi} \|_{C^1} r^n \bigg( \prod_{i=1}^k \|\hat \varphi_{i,\xi_i} \|_{C^0} \bigg) \end{align} $$
$$ \begin{align} &\sum_\rho \sum_{n_1, \ldots, n_k = 1}^\infty C \|\hat \varphi^\rho_{0,-\xi} \|_{C^1} r^{\max n_j} \bigg( \prod_{i=1}^k \| \hat \varphi_{i,\xi_i} \|_{C^0} \bigg)\nonumber\\ &\quad< \sum_\rho \sum_{n=1}^\infty k!n^{k-1}C \|\hat \varphi^\rho_{0,-\xi} \|_{C^1} r^n \bigg( \prod_{i=1}^k \|\hat \varphi_{i,\xi_i} \|_{C^0} \bigg) \end{align} $$
converges. Although this appears promising, note that we can only bound
 $$ \begin{align*} \| \hat \varphi_{0,-\xi}^\rho \|_{C^1} \leq D \|\rho\| \big( \sup_{u \in U} \|\hat \varphi_{0,-\xi}^\rho (u, \cdot)\|_{L^2(G)} \big) \end{align*} $$
$$ \begin{align*} \| \hat \varphi_{0,-\xi}^\rho \|_{C^1} \leq D \|\rho\| \big( \sup_{u \in U} \|\hat \varphi_{0,-\xi}^\rho (u, \cdot)\|_{L^2(G)} \big) \end{align*} $$
for some constant
![]() $D> 0$
. To salvage this, we assume for the moment that we have chosen
$D> 0$
. To salvage this, we assume for the moment that we have chosen
 $\varphi _0 \in C^{2N'}(U_{\tau ,\operatorname {\mathrm {Hol}}},\mathbb {R})$
for a sufficiently large
$\varphi _0 \in C^{2N'}(U_{\tau ,\operatorname {\mathrm {Hol}}},\mathbb {R})$
for a sufficiently large
![]() $N'> 0$
so that we can invoke Theorem 2.11 to bound
$N'> 0$
so that we can invoke Theorem 2.11 to bound
 $$ \begin{align*} \|\rho\|\|\hat \varphi^\rho_{0,-\xi}(u,\cdot) \|_{L^2(G)} \leq \frac {D' \| \hat \varphi_{0,-\xi} (u,\cdot) \|_{C^{N'}}}{\|\rho\|^N} \end{align*} $$
$$ \begin{align*} \|\rho\|\|\hat \varphi^\rho_{0,-\xi}(u,\cdot) \|_{L^2(G)} \leq \frac {D' \| \hat \varphi_{0,-\xi} (u,\cdot) \|_{C^{N'}}}{\|\rho\|^N} \end{align*} $$
pointwise with a fixed constant
![]() $D'> 0$
, where
$D'> 0$
, where
![]() $N> 0$
is the constant guaranteed by Proposition 2.10. With this, it is clear that the expression on the right-hand side of (3.7) converges absolutely, which says immediately that
$N> 0$
is the constant guaranteed by Proposition 2.10. With this, it is clear that the expression on the right-hand side of (3.7) converges absolutely, which says immediately that
![]() $\beta _k$
must decay exponentially fast in
$\beta _k$
must decay exponentially fast in
![]() $t_1, \ldots , t_k$
; this is almost what we wanted to show, but we need an explicit bound on
$t_1, \ldots , t_k$
; this is almost what we wanted to show, but we need an explicit bound on
![]() $\hat \beta _k$
to obtain uniform estimates with the desired constants.
$\hat \beta _k$
to obtain uniform estimates with the desired constants.
Integrating the defining expression for
![]() $\hat \varphi _{i,\xi _i} (u,h)$
by parts, we have
$\hat \varphi _{i,\xi _i} (u,h)$
by parts, we have
 $$ \begin{align*} \hat \varphi_{i, \xi_i}(u,h) =\frac{\varphi_i(u,h,t_i) e^{-\xi_it_i}}{-\xi_i} \bigg|_0^{\tau(u)} + \frac 1 {\xi_i} \int_0^{\tau(u)} \bigg(\frac{\partial}{\partial t_i} \varphi_i (u,h,t_i)\bigg) e^{-\xi_i t_i} \, dt_i \end{align*} $$
$$ \begin{align*} \hat \varphi_{i, \xi_i}(u,h) =\frac{\varphi_i(u,h,t_i) e^{-\xi_it_i}}{-\xi_i} \bigg|_0^{\tau(u)} + \frac 1 {\xi_i} \int_0^{\tau(u)} \bigg(\frac{\partial}{\partial t_i} \varphi_i (u,h,t_i)\bigg) e^{-\xi_i t_i} \, dt_i \end{align*} $$
for each u and h. Assuming that we choose
![]() $\varphi _i \in C^2(U_{\tau ,\operatorname {\mathrm {Hol}}},\mathbb {R})$
, we can crudely bound
$\varphi _i \in C^2(U_{\tau ,\operatorname {\mathrm {Hol}}},\mathbb {R})$
, we can crudely bound
 $$ \begin{align*} \| \hat \varphi_{i, \xi_i} \|_{C^1} \leq \frac{D'' \|\varphi_i\|_{C^2}}{1 + |\mathrm{Im}(\xi_i)|} \end{align*} $$
$$ \begin{align*} \| \hat \varphi_{i, \xi_i} \|_{C^1} \leq \frac{D'' \|\varphi_i\|_{C^2}}{1 + |\mathrm{Im}(\xi_i)|} \end{align*} $$
for some constant
![]() $D''$
that depends only on
$D''$
that depends only on
![]() $\|\tau \|_{C^1}$
; note that it is essential here that
$\|\tau \|_{C^1}$
; note that it is essential here that
![]() $\mathrm {Re}(\xi _i)$
is confined to a bounded interval. We can similarly bound
$\mathrm {Re}(\xi _i)$
is confined to a bounded interval. We can similarly bound
 $$ \begin{align*} \| \hat \varphi_{0, -\xi} \|_{C^{N'}} \leq \frac{D'' \|\varphi_0\|_{C^{N'+1}}}{1 + |\mathrm{Im}(\xi)|} \end{align*} $$
$$ \begin{align*} \| \hat \varphi_{0, -\xi} \|_{C^{N'}} \leq \frac{D'' \|\varphi_0\|_{C^{N'+1}}}{1 + |\mathrm{Im}(\xi)|} \end{align*} $$
by choosing a larger value for
![]() $D''$
if necessary. Putting this all together, we have
$D''$
if necessary. Putting this all together, we have

for all
![]() $\xi _i \in \mathbb {C}$
with
$\xi _i \in \mathbb {C}$
with
![]() $-1/k < \mathrm {Re}(\xi _i) < 0$
. Now, we simply take the inverse Laplace transform in the variables
$-1/k < \mathrm {Re}(\xi _i) < 0$
. Now, we simply take the inverse Laplace transform in the variables
![]() $\xi _1$
through
$\xi _1$
through
![]() $\xi _k$
in succession to obtain
$\xi _k$
in succession to obtain
 $$ \begin{align*} &|\beta_k(t_1, \ldots, t_k)|\\ &\quad\leq \frac {e^{\mathrm{Re}(\xi_1)t_1+ \cdots + \mathrm{Re}(\xi_k) t_k}}{(2\pi)^k} \hspace{-1pt}\int_{-\infty}^\infty \hspace{-1.5pt}\cdots\hspace{-1.5pt} \int_{-\infty}^\infty \frac {\|\varphi_0\|_{C^{N'+1}}} {1 + |s_1 + \cdots + s_k|} \bigg( \prod_{i=1}^k \frac {\|\varphi_i\|_{C^2}} {1+|s_i|} \bigg)\, ds_1 \, \ldots \, ds_k, \end{align*} $$
$$ \begin{align*} &|\beta_k(t_1, \ldots, t_k)|\\ &\quad\leq \frac {e^{\mathrm{Re}(\xi_1)t_1+ \cdots + \mathrm{Re}(\xi_k) t_k}}{(2\pi)^k} \hspace{-1pt}\int_{-\infty}^\infty \hspace{-1.5pt}\cdots\hspace{-1.5pt} \int_{-\infty}^\infty \frac {\|\varphi_0\|_{C^{N'+1}}} {1 + |s_1 + \cdots + s_k|} \bigg( \prod_{i=1}^k \frac {\|\varphi_i\|_{C^2}} {1+|s_i|} \bigg)\, ds_1 \, \ldots \, ds_k, \end{align*} $$
where
![]() $s_i$
is to be interpreted as the imaginary part of
$s_i$
is to be interpreted as the imaginary part of
![]() $\xi _i$
. To complete our decay estimate, we simply need to show that the integral
$\xi _i$
. To complete our decay estimate, we simply need to show that the integral
 $$ \begin{align*} \int_{-\infty}^\infty \cdots \int_{-\infty}^\infty \frac 1 {1 + |s_1 + \cdots + s_k|} \bigg( \prod_{i=1}^k \frac 1 {1 + |s_i|} \bigg) \, ds_1 \, \ldots \, ds_k \end{align*} $$
$$ \begin{align*} \int_{-\infty}^\infty \cdots \int_{-\infty}^\infty \frac 1 {1 + |s_1 + \cdots + s_k|} \bigg( \prod_{i=1}^k \frac 1 {1 + |s_i|} \bigg) \, ds_1 \, \ldots \, ds_k \end{align*} $$
converges. Once the convergence of this integral has been established, we will have shown that
 $$ \begin{align*} |\beta_k(t_1, \ldots, t_k)| < Cr^{\max t_j} \|\varphi_0\|_{C^{N'+1}} \bigg( \prod_{i=1}^k \|\varphi_i\|_{C^2}\bigg) \end{align*} $$
$$ \begin{align*} |\beta_k(t_1, \ldots, t_k)| < Cr^{\max t_j} \|\varphi_0\|_{C^{N'+1}} \bigg( \prod_{i=1}^k \|\varphi_i\|_{C^2}\bigg) \end{align*} $$
for all
 $\varphi _0 \in C^{N'+1}(U_{\tau ,\operatorname {\mathrm {Hol}}}, \mathbb {R})$
and
$\varphi _0 \in C^{N'+1}(U_{\tau ,\operatorname {\mathrm {Hol}}}, \mathbb {R})$
and
![]() $\varphi _i \in C^2(U_{\tau ,\operatorname {\mathrm {Hol}}},\mathbb {R})$
. An identical argument to that given in Lemma 2.1 extends this to
$\varphi _i \in C^2(U_{\tau ,\operatorname {\mathrm {Hol}}},\mathbb {R})$
. An identical argument to that given in Lemma 2.1 extends this to
![]() $C^1$
functions, using [Reference Gorodnik and Spatzier13, Lemma 2.4] once again.
$C^1$
functions, using [Reference Gorodnik and Spatzier13, Lemma 2.4] once again.
We now indicate how to establish the convergence of the integral encountered in the preceding proof.
Lemma 3.5. The integral
 $$ \begin{align*} \int_{-\infty}^\infty \cdots \int_{-\infty}^\infty \frac 1 {1+|s_1 + \cdots + s_k|} \bigg( \prod_{i=1}^k \frac 1 {1+|s_i|} \bigg) \, ds_1 \, \ldots \, ds_k \end{align*} $$
$$ \begin{align*} \int_{-\infty}^\infty \cdots \int_{-\infty}^\infty \frac 1 {1+|s_1 + \cdots + s_k|} \bigg( \prod_{i=1}^k \frac 1 {1+|s_i|} \bigg) \, ds_1 \, \ldots \, ds_k \end{align*} $$
converges.
Proof. We show, in fact, that the function defined by the integral
 $$ \begin{align} f(x) := \int_{-\infty}^\infty \frac 1 {(1+|x+y|)^{0.5-\epsilon}} \bigg( \frac 1 {1 + |y|} \bigg) \, dy \end{align} $$
$$ \begin{align} f(x) := \int_{-\infty}^\infty \frac 1 {(1+|x+y|)^{0.5-\epsilon}} \bigg( \frac 1 {1 + |y|} \bigg) \, dy \end{align} $$
decays at a rate of
 $$ \begin{align*} |f(x)| \leq \frac C {(1 + |x|)^{0.5-2\epsilon}} \end{align*} $$
$$ \begin{align*} |f(x)| \leq \frac C {(1 + |x|)^{0.5-2\epsilon}} \end{align*} $$
for all sufficiently small
![]() $\epsilon> 0$
; the statement of the lemma follows immediately by direct successive integration. We work in the case when
$\epsilon> 0$
; the statement of the lemma follows immediately by direct successive integration. We work in the case when
![]() $x> 0$
, and split the domain of integration in (3.8) into regions where
$x> 0$
, and split the domain of integration in (3.8) into regions where
![]() $x+y, y < 0$
, where
$x+y, y < 0$
, where
![]() $x + y> 0$
but
$x + y> 0$
but
![]() $y < 0$
and where
$y < 0$
and where
![]() $x + y, y> 0$
. In the first case, where
$x + y, y> 0$
. In the first case, where
![]() $x + y$
and y are both negative, we evaluate
$x + y$
and y are both negative, we evaluate
 $$ \begin{align*} \int_{-\infty}^{-x} \frac 1 {(1 - (x+y))^{0.5-\epsilon}} \bigg( \frac 1 {1 - y} \bigg) \, dy \end{align*} $$
$$ \begin{align*} \int_{-\infty}^{-x} \frac 1 {(1 - (x+y))^{0.5-\epsilon}} \bigg( \frac 1 {1 - y} \bigg) \, dy \end{align*} $$
for a fixed
![]() $x> 0$
. One can verify that the antiderivative of this expression is given by
$x> 0$
. One can verify that the antiderivative of this expression is given by
 $$ \begin{align*} \frac {(({1-(x+y)})/({1-y}))^{0.5-\epsilon} {}_2F_1(0.5-\epsilon,0.5-\epsilon;1.5-\epsilon;{x}/({1-y}))}{(0.5-\epsilon) (1-(x+y))^{0.5-\epsilon}} \end{align*} $$
$$ \begin{align*} \frac {(({1-(x+y)})/({1-y}))^{0.5-\epsilon} {}_2F_1(0.5-\epsilon,0.5-\epsilon;1.5-\epsilon;{x}/({1-y}))}{(0.5-\epsilon) (1-(x+y))^{0.5-\epsilon}} \end{align*} $$
where
![]() ${}_2F_1(\cdot ,\cdot ;\cdot ;\cdot )$
is the principal branch of the analytic continuation of the Gaussian hypergeometric function. Hence, the integral evaluates to
${}_2F_1(\cdot ,\cdot ;\cdot ;\cdot )$
is the principal branch of the analytic continuation of the Gaussian hypergeometric function. Hence, the integral evaluates to
 $$ \begin{align*} \int_{-\infty}^{-x} \frac 1 {(1 - (x+y))^{0.5-\epsilon}} \bigg( \frac 1 {1 - y} \bigg) \, dy = \frac {{}_2F_1(0.5-\epsilon,0.5-\epsilon;1.5-\epsilon;{x}/({1+x}))}{(0.5-\epsilon)(1+x)^{0.5-\epsilon}}, \end{align*} $$
$$ \begin{align*} \int_{-\infty}^{-x} \frac 1 {(1 - (x+y))^{0.5-\epsilon}} \bigg( \frac 1 {1 - y} \bigg) \, dy = \frac {{}_2F_1(0.5-\epsilon,0.5-\epsilon;1.5-\epsilon;{x}/({1+x}))}{(0.5-\epsilon)(1+x)^{0.5-\epsilon}}, \end{align*} $$
which can be bounded above by
![]() $C/{(1+x)^{0.5-\epsilon }}$
for an appropriate choice of constant
$C/{(1+x)^{0.5-\epsilon }}$
for an appropriate choice of constant
![]() $C> 0$
, because by [Reference Abramowitz and Stegun1, 15.1.1] the defining series for
$C> 0$
, because by [Reference Abramowitz and Stegun1, 15.1.1] the defining series for
![]() ${}_2F_1(a,b;c;z)$
converges on the unit disc in the complex plane when
${}_2F_1(a,b;c;z)$
converges on the unit disc in the complex plane when
![]() $c - (a+b)> 0$
. Similarly, on the region where
$c - (a+b)> 0$
. Similarly, on the region where
![]() $x+y$
is positive and y is negative, we evaluate
$x+y$
is positive and y is negative, we evaluate
 $$ \begin{align*} &\int_{-x}^0 \frac 1 {(1 + (x+y))^{0.5-\epsilon}} \bigg( \frac 1 {1 - y} \bigg) \, dy\\[4pt] &\quad= \bigg( \frac{(1+(x+y))^{0.5+\epsilon} {}_2F_1(0.5+\epsilon,1;1.5+\epsilon;({1+(x+y)})/({2+x})}{(0.5+\epsilon)(2+x)} \bigg)\bigg|_{y=-x}^{y=0}\\ &\quad= \frac{(1+x)^{0.5+\epsilon} {}_2F_1(0.5+\epsilon,1;1.5+\epsilon;({1+x})/({2+x}))}{(0.5+\epsilon)(2+x)}\\[4pt] &\qquad- \frac{{}_2F_1 (0.5+\epsilon,1;1.5+\epsilon; 1 /({2+x}))}{(0.5+\epsilon)(2+x)}, \end{align*} $$
$$ \begin{align*} &\int_{-x}^0 \frac 1 {(1 + (x+y))^{0.5-\epsilon}} \bigg( \frac 1 {1 - y} \bigg) \, dy\\[4pt] &\quad= \bigg( \frac{(1+(x+y))^{0.5+\epsilon} {}_2F_1(0.5+\epsilon,1;1.5+\epsilon;({1+(x+y)})/({2+x})}{(0.5+\epsilon)(2+x)} \bigg)\bigg|_{y=-x}^{y=0}\\ &\quad= \frac{(1+x)^{0.5+\epsilon} {}_2F_1(0.5+\epsilon,1;1.5+\epsilon;({1+x})/({2+x}))}{(0.5+\epsilon)(2+x)}\\[4pt] &\qquad- \frac{{}_2F_1 (0.5+\epsilon,1;1.5+\epsilon; 1 /({2+x}))}{(0.5+\epsilon)(2+x)}, \end{align*} $$
which can once again be bounded above by
![]() $ C /{(1+x)^{0.5-\epsilon }}$
for the same reasons, though with a possibly larger choice of
$ C /{(1+x)^{0.5-\epsilon }}$
for the same reasons, though with a possibly larger choice of
![]() $C> 0$
. Finally, when both
$C> 0$
. Finally, when both
![]() $x+y$
and y are positive, we evaluate
$x+y$
and y are positive, we evaluate
 $$ \begin{align*} &\int_0^\infty \frac 1 {(1+(x+y))^{0.5-\epsilon}} \bigg( \frac 1 {1+y} \bigg) \, dy\\[4pt] &\quad= \bigg( \frac{( ( {1+(x+y)})/({1+y}) )^{0.5-\epsilon} {}_2F_1(0.5-\epsilon,0.5-\epsilon;1.5-\epsilon;{-x}/({1+y}))}{(0.5-\epsilon)(1+(x+y))^{0.5-\epsilon}} \bigg)\bigg|_{y=0}^{y=\infty}\\[4pt] &\quad= -\frac{{}_2F_1(0.5-\epsilon,0.5-\epsilon;1.5-\epsilon;-x)}{0.5-\epsilon} \end{align*} $$
$$ \begin{align*} &\int_0^\infty \frac 1 {(1+(x+y))^{0.5-\epsilon}} \bigg( \frac 1 {1+y} \bigg) \, dy\\[4pt] &\quad= \bigg( \frac{( ( {1+(x+y)})/({1+y}) )^{0.5-\epsilon} {}_2F_1(0.5-\epsilon,0.5-\epsilon;1.5-\epsilon;{-x}/({1+y}))}{(0.5-\epsilon)(1+(x+y))^{0.5-\epsilon}} \bigg)\bigg|_{y=0}^{y=\infty}\\[4pt] &\quad= -\frac{{}_2F_1(0.5-\epsilon,0.5-\epsilon;1.5-\epsilon;-x)}{0.5-\epsilon} \end{align*} $$
and we simply need to understand the asymptotics of
![]() ${}_2F_1(0.5-\epsilon ,0.5-\epsilon ;1.5-\epsilon ;-x)$
as
${}_2F_1(0.5-\epsilon ,0.5-\epsilon ;1.5-\epsilon ;-x)$
as
![]() $x \to \infty $
. By [Reference Abramowitz and Stegun1, 15.3.1], we have an integral representation given by
$x \to \infty $
. By [Reference Abramowitz and Stegun1, 15.3.1], we have an integral representation given by
 $$ \begin{align} {}_2F_1 (0.5 - \epsilon, 0.5-\epsilon; 1.5-\epsilon;-x) = \frac{\Gamma(1.5-\epsilon)}{\Gamma(0.5-\epsilon)\Gamma(1)} \int_0^1 \frac 1 {t^{0.5+\epsilon}(1+tx)^{0.5-\epsilon}} \, dt \end{align} $$
$$ \begin{align} {}_2F_1 (0.5 - \epsilon, 0.5-\epsilon; 1.5-\epsilon;-x) = \frac{\Gamma(1.5-\epsilon)}{\Gamma(0.5-\epsilon)\Gamma(1)} \int_0^1 \frac 1 {t^{0.5+\epsilon}(1+tx)^{0.5-\epsilon}} \, dt \end{align} $$
for
![]() $x> 1$
. Setting
$x> 1$
. Setting
![]() $u = tx$
, we can rewrite
$u = tx$
, we can rewrite
 $$ \begin{align*} &\int_0^1 \frac 1 {t^{0.5+\epsilon}(1+tx)^{0.5-\epsilon}} \, dt\\[3pt] &\quad= \frac 1 {x^{0.5-\epsilon}} \int_0^x \frac 1 {u^{0.5+\epsilon}(1+u)^{0.5-\epsilon}} \, du\\[3pt] &\quad= \frac 1 {x^{0.5-\epsilon}} \bigg( \int_0^1 \frac 1 {u^{0.5+\epsilon}(1+u)^{0.5-\epsilon}} \, du + \int_1^x \frac 1 {u^{0.5+\epsilon}(1+u)^{0.5-\epsilon}} \, du \bigg), \end{align*} $$
$$ \begin{align*} &\int_0^1 \frac 1 {t^{0.5+\epsilon}(1+tx)^{0.5-\epsilon}} \, dt\\[3pt] &\quad= \frac 1 {x^{0.5-\epsilon}} \int_0^x \frac 1 {u^{0.5+\epsilon}(1+u)^{0.5-\epsilon}} \, du\\[3pt] &\quad= \frac 1 {x^{0.5-\epsilon}} \bigg( \int_0^1 \frac 1 {u^{0.5+\epsilon}(1+u)^{0.5-\epsilon}} \, du + \int_1^x \frac 1 {u^{0.5+\epsilon}(1+u)^{0.5-\epsilon}} \, du \bigg), \end{align*} $$
at which point we note that the expression in parentheses can be bounded above by
![]() $C (1 + \log x)$
. Hence, (3.9) can be bounded above by
$C (1 + \log x)$
. Hence, (3.9) can be bounded above by
![]() $ C/{(1+x)^{0.5 - 2\epsilon }}$
with a possibly larger choice of C, as desired. The proof in the case when
$ C/{(1+x)^{0.5 - 2\epsilon }}$
with a possibly larger choice of C, as desired. The proof in the case when
![]() $x < 0$
is identical.
$x < 0$
is identical.
4 Uniform local non-integrability estimates
In this section, we use the local accessibility of
![]() $f_t$
to establish the uniform local non-integrability estimates necessary to prove Theorem 3.2, drawing on techniques introduced by Dolgopyat in [Reference Dolgopyat12] for group extensions of expanding maps. These arguments require some additional care to adapt to our setting, the principal difficulty being the non-triviality of the fibre bundle
$f_t$
to establish the uniform local non-integrability estimates necessary to prove Theorem 3.2, drawing on techniques introduced by Dolgopyat in [Reference Dolgopyat12] for group extensions of expanding maps. These arguments require some additional care to adapt to our setting, the principal difficulty being the non-triviality of the fibre bundle
![]() $\pi \colon M \to N$
which requires us to choose trivializations to construct the infinitesimal transitivity group as in [Reference Dolgopyat12].
$\pi \colon M \to N$
which requires us to choose trivializations to construct the infinitesimal transitivity group as in [Reference Dolgopyat12].
We want to translate the local accessibility of
![]() $f_t$
into an infinitesimal statement on the Markov model we constructed in §2; we accomplish this in two main steps. The first step is to define a subalgebra of the Lie algebra
$f_t$
into an infinitesimal statement on the Markov model we constructed in §2; we accomplish this in two main steps. The first step is to define a subalgebra of the Lie algebra
![]() $\mathfrak g$
of G that measures the ‘non-integrability’ of the fibre bundle over the weak stable and strong unstable foliations; this can be accomplished before making any reference to our symbolic model. The second step is to translate this into the symbolic model.
$\mathfrak g$
of G that measures the ‘non-integrability’ of the fibre bundle over the weak stable and strong unstable foliations; this can be accomplished before making any reference to our symbolic model. The second step is to translate this into the symbolic model.
For most of what follows, we need to be careful to specify which chart
![]() $V_*$
of the trivialization we are working with at any given point. This is a necessary complication to many of our arguments, because many of the objects we are working with are highly sensitive to the choice of trivialization. Fortunately, however, this will also afford us with the flexibility later on to work with trivializations that are specially adapted to our needs.
$V_*$
of the trivialization we are working with at any given point. This is a necessary complication to many of our arguments, because many of the objects we are working with are highly sensitive to the choice of trivialization. Fortunately, however, this will also afford us with the flexibility later on to work with trivializations that are specially adapted to our needs.
To start, we want to measure and relate three different holonomies associated with
![]() $f_t$
: namely, the holonomies induced by the leaves of the strong stable foliation, the leaves of the strong unstable foliation and the flow.
$f_t$
: namely, the holonomies induced by the leaves of the strong stable foliation, the leaves of the strong unstable foliation and the flow.
Definition 4.1. Fix
![]() $x,y \in N$
with
$x,y \in N$
with
![]() $y \in W^{su}_{g_t}(x)$
, along with trivializations
$y \in W^{su}_{g_t}(x)$
, along with trivializations
![]() $\phi _{x}, \phi _{y}$
of
$\phi _{x}, \phi _{y}$
of
![]() $\pi \colon M \to N$
at x and y corresponding to subsets
$\pi \colon M \to N$
at x and y corresponding to subsets
![]() $V_x, V_y \subset N$
, respectively. We define the unstable holonomy
$V_x, V_y \subset N$
, respectively. We define the unstable holonomy
 $$ \begin{align*} \Theta_{V_x,V_y}^+(x,y)\colon F \to F \end{align*} $$
$$ \begin{align*} \Theta_{V_x,V_y}^+(x,y)\colon F \to F \end{align*} $$
between x and y to be the isometry induced by the map
![]() $\pi ^{-1}(x) \to \pi ^{-1}(y)$
that takes
$\pi ^{-1}(x) \to \pi ^{-1}(y)$
that takes
![]() $a \in \pi ^{-1}(x)$
to the (necessarily unique) point
$a \in \pi ^{-1}(x)$
to the (necessarily unique) point
 $b \in \pi ^{-1}(y) \cap W^{su}_{f_t}(a)$
. The identifications of
$b \in \pi ^{-1}(y) \cap W^{su}_{f_t}(a)$
. The identifications of
![]() $\pi ^{-1}(x)$
and
$\pi ^{-1}(x)$
and
![]() $\pi ^{-1}(y)$
with F are obtained via the trivializations
$\pi ^{-1}(y)$
with F are obtained via the trivializations
![]() $\phi _x, \phi _y$
. The stable holonomy
$\phi _x, \phi _y$
. The stable holonomy
 $\Theta ^-_{V_x,V_y}(x,y)$
is defined analogously for
$\Theta ^-_{V_x,V_y}(x,y)$
is defined analogously for
![]() $y \in W^{ss}_{g_t}(x)$
.
$y \in W^{ss}_{g_t}(x)$
.
Definition 4.2. Fix
![]() $x,y \in N$
with
$x,y \in N$
with
![]() $g_t(x) = y$
, along with trivializations
$g_t(x) = y$
, along with trivializations
![]() $\phi _x,\phi _y$
of
$\phi _x,\phi _y$
of
![]() $\pi \colon M \to N$
at x and y corresponding to subsets
$\pi \colon M \to N$
at x and y corresponding to subsets
![]() $V_x,V_y \subset N$
, respectively. We define the temporal holonomy
$V_x,V_y \subset N$
, respectively. We define the temporal holonomy
 $$ \begin{align*} \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_y}(x,y,t) \colon F \to F \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_y}(x,y,t) \colon F \to F \end{align*} $$
between x and y to be the isometry induced by the map
![]() $\pi ^{-1}(x) \to \pi ^{-1}(y)$
that takes
$\pi ^{-1}(x) \to \pi ^{-1}(y)$
that takes
![]() $a \in \pi ^{-1}(x)$
to
$a \in \pi ^{-1}(x)$
to
![]() $f_t(a) \in \pi ^{-1}(y)$
. The identifications of
$f_t(a) \in \pi ^{-1}(y)$
. The identifications of
![]() $\pi ^{-1}(x)$
and
$\pi ^{-1}(x)$
and
![]() $\pi ^{-1}(y)$
with F are obtained via the trivializations
$\pi ^{-1}(y)$
with F are obtained via the trivializations
![]() $\phi _x, \phi _y$
.
$\phi _x, \phi _y$
.
By the end of this section, we only need to work with a fixed, finite collection of trivializations that cover N. At this stage, however, the flexibility in these definitions is crucial. Our first observation is that the unstable holonomy can be expressed in terms of the temporal holonomies induced by the flow; this is made precise in the following proposition, the proof of which is largely summarized in Figure 1.

Figure 1 Measuring the unstable holonomy between x and y along a sequence of times
![]() $0> t_1 > t_2 > \ldots $
with respect to trivializations
$0> t_1 > t_2 > \ldots $
with respect to trivializations
![]() $(\phi _{n,x})$
and
$(\phi _{n,x})$
and
![]() $(\phi _{n,y})$
defined over charts
$(\phi _{n,y})$
defined over charts
![]() $V_{n}$
, illustrated in the case when the trivializations for x and y coincide. As the unstable leaf through x and y contracts under
$V_{n}$
, illustrated in the case when the trivializations for x and y coincide. As the unstable leaf through x and y contracts under
![]() $g_{t_n}$
, the remaining contribution to the unstable holonomy decreases.
$g_{t_n}$
, the remaining contribution to the unstable holonomy decreases.
Proposition 4.1. Fix
![]() $x, y \in N$
with
$x, y \in N$
with
![]() $y \in W^{su}_{g_t}(x)$
, along with trivializations
$y \in W^{su}_{g_t}(x)$
, along with trivializations
![]() $\phi _{0,x}$
and
$\phi _{0,x}$
and
![]() $\phi _{0,y}$
defined at x and y, respectively. Let
$\phi _{0,y}$
defined at x and y, respectively. Let
![]() $T = (t_n)$
be a monotonic sequence of times with
$T = (t_n)$
be a monotonic sequence of times with
![]() $t_n = 0$
and
$t_n = 0$
and
![]() $t_n \to -\infty $
, and let
$t_n \to -\infty $
, and let
![]() $I_x = (\phi _{n,x})$
and
$I_x = (\phi _{n,x})$
and
![]() $I_y = (\phi _{n,y})$
be sequences of trivializations for which
$I_y = (\phi _{n,y})$
be sequences of trivializations for which
![]() $\phi _{k,x} = \phi _{k,y}$
for all
$\phi _{k,x} = \phi _{k,y}$
for all
![]() $k \geq N$
. Then we can write
$k \geq N$
. Then we can write
 $$ \begin{align} \Theta^+_{\phi_{0,x},\phi_{0,y}}(x,y) = \lim_{n \to \infty} \operatorname{\mathrm{Hol}}^{(n)}_{I_y,T}(y) ( \operatorname{\mathrm{Hol}}^{(n)}_{I_x,T}(x) )^{-1}, \end{align} $$
$$ \begin{align} \Theta^+_{\phi_{0,x},\phi_{0,y}}(x,y) = \lim_{n \to \infty} \operatorname{\mathrm{Hol}}^{(n)}_{I_y,T}(y) ( \operatorname{\mathrm{Hol}}^{(n)}_{I_x,T}(x) )^{-1}, \end{align} $$
where
 $$ \begin{align*} \operatorname{\mathrm{Hol}}^{(n)}_{I_*,T}(*) := \operatorname{\mathrm{Hol}}_{\phi_{n,*}}^{\phi_{n-1,*}}(g_{t_n}(*),g_{t_{n-1}}(*),t_{n-1}-t_n) \circ \cdots \circ \operatorname{\mathrm{Hol}}_{\phi_{1,*}}^{\phi_{0,*}}( g_{t_1}(*),*,-t_1) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hol}}^{(n)}_{I_*,T}(*) := \operatorname{\mathrm{Hol}}_{\phi_{n,*}}^{\phi_{n-1,*}}(g_{t_n}(*),g_{t_{n-1}}(*),t_{n-1}-t_n) \circ \cdots \circ \operatorname{\mathrm{Hol}}_{\phi_{1,*}}^{\phi_{0,*}}( g_{t_1}(*),*,-t_1) \end{align*} $$
is the n-step temporal holonomy measured with respect to the trivializations
![]() $I_\cdot $
at times given by T.
$I_\cdot $
at times given by T.
Proof. The convergence of the limit is simply a consequence of the fact that
![]() $d(g_{t_n}(x),g_{t_n}(y)) \to 0$
as
$d(g_{t_n}(x),g_{t_n}(y)) \to 0$
as
![]() $n \to \infty $
. More precisely, we can rewrite
$n \to \infty $
. More precisely, we can rewrite
 $$ \begin{align*} \operatorname{\mathrm{Hol}}^{(n+1)}_{I_y,T}(y) ( \operatorname{\mathrm{Hol}}_{I_x,T}^{(n+1)}(x) )^{-1} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hol}}^{(n+1)}_{I_y,T}(y) ( \operatorname{\mathrm{Hol}}_{I_x,T}^{(n+1)}(x) )^{-1} \end{align*} $$
as
 $$ \begin{align*} &\operatorname{\mathrm{Hol}}_{\phi_{n+1,y}}^{\phi_{n,y}}(g_{t_{n+1}}(y),g_{t_n}(y),t_n - t_{n+1}) \\ &\quad\circ\; (\operatorname{\mathrm{Hol}}^{(n)}_{I_y,T}(y) ( \operatorname{\mathrm{Hol}}_{I_x,T}^{(n)}(x) )^{-1}) \\ &\quad\quad\circ (\operatorname{\mathrm{Hol}}_{\phi_{n+1,x}}^{\phi_{n,x}}(g_{t_{n+1}}(x),g_{t_n}(x),t_n-t_{n+1}) )^{-1}, \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Hol}}_{\phi_{n+1,y}}^{\phi_{n,y}}(g_{t_{n+1}}(y),g_{t_n}(y),t_n - t_{n+1}) \\ &\quad\circ\; (\operatorname{\mathrm{Hol}}^{(n)}_{I_y,T}(y) ( \operatorname{\mathrm{Hol}}_{I_x,T}^{(n)}(x) )^{-1}) \\ &\quad\quad\circ (\operatorname{\mathrm{Hol}}_{\phi_{n+1,x}}^{\phi_{n,x}}(g_{t_{n+1}}(x),g_{t_n}(x),t_n-t_{n+1}) )^{-1}, \end{align*} $$
and because
![]() $f_t$
is
$f_t$
is
![]() $C^1$
, we see that
$C^1$
, we see that
 $\operatorname {\mathrm {Hol}}_{\phi _{n+1,x}}^{\phi _{n,x}}(g_{t_{n+1}}(x),g_{t_n}(x))$
must also be locally
$\operatorname {\mathrm {Hol}}_{\phi _{n+1,x}}^{\phi _{n,x}}(g_{t_{n+1}}(x),g_{t_n}(x))$
must also be locally
![]() $C^1$
in
$C^1$
in
![]() $g_{t_{n+1}}(x)$
. Since
$g_{t_{n+1}}(x)$
. Since
![]() $d_N(g_{t_{n+1}}(y),g_{t_{n+1}}(x))$
decay exponentially fast as
$d_N(g_{t_{n+1}}(y),g_{t_{n+1}}(x))$
decay exponentially fast as
![]() $n \to \infty $
and the trivializations
$n \to \infty $
and the trivializations
![]() $I_x$
and
$I_x$
and
![]() $I_y$
eventually agree, we see that
$I_y$
eventually agree, we see that
 $$ \begin{align*} d_G ( \operatorname{\mathrm{Hol}}_{\phi_{n+1,y}}^{\phi_{n,y}}(g_{t_{n+1}}(y),g_{t_n}(y),t_n-t_{n+1}) , \operatorname{\mathrm{Hol}}_{\phi_{n+1,x}}^{\phi_{n,x}}(g_{t_{n+1}}(x),g_{t_n}(x),t_n-t_{n+1}) ) \end{align*} $$
$$ \begin{align*} d_G ( \operatorname{\mathrm{Hol}}_{\phi_{n+1,y}}^{\phi_{n,y}}(g_{t_{n+1}}(y),g_{t_n}(y),t_n-t_{n+1}) , \operatorname{\mathrm{Hol}}_{\phi_{n+1,x}}^{\phi_{n,x}}(g_{t_{n+1}}(x),g_{t_n}(x),t_n-t_{n+1}) ) \end{align*} $$
must also decay exponentially fast. In particular, for any
![]() $h \in G$
, this means that
$h \in G$
, this means that
 $$ \begin{align*} &d_G ( \operatorname{\mathrm{Hol}}_{\phi_{n+1,y}}^{\phi_{n,y}}(g_{t_{n+1}}(y),g_{t_n}(y),t_n-t_{n+1}) \circ h\\ &\quad\circ (\operatorname{\mathrm{Hol}}_{\phi_{n+1,x}}^{\phi_{n,x}}(g_{t_{n+1}}(x),g_{t_n}(x),t_n-t_{n+1}))^{-1},h ) \end{align*} $$
$$ \begin{align*} &d_G ( \operatorname{\mathrm{Hol}}_{\phi_{n+1,y}}^{\phi_{n,y}}(g_{t_{n+1}}(y),g_{t_n}(y),t_n-t_{n+1}) \circ h\\ &\quad\circ (\operatorname{\mathrm{Hol}}_{\phi_{n+1,x}}^{\phi_{n,x}}(g_{t_{n+1}}(x),g_{t_n}(x),t_n-t_{n+1}))^{-1},h ) \end{align*} $$
decays exponentially fast and, hence,
 $$ \begin{align*} d_G( \operatorname{\mathrm{Hol}}^{(n+1)}_{I_y, T}(y) ( \operatorname{\mathrm{Hol}}^{(n+1)}_{I_x, T}(x) )^{-1}, \operatorname{\mathrm{Hol}}^{(n)}_{I_y, T}(y) ( \operatorname{\mathrm{Hol}}^{(n)}_{I_x, T}(x) )^{-1} ) \end{align*} $$
$$ \begin{align*} d_G( \operatorname{\mathrm{Hol}}^{(n+1)}_{I_y, T}(y) ( \operatorname{\mathrm{Hol}}^{(n+1)}_{I_x, T}(x) )^{-1}, \operatorname{\mathrm{Hol}}^{(n)}_{I_y, T}(y) ( \operatorname{\mathrm{Hol}}^{(n)}_{I_x, T}(x) )^{-1} ) \end{align*} $$
decays exponentially fast as
![]() $n \to \infty $
. As G is complete, the limit must exist. A similar argument shows that this limit is, in fact, equal to
$n \to \infty $
. As G is complete, the limit must exist. A similar argument shows that this limit is, in fact, equal to
 $\Theta ^+_{\phi _{0,x},\phi _{0,y}}(x, y)$
: because the unstable foliation of
$\Theta ^+_{\phi _{0,x},\phi _{0,y}}(x, y)$
: because the unstable foliation of
![]() $f_t$
is invariant under the flow, we can rewrite
$f_t$
is invariant under the flow, we can rewrite
 $$ \begin{align*} \Theta^+_{\phi_{0,x},\phi_{0,y}}(x, y) \end{align*} $$
$$ \begin{align*} \Theta^+_{\phi_{0,x},\phi_{0,y}}(x, y) \end{align*} $$
as
 $$ \begin{align} \operatorname{\mathrm{Hol}}^{(n)}_{I_y,T}(y) \circ \Theta^+_{\phi_{n,x},\phi_{n,y}}(g_{t_n}(x), g_{t_n}(y)) \circ ( \operatorname{\mathrm{Hol}}^{(n)}_{I_x, T}(x) )^{-1} \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Hol}}^{(n)}_{I_y,T}(y) \circ \Theta^+_{\phi_{n,x},\phi_{n,y}}(g_{t_n}(x), g_{t_n}(y)) \circ ( \operatorname{\mathrm{Hol}}^{(n)}_{I_x, T}(x) )^{-1} \end{align} $$
for any
![]() $n> 0$
and any sequences
$n> 0$
and any sequences
![]() $I_x, I_y$
and T as previously. As
$I_x, I_y$
and T as previously. As
![]() $t_n \to -\infty $
,
$t_n \to -\infty $
,
![]() $d_N(g_{t_n}(x), g_{t_n}(y))$
decreases exponentially fast, and so
$d_N(g_{t_n}(x), g_{t_n}(y))$
decreases exponentially fast, and so
 $\Theta ^+_{\phi _{n,x},\phi _{n,y}}(g_{t_n}(x), g_{t_n}(y))$
converges to the identity in G. Of course, this means that, as
$\Theta ^+_{\phi _{n,x},\phi _{n,y}}(g_{t_n}(x), g_{t_n}(y))$
converges to the identity in G. Of course, this means that, as
![]() $n \to \infty $
, (4.2) converges to the limit in (4.1). As the expression in (4.2) is constant at
$n \to \infty $
, (4.2) converges to the limit in (4.1). As the expression in (4.2) is constant at
 $\Theta ^+_{\phi _{0,x},\phi _{0,y}}(x,y)$
, this proves the proposition.
$\Theta ^+_{\phi _{0,x},\phi _{0,y}}(x,y)$
, this proves the proposition.
We need to understand the infinitesimal behaviour of the stable and unstable foliations: rather than working with the unstable holonomy as defined, we instead consider its derivative along a leaf of the unstable foliation.
Proposition 4.2. The unstable holonomy
 $\Theta ^+_{\phi _1, \phi _2}(x,y)$
is simultaneously
$\Theta ^+_{\phi _1, \phi _2}(x,y)$
is simultaneously
![]() $C^1$
in x and y, as x and y vary in a fixed leaf of the strong unstable foliation of
$C^1$
in x and y, as x and y vary in a fixed leaf of the strong unstable foliation of
![]() $g_t$
, and within charts associated with fixed
$g_t$
, and within charts associated with fixed
![]() $C^1$
trivializations
$C^1$
trivializations
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
.
$\phi _2$
.
Proof. This follows immediately from our hypotheses on the regularity of
![]() $f_t$
, which imply that the leaves of the strong unstable foliation of
$f_t$
, which imply that the leaves of the strong unstable foliation of
![]() $f_t$
are
$f_t$
are
![]() $C^1$
.
$C^1$
.
Definition 4.3. Fix
![]() $x \in N$
, a trivialization
$x \in N$
, a trivialization
![]() $\phi $
defined near x and a vector
$\phi $
defined near x and a vector
 $w \in T^1_xW^{su}_{g_t}(x)$
. We define the infinitesimal holonomy at x in the direction of w to be the element
$w \in T^1_xW^{su}_{g_t}(x)$
. We define the infinitesimal holonomy at x in the direction of w to be the element

of the Lie algebra
![]() $\mathfrak g$
of G. Let
$\mathfrak g$
of G. Let
![]() $\epsilon> 0$
be small enough that
$\epsilon> 0$
be small enough that
![]() $\phi $
is defined over
$\phi $
is defined over
![]() $B_\epsilon (x)$
. The
$B_\epsilon (x)$
. The
![]() $\epsilon $
-infinitesimal transitivity group at x is defined to be the linear span
$\epsilon $
-infinitesimal transitivity group at x is defined to be the linear span
 $$ \begin{align*} \mathfrak h_\epsilon^\phi(x) := \operatorname*{\mathrm{span}}_{y,w} (X_{w'}(y) - X_w(x)) \end{align*} $$
$$ \begin{align*} \mathfrak h_\epsilon^\phi(x) := \operatorname*{\mathrm{span}}_{y,w} (X_{w'}(y) - X_w(x)) \end{align*} $$
taken over all
![]() $y \in W^{ss}_\epsilon (x)$
and
$y \in W^{ss}_\epsilon (x)$
and
 $w \in T^1_xW^{su}_{g_t}(x)$
. Here,
$w \in T^1_xW^{su}_{g_t}(x)$
. Here,
![]() $w'$
denotes the pushforward of w to
$w'$
denotes the pushforward of w to
 $T^1_yW^{su}_{g_t}(y)$
along the leaves of the centre stable foliation of
$T^1_yW^{su}_{g_t}(y)$
along the leaves of the centre stable foliation of
![]() $g_t$
.
$g_t$
.
We soon verify that
![]() $\mathfrak h^\phi (x)$
is largely independent of the choice of trivialization
$\mathfrak h^\phi (x)$
is largely independent of the choice of trivialization
![]() $\phi $
, but it is worth making a few comments first.
$\phi $
, but it is worth making a few comments first.
Remark 4.3. Under our hypotheses, the foliation
![]() $W^{ws}_{g_t}$
is
$W^{ws}_{g_t}$
is
![]() $C^1$
, and so the holonomy it induces between the leaves of the foliation
$C^1$
, and so the holonomy it induces between the leaves of the foliation
![]() $W^{su}_{g_t}$
is also
$W^{su}_{g_t}$
is also
![]() $C^1$
. This is necessary for the pushforward of
$C^1$
. This is necessary for the pushforward of
 $w \in T^1_yW^{su}_{g_t}(y)$
in Definition 4.3 to make sense.
$w \in T^1_yW^{su}_{g_t}(y)$
in Definition 4.3 to make sense.
Remark 4.4. It is necessary to consider the relative infinitesimal holonomy, as we did in Definition 4.3. As we show in the course of proving Proposition 4.6, the vector
 $X_w^\phi (x)$
in Definition 4.3 is extremely sensitive to the choice of trivialization
$X_w^\phi (x)$
in Definition 4.3 is extremely sensitive to the choice of trivialization
![]() $\phi $
. For instance, it is certainly possible for
$\phi $
. For instance, it is certainly possible for
 $X_w^\phi (x)$
to be zero for all
$X_w^\phi (x)$
to be zero for all
 $w \in T^1_xW^{su}_{g_t}(x)$
if the trivialization
$w \in T^1_xW^{su}_{g_t}(x)$
if the trivialization
![]() $\phi $
is built to be constant along the leaves of the strong unstable foliation, and the existence of such trivializations will be extremely helpful in the course of proving Theorem 4.11.
$\phi $
is built to be constant along the leaves of the strong unstable foliation, and the existence of such trivializations will be extremely helpful in the course of proving Theorem 4.11.
Remark 4.5. The vectors
 $X_w^\phi (x)$
and
$X_w^\phi (x)$
and
 $X_{w'}^\phi (y)$
vary continuously in x and w, by Proposition 4.2. However, because
$X_{w'}^\phi (y)$
vary continuously in x and w, by Proposition 4.2. However, because
![]() $\mathfrak h_\epsilon (x)$
is defined as the linear span of continuously varying vectors, it is only lower semi-continuous. In particular, there can be singular sets where the dimension of
$\mathfrak h_\epsilon (x)$
is defined as the linear span of continuously varying vectors, it is only lower semi-continuous. In particular, there can be singular sets where the dimension of
![]() $\mathfrak h_\epsilon (x)$
jumps down.
$\mathfrak h_\epsilon (x)$
jumps down.
It turns out that
 $\mathfrak h^\phi _\epsilon (x)$
will typically be independent of
$\mathfrak h^\phi _\epsilon (x)$
will typically be independent of
![]() $\epsilon $
, though we do not prove this directly. We show instead that, if
$\epsilon $
, though we do not prove this directly. We show instead that, if
![]() $f_t$
is locally G-accessible, then
$f_t$
is locally G-accessible, then
![]() $\mathfrak h_\epsilon (x)$
is generically equal to
$\mathfrak h_\epsilon (x)$
is generically equal to
![]() $\mathfrak g$
. For most of what follows, we treat
$\mathfrak g$
. For most of what follows, we treat
![]() $\epsilon> 0$
as a fixed constant with no particular restrictions. Our first important calculation is that the conjugacy class of
$\epsilon> 0$
as a fixed constant with no particular restrictions. Our first important calculation is that the conjugacy class of
 $\mathfrak h_\epsilon ^\phi (x)$
does not depend on the trivialization
$\mathfrak h_\epsilon ^\phi (x)$
does not depend on the trivialization
![]() $\phi $
, if the trivializations are chosen appropriately.
$\phi $
, if the trivializations are chosen appropriately.
Proposition 4.6. Fix
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
![]() $x \in N$
and trivializations
$x \in N$
and trivializations
![]() $\phi _{i} \colon \pi ^{-1}(V_{i}) \to V_{i} \times F$
for
$\phi _{i} \colon \pi ^{-1}(V_{i}) \to V_{i} \times F$
for
![]() $i = 1,2$
. If
$i = 1,2$
. If
![]() $B_\epsilon (x) \subset V_{i}$
, then
$B_\epsilon (x) \subset V_{i}$
, then
 $$ \begin{align*} \mathfrak h_\epsilon^{\phi_2}(x) = \operatorname{\mathrm{Ad}}_{\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x)} (\mathfrak h_\epsilon^{\phi_1}(x)) \end{align*} $$
$$ \begin{align*} \mathfrak h_\epsilon^{\phi_2}(x) = \operatorname{\mathrm{Ad}}_{\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x)} (\mathfrak h_\epsilon^{\phi_1}(x)) \end{align*} $$
so long as
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
have constant projection to F along each leaf of the strong stable foliation of
$\phi _2$
have constant projection to F along each leaf of the strong stable foliation of
![]() $f_t$
and each flowline of
$f_t$
and each flowline of
![]() $f_t$
.
$f_t$
.
Here,
 $\operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}(x) \colon F \to F$
is used to denote the isometry induced by the identity map
$\operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}(x) \colon F \to F$
is used to denote the isometry induced by the identity map
![]() $\pi ^{-1}(x) \to \pi ^{-1}(x)$
with the domain and target identified with F via
$\pi ^{-1}(x) \to \pi ^{-1}(x)$
with the domain and target identified with F via
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
, respectively.
$\phi _2$
, respectively.
Proof. We can relate the unstable holonomies between x and
![]() $u \in W^{su}_{g_t}(x)$
with respect to
$u \in W^{su}_{g_t}(x)$
with respect to
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
by
$\phi _2$
by
 $$ \begin{align} \Theta^+_{\phi_2,\phi_2} ( x,u ) = \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(u) \circ \Theta^+_{\phi_1,\phi_1}( x,u ) \circ ( \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x) )^{-1} \end{align} $$
$$ \begin{align} \Theta^+_{\phi_2,\phi_2} ( x,u ) = \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(u) \circ \Theta^+_{\phi_1,\phi_1}( x,u ) \circ ( \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x) )^{-1} \end{align} $$
by definition. We now simply take the derivative of each side of (4.3) with respect to u at
![]() $u = x$
; in the notation of Definition 4.3, this becomes
$u = x$
; in the notation of Definition 4.3, this becomes
 $$ \begin{align} X_w^{\phi_2}(x) = \operatorname{\mathrm{Ad}}_{\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x)} ( X_{w\phantom{'}}^{\phi_1}(x) ) + ((d{\kern-1.1pt}R)_{(\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x))^{-1}} \circ d( \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2} )_x )(w) \end{align} $$
$$ \begin{align} X_w^{\phi_2}(x) = \operatorname{\mathrm{Ad}}_{\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x)} ( X_{w\phantom{'}}^{\phi_1}(x) ) + ((d{\kern-1.1pt}R)_{(\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x))^{-1}} \circ d( \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2} )_x )(w) \end{align} $$
for any
 $w \in T^1_xW^{su}_{g_t}(x)$
, where
$w \in T^1_xW^{su}_{g_t}(x)$
, where
![]() $d{\kern-1.1pt}R$
denotes the derivative of right multiplication in G. Given any
$d{\kern-1.1pt}R$
denotes the derivative of right multiplication in G. Given any
![]() $y \in W^{ss}_{\epsilon }(x)$
and
$y \in W^{ss}_{\epsilon }(x)$
and
![]() $w'$
corresponding to w as in Definition 4.3, exactly the same calculation yields
$w'$
corresponding to w as in Definition 4.3, exactly the same calculation yields
 $$ \begin{align} X_{w'}^{\phi_2}(y) = \operatorname{\mathrm{Ad}}_{\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(y)} ( X_{w'}^{\phi_1}(y) ) + ((d{\kern-1.1pt}R)_{(\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(y))^{-1}} \circ d( \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2} )_y )({w'}), \end{align} $$
$$ \begin{align} X_{w'}^{\phi_2}(y) = \operatorname{\mathrm{Ad}}_{\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(y)} ( X_{w'}^{\phi_1}(y) ) + ((d{\kern-1.1pt}R)_{(\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(y))^{-1}} \circ d( \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2} )_y )({w'}), \end{align} $$
assuming, of course, that y is sufficiently close to x that we are able to use the same trivializations
![]() $\phi _1, \phi _2$
. As both trivializations are constant along the strong stable foliation of
$\phi _1, \phi _2$
. As both trivializations are constant along the strong stable foliation of
![]() $f_t$
and we chose
$f_t$
and we chose
![]() $y \in W^{ss}_{\epsilon }(x)$
, we clearly have
$y \in W^{ss}_{\epsilon }(x)$
, we clearly have
 $\operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}(x) = \operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}(y)$
and, hence,
$\operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}(x) = \operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}(y)$
and, hence,
 $$ \begin{align*} (d{\kern-1.1pt}R)_{(\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x))^{-1}} = (d{\kern-1.1pt}R)_{(\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(y))^{-1}} \end{align*} $$
$$ \begin{align*} (d{\kern-1.1pt}R)_{(\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x))^{-1}} = (d{\kern-1.1pt}R)_{(\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(y))^{-1}} \end{align*} $$
as functions
![]() $T^1G \to T^1G$
. Moreover, because the trivializations are also constant along the flowlines of
$T^1G \to T^1G$
. Moreover, because the trivializations are also constant along the flowlines of
![]() $f_t$
, we see that
$f_t$
, we see that
 $\operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}$
must be constant along the leaves of the centre stable foliation of
$\operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}$
must be constant along the leaves of the centre stable foliation of
![]() $g_t$
. Hence, we must have
$g_t$
. Hence, we must have
 $$ \begin{align*} (d( \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2} )_x)(w) = ( d( \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2} )_y )(w') \end{align*} $$
$$ \begin{align*} (d( \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2} )_x)(w) = ( d( \operatorname{\mathrm{id}}_{\phi_1}^{\phi_2} )_y )(w') \end{align*} $$
for all
 $w \in T^1_xW^{su}_{g_t}(x)$
. Subtracting (4.4) from (4.5) and using the fact that
$w \in T^1_xW^{su}_{g_t}(x)$
. Subtracting (4.4) from (4.5) and using the fact that
 $\operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}(x) = \operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}(y)$
, we then obtain
$\operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}(x) = \operatorname {\mathrm {id}}_{\phi _1}^{\phi _2}(y)$
, we then obtain
 $$ \begin{align*} X_{w'}^{\phi_2}(y) - X_{w}^{\phi_2}(x) = \operatorname{\mathrm{Ad}}_{\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(y)} ( X_{w'}^{\phi_1}(y) ) - \operatorname{\mathrm{Ad}}_{\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x)} ( X_{w \phantom{'}}^{\phi_1}(x) ) \end{align*} $$
$$ \begin{align*} X_{w'}^{\phi_2}(y) - X_{w}^{\phi_2}(x) = \operatorname{\mathrm{Ad}}_{\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(y)} ( X_{w'}^{\phi_1}(y) ) - \operatorname{\mathrm{Ad}}_{\operatorname{\mathrm{id}}_{\phi_1}^{\phi_2}(x)} ( X_{w \phantom{'}}^{\phi_1}(x) ) \end{align*} $$
as desired.
There is an analogous relation between the
![]() $\epsilon $
-infinitesimal transitivity groups at points along a flowline of
$\epsilon $
-infinitesimal transitivity groups at points along a flowline of
![]() $g_t$
, though the expansion of the unstable leaves prevent us from obtain an equality in this case.
$g_t$
, though the expansion of the unstable leaves prevent us from obtain an equality in this case.
Proposition 4.7. Fix
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
![]() $x \in N$
and
$x \in N$
and
![]() $t> 0$
. Let
$t> 0$
. Let
![]() $\phi _x$
and
$\phi _x$
and
![]() $\phi _{g_t(x)}$
be trivializations near x and
$\phi _{g_t(x)}$
be trivializations near x and
![]() $g_t(x)$
for which
$g_t(x)$
for which
![]() $B_\epsilon (x) \subset V_x$
and
$B_\epsilon (x) \subset V_x$
and
![]() $B_\epsilon (g_t(x)) \subset V_{g_t(x)}$
, and write h for the temporal holonomy
$B_\epsilon (g_t(x)) \subset V_{g_t(x)}$
, and write h for the temporal holonomy
 $$ \begin{align*} h(x) := \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_{g_t(x)}}( x, g_t(x),t) \end{align*} $$
$$ \begin{align*} h(x) := \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_{g_t(x)}}( x, g_t(x),t) \end{align*} $$
measured with respect to
![]() $\phi _x$
and
$\phi _x$
and
![]() $\phi _{g_t}(x)$
. We then have
$\phi _{g_t}(x)$
. We then have
 $$ \begin{align*} \operatorname{\mathrm{Ad}}_{h(x)} ( \mathfrak h_\epsilon^{\phi_x}(x) ) \subset \mathfrak h_\epsilon^{\phi_{g_t(x)}}(g_t(x)) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ad}}_{h(x)} ( \mathfrak h_\epsilon^{\phi_x}(x) ) \subset \mathfrak h_\epsilon^{\phi_{g_t(x)}}(g_t(x)) \end{align*} $$
so long as
![]() $\phi _x$
and
$\phi _x$
and
![]() $\phi _{g_t(x)}$
have constant projection to F along each leaf of the strong stable foliation of
$\phi _{g_t(x)}$
have constant projection to F along each leaf of the strong stable foliation of
![]() $f_t$
and each flowline of
$f_t$
and each flowline of
![]() $f_t$
.
$f_t$
.
Proof. By Proposition 4.1, we have
 $$ \begin{align*} \Theta^+_{\phi_2,\phi_2}(g_t(x), g_t(u)) = h(u) \circ \Theta^+_{\phi_1, \phi_1}(x,u) \circ ( h(x) )^{-1} \end{align*} $$
$$ \begin{align*} \Theta^+_{\phi_2,\phi_2}(g_t(x), g_t(u)) = h(u) \circ \Theta^+_{\phi_1, \phi_1}(x,u) \circ ( h(x) )^{-1} \end{align*} $$
so long as u is sufficiently close to x. Noting the resemblance to (4.3), simply repeating our calculations in Proposition 4.6 yields
 $$ \begin{align*} X_{w'}^{\phi_{g_t(x)}}(g_t(y)) - X_{w}^{\phi_{g_t(x)}}(g_t(x)) = \operatorname{\mathrm{Ad}}_{h(x)} ( X_{w'}^{\phi_x}(y) ) - \operatorname{\mathrm{Ad}}_{h(x)} ( X_{w\phantom{'}}^{\phi_x}(x) ) \end{align*} $$
$$ \begin{align*} X_{w'}^{\phi_{g_t(x)}}(g_t(y)) - X_{w}^{\phi_{g_t(x)}}(g_t(x)) = \operatorname{\mathrm{Ad}}_{h(x)} ( X_{w'}^{\phi_x}(y) ) - \operatorname{\mathrm{Ad}}_{h(x)} ( X_{w\phantom{'}}^{\phi_x}(x) ) \end{align*} $$
for all
![]() $y \in W^{ss}_{\epsilon }(x)$
and all
$y \in W^{ss}_{\epsilon }(x)$
and all
 $w \in T^1_xW^{su}_{g_t}(x)$
. This completes the proof; note that we do not obtain equality this time because the strong stable leaves for
$w \in T^1_xW^{su}_{g_t}(x)$
. This completes the proof; note that we do not obtain equality this time because the strong stable leaves for
![]() $g_t$
contract, and there will be
$g_t$
contract, and there will be
![]() $y' \in W^{ss}_{\epsilon }(g_t(x))$
that are not of the form
$y' \in W^{ss}_{\epsilon }(g_t(x))$
that are not of the form
![]() $g_t(y)$
for
$g_t(y)$
for
![]() $y \in W^{ss}_\epsilon (x)$
.
$y \in W^{ss}_\epsilon (x)$
.
Note that Proposition 4.7 only yields an inclusion of the
![]() $\epsilon $
-infinitesimal transitivity groups, and only in forward time. Our goal is to show that
$\epsilon $
-infinitesimal transitivity groups, and only in forward time. Our goal is to show that
 $\mathfrak h_\epsilon ^\phi (x)$
is exactly
$\mathfrak h_\epsilon ^\phi (x)$
is exactly
![]() $\mathfrak g$
at every
$\mathfrak g$
at every
![]() $x \in N$
; unfortunately, the proof of Proposition 4.7 suggests that even the dimension of
$x \in N$
; unfortunately, the proof of Proposition 4.7 suggests that even the dimension of
![]() $\mathfrak h_\epsilon (x)$
may fail to be constant in general. Fortunately, given the topological transitivity of
$\mathfrak h_\epsilon (x)$
may fail to be constant in general. Fortunately, given the topological transitivity of
![]() $g_t$
, what we have proven so far is enough to show that the dimension is constant on a large set.
$g_t$
, what we have proven so far is enough to show that the dimension is constant on a large set.
In light of Proposition 4.6, we can be somewhat cavalier in specifying the trivialization
![]() $\phi $
used in defining
$\phi $
used in defining
 $\mathfrak h_\epsilon ^\phi (x)$
, if we are solely concerned with the dimension and restrict our attention to trivializations that satisfy the hypotheses of the proposition. We henceforth always assume that every trivialization we work with has constant projection to F along the strong stable leaves and flowlines of
$\mathfrak h_\epsilon ^\phi (x)$
, if we are solely concerned with the dimension and restrict our attention to trivializations that satisfy the hypotheses of the proposition. We henceforth always assume that every trivialization we work with has constant projection to F along the strong stable leaves and flowlines of
![]() $f_t$
.
$f_t$
.
Corollary 4.8. Fix a collection of trivializations
![]() $\phi _1, \ldots , \phi _k$
defined over a cover
$\phi _1, \ldots , \phi _k$
defined over a cover
![]() $V_1, \ldots , V_k$
of N, and let
$V_1, \ldots , V_k$
of N, and let
![]() $\epsilon> 0$
be the Lebesgue number of this cover. Then
$\epsilon> 0$
be the Lebesgue number of this cover. Then
![]() $\dim \mathfrak h_\epsilon ^*(\cdot )$
attains its maximum value on an open, dense subset of full measure.
$\dim \mathfrak h_\epsilon ^*(\cdot )$
attains its maximum value on an open, dense subset of full measure.
Proof. Let
![]() $x \in N$
be a point at which
$x \in N$
be a point at which
![]() $\mathfrak h_\epsilon ^*(x)$
has maximal dimension. As
$\mathfrak h_\epsilon ^*(x)$
has maximal dimension. As
![]() $\mathfrak h_\epsilon ^*(\cdot )$
is lower semi-continuous, it has maximal dimension on an open neighbourhood W containing x. By Proposition 4.7,
$\mathfrak h_\epsilon ^*(\cdot )$
is lower semi-continuous, it has maximal dimension on an open neighbourhood W containing x. By Proposition 4.7,
![]() $\mathfrak h_\epsilon ^*(\cdot )$
therefore has maximal dimension on an open set containing the forward orbit of
$\mathfrak h_\epsilon ^*(\cdot )$
therefore has maximal dimension on an open set containing the forward orbit of
![]() $g_t$
. This is a dense set if
$g_t$
. This is a dense set if
![]() $g_t$
is topologically transitive.
$g_t$
is topologically transitive.
As
![]() $g_t$
is ergodic and
$g_t$
is ergodic and
![]() $\dim \mathfrak h_\epsilon ^*(\cdot )$
is measurable, it must be constant almost everywhere. The measure
$\dim \mathfrak h_\epsilon ^*(\cdot )$
is measurable, it must be constant almost everywhere. The measure
![]() $\nu $
is an equilibrium measure with a Hölder potential and therefore has full support; hence, the open and dense set on which
$\nu $
is an equilibrium measure with a Hölder potential and therefore has full support; hence, the open and dense set on which
![]() $\dim \mathfrak h_\epsilon ^*(\cdot )$
has maximal dimension must also have full measure.
$\dim \mathfrak h_\epsilon ^*(\cdot )$
has maximal dimension must also have full measure.
Our next objective is to relate the
![]() $\epsilon $
-infinitesimal transitivity groups between points along a leaf of the strong unstable foliation of
$\epsilon $
-infinitesimal transitivity groups between points along a leaf of the strong unstable foliation of
![]() $g_t$
. If we indeed had equality in Proposition 4.7, this would be a relatively straightforward application of Proposition 4.1. The lack of equality makes such an approach impossible, but we can still argue as in Corollary 4.8.
$g_t$
. If we indeed had equality in Proposition 4.7, this would be a relatively straightforward application of Proposition 4.1. The lack of equality makes such an approach impossible, but we can still argue as in Corollary 4.8.
Lemma 4.9. Fix
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
![]() $x \in N$
and
$x \in N$
and
![]() $y \in W^{su}_{g_t}(x)$
, along with trivializations
$y \in W^{su}_{g_t}(x)$
, along with trivializations
![]() $\phi _x$
and
$\phi _x$
and
![]() $\phi _y$
for which we have
$\phi _y$
for which we have
![]() $B_{2\epsilon }(x) \subset V_x$
and
$B_{2\epsilon }(x) \subset V_x$
and
![]() $B_\epsilon (y) \subset V_y$
. If x is backwards-recurrent under
$B_\epsilon (y) \subset V_y$
. If x is backwards-recurrent under
![]() $g_t$
and
$g_t$
and
![]() $\dim \mathfrak h_\epsilon ^*(x)$
is maximal, then
$\dim \mathfrak h_\epsilon ^*(x)$
is maximal, then
 $$ \begin{align*} \mathfrak h_\epsilon^{\phi_y}(y) = \operatorname{\mathrm{Ad}}_{\Theta^+_{\phi_x,\phi_y}(x,y)}( \mathfrak h_\epsilon^{\phi_x}(x) ) \end{align*} $$
$$ \begin{align*} \mathfrak h_\epsilon^{\phi_y}(y) = \operatorname{\mathrm{Ad}}_{\Theta^+_{\phi_x,\phi_y}(x,y)}( \mathfrak h_\epsilon^{\phi_x}(x) ) \end{align*} $$
and, in particular,
![]() $\dim \mathfrak h^*_\epsilon (\cdot )$
is constant on
$\dim \mathfrak h^*_\epsilon (\cdot )$
is constant on
![]() $W^{su}_{g_t}(x)$
.
$W^{su}_{g_t}(x)$
.
Proof. As
![]() $\dim \mathfrak h^*_\epsilon (\cdot )$
is lower semi-continuous, there is an open set
$\dim \mathfrak h^*_\epsilon (\cdot )$
is lower semi-continuous, there is an open set
![]() $W \subset B_\epsilon (x)$
on which it is maximal. Because x is backwards recurrent, we can find a monotonic sequence of times
$W \subset B_\epsilon (x)$
on which it is maximal. Because x is backwards recurrent, we can find a monotonic sequence of times
![]() $T = \{ t_n \}$
with
$T = \{ t_n \}$
with
![]() $t_n \to -\infty $
for which
$t_n \to -\infty $
for which
![]() $g_{t_n}(x) \in W$
for each
$g_{t_n}(x) \in W$
for each
![]() $n> 0$
. Moreover, we can suppose that
$n> 0$
. Moreover, we can suppose that
![]() $t_1$
is large enough that we also have
$t_1$
is large enough that we also have
![]() $g_{t_n}(y) \in W$
for each
$g_{t_n}(y) \in W$
for each
![]() $n> 0$
. Now, write
$n> 0$
. Now, write
 $$ \begin{align*} h^{(n)}(x) := \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_x}(g_{t_n}(x),g_{t_{n-1}}(x),t_{n-1}-t_n) \circ \cdots \circ \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_x}( g_{t_1}(x),x,-t_1 ) \end{align*} $$
$$ \begin{align*} h^{(n)}(x) := \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_x}(g_{t_n}(x),g_{t_{n-1}}(x),t_{n-1}-t_n) \circ \cdots \circ \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_x}( g_{t_1}(x),x,-t_1 ) \end{align*} $$
and
 $$ \begin{align*} h^{(n)}(y) := \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_x}(g_{t_n}(y),g_{t_{n-1}}(y),t_{n-1}-t_n) \circ \cdots \circ \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_y}( g_{t_1}(y),y, -t_1) \end{align*} $$
$$ \begin{align*} h^{(n)}(y) := \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_x}(g_{t_n}(y),g_{t_{n-1}}(y),t_{n-1}-t_n) \circ \cdots \circ \operatorname{\mathrm{Hol}}_{\phi_x}^{\phi_y}( g_{t_1}(y),y, -t_1) \end{align*} $$
for the n-step holonomies at
![]() $g_{t_n}(x)$
and
$g_{t_n}(x)$
and
![]() $g_{t_n}(y)$
. As we have
$g_{t_n}(y)$
. As we have
![]() $g_{t_n}(x), g_{t_n}(y) \in W$
by construction, we have
$g_{t_n}(x), g_{t_n}(y) \in W$
by construction, we have
 $$ \begin{align*} \operatorname{\mathrm{Ad}}_{h^{(n)}(x)}( \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(x) ) ) = \mathfrak h_\epsilon^{\phi_x}(x) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ad}}_{h^{(n)}(x)}( \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(x) ) ) = \mathfrak h_\epsilon^{\phi_x}(x) \end{align*} $$
and
 $$ \begin{align*} \operatorname{\mathrm{Ad}}_{h^{(n)}(y)}( \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(y) ) ) = \mathfrak h_\epsilon^{\phi_y}(y) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ad}}_{h^{(n)}(y)}( \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(y) ) ) = \mathfrak h_\epsilon^{\phi_y}(y) \end{align*} $$
by Proposition 4.7; note that we have implicitly used the fact that
![]() $B_{2\epsilon }(x) \subset V_x$
in writing
$B_{2\epsilon }(x) \subset V_x$
in writing
 $\mathfrak h_\epsilon ^{\phi _x}( g_{t_n}(x) )$
and
$\mathfrak h_\epsilon ^{\phi _x}( g_{t_n}(x) )$
and
 $\mathfrak h_\epsilon ^{\phi _x}( g_{t_n}(y) )$
, where
$\mathfrak h_\epsilon ^{\phi _x}( g_{t_n}(y) )$
, where
![]() $V_x$
is the chart over which
$V_x$
is the chart over which
![]() $\phi _x$
is defined. By rearranging these equations, we see that
$\phi _x$
is defined. By rearranging these equations, we see that
 $$ \begin{align*} d_{\operatorname{\mathrm{Gr}}(\dim \mathfrak h^*_\epsilon(x),\mathfrak g)}( \mathfrak h_\epsilon^{\phi_y}(y), \operatorname{\mathrm{Ad}}_{h^{(n)}(y) ( h^{(n)}(x) )^{-1}}( \mathfrak h_\epsilon^{\phi_x}(x) ) ) \end{align*} $$
$$ \begin{align*} d_{\operatorname{\mathrm{Gr}}(\dim \mathfrak h^*_\epsilon(x),\mathfrak g)}( \mathfrak h_\epsilon^{\phi_y}(y), \operatorname{\mathrm{Ad}}_{h^{(n)}(y) ( h^{(n)}(x) )^{-1}}( \mathfrak h_\epsilon^{\phi_x}(x) ) ) \end{align*} $$
is equal to
 $$ \begin{align*} d_{\operatorname{\mathrm{Gr}}(\dim \mathfrak h^*_\epsilon(x),\mathfrak g)}( \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(y) ), \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(x) ) ), \end{align*} $$
$$ \begin{align*} d_{\operatorname{\mathrm{Gr}}(\dim \mathfrak h^*_\epsilon(x),\mathfrak g)}( \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(y) ), \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(x) ) ), \end{align*} $$
where the distances are measured in the standard metric on the Grassmannian of
![]() $(\dim \mathfrak h^*_\epsilon (x))$
-dimensional subspaces of
$(\dim \mathfrak h^*_\epsilon (x))$
-dimensional subspaces of
![]() $\mathfrak g$
. As
$\mathfrak g$
. As
 $\mathfrak h_\epsilon ^{\phi _x}(\cdot )$
is lower semi-continuous and has maximal dimension on W, it must be continuous on W. Up to passage to the interior of a compact subset of W, we can assume that
$\mathfrak h_\epsilon ^{\phi _x}(\cdot )$
is lower semi-continuous and has maximal dimension on W, it must be continuous on W. Up to passage to the interior of a compact subset of W, we can assume that
![]() $\mathfrak h_\epsilon (\cdot )$
is uniformly continuous on W. Because
$\mathfrak h_\epsilon (\cdot )$
is uniformly continuous on W. Because
![]() $d_N(g_{t_n}(y),g_{t_n}(x)) \to 0$
as
$d_N(g_{t_n}(y),g_{t_n}(x)) \to 0$
as
![]() $n \to \infty $
, we must then have
$n \to \infty $
, we must then have
 $$ \begin{align*} d_{\operatorname{\mathrm{Gr}}(\dim \mathfrak h^*_\epsilon(x),\mathfrak g)}( \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(y) ), \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(x) ) ) \end{align*} $$
$$ \begin{align*} d_{\operatorname{\mathrm{Gr}}(\dim \mathfrak h^*_\epsilon(x),\mathfrak g)}( \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(y) ), \mathfrak h_\epsilon^{\phi_x}( g_{t_n}(x) ) ) \end{align*} $$
as
![]() $n \to \infty $
. This yields
$n \to \infty $
. This yields
 $$ \begin{align*} \mathfrak h_\epsilon^{\phi_y}(y) = \lim_{n \to \infty} \operatorname{\mathrm{Ad}}_{h^{(n)}(y) ( h^{(n)}(x) )^{-1}}( \mathfrak h_\epsilon^{\phi_x}(x) ), \end{align*} $$
$$ \begin{align*} \mathfrak h_\epsilon^{\phi_y}(y) = \lim_{n \to \infty} \operatorname{\mathrm{Ad}}_{h^{(n)}(y) ( h^{(n)}(x) )^{-1}}( \mathfrak h_\epsilon^{\phi_x}(x) ), \end{align*} $$
at which point we simply observe that
![]() $\operatorname {\mathrm {Ad}}_g(\cdot )$
is continuous in g and that
$\operatorname {\mathrm {Ad}}_g(\cdot )$
is continuous in g and that
![]() $h^{(n)}(y) (h^{(n)}(x))^{-1}$
converges to
$h^{(n)}(y) (h^{(n)}(x))^{-1}$
converges to
 $\Theta ^+_{\phi _x,\phi _y}(x,y)$
by Proposition 4.1.
$\Theta ^+_{\phi _x,\phi _y}(x,y)$
by Proposition 4.1.
In addition to the preceding lemma, we require its analogue for the stable holonomies. The proof is identical, and we do not repeat it.
Lemma 4.10. Fix
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
![]() $x \in N$
and
$x \in N$
and
![]() $y \in W^{ss}_{g_t}(x)$
, along with trivializations
$y \in W^{ss}_{g_t}(x)$
, along with trivializations
![]() $\phi _x$
and
$\phi _x$
and
![]() $\phi _y$
for which we have
$\phi _y$
for which we have
![]() $B_{2\epsilon }(x) \subset V_x$
and
$B_{2\epsilon }(x) \subset V_x$
and
![]() $B_\epsilon (y) \subset V_y$
. If x is forwards-recurrent under
$B_\epsilon (y) \subset V_y$
. If x is forwards-recurrent under
![]() $g_t$
and
$g_t$
and
![]() $\dim \mathfrak h^*_\epsilon (x)$
is maximal, then
$\dim \mathfrak h^*_\epsilon (x)$
is maximal, then
 $$ \begin{align*} \mathfrak h_\epsilon^{\phi_y}(y) = \operatorname{\mathrm{Ad}}_{\Theta^-_{\phi_x,\phi_y}(x,y)}( \mathfrak h_\epsilon^{\phi_x}(x) ) \end{align*} $$
$$ \begin{align*} \mathfrak h_\epsilon^{\phi_y}(y) = \operatorname{\mathrm{Ad}}_{\Theta^-_{\phi_x,\phi_y}(x,y)}( \mathfrak h_\epsilon^{\phi_x}(x) ) \end{align*} $$
and, in particular,
![]() $\dim \mathfrak h^*_\epsilon (\cdot )$
is constant on
$\dim \mathfrak h^*_\epsilon (\cdot )$
is constant on
![]() $W^{ss}_{g_t}(x)$
.
$W^{ss}_{g_t}(x)$
.
Now that we have Lemmas 4.9 and 4.10 to connect the
![]() $\epsilon $
-infinitesimal transitivity groups to the unstable and stable holonomies, respectively, we can achieve the first major goal of this section: translating the local accessibility of
$\epsilon $
-infinitesimal transitivity groups to the unstable and stable holonomies, respectively, we can achieve the first major goal of this section: translating the local accessibility of
![]() $f_t$
into an infinitesimal statement about
$f_t$
into an infinitesimal statement about
![]() $\mathfrak h_\epsilon ^*(\cdot )$
. To begin, we show that if
$\mathfrak h_\epsilon ^*(\cdot )$
. To begin, we show that if
![]() $f_t$
is G-accessible, then
$f_t$
is G-accessible, then
 $\mathfrak h_\epsilon ^\phi (x)$
must be
$\mathfrak h_\epsilon ^\phi (x)$
must be
![]() $\operatorname {\mathrm {Ad}}_G$
-invariant for any bi-recurrent
$\operatorname {\mathrm {Ad}}_G$
-invariant for any bi-recurrent
![]() $x \in N$
.
$x \in N$
.
Theorem 4.11. Fix
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
![]() $x \in N$
and a trivialization
$x \in N$
and a trivialization
![]() $\phi _x$
for which
$\phi _x$
for which
![]() $B_\epsilon (x) \subset V_x$
. Suppose that
$B_\epsilon (x) \subset V_x$
. Suppose that
![]() $2\epsilon $
is smaller than the Lebesgue number of a finite cover
$2\epsilon $
is smaller than the Lebesgue number of a finite cover
![]() $\{ V_i \}$
of N corresponding to trivializations
$\{ V_i \}$
of N corresponding to trivializations
![]() $\{ \phi _i \}$
. If x is bi-recurrent under
$\{ \phi _i \}$
. If x is bi-recurrent under
![]() $g_t$
,
$g_t$
,
 $\dim \mathfrak h_\epsilon ^{\phi _x}(x)$
is maximal and
$\dim \mathfrak h_\epsilon ^{\phi _x}(x)$
is maximal and
![]() $f_t$
is G-accessible, then
$f_t$
is G-accessible, then
 $\mathfrak h_\epsilon ^{\phi _x}(x)$
is
$\mathfrak h_\epsilon ^{\phi _x}(x)$
is
![]() $\operatorname {\mathrm {Ad}}_G$
-invariant.
$\operatorname {\mathrm {Ad}}_G$
-invariant.
Proof. Suppose that x is bi-recurrent. Fix an isometry
![]() $g \in G$
and consider a stable–unstable sequence
$g \in G$
and consider a stable–unstable sequence
![]() $x_0, x_1, \ldots , x_k, x_{k+1} = x_0$
in N with
$x_0, x_1, \ldots , x_k, x_{k+1} = x_0$
in N with
![]() $x_0 = x$
and whose total holonomy is g, where
$x_0 = x$
and whose total holonomy is g, where
![]() $x_{i+1}$
is either on the strong stable or strong unstable leaf through
$x_{i+1}$
is either on the strong stable or strong unstable leaf through
![]() $x_i$
for
$x_i$
for
![]() $g_t$
. As g is the total holonomy, we can write g as the composite
$g_t$
. As g is the total holonomy, we can write g as the composite
 $$ \begin{align*} &\operatorname{\mathrm{id}}_{\phi_{x_k}}^{\phi_{x_0}}(x_0) \circ \Theta^\pm_{\phi_{x_k},\phi_{x_k}}( x_k,x_0 ) \circ \ldots \operatorname{\mathrm{id}}_{\phi_{x_1}}^{\phi_{x_2}}(x_2)\\ &\quad\circ \Theta^\pm_{\phi_{x_1},\phi_{x_1}} ( x_1,x_2 ) \circ \operatorname{\mathrm{id}}_{\phi_{x_0}}^{\phi_{x_1}}(x_1) \circ \Theta^\pm_{\phi_{x_0},\phi_{x_0}}( x_0,x_1 ), \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{id}}_{\phi_{x_k}}^{\phi_{x_0}}(x_0) \circ \Theta^\pm_{\phi_{x_k},\phi_{x_k}}( x_k,x_0 ) \circ \ldots \operatorname{\mathrm{id}}_{\phi_{x_1}}^{\phi_{x_2}}(x_2)\\ &\quad\circ \Theta^\pm_{\phi_{x_1},\phi_{x_1}} ( x_1,x_2 ) \circ \operatorname{\mathrm{id}}_{\phi_{x_0}}^{\phi_{x_1}}(x_1) \circ \Theta^\pm_{\phi_{x_0},\phi_{x_0}}( x_0,x_1 ), \end{align*} $$
where we can freely assume that each consecutive pair
![]() $x_i, x_{i+1}$
has a common trivialization
$x_i, x_{i+1}$
has a common trivialization
![]() $\phi _{x_i}$
for which
$\phi _{x_i}$
for which
![]() $B_\epsilon (x_i),B_\epsilon (x_{i+1}) \subset V_{x_i}$
; this is true up to refining the sequence (Figure 2). Suppose, moreover, that we have chosen
$B_\epsilon (x_i),B_\epsilon (x_{i+1}) \subset V_{x_i}$
; this is true up to refining the sequence (Figure 2). Suppose, moreover, that we have chosen
![]() $\phi _{x_0} = \phi _x$
.
$\phi _{x_0} = \phi _x$
.

Figure 2 A refined stable–unstable sequence
![]() $x_0, x_1, \ldots , x_k, x_{k+1} = x_0$
. Any stable–unstable sequence can be refined so that for each
$x_0, x_1, \ldots , x_k, x_{k+1} = x_0$
. Any stable–unstable sequence can be refined so that for each
![]() $0 \leq n \leq k$
, there is a trivialization
$0 \leq n \leq k$
, there is a trivialization
![]() $\phi _{x_n}$
over a chart
$\phi _{x_n}$
over a chart
![]() $V_{x_n}$
containing both
$V_{x_n}$
containing both
![]() $x_n$
and
$x_n$
and
![]() $x_{n+1}$
. This refinement has the same total holonomy.
$x_{n+1}$
. This refinement has the same total holonomy.
We would like to now invoke Proposition 4.6 and Lemmas 4.9 and 4.10 to show that
 $\mathfrak h^{\phi _x}_\epsilon (x)$
is
$\mathfrak h^{\phi _x}_\epsilon (x)$
is
![]() $\operatorname {\mathrm {Ad}}_g$
-invariant for the g corresponding to the total holonomy along this sequence. The
$\operatorname {\mathrm {Ad}}_g$
-invariant for the g corresponding to the total holonomy along this sequence. The
![]() $x_i$
we have chosen, however, may fail to be forwards- or backwards-recurrent as necessary. However, note that
$x_i$
we have chosen, however, may fail to be forwards- or backwards-recurrent as necessary. However, note that
 $\operatorname {\mathrm {id}}_{\phi _{x_i}}^{\phi _{x_{i+1}}}(\cdot )$
,
$\operatorname {\mathrm {id}}_{\phi _{x_i}}^{\phi _{x_{i+1}}}(\cdot )$
,
 $\Theta ^+_{\phi _{x_i},\phi _{x_i}}(\cdot ,\cdot )$
and
$\Theta ^+_{\phi _{x_i},\phi _{x_i}}(\cdot ,\cdot )$
and
 $\Theta ^-_{\phi _{x_i},\phi _{x_i}}(\cdot ,\cdot )$
are all locally continuous in all of their arguments. As bi-recurrent points are dense in N, given any
$\Theta ^-_{\phi _{x_i},\phi _{x_i}}(\cdot ,\cdot )$
are all locally continuous in all of their arguments. As bi-recurrent points are dense in N, given any
![]() $\delta> 0$
, we can find a sequence of bi-recurrent points
$\delta> 0$
, we can find a sequence of bi-recurrent points
 $x^{\prime }_0, x^{\prime }_1, \ldots , x^{\prime }_k, x^{\prime }_{k+1} = x^{\prime }_0$
near
$x^{\prime }_0, x^{\prime }_1, \ldots , x^{\prime }_k, x^{\prime }_{k+1} = x^{\prime }_0$
near
![]() $x_0, x_1, \ldots , x_k, x_{k+1} = x_0$
with
$x_0, x_1, \ldots , x_k, x_{k+1} = x_0$
with
![]() $x^{\prime }_0 = x$
whose total holonomy
$x^{\prime }_0 = x$
whose total holonomy
![]() $g'$
is given by
$g'$
is given by
 $$ \begin{align*} &\operatorname{\mathrm{id}}_{\phi_{x_k}}^{\phi_{x_0}}(x^{\prime}_0) \circ \Theta^\pm_{\phi_{x_k},\phi_{x_k}}( x^{\prime}_k,x^{\prime}_0 ) \circ \cdots \circ \operatorname{\mathrm{id}}_{\phi_{x_1}}^{\phi_{x_2}}(x^{\prime}_2)\\ &\quad\circ \Theta^\pm_{\phi_{x_1},\phi_{x_1}} ( x^{\prime}_1,x^{\prime}_2 ) \circ \operatorname{\mathrm{id}}_{\phi_{x_0}}^{\phi_{x_1}}(x^{\prime}_1) \circ \Theta^\pm_{\phi_{x_0},\phi_{x_0}}( x^{\prime}_0,x^{\prime}_1 ) \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{id}}_{\phi_{x_k}}^{\phi_{x_0}}(x^{\prime}_0) \circ \Theta^\pm_{\phi_{x_k},\phi_{x_k}}( x^{\prime}_k,x^{\prime}_0 ) \circ \cdots \circ \operatorname{\mathrm{id}}_{\phi_{x_1}}^{\phi_{x_2}}(x^{\prime}_2)\\ &\quad\circ \Theta^\pm_{\phi_{x_1},\phi_{x_1}} ( x^{\prime}_1,x^{\prime}_2 ) \circ \operatorname{\mathrm{id}}_{\phi_{x_0}}^{\phi_{x_1}}(x^{\prime}_1) \circ \Theta^\pm_{\phi_{x_0},\phi_{x_0}}( x^{\prime}_0,x^{\prime}_1 ) \end{align*} $$
so that we have
![]() $d_G(g',g) < \delta $
. As each
$d_G(g',g) < \delta $
. As each
![]() $x^{\prime }_i$
is bi-recurrent, successive applications of Proposition 4.6 and Lemmas 4.9 and 4.10 show that we have
$x^{\prime }_i$
is bi-recurrent, successive applications of Proposition 4.6 and Lemmas 4.9 and 4.10 show that we have
 $$ \begin{align*} \mathfrak h_\epsilon^{\phi_x}(x) = \operatorname{\mathrm{Ad}}_{g'}( \mathfrak h_\epsilon^{\phi_x}(x) ) \end{align*} $$
$$ \begin{align*} \mathfrak h_\epsilon^{\phi_x}(x) = \operatorname{\mathrm{Ad}}_{g'}( \mathfrak h_\epsilon^{\phi_x}(x) ) \end{align*} $$
for
![]() $g'$
arbitrarily close to G. As
$g'$
arbitrarily close to G. As
![]() $\operatorname {\mathrm {Ad}}_{g'}$
is continuous in
$\operatorname {\mathrm {Ad}}_{g'}$
is continuous in
![]() $g'$
, we then obtain
$g'$
, we then obtain
 $$ \begin{align*} \mathfrak h_\epsilon^{\phi_x}(x) = \operatorname{\mathrm{Ad}}_{g}( \mathfrak h_\epsilon^{\phi_x}(x) ) \end{align*} $$
$$ \begin{align*} \mathfrak h_\epsilon^{\phi_x}(x) = \operatorname{\mathrm{Ad}}_{g}( \mathfrak h_\epsilon^{\phi_x}(x) ) \end{align*} $$
as desired.
It is worth remarking that, under our standing assumption that trivializations must have constant projection to F along strong stable leaves of
![]() $f_t$
, the stable holonomies
$f_t$
, the stable holonomies
 $\Theta ^-_{\phi _{x_i},\phi _{x_i}}(x_i,x_{i+1})$
that appeared in the preceding proof must all be trivial.
$\Theta ^-_{\phi _{x_i},\phi _{x_i}}(x_i,x_{i+1})$
that appeared in the preceding proof must all be trivial.
We want to show that
![]() $\mathfrak h_\epsilon ^*(\cdot )$
is equal to the full Lie algebra
$\mathfrak h_\epsilon ^*(\cdot )$
is equal to the full Lie algebra
![]() $\mathfrak g$
, and the local G-accessibility of the extension will be crucial at this point. In fact, with Theorem 4.11, we can show that local G-accessibility at a point
$\mathfrak g$
, and the local G-accessibility of the extension will be crucial at this point. In fact, with Theorem 4.11, we can show that local G-accessibility at a point
![]() $x \in N$
is roughly equivalent to having
$x \in N$
is roughly equivalent to having
 $\mathfrak h_\epsilon ^\phi (x) = \mathfrak g$
.
$\mathfrak h_\epsilon ^\phi (x) = \mathfrak g$
.
Theorem 4.12. Fix
![]() $\epsilon> 0$
,
$\epsilon> 0$
,
![]() $x \in N$
and a trivialization
$x \in N$
and a trivialization
![]() $\phi _x$
defined over
$\phi _x$
defined over
![]() $V_x \subset N$
for which we have
$V_x \subset N$
for which we have
![]() $B_{3\epsilon }(x) \subset V_x$
. Moreover, suppose that
$B_{3\epsilon }(x) \subset V_x$
. Moreover, suppose that
 $\mathfrak h_\epsilon ^{\phi _x}(\cdot )$
is continuous and has maximal dimension on
$\mathfrak h_\epsilon ^{\phi _x}(\cdot )$
is continuous and has maximal dimension on
![]() $B_{3\epsilon }(x)$
, and that the forwards orbit of x under
$B_{3\epsilon }(x)$
, and that the forwards orbit of x under
![]() $g_t$
is dense in
$g_t$
is dense in
![]() $B_{2\epsilon }(x)$
. If
$B_{2\epsilon }(x)$
. If
![]() $f_t$
is locally G-accessible at x, then
$f_t$
is locally G-accessible at x, then
 $\mathfrak h_\epsilon ^{\phi _x}(x) = \mathfrak g$
.
$\mathfrak h_\epsilon ^{\phi _x}(x) = \mathfrak g$
.
Proof. Without loss of generality, suppose that we have chosen
![]() $\phi _x$
so that
$\phi _x$
so that
 $\Theta ^+_{\phi _x,\phi _x}(x,u)$
is trivial for all
$\Theta ^+_{\phi _x,\phi _x}(x,u)$
is trivial for all
![]() $u \in (W^{su}_{g_t}(x) \cap B_{2\epsilon }(x) )^\circ $
, and so that
$u \in (W^{su}_{g_t}(x) \cap B_{2\epsilon }(x) )^\circ $
, and so that
![]() $\Theta ^-_{\phi _x,\phi _x}(s_1,s_2)$
is trivial whenever
$\Theta ^-_{\phi _x,\phi _x}(s_1,s_2)$
is trivial whenever
![]() $s_1$
and
$s_1$
and
![]() $s_2$
lie on the same (local) leaf of the strong stable foliation of
$s_2$
lie on the same (local) leaf of the strong stable foliation of
![]() $g_t$
in
$g_t$
in
![]() $B_{2\epsilon }(x)$
.
$B_{2\epsilon }(x)$
.
We write
 $\mathfrak h := \mathfrak h_\epsilon ^{\phi _x}(x)$
and suppose for the sake of contradiction that
$\mathfrak h := \mathfrak h_\epsilon ^{\phi _x}(x)$
and suppose for the sake of contradiction that
![]() $\mathfrak h \subsetneq \mathfrak g$
is a proper subalgebra. By Proposition 4.9 and our choice of
$\mathfrak h \subsetneq \mathfrak g$
is a proper subalgebra. By Proposition 4.9 and our choice of
![]() $\phi _x$
, we must have
$\phi _x$
, we must have
 $\mathfrak h_\epsilon ^{\phi _x}(u) = \mathfrak h$
for all
$\mathfrak h_\epsilon ^{\phi _x}(u) = \mathfrak h$
for all
![]() $u \in B_\epsilon (x)$
lying on the local leaf through x of the strong unstable foliation of
$u \in B_\epsilon (x)$
lying on the local leaf through x of the strong unstable foliation of
![]() $g_t$
. Hence, for any
$g_t$
. Hence, for any
![]() $u_1 \in B_\epsilon (x)$
, each vector
$u_1 \in B_\epsilon (x)$
, each vector
 $X_{w'}^{\phi _x}(u_1)$
used in the definition of
$X_{w'}^{\phi _x}(u_1)$
used in the definition of
 $\mathfrak h_\epsilon ^{\phi _x}(u)$
must lie in the Lie algebra
$\mathfrak h_\epsilon ^{\phi _x}(u)$
must lie in the Lie algebra
![]() $\mathfrak h$
. Integrating this, we see that the unstable holonomies
$\mathfrak h$
. Integrating this, we see that the unstable holonomies
 $\Theta ^+_{\phi _x,\phi _x}(u_1,u_2)$
are constrained to
$\Theta ^+_{\phi _x,\phi _x}(u_1,u_2)$
are constrained to
![]() $\exp (\mathfrak h)$
for all
$\exp (\mathfrak h)$
for all
![]() $u_1,u_2 \in B_\epsilon (x)$
that lie on the same local leaf of the strong unstable foliation of
$u_1,u_2 \in B_\epsilon (x)$
that lie on the same local leaf of the strong unstable foliation of
![]() $g_t$
.
$g_t$
.
Now, consider
![]() $H := \exp (\mathfrak h)$
and consider an element
$H := \exp (\mathfrak h)$
and consider an element
![]() $g \in G \setminus H$
that lies in the complement. By our construction of
$g \in G \setminus H$
that lies in the complement. By our construction of
![]() $\phi _x$
, all unstable holonomies are constrained to H and all stable holonomies are trivial; hence, no local sequence of stable and unstable holonomies along a sequence of points
$\phi _x$
, all unstable holonomies are constrained to H and all stable holonomies are trivial; hence, no local sequence of stable and unstable holonomies along a sequence of points
![]() $x, x_1, x_2, \ldots x_k, x$
lying in
$x, x_1, x_2, \ldots x_k, x$
lying in
![]() $B_\epsilon (x)$
can result in a total holonomy of g. Moreover, because
$B_\epsilon (x)$
can result in a total holonomy of g. Moreover, because
![]() $\mathfrak h$
is an ideal by Theorem 4.11, H is a normal subgroup of G; hence, we cannot obtain a total holonomy of g for any choice of trivialization. As
$\mathfrak h$
is an ideal by Theorem 4.11, H is a normal subgroup of G; hence, we cannot obtain a total holonomy of g for any choice of trivialization. As
![]() $f_t$
is locally G-accessible at x, this is a contradiction.
$f_t$
is locally G-accessible at x, this is a contradiction.
It is worth noting that accessibility within a single, fixed trivialization
![]() $\phi _x$
at a given
$\phi _x$
at a given
![]() $x \in N$
is vital here. Indeed, if we only had global rather than local accessibility, the unstable holonomies could be constrained to
$x \in N$
is vital here. Indeed, if we only had global rather than local accessibility, the unstable holonomies could be constrained to
![]() $\exp (\mathfrak h)$
as in the proof of Theorem 4.12 without any contradiction, because the transition functions between different trivialization charts need not act by
$\exp (\mathfrak h)$
as in the proof of Theorem 4.12 without any contradiction, because the transition functions between different trivialization charts need not act by
![]() $\exp (\mathfrak h)$
.
$\exp (\mathfrak h)$
.
With Theorem 4.12, all that remains in this section is to verify that this translates properly into the symbolic model we are working with. In principle, the difficulty is that unstable leaves for the discrete dynamical system
![]() $(R, \mathcal P)$
are typically not unstable leaves for
$(R, \mathcal P)$
are typically not unstable leaves for
![]() $g_t$
; fortunately, our choice of trivializations will circumvent almost all of these problems.
$g_t$
; fortunately, our choice of trivializations will circumvent almost all of these problems.
Recall that
![]() $(R, \mathcal P)$
is a Markov partition associated with
$(R, \mathcal P)$
is a Markov partition associated with
![]() $g_t$
, which descends to a
$g_t$
, which descends to a
![]() $C^1$
expanding model
$C^1$
expanding model
![]() $(U, \sigma )$
by projecting along leaves of the strong stable foliation of
$(U, \sigma )$
by projecting along leaves of the strong stable foliation of
![]() $g_t$
. We want to define unstable holonomies entirely within the symbolic model; a natural candidate for a definition comes from Proposition 4.1. For everything that follows, we assume that each
$g_t$
. We want to define unstable holonomies entirely within the symbolic model; a natural candidate for a definition comes from Proposition 4.1. For everything that follows, we assume that each
![]() $R_i \subset N$
has been assigned a fixed trivialization
$R_i \subset N$
has been assigned a fixed trivialization
![]() $\phi _i$
defined on a neighbourhood
$\phi _i$
defined on a neighbourhood
![]() $B_\epsilon (R_i)$
, with the property that
$B_\epsilon (R_i)$
, with the property that
![]() $\phi _i$
has constant projection to F along each leaf of the strong stable foliation of
$\phi _i$
has constant projection to F along each leaf of the strong stable foliation of
![]() $f_t$
and each flowline of
$f_t$
and each flowline of
![]() $f_t$
. By choosing and fixing trivializations at each point in R, we no longer need to specify which trivialization we are using, at least when dealing with the symbolic model.
$f_t$
. By choosing and fixing trivializations at each point in R, we no longer need to specify which trivialization we are using, at least when dealing with the symbolic model.
Definition 4.4. Fix
![]() $x \in R$
and
$x \in R$
and
![]() $y \in W^{su}_{\mathcal P}(x)$
. The symbolic unstable holonomy
$y \in W^{su}_{\mathcal P}(x)$
. The symbolic unstable holonomy
 $\Theta ^+_{\mathrm {symb}}(x,y)$
is defined to be the limit
$\Theta ^+_{\mathrm {symb}}(x,y)$
is defined to be the limit
 $$ \begin{align*} \Theta^+_{\mathrm{symb}}(x,y) := \lim_{n \to \infty} \operatorname{\mathrm{Hol}}^{(n)}(\mathcal P^{-n}(y)) ( \operatorname{\mathrm{Hol}}^{(n)}( \mathcal P^{-n}(x) ) )^{-1}, \end{align*} $$
$$ \begin{align*} \Theta^+_{\mathrm{symb}}(x,y) := \lim_{n \to \infty} \operatorname{\mathrm{Hol}}^{(n)}(\mathcal P^{-n}(y)) ( \operatorname{\mathrm{Hol}}^{(n)}( \mathcal P^{-n}(x) ) )^{-1}, \end{align*} $$
where we write
for the nth holonomy under the Poincaré return map.
It is straightforward to verify that this limit exists. Moreover, our choice of trivializations ensures that the symbolic unstable holonomies agree with the appropriate (non-symbolic) unstable holonomies.
Proposition 4.13. Fix
![]() $x \in R$
and
$x \in R$
and
![]() $y \in W^{su}_{\mathcal P}(x)$
. There is a (possibly negative) t so that
$y \in W^{su}_{\mathcal P}(x)$
. There is a (possibly negative) t so that
![]() $g_t(y) \in W^{su}_{g_t}(x)$
for which we have
$g_t(y) \in W^{su}_{g_t}(x)$
for which we have
 $$ \begin{align*} \Theta^+_{\mathrm{symb}}(x,y) = \Theta^+_{\phi_x,\phi_y}(x,g_t(y)), \end{align*} $$
$$ \begin{align*} \Theta^+_{\mathrm{symb}}(x,y) = \Theta^+_{\phi_x,\phi_y}(x,g_t(y)), \end{align*} $$
assuming x and y are sufficiently close, where
![]() $\phi _x,\phi _y$
are trivializations corresponding to the respective parts of the Markov partition.
$\phi _x,\phi _y$
are trivializations corresponding to the respective parts of the Markov partition.
Proof. The existence of such a t satisfying
![]() $|t| < \tau (y), \tau ( \mathcal P^{-1}(y) )$
follows immediately from the construction of the Markov partition
$|t| < \tau (y), \tau ( \mathcal P^{-1}(y) )$
follows immediately from the construction of the Markov partition
![]() $(R, \mathcal P)$
. We then clearly have
$(R, \mathcal P)$
. We then clearly have
 $$ \begin{align*} \Theta^+_{\mathrm{symb}}(x,y) = \operatorname{\mathrm{Hol}}_{\phi_y}^{\phi_y}(g_t(y),y,-t) \circ \Theta^+_{\phi_x,\phi_y}(x, g_t(y)) \end{align*} $$
$$ \begin{align*} \Theta^+_{\mathrm{symb}}(x,y) = \operatorname{\mathrm{Hol}}_{\phi_y}^{\phi_y}(g_t(y),y,-t) \circ \Theta^+_{\phi_x,\phi_y}(x, g_t(y)) \end{align*} $$
by Proposition 4.1 and Definition 4.4. By our choice of trivialization and the fact that t does not exceed the return time of y,
 $\operatorname {\mathrm {Hol}}_{\phi _y}^{\phi _y}(g_t(y),y,-t)$
is the identity in G, as desired.
$\operatorname {\mathrm {Hol}}_{\phi _y}^{\phi _y}(g_t(y),y,-t)$
is the identity in G, as desired.
Now, we can analogously define the symbolic infinitesimal transitivity group.
Definition 4.5. Fix
![]() $x \in U_i$
and a vector
$x \in U_i$
and a vector
![]() $w \in T^1_xU_i$
. We define the symbolic infinitesimal holonomy at x in the direction of w to be the element
$w \in T^1_xU_i$
. We define the symbolic infinitesimal holonomy at x in the direction of w to be the element

of the Lie algebra
![]() $\mathfrak g$
of G. The symbolic infinitesimal transitivity group at x is defined to be the linear span
$\mathfrak g$
of G. The symbolic infinitesimal transitivity group at x is defined to be the linear span
 $$ \begin{align*} \mathfrak h_{\mathrm{symb}}(x) := \operatorname*{\mathrm{span}}_{s,s',w} ( X_{w'}([x,s']) - X_w([x,s]) ), \end{align*} $$
$$ \begin{align*} \mathfrak h_{\mathrm{symb}}(x) := \operatorname*{\mathrm{span}}_{s,s',w} ( X_{w'}([x,s']) - X_w([x,s]) ), \end{align*} $$
where we take the span over
![]() $s,s' \in S_i$
,
$s,s' \in S_i$
,
![]() $w \in T_x^1U_i$
and let
$w \in T_x^1U_i$
and let
![]() $w'$
be the projection of w to
$w'$
be the projection of w to
![]() $[x,s']$
via centre-stable leaves followed by the flow.
$[x,s']$
via centre-stable leaves followed by the flow.
With very little work, we can now prove the following result.
Theorem 4.14. Fix a bi-recurrent
![]() $x \in U_i$
at which
$x \in U_i$
at which
![]() $\dim \mathfrak h_\epsilon (x)$
is maximal, and suppose that
$\dim \mathfrak h_\epsilon (x)$
is maximal, and suppose that
![]() $f_t$
is G-accessible. Then
$f_t$
is G-accessible. Then
![]() $\mathfrak h_{\mathrm {symb}}(x) = \mathfrak g$
.
$\mathfrak h_{\mathrm {symb}}(x) = \mathfrak g$
.
Proof. By Proposition 4.13, the unstable holonomies used in Definitions 4.3 and 4.5 are the same. Hence, the regular and symbolic transitivity groups agree, and so by Theorem 4.11, we have
![]() $\mathfrak h_{\mathrm {symb}}(x) = \mathfrak g$
.
$\mathfrak h_{\mathrm {symb}}(x) = \mathfrak g$
.
This is almost the result we want, but we need to use some Lie theory to extract the explicit estimates that we use in the next section. We want to phrase this in terms of
![]() $\sigma $
, which means minor notational changes in the preceding theorems. Recall that
$\sigma $
, which means minor notational changes in the preceding theorems. Recall that
![]() $\sigma \colon U \to U$
is not actually invertible; to make sense of the inverse, we must choose branches of
$\sigma \colon U \to U$
is not actually invertible; to make sense of the inverse, we must choose branches of
![]() $\sigma ^{-n}$
locally.
$\sigma ^{-n}$
locally.
Definition 4.6. A consistent past for
![]() $u \in U_i$
is a sequence of maps
$u \in U_i$
is a sequence of maps
 $\{v^{(n)} \colon U_i \to U_{j(n)} \mid n \geq 0\}$
where
$\{v^{(n)} \colon U_i \to U_{j(n)} \mid n \geq 0\}$
where
 and
and
![]() $\sigma \circ v^{(n)} = v^{(n-1)}$
.
$\sigma \circ v^{(n)} = v^{(n-1)}$
.
Remark 4.15. A consistent past for
![]() $u \in U_i$
corresponds exactly to a choice of stable element
$u \in U_i$
corresponds exactly to a choice of stable element
![]() $s \in S_i$
: we can recover the maps
$s \in S_i$
: we can recover the maps
![]() $\{ v^{(n)} \}$
by projecting the Poincaré return map
$\{ v^{(n)} \}$
by projecting the Poincaré return map
![]() $\mathcal P^{(-n)}$
along leaves of the strong stable foliation.
$\mathcal P^{(-n)}$
along leaves of the strong stable foliation.
Finally, we can establish the main estimate; this is fundamentally the same estimate as [Reference Dolgopyat12, Lemma 3.17] and [Reference Sharp17, Lemma 5.5], the primary difference being in the analysis of the infinitesimal transitivity group needed to arrive at it.
Theorem 4.16. Let
![]() $\rho $
be an isotypic component of the representation of G on
$\rho $
be an isotypic component of the representation of G on
![]() $L^2(G)$
. There is an open subset
$L^2(G)$
. There is an open subset
![]() $U_{lni} \subset U$
and constants
$U_{lni} \subset U$
and constants
![]() $\epsilon , \delta , n_0> 0$
so that, for any
$\epsilon , \delta , n_0> 0$
so that, for any
![]() $x \in U_{lni}$
and any
$x \in U_{lni}$
and any
![]() $\varphi \in C^1(U, V^\rho )$
, there are consistent pasts
$\varphi \in C^1(U, V^\rho )$
, there are consistent pasts
 $v_1 = \{v_1^{(n)}\}$
and
$v_1 = \{v_1^{(n)}\}$
and
 $v_2 = \{v_2^{(n)}\}$
defined near x and a
$v_2 = \{v_2^{(n)}\}$
defined near x and a
![]() $C^1$
vector field
$C^1$
vector field
![]() $w \colon U_{lni} \to T^1U_{lni}$
satisfying
$w \colon U_{lni} \to T^1U_{lni}$
satisfying
 $$ \begin{align*} \| (d\rho( X_{w(u),v_1}^{\mathrm{symb}}(u) - X_{w(u),v_2}^{\mathrm{symb}}(u) ))(\varphi(u)) \|_{L^2(G)} \geq \epsilon \|\rho\| \end{align*} $$
$$ \begin{align*} \| (d\rho( X_{w(u),v_1}^{\mathrm{symb}}(u) - X_{w(u),v_2}^{\mathrm{symb}}(u) ))(\varphi(u)) \|_{L^2(G)} \geq \epsilon \|\rho\| \end{align*} $$
for all
![]() $u \in B_\delta (x)$
.
$u \in B_\delta (x)$
.
Proof. By definition, we have

for all
![]() $u \in B_\delta (x)$
. The derivatives of the terms in the sequence converge exponentially fast in n, so we can interchange the limit and the derivative to obtain
$u \in B_\delta (x)$
. The derivatives of the terms in the sequence converge exponentially fast in n, so we can interchange the limit and the derivative to obtain

for any consistent past
![]() $v_i$
. As the
$v_i$
. As the
 $X_{w(u),v_i}^{\mathrm {symb}} - X_{w(u),v_j}^{\mathrm {symb}}$
taken over pasts
$X_{w(u),v_i}^{\mathrm {symb}} - X_{w(u),v_j}^{\mathrm {symb}}$
taken over pasts
![]() $v_i, v_j$
and vectors w form a basis of
$v_i, v_j$
and vectors w form a basis of
![]() $\mathfrak g$
, there is a finite
$\mathfrak g$
, there is a finite
![]() $n_0$
so that the approximations
$n_0$
so that the approximations

can also be used to form a basis
 $X_{w(u),v_i^{(n_0)}}^{\mathrm {symb}}(x) - X_{w(u),v_j^{(n_0)}}^{\mathrm {symb}}(x)$
, taken again over pasts
$X_{w(u),v_i^{(n_0)}}^{\mathrm {symb}}(x) - X_{w(u),v_j^{(n_0)}}^{\mathrm {symb}}(x)$
, taken again over pasts
![]() $v_i, v_j$
and vectors w. Hence, we have a Casimir
$v_i, v_j$
and vectors w. Hence, we have a Casimir
 $$ \begin{align*} \Omega = \sum ( g_{ij} )^{-1} ( X_{w,v_i^{(n_0)}}^{\mathrm{symb}}(x) - X_{w,v_j^{(n_0)}}^{\mathrm{symb}}(x) ) ( X_{w,v_i^{(n_0)}}^{\mathrm{symb}}(x) - X_{w,v_j^{(n_0)}}^{\mathrm{symb}}(x) ) \end{align*} $$
$$ \begin{align*} \Omega = \sum ( g_{ij} )^{-1} ( X_{w,v_i^{(n_0)}}^{\mathrm{symb}}(x) - X_{w,v_j^{(n_0)}}^{\mathrm{symb}}(x) ) ( X_{w,v_i^{(n_0)}}^{\mathrm{symb}}(x) - X_{w,v_j^{(n_0)}}^{\mathrm{symb}}(x) ) \end{align*} $$
for some finite collection of pasts
![]() $v_i, v_j$
and a given vector w. This acts on
$v_i, v_j$
and a given vector w. This acts on
![]() $V^\rho $
by scalar multiplication by
$V^\rho $
by scalar multiplication by
![]() $\|\rho \|^2$
, and so we obtain
$\|\rho \|^2$
, and so we obtain
 $$ \begin{align*} d\rho\bigg(\sum (g_{ij})^{-1} ( X_{w,v_i^{(n_0)}}^{\mathrm{symb}}(x) - X_{w,v_j^{(n_0)}}^{\mathrm{symb}}(x) )^2\bigg)( \varphi(x) ) = \|\rho\|^2 \varphi(x) \end{align*} $$
$$ \begin{align*} d\rho\bigg(\sum (g_{ij})^{-1} ( X_{w,v_i^{(n_0)}}^{\mathrm{symb}}(x) - X_{w,v_j^{(n_0)}}^{\mathrm{symb}}(x) )^2\bigg)( \varphi(x) ) = \|\rho\|^2 \varphi(x) \end{align*} $$
for this collection of pasts, and the same vector w. Now, there is a uniform constant
![]() $\epsilon> 0$
, depending only on the
$\epsilon> 0$
, depending only on the
![]() $g_{ij}$
and
$g_{ij}$
and
![]() $\mathfrak g$
, so that
$\mathfrak g$
, so that
 $$ \begin{align*} \| d\rho( X_{w,v_i^{(n_0)}}^{\mathrm{symb}}(x) - X_{w,v_j^{(n_0)}}^{\mathrm{symb}}(x) ) ( \varphi(x) ) \|_{L^2(G)} \geq \epsilon \|\rho\| \varphi(x) \end{align*} $$
$$ \begin{align*} \| d\rho( X_{w,v_i^{(n_0)}}^{\mathrm{symb}}(x) - X_{w,v_j^{(n_0)}}^{\mathrm{symb}}(x) ) ( \varphi(x) ) \|_{L^2(G)} \geq \epsilon \|\rho\| \varphi(x) \end{align*} $$
for some choice of
![]() $v_i, v_j$
and w. As
$v_i, v_j$
and w. As
 $X_{w,v}^{\mathrm {symb}}(u)$
varies continuously in w and u, there is a neighbourhood
$X_{w,v}^{\mathrm {symb}}(u)$
varies continuously in w and u, there is a neighbourhood
![]() $B_\delta (x)$
of x in U and a
$B_\delta (x)$
of x in U and a
![]() $C^1$
vector field
$C^1$
vector field
![]() $w \colon B_\delta (x) \to T^1B_\delta (x)$
for which
$w \colon B_\delta (x) \to T^1B_\delta (x)$
for which
 $$ \begin{align*} \| d\rho( X_{w(u),v_i^{(n_0)}}^{\mathrm{symb}}(u) - X_{w(u),v_j^{(n_0)}}^{\mathrm{symb}}(u) ) ( \varphi(u) ) \|_{L^2(G)} \geq \frac \epsilon 2 \|\rho\| \varphi(u) \end{align*} $$
$$ \begin{align*} \| d\rho( X_{w(u),v_i^{(n_0)}}^{\mathrm{symb}}(u) - X_{w(u),v_j^{(n_0)}}^{\mathrm{symb}}(u) ) ( \varphi(u) ) \|_{L^2(G)} \geq \frac \epsilon 2 \|\rho\| \varphi(u) \end{align*} $$
holds for all
![]() $u \in B_\delta (x)$
, as desired.
$u \in B_\delta (x)$
, as desired.
5 Spectral bounds for
 $\mathcal L^n_{z,\rho }$
$\mathcal L^n_{z,\rho }$
In this section, we establish bounds for the twisted transfer operators
![]() $\mathcal L^n_{z,\rho }$
acting on
$\mathcal L^n_{z,\rho }$
acting on
![]() $C^1(U, V^\rho )$
with respect to the
$C^1(U, V^\rho )$
with respect to the
![]() $L^2(\nu ^u)$
-norm. The key ingredients are the local non-integrability estimate in Theorem 4.16, the diametric regularity of the measure
$L^2(\nu ^u)$
-norm. The key ingredients are the local non-integrability estimate in Theorem 4.16, the diametric regularity of the measure
![]() $\nu ^u$
and the
$\nu ^u$
and the
![]() $C^1$
regularity of
$C^1$
regularity of
![]() $\alpha _z$
from the definition of the transfer operators.
$\alpha _z$
from the definition of the transfer operators.
The strategy adopted in this section is by now classical, dating back to Dolgopyat in [Reference Dolgopyat11, Reference Dolgopyat12]; an account of this almost completely adapted to our setting was given by Winter in [Reference Sharp17]. The reader already familiar with these arguments should find few surprises in this section, but we feel it necessary to include them given their delicate nature and the minor differences in our contexts.
We begin by recalling the definition of the twisted transfer operator
 $$ \begin{align*} (\mathcal L^n_{z,\rho}\varphi)(u) := \sum_{\sigma^n(u')=u} e^{\alpha_z^{(n)}(u')} \rho( \operatorname{\mathrm{Hol}}^{(n)}(u') ) \varphi(u') \end{align*} $$
$$ \begin{align*} (\mathcal L^n_{z,\rho}\varphi)(u) := \sum_{\sigma^n(u')=u} e^{\alpha_z^{(n)}(u')} \rho( \operatorname{\mathrm{Hol}}^{(n)}(u') ) \varphi(u') \end{align*} $$
associated with an irreducible representation
![]() $\rho $
of G on
$\rho $
of G on
![]() $V^\rho \subset L^2(G)$
. For the trivial representation
$V^\rho \subset L^2(G)$
. For the trivial representation
![]() $\rho = 0$
, Dolgopyat [Reference Dolgopyat11] established contraction by using the uniform non-integrability of the strong stable and unstable foliations for
$\rho = 0$
, Dolgopyat [Reference Dolgopyat11] established contraction by using the uniform non-integrability of the strong stable and unstable foliations for
![]() $g_t$
to establish cancellation in the terms defining the transfer operator. In principle, the difficulty in obtaining contraction for
$g_t$
to establish cancellation in the terms defining the transfer operator. In principle, the difficulty in obtaining contraction for
![]() $\|\mathcal L^n_{z,\rho } \varphi \|_{L^2(\nu ^u)}$
as
$\|\mathcal L^n_{z,\rho } \varphi \|_{L^2(\nu ^u)}$
as
![]() $n \to \infty $
lies in the possibility that the rotation introduced by the action of
$n \to \infty $
lies in the possibility that the rotation introduced by the action of
![]() $\rho $
may ‘undo’ any cancellation between the vectors
$\rho $
may ‘undo’ any cancellation between the vectors
![]() $\varphi (u') \in V^\rho $
that we might obtain from the dynamics on the base, and that this may happen on a set of large measure.
$\varphi (u') \in V^\rho $
that we might obtain from the dynamics on the base, and that this may happen on a set of large measure.
The local non-integrability estimate provided by Theorem 4.16, however, suggests that we should typically be able to find
![]() $u_1', u_2'$
with
$u_1', u_2'$
with
![]() $\sigma ^n(u_1') = \sigma ^n(u_2') \in U_{lni}$
so that
$\sigma ^n(u_1') = \sigma ^n(u_2') \in U_{lni}$
so that
 $$ \begin{align*} \rho ( \operatorname{\mathrm{Hol}}^{(n)}(u_1') ) \varphi(u_1')\quad \text{and}\quad \rho ( \operatorname{\mathrm{Hol}}^{(n)}(u_2') ) \varphi(u_2') \end{align*} $$
$$ \begin{align*} \rho ( \operatorname{\mathrm{Hol}}^{(n)}(u_1') ) \varphi(u_1')\quad \text{and}\quad \rho ( \operatorname{\mathrm{Hol}}^{(n)}(u_2') ) \varphi(u_2') \end{align*} $$
are ‘uniformly’ non-parallel. The main argument in the section boils down to verifying that this can be accomplished on an adequately large set, with explicit uniformity estimates.
Throughout this section, we work with a fixed isotypic component
![]() $V^\rho $
of the regular representation of G on
$V^\rho $
of the regular representation of G on
![]() $L^2(G)$
. However, it is worth noting that most of the intermediate constants will fundamentally depend on
$L^2(G)$
. However, it is worth noting that most of the intermediate constants will fundamentally depend on
![]() $\rho $
, and keeping track of these dependencies is essential to obtaining a final bound in Theorem 5.7 that is independent of
$\rho $
, and keeping track of these dependencies is essential to obtaining a final bound in Theorem 5.7 that is independent of
![]() $\rho $
.
$\rho $
.
Though we need to deal with
![]() $\mathcal L^n_{z,\rho } \varphi $
for any
$\mathcal L^n_{z,\rho } \varphi $
for any
![]() $\varphi \in C^1(U, V^\rho )$
, it will be helpful to work instead with slightly more regular real-valued functions
$\varphi \in C^1(U, V^\rho )$
, it will be helpful to work instead with slightly more regular real-valued functions
![]() $\Phi \in C^1(U, \mathbb {R}^+)$
with bounded logarithmic derivative; in other words, we require
$\Phi \in C^1(U, \mathbb {R}^+)$
with bounded logarithmic derivative; in other words, we require
 $$ \begin{align*} \sup_{w \in T_u^1U} | ( d\Phi )_u(w) | &< C \Phi(u) \end{align*} $$
$$ \begin{align*} \sup_{w \in T_u^1U} | ( d\Phi )_u(w) | &< C \Phi(u) \end{align*} $$
for all
![]() $u \in U$
. We use
$u \in U$
. We use
![]() $\mathcal K_C$
to denote the class of such functions
$\mathcal K_C$
to denote the class of such functions
for any constant
![]() $C> 0$
.
$C> 0$
.
As
![]() $g_t$
is Anosov, the expansion rates of
$g_t$
is Anosov, the expansion rates of
![]() $g_t$
on U are bounded away from
$g_t$
on U are bounded away from
![]() $1$
. As the return times
$1$
. As the return times
![]() $\tau \colon R \to \mathbb {R}$
are bounded away from zero, the slowest expansion rates of
$\tau \colon R \to \mathbb {R}$
are bounded away from zero, the slowest expansion rates of
![]() $d\sigma ^n$
on U are therefore also bounded away from
$d\sigma ^n$
on U are therefore also bounded away from
![]() $1$
. For what follows, let
$1$
. For what follows, let
![]() $f \kappa ^n$
and
$f \kappa ^n$
and
![]() $b K^n$
with
$b K^n$
with
![]() $1 < \kappa < K$
be the slowest and fastest expansion rate of any unit vector in
$1 < \kappa < K$
be the slowest and fastest expansion rate of any unit vector in
![]() $T^1U$
under
$T^1U$
under
![]() $d\sigma ^n$
.
$d\sigma ^n$
.
We are interested in functions
![]() $\Phi \in \mathcal K_C$
with bounded logarithmic derivative because they can be used to control less-regular functions
$\Phi \in \mathcal K_C$
with bounded logarithmic derivative because they can be used to control less-regular functions
![]() $\varphi \in C^1(U, \mathbb {R})$
. The following lemma makes this precise, and is analogous to [Reference Dolgopyat11, Lemma 14] and [Reference Sharp17, Lemma 6.5].
$\varphi \in C^1(U, \mathbb {R})$
. The following lemma makes this precise, and is analogous to [Reference Dolgopyat11, Lemma 14] and [Reference Sharp17, Lemma 6.5].
Lemma 5.1. Fix
![]() $C> 0$
,
$C> 0$
,
![]() $\varphi \in C^1(U, V^\rho )$
and
$\varphi \in C^1(U, V^\rho )$
and
![]() $\Phi \in \mathcal K_C$
. There is a
$\Phi \in \mathcal K_C$
. There is a
![]() $\delta> 0$
so that, if
$\delta> 0$
so that, if
 $$ \begin{align*} \| \varphi(u) \|_{L^2(G)} &< \Phi(u),\\ \sup_{w \in T_u^1U} \| ( d\varphi )_u(w) \|_{L^2(G)} &< C \Phi(u) \end{align*} $$
$$ \begin{align*} \| \varphi(u) \|_{L^2(G)} &< \Phi(u),\\ \sup_{w \in T_u^1U} \| ( d\varphi )_u(w) \|_{L^2(G)} &< C \Phi(u) \end{align*} $$
for all
![]() $u \in U$
, then for any
$u \in U$
, then for any
![]() $u_0 \in U$
,
$u_0 \in U$
,
 $$ \begin{align*} {\| \varphi(v^{(n)}(u)) \|_{L^2(G)}} &\leq \tfrac 3 4 {\Phi(v^{(n)}(u))} \end{align*} $$
$$ \begin{align*} {\| \varphi(v^{(n)}(u)) \|_{L^2(G)}} &\leq \tfrac 3 4 {\Phi(v^{(n)}(u))} \end{align*} $$
or
 $$ \begin{align*} {\| \varphi(v^{(n)}(u)) \|_{L^2(G)}}&\geq \tfrac 1 4{\Phi(v^{(n)}(u))} \end{align*} $$
$$ \begin{align*} {\| \varphi(v^{(n)}(u)) \|_{L^2(G)}}&\geq \tfrac 1 4{\Phi(v^{(n)}(u))} \end{align*} $$
for all
![]() $u \in B_\delta (u_0)$
, each
$u \in B_\delta (u_0)$
, each
![]() $n> 0$
and each consistent past
$n> 0$
and each consistent past
![]() $v = \{ v^{(n)} \}$
defined near
$v = \{ v^{(n)} \}$
defined near
![]() $u_0$
. Moreover, for any
$u_0$
. Moreover, for any
![]() $u_0 \in U$
,
$u_0 \in U$
,
for all
![]() $x, y \in B_\delta (u_0)$
. The choice of constant
$x, y \in B_\delta (u_0)$
. The choice of constant
![]() $\delta> 0$
can be made so that we have
$\delta> 0$
can be made so that we have
![]() $\delta C = A$
for some uniform constant A, which does not depend on
$\delta C = A$
for some uniform constant A, which does not depend on
![]() $\rho $
,
$\rho $
,
![]() $\Phi $
,
$\Phi $
,
![]() $\varphi $
,
$\varphi $
,
![]() $u_0$
, v or n.
$u_0$
, v or n.
Proof. As we chose
![]() $\Phi \in \mathcal K_C$
,
$\Phi \in \mathcal K_C$
,
![]() $\log \Phi $
is C-Lipschitz and we therefore have
$\log \Phi $
is C-Lipschitz and we therefore have
 $$ \begin{align*} | \log ( \Phi(v^{(n)}(y)) ) - \log ( \Phi( v^{(n)}(x) ) ) | &\leq \frac C {f\kappa^n} d(x,y)\\ &\leq \frac C f d(x,y) \end{align*} $$
$$ \begin{align*} | \log ( \Phi(v^{(n)}(y)) ) - \log ( \Phi( v^{(n)}(x) ) ) | &\leq \frac C {f\kappa^n} d(x,y)\\ &\leq \frac C f d(x,y) \end{align*} $$
for any
![]() $x,y \in U$
. Exponentiating both sides, this means
$x,y \in U$
. Exponentiating both sides, this means
for any
![]() $x,y \in U$
. Now, suppose that
$x,y \in U$
. Now, suppose that
![]() $d(x,y) \leq 2\delta $
for some
$d(x,y) \leq 2\delta $
for some
![]() $\delta> 0$
, and fix a unit speed path
$\delta> 0$
, and fix a unit speed path
![]() $\gamma \colon [0,2\delta ] \to U_0$
with
$\gamma \colon [0,2\delta ] \to U_0$
with
![]() $\gamma (0) = y$
and
$\gamma (0) = y$
and
![]() $\gamma (2\delta ) = x$
. We then have
$\gamma (2\delta ) = x$
. We then have
 $$ \begin{align*} | \|\varphi(v^{(n)}(x)) |_{L^2(G)} - \|\varphi( v^{(n)}(y) ) \|_{L^2(G)} | &\leq \int_0^{2\delta} |\langle \operatorname{\mathrm{grad}}( \varphi \circ v^{(n)} )(\gamma(t)), \gamma'(t) \rangle_{T^1N} | \, dt\\ &\leq \frac C {f\kappa^n} \int_0^{2\delta} ( \Phi \circ v^{(n)} )(\gamma(t)) \, dt\\ &\leq \frac C {f \kappa^n} {2\delta} e^{( C /{f\kappa^n}) d(x,y)} \Phi( v^{(n)}(y) )\\ &\leq \frac C {f} \delta e^{(C/{f}) 2\delta} \Phi( v^{(n)}(y) ) \end{align*} $$
$$ \begin{align*} | \|\varphi(v^{(n)}(x)) |_{L^2(G)} - \|\varphi( v^{(n)}(y) ) \|_{L^2(G)} | &\leq \int_0^{2\delta} |\langle \operatorname{\mathrm{grad}}( \varphi \circ v^{(n)} )(\gamma(t)), \gamma'(t) \rangle_{T^1N} | \, dt\\ &\leq \frac C {f\kappa^n} \int_0^{2\delta} ( \Phi \circ v^{(n)} )(\gamma(t)) \, dt\\ &\leq \frac C {f \kappa^n} {2\delta} e^{( C /{f\kappa^n}) d(x,y)} \Phi( v^{(n)}(y) )\\ &\leq \frac C {f} \delta e^{(C/{f}) 2\delta} \Phi( v^{(n)}(y) ) \end{align*} $$
by the fundamental theorem of calculus and our bounds on
![]() $\varphi $
. Fix
$\varphi $
. Fix
![]() $\delta $
small enough to ensure
$\delta $
small enough to ensure
 $$ \begin{align*} \frac C {f} 2\delta e^{ (C/f) 2\delta} \leq \frac 1 8 \end{align*} $$
$$ \begin{align*} \frac C {f} 2\delta e^{ (C/f) 2\delta} \leq \frac 1 8 \end{align*} $$
and
hold simultaneously; note that we really only require that
![]() $C \delta $
is sufficiently small, and so
$C \delta $
is sufficiently small, and so
![]() $\delta $
can be chosen inversely proportional to C. We therefore have
$\delta $
can be chosen inversely proportional to C. We therefore have
and
 $$ \begin{align} \| \varphi( v^{(n)}(x) ) \|_{L^2(G)} \leq \| \varphi( v^{(n)}(y) ) \|_{L^2(G)} + \tfrac 1 8 \Phi( v^{(n)}(y) ) \end{align} $$
$$ \begin{align} \| \varphi( v^{(n)}(x) ) \|_{L^2(G)} \leq \| \varphi( v^{(n)}(y) ) \|_{L^2(G)} + \tfrac 1 8 \Phi( v^{(n)}(y) ) \end{align} $$
whenever
![]() $d(x,y) < 2\delta $
. To conclude, suppose that we had
$d(x,y) < 2\delta $
. To conclude, suppose that we had
 $$ \begin{align*} {\| \varphi(v^{(n)}(y)) \|_{L^2(G)}} \leq \tfrac 1 4{\Phi(v^{(n)}(y))} \end{align*} $$
$$ \begin{align*} {\| \varphi(v^{(n)}(y)) \|_{L^2(G)}} \leq \tfrac 1 4{\Phi(v^{(n)}(y))} \end{align*} $$
at some
![]() $y \in B_{\delta }(u_0)$
, for a given
$y \in B_{\delta }(u_0)$
, for a given
![]() $u_0 \in U$
and n. Then by (5.3) and (5.2), we must have
$u_0 \in U$
and n. Then by (5.3) and (5.2), we must have
 $$ \begin{align*} \| \varphi( v^{(n)}(x) ) \|_{L^2(G)} &\leq \tfrac 1 4 \Phi( v^{(n)}(y) ) + \tfrac 1 8 \Phi( v^{(n)}(y) )\\[3pt] &\leq \tfrac 2 4 \Phi( v^{(n)}(x) ) + \tfrac 2 8 \Phi( v^{(n)}(x) )\\[3pt] &\leq \tfrac 3 4 \Phi( v^{(n)}(x) ) \end{align*} $$
$$ \begin{align*} \| \varphi( v^{(n)}(x) ) \|_{L^2(G)} &\leq \tfrac 1 4 \Phi( v^{(n)}(y) ) + \tfrac 1 8 \Phi( v^{(n)}(y) )\\[3pt] &\leq \tfrac 2 4 \Phi( v^{(n)}(x) ) + \tfrac 2 8 \Phi( v^{(n)}(x) )\\[3pt] &\leq \tfrac 3 4 \Phi( v^{(n)}(x) ) \end{align*} $$
for any
![]() $x \in B_{\delta }(u_0)$
, as desired.
$x \in B_{\delta }(u_0)$
, as desired.
Lemma 5.2. Fix
![]() $C> 0$
,
$C> 0$
,
![]() $\varphi \in C^1(U, V^\rho )$
and
$\varphi \in C^1(U, V^\rho )$
and
![]() $\Phi \in \mathcal K_C$
. Take
$\Phi \in \mathcal K_C$
. Take
![]() $\delta> 0$
as in Lemma 5.1 and suppose that we have
$\delta> 0$
as in Lemma 5.1 and suppose that we have
 $$ \begin{align*} \|\varphi(u)\|_{L^2(G)} &< \Phi(u),\\ \sup_{w\in T^1_uU} \|( d\varphi )_u(w)\| &< C \Phi(u) \end{align*} $$
$$ \begin{align*} \|\varphi(u)\|_{L^2(G)} &< \Phi(u),\\ \sup_{w\in T^1_uU} \|( d\varphi )_u(w)\| &< C \Phi(u) \end{align*} $$
for all
![]() $u \in U$
. If
$u \in U$
. If
![]() $v^{(n)}$
is a past defined on
$v^{(n)}$
is a past defined on
![]() $B_\delta (u_0)$
satisfying
$B_\delta (u_0)$
satisfying
 $$ \begin{align*} \| \varphi ( v^{(n)}(u) ) \|_{L^2(G)} \geq \tfrac 1 4 \Phi( v^{(n)}(u) ) \end{align*} $$
$$ \begin{align*} \| \varphi ( v^{(n)}(u) ) \|_{L^2(G)} \geq \tfrac 1 4 \Phi( v^{(n)}(u) ) \end{align*} $$
for all
![]() $u \in B_\delta (u_0)$
, and some given
$u \in B_\delta (u_0)$
, and some given
![]() $u_0 \in U$
, then we have
$u_0 \in U$
, then we have

for all
![]() $u \in B_\delta (u_0)$
.
$u \in B_\delta (u_0)$
.
Proof. Differentiating the fraction, we see that we need to bound the supremum of

for any
![]() $u \in U$
and
$u \in U$
and
![]() $w \in T^1_u B_\delta (u_0)$
. Note that we always have
$w \in T^1_u B_\delta (u_0)$
. Note that we always have
 $$ \begin{align*} ( d( \| \varphi \circ v^{(n)} \|_{L^2(G)} ) )_u(w) \leq \| ( d( \varphi \circ v^{(n)} ) )_u(w) \|_{L^2(G)} \end{align*} $$
$$ \begin{align*} ( d( \| \varphi \circ v^{(n)} \|_{L^2(G)} ) )_u(w) \leq \| ( d( \varphi \circ v^{(n)} ) )_u(w) \|_{L^2(G)} \end{align*} $$
and so (5.4) is at most

by the triangle inequality. Cancelling terms, we can reduce (5.5) to

which is at most

by the chain rule. As
![]() $f \kappa ^n$
is the slowest expansion rate of any vector in
$f \kappa ^n$
is the slowest expansion rate of any vector in
![]() $T^1U$
under
$T^1U$
under
![]() $d\sigma ^n$
, we can bound
$d\sigma ^n$
, we can bound
 $$ \begin{align*} {\sup_{w \in T^1_uU}} \| ( dv^{(n)} )_u(w) \|_{T^1N} \leq \frac 1 { f \kappa^n} \end{align*} $$
$$ \begin{align*} {\sup_{w \in T^1_uU}} \| ( dv^{(n)} )_u(w) \|_{T^1N} \leq \frac 1 { f \kappa^n} \end{align*} $$
for all
![]() $u \in U$
. By hypothesis, we also have
$u \in U$
. By hypothesis, we also have
 $$ \begin{align*} \sup_{w' \in T^1_{v^{(n)}(u)}U} \| ( d\varphi )_{v^{(n)}(u)}(w')\|_{L^2(G)} \leq C \Phi( v^{(n)}(u) ) \end{align*} $$
$$ \begin{align*} \sup_{w' \in T^1_{v^{(n)}(u)}U} \| ( d\varphi )_{v^{(n)}(u)}(w')\|_{L^2(G)} \leq C \Phi( v^{(n)}(u) ) \end{align*} $$
for all
![]() $u \in U$
, and so (5.6) can be bounded above by
$u \in U$
, and so (5.6) can be bounded above by

which is, in turn, at most
 $$ \begin{align*} \frac {8 C \Phi( v^{(n)}(u) )}{f\kappa^n \Phi( v^{(n)}(u) )} \end{align*} $$
$$ \begin{align*} \frac {8 C \Phi( v^{(n)}(u) )}{f\kappa^n \Phi( v^{(n)}(u) )} \end{align*} $$
by hypothesis. Cancelling
![]() $\Phi $
, we obtain the result desired.
$\Phi $
, we obtain the result desired.
We need a simple lemma before proceeding to the main argument of the section; the proof is a straightforward application of the polarization identity.
Proposition 5.3. Let
![]() $(V, \cdot )$
be an inner product space, and suppose that we have
$(V, \cdot )$
be an inner product space, and suppose that we have
for
![]() $v, w \in V$
and
$v, w \in V$
and
![]() $\epsilon < 1$
, where
$\epsilon < 1$
, where
![]() $\hat v, \hat w$
denote the unit vectors in the directions of v and w, respectively. If
$\hat v, \hat w$
denote the unit vectors in the directions of v and w, respectively. If
![]() $\|v\| \leq \|w\|$
, then
$\|v\| \leq \|w\|$
, then
 $$ \begin{align*} \| v + w \| \, \leq \bigg( 1 - \frac {\epsilon^2} 4 \bigg)\|v\| + \|w\|. \end{align*} $$
$$ \begin{align*} \| v + w \| \, \leq \bigg( 1 - \frac {\epsilon^2} 4 \bigg)\|v\| + \|w\|. \end{align*} $$
We might be tempted to argue that, if
![]() $\varphi \in C^1(U, V^\rho )$
is controlled by
$\varphi \in C^1(U, V^\rho )$
is controlled by
![]() $\Phi \in \mathcal K_C$
as in Lemma 5.1, then we can similarly bound
$\Phi \in \mathcal K_C$
as in Lemma 5.1, then we can similarly bound
![]() $\| (\mathcal L^n_{z,\rho } \varphi )(u) \|_{L^2(G)}$
by
$\| (\mathcal L^n_{z,\rho } \varphi )(u) \|_{L^2(G)}$
by
 $(\mathcal L^n_{\mathrm {Re}(z),0} \Phi )(u)$
pointwise; however, although this turns out to be true, it is not particularly helpful because
$(\mathcal L^n_{\mathrm {Re}(z),0} \Phi )(u)$
pointwise; however, although this turns out to be true, it is not particularly helpful because
 $\mathcal L^n_{P(\varsigma ),0} \Phi $
fails to contract as
$\mathcal L^n_{P(\varsigma ),0} \Phi $
fails to contract as
![]() $n \to \infty $
. Indeed, because
$n \to \infty $
. Indeed, because
![]() $\Phi $
is strictly positive by definition,
$\Phi $
is strictly positive by definition,
 $\mathcal L^n_{P(\varsigma ),0} \Phi $
will converge to
$\mathcal L^n_{P(\varsigma ),0} \Phi $
will converge to
![]() $\int _U \Phi \, d\nu ^u> 0$
.
$\int _U \Phi \, d\nu ^u> 0$
.
The solution is to artificially introduce contraction into the transfer operators, and Theorem 4.16 is precisely what ensures that we can do this while maintaining a pointwise bound. In the next lemma, we show that we can uniformly and explicitly bound
![]() $\| ( \mathcal L^n_{z,\rho } \varphi )(u) \|_{L^2(G)}$
away from
$\| ( \mathcal L^n_{z,\rho } \varphi )(u) \|_{L^2(G)}$
away from
 $( \mathcal L^n_{\mathrm {Re}(z),0} \Phi )(u)$
on a measurable portion of any sufficiently small set.
$( \mathcal L^n_{\mathrm {Re}(z),0} \Phi )(u)$
on a measurable portion of any sufficiently small set.
The following lemma establishes the key cancellation mechanism in our setting, and mirrors [Reference Sharp17, Lemma 6.6] and, together with Lemma 5.5, is analogous to [Reference Dolgopyat11, §8].
Lemma 5.4. Fix
![]() $C> 0$
,
$C> 0$
,
![]() $\varphi \in C^1(U, V^\rho )$
and
$\varphi \in C^1(U, V^\rho )$
and
![]() $\Phi \in \mathcal K_C$
with
$\Phi \in \mathcal K_C$
with
 $$ \begin{align*} \| \varphi(u) \|_{L^2(G)} &< \Phi(u),\\ \sup_{w \in T_u^1U} \| ( d\varphi )_u(w) \|_{L^2(G)} &< C \Phi(u) \end{align*} $$
$$ \begin{align*} \| \varphi(u) \|_{L^2(G)} &< \Phi(u),\\ \sup_{w \in T_u^1U} \| ( d\varphi )_u(w) \|_{L^2(G)} &< C \Phi(u) \end{align*} $$
for all
![]() $u \in U$
. Let
$u \in U$
. Let
![]() $U_{lni} \subset U$
be the open subset given by Theorem 4.16 and let
$U_{lni} \subset U$
be the open subset given by Theorem 4.16 and let
![]() $\delta> 0$
be the constant given by Lemma 5.1. There are constants
$\delta> 0$
be the constant given by Lemma 5.1. There are constants
![]() $n_0> 0$
,
$n_0> 0$
,
![]() $\epsilon> 0$
and
$\epsilon> 0$
and
![]() $s < 1$
so that, for any
$s < 1$
so that, for any
![]() $x \in U_{lni}$
with
$x \in U_{lni}$
with
![]() $B_\delta (x) \subset U_{lni}$
, we can find
$B_\delta (x) \subset U_{lni}$
, we can find
-
• a point
 $y \in U_{lni}$
with
$y \in U_{lni}$
with
 $B_{s\delta }(y) \subset B_\delta (x)$
; and
$B_{s\delta }(y) \subset B_\delta (x)$
; and -
• a pair of pasts
 $v_1^{(n_0)}, v_2^{(n_0)}$
defined on
$v_1^{(n_0)}, v_2^{(n_0)}$
defined on
 $B_\delta (x)$
;
$B_\delta (x)$
;
for which we can bound
 $$ \begin{align*} &\|e^{\alpha_z^{(n_0)}(v_1^{(n_0)}(u))}\rho( \operatorname{\mathrm{Hol}}^{(n_0)}( v_1^{(n_0)}(u) ) ) \varphi( v_1^{(n_0)}(u) )\\ &\quad+\, e^{\alpha_z^{(n_0)}(v_2^{(n_0)}(u))}\rho( \operatorname{\mathrm{Hol}}^{(n_0)} ( v_2^{(n_0)}(u) ) ) \varphi( v_2^{(n_0)}(u) ) \|_{L^2(G)} \end{align*} $$
$$ \begin{align*} &\|e^{\alpha_z^{(n_0)}(v_1^{(n_0)}(u))}\rho( \operatorname{\mathrm{Hol}}^{(n_0)}( v_1^{(n_0)}(u) ) ) \varphi( v_1^{(n_0)}(u) )\\ &\quad+\, e^{\alpha_z^{(n_0)}(v_2^{(n_0)}(u))}\rho( \operatorname{\mathrm{Hol}}^{(n_0)} ( v_2^{(n_0)}(u) ) ) \varphi( v_2^{(n_0)}(u) ) \|_{L^2(G)} \end{align*} $$
above by
 $$ \begin{align*} \bigg( 1 - \frac {( \epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2}{4096} \bigg) e^{\alpha_{\mathrm{Re}(z)}^{(n_0)}(v_1^{(n_0)}(u))} \Phi( v_1^{(n_0)}(u) ) + e^{\alpha_{\mathrm{Re}(z)}^{(n_0)}(v_2^{(n_0)}(u))} \Phi( v_2^{(n_0)}(u) ) \end{align*} $$
$$ \begin{align*} \bigg( 1 - \frac {( \epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2}{4096} \bigg) e^{\alpha_{\mathrm{Re}(z)}^{(n_0)}(v_1^{(n_0)}(u))} \Phi( v_1^{(n_0)}(u) ) + e^{\alpha_{\mathrm{Re}(z)}^{(n_0)}(v_2^{(n_0)}(u))} \Phi( v_2^{(n_0)}(u) ) \end{align*} $$
for all
![]() $u \in B_{s\delta }(y)$
and all
$u \in B_{s\delta }(y)$
and all
![]() $z \in \mathbb {C}$
with
$z \in \mathbb {C}$
with
![]() $|\mathrm {Re}(z) - P(\varsigma ) | < 1$
. The constant
$|\mathrm {Re}(z) - P(\varsigma ) | < 1$
. The constant
![]() $\epsilon $
can be chosen independently of
$\epsilon $
can be chosen independently of
![]() $\rho $
and C, whereas
$\rho $
and C, whereas
![]() $n_0$
depends only on
$n_0$
depends only on
![]() $ C/{\|\rho \|}$
. The constant s can be chosen uniformly in C and
$ C/{\|\rho \|}$
. The constant s can be chosen uniformly in C and
![]() $\rho $
.
$\rho $
.
Proof. We deal with a fixed
![]() $n> 0$
throughout the proof, and specify how large n needs to be as we proceed; it is important to note that we cannot deal with arbitrarily large n without foregoing the uniformity of the bounds we wish to obtain. We proceed in cases depending on which alternative of Lemma 5.1 holds. For any pasts
$n> 0$
throughout the proof, and specify how large n needs to be as we proceed; it is important to note that we cannot deal with arbitrarily large n without foregoing the uniformity of the bounds we wish to obtain. We proceed in cases depending on which alternative of Lemma 5.1 holds. For any pasts
 $v_1^{(n)}$
and
$v_1^{(n)}$
and
 $v_2^{(n)}$
, if we have
$v_2^{(n)}$
, if we have
 $$ \begin{align*} \|\varphi(v_{1}^{(n)}(u))\|_{L^2(G)} \leq \tfrac 3 4 \Phi( v_{1}^{(n)}(u) ) \end{align*} $$
$$ \begin{align*} \|\varphi(v_{1}^{(n)}(u))\|_{L^2(G)} \leq \tfrac 3 4 \Phi( v_{1}^{(n)}(u) ) \end{align*} $$
for all
![]() $u \in B_\delta (x)$
, then because
$u \in B_\delta (x)$
, then because
![]() $\rho $
is unitary we can clearly bound
$\rho $
is unitary we can clearly bound

above by
 $$ \begin{align*} \tfrac 3 4 (e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u))} \Phi( v_1^{(n)}(u) ) + e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u))} \Phi( v_2^{(n)}(u) ) ) \end{align*} $$
$$ \begin{align*} \tfrac 3 4 (e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u))} \Phi( v_1^{(n)}(u) ) + e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u))} \Phi( v_2^{(n)}(u) ) ) \end{align*} $$
for all
![]() $u \in B_\delta (x)$
. In this case, we are done by simply setting
$u \in B_\delta (x)$
. In this case, we are done by simply setting
![]() $y := x$
. Similarly, if we had
$y := x$
. Similarly, if we had
 $$ \begin{align*} \|\varphi(v_{2}^{(n)}(u))\|_{L^2(G)} \leq \tfrac 3 4 \Phi( v_{2}^{(n)}(u) ) \end{align*} $$
$$ \begin{align*} \|\varphi(v_{2}^{(n)}(u))\|_{L^2(G)} \leq \tfrac 3 4 \Phi( v_{2}^{(n)}(u) ) \end{align*} $$
for all
![]() $u \in B_\delta (x)$
, then we are again done by setting
$u \in B_\delta (x)$
, then we are again done by setting
![]() $y := x$
, up to interchanging our choice of
$y := x$
, up to interchanging our choice of
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. So we may as well assume that the second alternative of Lemma 5.1 holds for both
$v_2$
. So we may as well assume that the second alternative of Lemma 5.1 holds for both
 $v_1^{(n)}$
and
$v_1^{(n)}$
and
 $v_2^{(n)}$
, and that we therefore have
$v_2^{(n)}$
, and that we therefore have
 $$ \begin{align} \|\varphi(v_{\ell}^{(n)}(u))\|_{L^2(G)} \geq \tfrac 1 4 \Phi( v_{\ell}^{(n)}(u) ) \end{align} $$
$$ \begin{align} \|\varphi(v_{\ell}^{(n)}(u))\|_{L^2(G)} \geq \tfrac 1 4 \Phi( v_{\ell}^{(n)}(u) ) \end{align} $$
for all
![]() $u \in B_\delta (x)$
. We temporarily abbreviate
$u \in B_\delta (x)$
. We temporarily abbreviate

and

for the sake of clarity. Note that
![]() $\hat \varphi _\ell $
and
$\hat \varphi _\ell $
and
![]() $\hat \psi _\ell $
are well-defined on
$\hat \psi _\ell $
are well-defined on
![]() $B_\delta (x)$
as an immediate consequence of (5.7). Now, by reversing the triangle inequality,
$B_\delta (x)$
as an immediate consequence of (5.7). Now, by reversing the triangle inequality,

is at least

for any
![]() $y \in B_\delta (x)$
. As group elements act by isometries with respect to the
$y \in B_\delta (x)$
. As group elements act by isometries with respect to the
![]() $L^2(G)$
norm, (5.9) is equal to
$L^2(G)$
norm, (5.9) is equal to

which we can bound below by

using the reverse triangle inequality once again. We can rewrite (5.10) as

by replacing
![]() $\hat \psi _1(y)$
with
$\hat \psi _1(y)$
with
 $g_1^{-1}(y)g_1(y)\hat \psi _1(y)$
in the first term of the first line, and multiplying both terms on the first line by
$g_1^{-1}(y)g_1(y)\hat \psi _1(y)$
in the first term of the first line, and multiplying both terms on the first line by
 $g_2(x)g_2^{-1}(y)$
. Hence, (5.8) is bounded below by (5.11), and we see that
$g_2(x)g_2^{-1}(y)$
. Hence, (5.8) is bounded below by (5.11), and we see that

is at least

after rearranging. By Theorem 4.16, there is an
![]() $N> 0$
,
$N> 0$
,
![]() $\epsilon> 0$
, a choice of pasts
$\epsilon> 0$
, a choice of pasts
 $v_1^{(n)}$
and
$v_1^{(n)}$
and
 $v_2^{(n)}$
, and a y with
$v_2^{(n)}$
, and a y with
![]() $d(x,y) = \delta /2$
for which we have
$d(x,y) = \delta /2$
for which we have
 $$ \begin{align} &\| \rho( g_{1}(x)g_1^{-1}(y)g_1(y) ) \hat\psi_{1}( y ) - \rho( g_2(x)g_2^{-1}(y)g_1(y) )\hat\psi_{1}( y )\|_{L^2(G)}\nonumber\\ &\quad\geq \epsilon (1+|\mathrm{Im}(z)|) \|\rho\| \frac \delta 2 \end{align} $$
$$ \begin{align} &\| \rho( g_{1}(x)g_1^{-1}(y)g_1(y) ) \hat\psi_{1}( y ) - \rho( g_2(x)g_2^{-1}(y)g_1(y) )\hat\psi_{1}( y )\|_{L^2(G)}\nonumber\\ &\quad\geq \epsilon (1+|\mathrm{Im}(z)|) \|\rho\| \frac \delta 2 \end{align} $$
for all
![]() $n \geq N$
; note that we have applied the theorem to
$n \geq N$
; note that we have applied the theorem to

which is certainly a smooth function in
![]() $C^1(U, V^\rho )$
. On the other hand, by Lemma 5.2,
$C^1(U, V^\rho )$
. On the other hand, by Lemma 5.2,
![]() $\hat \varphi _\ell (u)$
is at worst
$\hat \varphi _\ell (u)$
is at worst
![]() ${8C}/{f\kappa ^n}$
-Lipschitz in u on
${8C}/{f\kappa ^n}$
-Lipschitz in u on
![]() $B_\delta (x)$
, and we can estimate
$B_\delta (x)$
, and we can estimate

for all
![]() $u \in U$
,
$u \in U$
,
![]() $w \in T^1_uB_\delta (x)$
and
$w \in T^1_uB_\delta (x)$
and
 $w' \in T^1_{v_\ell (u)}B_\delta (x)$
. Hence, we can bound
$w' \in T^1_{v_\ell (u)}B_\delta (x)$
. Hence, we can bound
 $$ \begin{align*} \| \hat \psi_\ell(x) - \hat \psi_\ell(y) \| \leq \bigg(\frac {8C}{f\kappa^n} + |\mathrm{Im}(z)| \frac{\|\tau\|_{C^1}}{f(\kappa - 1)}\bigg)\,d(x,y) \end{align*} $$
$$ \begin{align*} \| \hat \psi_\ell(x) - \hat \psi_\ell(y) \| \leq \bigg(\frac {8C}{f\kappa^n} + |\mathrm{Im}(z)| \frac{\|\tau\|_{C^1}}{f(\kappa - 1)}\bigg)\,d(x,y) \end{align*} $$
because we chose
![]() $y \in B_\delta (x)$
. Suppose that n and
$y \in B_\delta (x)$
. Suppose that n and
![]() $\|\rho \|$
are large enough so that we have
$\|\rho \|$
are large enough so that we have
 $$ \begin{align*} \bigg( \frac {8 C}{f \kappa^n} + |\mathrm{Im}(z)| \frac{\|\tau\|_{C^1}}{f(\kappa -1)} \bigg) < \frac {\epsilon} 8 (1+|\mathrm{Im}(z)|) \|\rho\| \end{align*} $$
$$ \begin{align*} \bigg( \frac {8 C}{f \kappa^n} + |\mathrm{Im}(z)| \frac{\|\tau\|_{C^1}}{f(\kappa -1)} \bigg) < \frac {\epsilon} 8 (1+|\mathrm{Im}(z)|) \|\rho\| \end{align*} $$
for some constant
![]() $K> 0$
. Note that we can make this choice of n so that it depends only on
$K> 0$
. Note that we can make this choice of n so that it depends only on
![]() $ C /{\|\rho \|}$
and not
$ C /{\|\rho \|}$
and not
![]() $\|\rho \|$
directly; moreover, the requirement that
$\|\rho \|$
directly; moreover, the requirement that
![]() $\|\rho \|$
be sufficiently large can be made absolute, and in particular is independent of z. This ensures
$\|\rho \|$
be sufficiently large can be made absolute, and in particular is independent of z. This ensures
 $$ \begin{align} \| \hat \psi_\ell(x) - \hat \psi_\ell(y)\|_{L^2(G)} \leq \frac \epsilon 8 ( 1 + |\mathrm{Im}(z)| )\| \rho \| \delta \end{align} $$
$$ \begin{align} \| \hat \psi_\ell(x) - \hat \psi_\ell(y)\|_{L^2(G)} \leq \frac \epsilon 8 ( 1 + |\mathrm{Im}(z)| )\| \rho \| \delta \end{align} $$
because
![]() $d(x,y) \leq \delta $
. Note that our choice of n here depends only on
$d(x,y) \leq \delta $
. Note that our choice of n here depends only on
![]() $ C/ {\|\rho \|}$
. Plugging (5.13) and (5.14) into (5.12), we conclude that
$ C/ {\|\rho \|}$
. Plugging (5.13) and (5.14) into (5.12), we conclude that
 $$ \begin{align*} &\|\rho(g_1(x))\hat \psi_1(x) - \rho( g_2(x) )\hat \psi_2(x) \|_{L^2(G)} + \|\rho(g_1(y)) \hat\psi_1(y) - \rho( g_2(y) )\hat \psi_2(y)\|_{L^2(G)}\\ &\quad\geq \frac \epsilon 4 \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align*} $$
$$ \begin{align*} &\|\rho(g_1(x))\hat \psi_1(x) - \rho( g_2(x) )\hat \psi_2(x) \|_{L^2(G)} + \|\rho(g_1(y)) \hat\psi_1(y) - \rho( g_2(y) )\hat \psi_2(y)\|_{L^2(G)}\\ &\quad\geq \frac \epsilon 4 \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align*} $$
and so
 $$ \begin{align} \|\rho(g_1(x))\hat \psi_1(x) - \rho( g_2(x) )\hat \psi_2(x) \|_{L^2(G)}> \frac \epsilon 8 \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align} $$
$$ \begin{align} \|\rho(g_1(x))\hat \psi_1(x) - \rho( g_2(x) )\hat \psi_2(x) \|_{L^2(G)}> \frac \epsilon 8 \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align} $$
or
 $$ \begin{align} \|\rho(g_1(y))\hat \psi_1(y) - \rho( g_2(y) )\hat \psi_2(y) \|_{L^2(G)}> \frac \epsilon 8 \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align} $$
$$ \begin{align} \|\rho(g_1(y))\hat \psi_1(y) - \rho( g_2(y) )\hat \psi_2(y) \|_{L^2(G)}> \frac \epsilon 8 \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align} $$
must hold. Without loss of generality, suppose (5.16) holds. Using the Lipschitz estimate on
![]() $\hat \varphi _\ell $
, we can bound
$\hat \varphi _\ell $
, we can bound
 $$ \begin{align*} \sup_{w \in T^1_uB_\delta(x)} \| ( d( \rho ( g_\ell ) \hat \psi_\ell ) )_u(w) \|_{L^2(G)} \end{align*} $$
$$ \begin{align*} \sup_{w \in T^1_uB_\delta(x)} \| ( d( \rho ( g_\ell ) \hat \psi_\ell ) )_u(w) \|_{L^2(G)} \end{align*} $$
by
 $$ \begin{align} \sup_{w \in T^1_uB_\delta(x)} \| (( (d\rho)_{g_\ell(u)} \circ ( dg_\ell )_u )(w)) \hat \psi_\ell(u) + \rho( g_\ell(u) ) ( d \hat \psi_\ell )_u(w)\|_{L^2(G)} \end{align} $$
$$ \begin{align} \sup_{w \in T^1_uB_\delta(x)} \| (( (d\rho)_{g_\ell(u)} \circ ( dg_\ell )_u )(w)) \hat \psi_\ell(u) + \rho( g_\ell(u) ) ( d \hat \psi_\ell )_u(w)\|_{L^2(G)} \end{align} $$
for all
![]() $u \in B_\delta (x)$
. A straightforward calculation shows that
$u \in B_\delta (x)$
. A straightforward calculation shows that

and we have
 $$ \begin{align*} \sup_{w' \in T^1_{g_\ell(u)}G} \| ( d\rho )_{g_\ell(u)}(w') \|_{L^2(G)} \leq \|\rho\| \end{align*} $$
$$ \begin{align*} \sup_{w' \in T^1_{g_\ell(u)}G} \| ( d\rho )_{g_\ell(u)}(w') \|_{L^2(G)} \leq \|\rho\| \end{align*} $$
by Definition 2.9; note that because
![]() $\rho $
is a homomorphism, the operator norm of
$\rho $
is a homomorphism, the operator norm of
![]() $d\rho $
at
$d\rho $
at
![]() $g_\ell (u)$
is equivalent to the norm at the identity. Hence, (5.17) is at most
$g_\ell (u)$
is equivalent to the norm at the identity. Hence, (5.17) is at most

by our choice of
![]() $\delta $
, because
$\delta $
, because
![]() $\rho $
acts by
$\rho $
acts by
![]() $L^2(G)$
-isometries. We can make a uniform choice of
$L^2(G)$
-isometries. We can make a uniform choice of
![]() $s < 1$
so that
$s < 1$
so that

and we then have
 $$ \begin{align} \| \rho( g_1(y) ) \hat \psi_1(y) - \rho ( g_1(u) ) \hat \psi_1(u) \|_{L^2(G)} < \frac \epsilon {32} \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align} $$
$$ \begin{align} \| \rho( g_1(y) ) \hat \psi_1(y) - \rho ( g_1(u) ) \hat \psi_1(u) \|_{L^2(G)} < \frac \epsilon {32} \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align} $$
and
 $$ \begin{align} \| \rho( g_2(y) ) \hat \psi_2(y) - \rho ( g_2(u) ) \hat \psi_2(u) \|_{L^2(G)} < \frac \epsilon {32} \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align} $$
$$ \begin{align} \| \rho( g_2(y) ) \hat \psi_2(y) - \rho ( g_2(u) ) \hat \psi_2(u) \|_{L^2(G)} < \frac \epsilon {32} \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align} $$
for all
![]() $u \in B_{s\delta }(y)$
. Combining (5.19) and (5.20) with (5.15), we now have
$u \in B_{s\delta }(y)$
. Combining (5.19) and (5.20) with (5.15), we now have
 $$ \begin{align*} \| \rho( g_1(u) )\hat \psi_1(u) - \rho ( g_2(u) ) \hat \psi_2(u) \|_{L^2(G)}> \frac \epsilon {16} \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align*} $$
$$ \begin{align*} \| \rho( g_1(u) )\hat \psi_1(u) - \rho ( g_2(u) ) \hat \psi_2(u) \|_{L^2(G)}> \frac \epsilon {16} \delta (1+|\mathrm{Im}(z)|) \|\rho\| \end{align*} $$
for all
![]() $u \in B_{s\delta }(y)$
. Now, fix
$u \in B_{s\delta }(y)$
. Now, fix
![]() $u \in B_{s\delta }(y)$
. By Proposition 5.3, we can then bound
$u \in B_{s\delta }(y)$
. By Proposition 5.3, we can then bound

above by
 $$ \begin{align} \bigg( 1 - \frac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| \|)^2}{1024} \bigg) e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u))} \Phi( v_1^{(n)}(u) ) + e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u))} \Phi( v_2^{(n)}(u) ) \end{align} $$
$$ \begin{align} \bigg( 1 - \frac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| \|)^2}{1024} \bigg) e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u))} \Phi( v_1^{(n)}(u) ) + e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u))} \Phi( v_2^{(n)}(u) ) \end{align} $$
assuming without loss of generality that
 $$ \begin{align} \|e^{\alpha_{\mathrm{Re}(z)}^{(n)}( v_1^{(n)}(u) )} \varphi( v_1^{(n)}(u) )\|_{L^2(G)} \leq \|e^{\alpha_{\mathrm{Re}(z)}^{(n)}( v_2^{(n)}(u) )} \varphi( v_2^{(n)}(u) )\|_{L^2(G)} \end{align} $$
$$ \begin{align} \|e^{\alpha_{\mathrm{Re}(z)}^{(n)}( v_1^{(n)}(u) )} \varphi( v_1^{(n)}(u) )\|_{L^2(G)} \leq \|e^{\alpha_{\mathrm{Re}(z)}^{(n)}( v_2^{(n)}(u) )} \varphi( v_2^{(n)}(u) )\|_{L^2(G)} \end{align} $$
held for this particular u; this is true up to interchanging
 $v_1^{(n)}$
and
$v_1^{(n)}$
and
 $v_2^{(n)}$
. It simply remains to ensure that a similar inequality extends to
$v_2^{(n)}$
. It simply remains to ensure that a similar inequality extends to
![]() $B_{s\delta }(y)$
for this particular choice of
$B_{s\delta }(y)$
for this particular choice of
 $v_1^{(n)}$
and
$v_1^{(n)}$
and
 $v_2^{(n)}$
: this is not immediate because (5.22) could certainly fail to hold on the entire ball
$v_2^{(n)}$
: this is not immediate because (5.22) could certainly fail to hold on the entire ball
![]() $B_{s\delta }(y)$
.
$B_{s\delta }(y)$
.
This requires some extra work. Note that we have
 $$ \begin{align*} &\sup_{w \in T^1_uU} \bigg\| \bigg(d \bigg(e^{\alpha_{\mathrm{Re}(z)}^{(n)}} \Phi \bigg) \bigg)_u(w) \bigg\|_{L^2(G)} \\ &\quad\leq \sup_{w \in T^1_uU} |(de^{\alpha_{\mathrm{Re}(z)}^{(n)}})_u(w) | \| \Phi(u) \|_{L^2(G)} + e^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)}\| ( d \Phi )_u(w) \|_{L^2(G)} \\ &\quad\leq \|\alpha_{\mathrm{Re}(z)}^{(n)} \|_{C^1} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)} \| \Phi(u) \|_{L^2(G)} + Ce^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)}\Phi(u)\\ &\quad\leq \bigg(\sum_{i=1}^{n} bK^i \|\alpha_{\mathrm{Re}(z)}\|_{C^1}\bigg)e^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)} \| \Phi(u) \|_{L^2(G)} + Ce^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)}\Phi(u)\\ &\quad\leq \bigg( b \|\alpha_{\mathrm{Re}(z)}\|_{C^1} \frac{K^{n+1} - K}{K - 1} + C \bigg) e^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)} \|\Phi(u)\|_{L^2(G)} \end{align*} $$
$$ \begin{align*} &\sup_{w \in T^1_uU} \bigg\| \bigg(d \bigg(e^{\alpha_{\mathrm{Re}(z)}^{(n)}} \Phi \bigg) \bigg)_u(w) \bigg\|_{L^2(G)} \\ &\quad\leq \sup_{w \in T^1_uU} |(de^{\alpha_{\mathrm{Re}(z)}^{(n)}})_u(w) | \| \Phi(u) \|_{L^2(G)} + e^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)}\| ( d \Phi )_u(w) \|_{L^2(G)} \\ &\quad\leq \|\alpha_{\mathrm{Re}(z)}^{(n)} \|_{C^1} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)} \| \Phi(u) \|_{L^2(G)} + Ce^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)}\Phi(u)\\ &\quad\leq \bigg(\sum_{i=1}^{n} bK^i \|\alpha_{\mathrm{Re}(z)}\|_{C^1}\bigg)e^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)} \| \Phi(u) \|_{L^2(G)} + Ce^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)}\Phi(u)\\ &\quad\leq \bigg( b \|\alpha_{\mathrm{Re}(z)}\|_{C^1} \frac{K^{n+1} - K}{K - 1} + C \bigg) e^{\alpha_{\mathrm{Re}(z)}^{(n)}(u)} \|\Phi(u)\|_{L^2(G)} \end{align*} $$
for all
![]() $u \in U$
. By making s smaller if necessary, we can ensure that, in addition to (5.18), we also have
$u \in U$
. By making s smaller if necessary, we can ensure that, in addition to (5.18), we also have
 $$ \begin{align*} s\delta( b \|\alpha_{\mathrm{Re}(z)}\|_{C^1} \frac{K^{n+1} - K}{K - 1} + C ) < \delta C = A, \end{align*} $$
$$ \begin{align*} s\delta( b \|\alpha_{\mathrm{Re}(z)}\|_{C^1} \frac{K^{n+1} - K}{K - 1} + C ) < \delta C = A, \end{align*} $$
where A is the uniform constant guaranteed by Lemma 5.1. Note that this can be accomplished by a uniform choice of s, because n is fixed and z is required to satisfy
![]() $| \mathrm {Re}(z) - P(\varsigma ) | < 1$
. As a consequence, we see by Lemma 5.1 that
$| \mathrm {Re}(z) - P(\varsigma ) | < 1$
. As a consequence, we see by Lemma 5.1 that
 $$ \begin{align} \tfrac 1 2 e^{\alpha^{(n)}_{\mathrm{Re}(z)}( v_\ell^{(n)}(u') )} \Phi ( v_\ell^{(n)}(u') ) \leq e^{\alpha^{(n)}_{\mathrm{Re}(z)}( v_\ell^{(n)}(u) )} \Phi ( v_\ell^{(n)}(u) ) \leq 2e^{\alpha^{(n)}_{\mathrm{Re}(z)}( v_\ell^{(n)}(u') )} \Phi ( v_\ell^{(n)}(u') ) \end{align} $$
$$ \begin{align} \tfrac 1 2 e^{\alpha^{(n)}_{\mathrm{Re}(z)}( v_\ell^{(n)}(u') )} \Phi ( v_\ell^{(n)}(u') ) \leq e^{\alpha^{(n)}_{\mathrm{Re}(z)}( v_\ell^{(n)}(u) )} \Phi ( v_\ell^{(n)}(u) ) \leq 2e^{\alpha^{(n)}_{\mathrm{Re}(z)}( v_\ell^{(n)}(u') )} \Phi ( v_\ell^{(n)}(u') ) \end{align} $$
for all
![]() $u, u' \in B_{s\delta }(y)$
. Now, suppose that
$u, u' \in B_{s\delta }(y)$
. Now, suppose that

were bounded above by
 $$ \begin{align} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u'))} \Phi( v_1^{(n)}(u') ) + \bigg( 1 - \frac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2}{1024} \bigg) e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u'))} \Phi( v_2^{(n)}(u') ) \end{align} $$
$$ \begin{align} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u'))} \Phi( v_1^{(n)}(u') ) + \bigg( 1 - \frac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2}{1024} \bigg) e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u'))} \Phi( v_2^{(n)}(u') ) \end{align} $$
for some
![]() $u' \in B_{s\delta }(y)$
; this is in contrast to the bound by (5.21) that we have at
$u' \in B_{s\delta }(y)$
; this is in contrast to the bound by (5.21) that we have at
![]() $u \in B_{s\delta }(y)$
. If we had
$u \in B_{s\delta }(y)$
. If we had
 $$ \begin{align*} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u'))} \Phi( v_2^{(n)}(u') ) \leq e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u'))} \Phi( v_1^{(n)}(u') ), \end{align*} $$
$$ \begin{align*} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u'))} \Phi( v_2^{(n)}(u') ) \leq e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u'))} \Phi( v_1^{(n)}(u') ), \end{align*} $$
then (5.24) is, in turn, bounded above by
 $$ \begin{align*} \bigg( 1 - \frac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2}{1024} \bigg)e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u'))} \Phi( v_1^{(n)}(u') ) + e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u'))} \Phi( v_2^{(n)}(u') ), \end{align*} $$
$$ \begin{align*} \bigg( 1 - \frac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2}{1024} \bigg)e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u'))} \Phi( v_1^{(n)}(u') ) + e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u'))} \Phi( v_2^{(n)}(u') ), \end{align*} $$
which is consistent with (5.21). If, on the other hand, we had
 $$ \begin{align*} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u'))} \Phi( v_1^{(n)}(u') ) \leq e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u'))} \Phi( v_2^{(n)}(u') ), \end{align*} $$
$$ \begin{align*} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u'))} \Phi( v_1^{(n)}(u') ) \leq e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u'))} \Phi( v_2^{(n)}(u') ), \end{align*} $$
then we can invoke (5.23) twice to see that
 $$ \begin{align*} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u))} \Phi( v_1^{(n)}(u) ) &\leq 2 e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u'))} \Phi( v_1^{(n)}(u') )\\ &\leq 2e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u'))} \Phi( v_2^{(n)}(u') )\\ &\leq 4e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u))} \Phi( v_2^{(n)}(u) ) \end{align*} $$
$$ \begin{align*} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u))} \Phi( v_1^{(n)}(u) ) &\leq 2 e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u'))} \Phi( v_1^{(n)}(u') )\\ &\leq 2e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u'))} \Phi( v_2^{(n)}(u') )\\ &\leq 4e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u))} \Phi( v_2^{(n)}(u) ) \end{align*} $$
for any other
![]() $u \in B_{s\delta }(y)$
. Hence, (5.21) is at most
$u \in B_{s\delta }(y)$
. Hence, (5.21) is at most
 $$ \begin{align*} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u))} \Phi( v_1^{(n)}(u) ) + \bigg( 1 - \frac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2}{4096} \bigg) e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u))} \Phi( v_2^{(n)}(u) ) \end{align*} $$
$$ \begin{align*} e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_1^{(n)}(u))} \Phi( v_1^{(n)}(u) ) + \bigg( 1 - \frac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2}{4096} \bigg) e^{\alpha_{\mathrm{Re}(z)}^{(n)}(v_2^{(n)}(u))} \Phi( v_2^{(n)}(u) ) \end{align*} $$
and so we can make a consistent choice of
 $v_1^{(n)}, v_2^{(n)}$
on the entire ball
$v_1^{(n)}, v_2^{(n)}$
on the entire ball
![]() $B_{s\delta }(y)$
. Note that if (5.15) held instead, everything that followed would have been identical, with
$B_{s\delta }(y)$
. Note that if (5.15) held instead, everything that followed would have been identical, with
![]() $B_{s\delta }(x)$
instead of
$B_{s\delta }(x)$
instead of
![]() $B_{s\delta }(y)$
.
$B_{s\delta }(y)$
.
The point of Lemma 5.4 is that, in any ball
![]() $B_\delta (x)$
of radius
$B_\delta (x)$
of radius
![]() $\delta $
, we can always find a uniformly smaller ball
$\delta $
, we can always find a uniformly smaller ball
![]() $B_{s\delta }(y) \subset B_\delta (x)$
on which
$B_{s\delta }(y) \subset B_\delta (x)$
on which
![]() $\mathcal L^n_{z,\rho } \varphi $
is strictly and uniformly bounded away from
$\mathcal L^n_{z,\rho } \varphi $
is strictly and uniformly bounded away from
 $\mathcal L^n_{\mathrm {Re}(z),0}( \Phi )$
. This means that we can ‘bump’
$\mathcal L^n_{\mathrm {Re}(z),0}( \Phi )$
. This means that we can ‘bump’
![]() $\Phi $
down on any such ball
$\Phi $
down on any such ball
![]() $B_{ \delta /4}(y)$
without affecting our inequality. Moreover, using the diametric regularity of the measure
$B_{ \delta /4}(y)$
without affecting our inequality. Moreover, using the diametric regularity of the measure
![]() $\nu ^u$
, we can ensure that we are able to do this on a set of uniformly large measure.
$\nu ^u$
, we can ensure that we are able to do this on a set of uniformly large measure.
Lemma 5.5. Fix
![]() $C> 0$
,
$C> 0$
,
![]() $\varphi \in C^1(U, V^\rho )$
and
$\varphi \in C^1(U, V^\rho )$
and
![]() $\Phi \in \mathcal K_{C}$
. Suppose we have
$\Phi \in \mathcal K_{C}$
. Suppose we have
 $$ \begin{align*} \| \varphi(u) \|_{L^2(G)} &< \Phi(u),\\ \sup_{w \in T_u^1U} \| ( d\varphi )_u(w) \|_{L^2(G)} &< C \Phi(u) \end{align*} $$
$$ \begin{align*} \| \varphi(u) \|_{L^2(G)} &< \Phi(u),\\ \sup_{w \in T_u^1U} \| ( d\varphi )_u(w) \|_{L^2(G)} &< C \Phi(u) \end{align*} $$
for all
![]() $u \in U$
, and let
$u \in U$
, and let
![]() $\delta> 0$
be the constant guaranteed by Lemma 5.1 and
$\delta> 0$
be the constant guaranteed by Lemma 5.1 and
![]() $n_0> 0$
,
$n_0> 0$
,
![]() $\epsilon> 0$
and
$\epsilon> 0$
and
![]() $s < 1$
be the constants guaranteed by Lemma 5.4. For a given
$s < 1$
be the constants guaranteed by Lemma 5.4. For a given
![]() $\rho $
and
$\rho $
and
![]() $z \in \mathbb {C}$
with
$z \in \mathbb {C}$
with
![]() $|\mathrm {Re}(z) - P(\varsigma )| < 1$
, we can find a function
$|\mathrm {Re}(z) - P(\varsigma )| < 1$
, we can find a function
![]() $\beta \in C^1(U, \mathbb {R})$
for which we have
$\beta \in C^1(U, \mathbb {R})$
for which we have
 $$ \begin{align*} \|(\mathcal L^{n_0}_{z,\rho} \varphi )(u)\|_{L^2(G)} \leq (\mathcal L^{n_0}_{\mathrm{Re}(z),0} (\beta\Phi)) (u) \end{align*} $$
$$ \begin{align*} \|(\mathcal L^{n_0}_{z,\rho} \varphi )(u)\|_{L^2(G)} \leq (\mathcal L^{n_0}_{\mathrm{Re}(z),0} (\beta\Phi)) (u) \end{align*} $$
for all
![]() $u \in U$
, as well as
$u \in U$
, as well as
 $$ \begin{align*} \| \mathcal L^{n_0}_{P(\varsigma),0} ( \beta \Phi ) \|_{L^2(\nu^u)} \leq \bigg( 1 - r \frac{(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2}{4096} \nu^u( U_{lni} ) \bigg) \| \Phi \|_{L^2(\nu^u)} \end{align*} $$
$$ \begin{align*} \| \mathcal L^{n_0}_{P(\varsigma),0} ( \beta \Phi ) \|_{L^2(\nu^u)} \leq \bigg( 1 - r \frac{(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2}{4096} \nu^u( U_{lni} ) \bigg) \| \Phi \|_{L^2(\nu^u)} \end{align*} $$
for some uniform constant
![]() $r < 1$
. The constant r depends on
$r < 1$
. The constant r depends on
![]() $n_0$
and C, but not on
$n_0$
and C, but not on
![]() $\rho $
, z,
$\rho $
, z,
![]() $\varphi $
or
$\varphi $
or
![]() $\Phi $
; the function
$\Phi $
; the function
![]() $\beta $
may depend on all of these.
$\beta $
may depend on all of these.
Proof. By the Vitali covering lemma, we can find a finite collection of points
![]() $x_1, \ldots , x_k \in U_{lni}$
so that the balls
$x_1, \ldots , x_k \in U_{lni}$
so that the balls
![]() $B_\delta (x_1), \ldots , B_\delta (x_k) \subset U_{lni}$
of radius
$B_\delta (x_1), \ldots , B_\delta (x_k) \subset U_{lni}$
of radius
![]() $\delta $
are pairwise disjoint, whereas the balls
$\delta $
are pairwise disjoint, whereas the balls
![]() $B_{3\delta }(x_1), \ldots , B_{3\delta }(x_k)$
of radius
$B_{3\delta }(x_1), \ldots , B_{3\delta }(x_k)$
of radius
![]() $3\delta $
cover
$3\delta $
cover
![]() $U_{lni}$
. By Lemma 5.4, for each i we can find a ball
$U_{lni}$
. By Lemma 5.4, for each i we can find a ball
![]() $B_{s\delta }(y_i) \subset B_{\delta } (x_i)$
and pasts
$B_{s\delta }(y_i) \subset B_{\delta } (x_i)$
and pasts
 $v_{1,i}^{(n_0)}, v_{2,i}^{(n_0)}$
so that
$v_{1,i}^{(n_0)}, v_{2,i}^{(n_0)}$
so that
 $$ \begin{align*} &\|e^{\alpha_z^{(n_0)}(v_{1,i}^{(n_0)}(u))}\rho( \operatorname{\mathrm{Hol}}^{(n_0)}( v_{1,i}^{(n_0)}(u) ) ) \varphi( v_{1,i}^{(n_0)}(u) )\\ &\quad+\, e^{\alpha_z^{(n_0)}(v_{2,i}^{(n_0)}(u))} \rho( \operatorname{\mathrm{Hol}}^{(n_0)} ( v_{2,i}^{(n_0)}(u) ) ) \varphi( v_{2,i}^{(n_0)}(u) ) \|_{L^2(G)} \end{align*} $$
$$ \begin{align*} &\|e^{\alpha_z^{(n_0)}(v_{1,i}^{(n_0)}(u))}\rho( \operatorname{\mathrm{Hol}}^{(n_0)}( v_{1,i}^{(n_0)}(u) ) ) \varphi( v_{1,i}^{(n_0)}(u) )\\ &\quad+\, e^{\alpha_z^{(n_0)}(v_{2,i}^{(n_0)}(u))} \rho( \operatorname{\mathrm{Hol}}^{(n_0)} ( v_{2,i}^{(n_0)}(u) ) ) \varphi( v_{2,i}^{(n_0)}(u) ) \|_{L^2(G)} \end{align*} $$
is bounded above by
 $$ \begin{align*} \bigg( 1 - \frac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2} {4096} \bigg)e^{\alpha_{\mathrm{Re}(z)}^{(n_0)}(v_{1,i}^{(n_0)}(u))} \Phi( v_{1,i}^{(n_0)}(u) ) + e^{\alpha_{\mathrm{Re}(z)}^{(n_0)}(v_{2,i}^{(n_0)}(u))} \Phi( v_{2,i}^{(n_0)}(u) ) \end{align*} $$
$$ \begin{align*} \bigg( 1 - \frac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2} {4096} \bigg)e^{\alpha_{\mathrm{Re}(z)}^{(n_0)}(v_{1,i}^{(n_0)}(u))} \Phi( v_{1,i}^{(n_0)}(u) ) + e^{\alpha_{\mathrm{Re}(z)}^{(n_0)}(v_{2,i}^{(n_0)}(u))} \Phi( v_{2,i}^{(n_0)}(u) ) \end{align*} $$
for all
![]() $u \in B_{s\delta }(y_i)$
. For each i, define a
$u \in B_{s\delta }(y_i)$
. For each i, define a
![]() $C^1$
radially decreasing bump function
$C^1$
radially decreasing bump function
![]() $\eta _i$
centred at
$\eta _i$
centred at
 $v_{1,i}^{(n_0)}(y_i)$
by
$v_{1,i}^{(n_0)}(y_i)$
by
 $$ \begin{align*} &\eta_i(v_1^{(n_0)}(u))\\ &\quad= \begin{cases} \dfrac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2} {4096} &\textrm{ if }\ d(u, y_i) \leq \dfrac {s\delta} 2,\\\\[-6pt] \dfrac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\|)^2}{4096}&\\\\[-6pt] \qquad\cdot\exp\bigg(1 + \dfrac{1}{( (1/ {s\delta})\, d(u,y_i) - ( 1/ 2) )^2 - 1}\bigg) &\textrm{ if }\ \dfrac {s\delta} 2 < d(u,y_i) < s\delta,\\ 0 &\textrm{ if }\ s\delta \leq d(u,y_i), \end{cases} \end{align*} $$
$$ \begin{align*} &\eta_i(v_1^{(n_0)}(u))\\ &\quad= \begin{cases} \dfrac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2} {4096} &\textrm{ if }\ d(u, y_i) \leq \dfrac {s\delta} 2,\\\\[-6pt] \dfrac {(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\|)^2}{4096}&\\\\[-6pt] \qquad\cdot\exp\bigg(1 + \dfrac{1}{( (1/ {s\delta})\, d(u,y_i) - ( 1/ 2) )^2 - 1}\bigg) &\textrm{ if }\ \dfrac {s\delta} 2 < d(u,y_i) < s\delta,\\ 0 &\textrm{ if }\ s\delta \leq d(u,y_i), \end{cases} \end{align*} $$
for all
![]() $u \in B_{\delta }(x_i)$
. We can smoothly extend
$u \in B_{\delta }(x_i)$
. We can smoothly extend
![]() $\eta _i$
to all of U by setting
$\eta _i$
to all of U by setting
![]() $\eta _i = 0$
outside
$\eta _i = 0$
outside
 $v_1^{(n_0)}(u)( B_{\delta }(x_i) )$
. To define
$v_1^{(n_0)}(u)( B_{\delta }(x_i) )$
. To define
![]() $\beta $
, we simply set
$\beta $
, we simply set
 $$ \begin{align*} \beta(u) := 1 - \sum_i \eta_i(u) \end{align*} $$
$$ \begin{align*} \beta(u) := 1 - \sum_i \eta_i(u) \end{align*} $$
and by Lemma 5.4 we clearly have
 $$ \begin{align*} \| ( \mathcal L^{n_0}_{z,\rho} \varphi )(u) \|_{L^2(G)} \leq ( \mathcal L^{n_0}_{\mathrm{Re}(z),0} ( \beta \Phi ) )(u) \end{align*} $$
$$ \begin{align*} \| ( \mathcal L^{n_0}_{z,\rho} \varphi )(u) \|_{L^2(G)} \leq ( \mathcal L^{n_0}_{\mathrm{Re}(z),0} ( \beta \Phi ) )(u) \end{align*} $$
for all
![]() $u \in U$
. It simply remains to estimate
$u \in U$
. It simply remains to estimate
 $\|\mathcal L^{n_0}_{P(\varsigma ),0} ( \beta \Phi ) \|_{L^2(\nu ^u)}$
.
$\|\mathcal L^{n_0}_{P(\varsigma ),0} ( \beta \Phi ) \|_{L^2(\nu ^u)}$
.
In principle, we have only introduced contraction into a single term in
 $\mathcal L^{n_0}_{P(\varsigma ),0} (\beta \Phi )$
at any given point; we need to argue that this was significant enough for our purposes. The regularity of
$\mathcal L^{n_0}_{P(\varsigma ),0} (\beta \Phi )$
at any given point; we need to argue that this was significant enough for our purposes. The regularity of
![]() $\Phi $
is essential here. As in (5.1), note that the ratio between
$\Phi $
is essential here. As in (5.1), note that the ratio between
 $\Phi (v^{(n_0)}_a(u))$
and
$\Phi (v^{(n_0)}_a(u))$
and
 $\Phi (v^{(n_0)}_b(u))$
cannot exceed
$\Phi (v^{(n_0)}_b(u))$
cannot exceed
 $$ \begin{align*} \frac{\Phi(v^{(n_0)}_a(u))}{\Phi(v^{(n_0)}_b(u))} \leq e^{ (C/ f) \operatorname{\mathrm{diam}}(N)} \end{align*} $$
$$ \begin{align*} \frac{\Phi(v^{(n_0)}_a(u))}{\Phi(v^{(n_0)}_b(u))} \leq e^{ (C/ f) \operatorname{\mathrm{diam}}(N)} \end{align*} $$
for any pair of pasts
![]() $v_a, v_b$
. As a consequence, we must have
$v_a, v_b$
. As a consequence, we must have
 $$ \begin{align} \frac{(\epsilon \delta (1+|\mathrm{Im}(z)|)\|\rho\|)^2}{4096 (\ell_0e^{ (C/ f) \operatorname{\mathrm{diam}}(N)}) } \sum_{v_a^{(n_0)}} \Phi( v_a^{(n_0)} (u) )\leq \frac{(\epsilon \delta (1+|\mathrm{Im}(z)|)\|\rho\|)^2}{4096} \Phi(v_{1,i}^{(n_0)}(u)) \end{align} $$
$$ \begin{align} \frac{(\epsilon \delta (1+|\mathrm{Im}(z)|)\|\rho\|)^2}{4096 (\ell_0e^{ (C/ f) \operatorname{\mathrm{diam}}(N)}) } \sum_{v_a^{(n_0)}} \Phi( v_a^{(n_0)} (u) )\leq \frac{(\epsilon \delta (1+|\mathrm{Im}(z)|)\|\rho\|)^2}{4096} \Phi(v_{1,i}^{(n_0)}(u)) \end{align} $$
where
![]() $\ell _0$
is the number of pasts
$\ell _0$
is the number of pasts
 $v_a^{(n_0)}$
of length
$v_a^{(n_0)}$
of length
![]() $n_0$
, and the sum is taken over all such pasts. Of course, we can find a uniform
$n_0$
, and the sum is taken over all such pasts. Of course, we can find a uniform
![]() $D> 0$
so that
$D> 0$
so that
 $D^{-1} \leq e^{\alpha ^{(n_0)}_{\mathrm {Re}(z)}( v_{a}^{(n_0)}(u) )} \leq D$
for all pasts and all
$D^{-1} \leq e^{\alpha ^{(n_0)}_{\mathrm {Re}(z)}( v_{a}^{(n_0)}(u) )} \leq D$
for all pasts and all
![]() $u \in U$
; note that D can be chosen independently of z so long as we require
$u \in U$
; note that D can be chosen independently of z so long as we require
![]() $|\mathrm {Re}(z) - P(\varsigma )| < 1$
. From this, we can bound
$|\mathrm {Re}(z) - P(\varsigma )| < 1$
. From this, we can bound
 $$ \begin{align*} &\frac{(\epsilon \delta (1+|\mathrm{Im}(z)|)\|\rho\|)^2}{4096 D^2(\ell_0e^{(C/ f) \operatorname{\mathrm{diam}}(N)}) } \sum_{v_a^{(n_0)}} e^{\alpha^{(n_0)}_{\mathrm{Re}(z)}( v_{a}^{(n_0)}(u) )} \Phi( v_a^{(n_0)}(u) )\\ &\quad\leq \frac{(\epsilon \delta (1+|\mathrm{Im}(z)|)\|\rho\|)^2}{4096} e^{\alpha^{(n_0)}_{\mathrm{Re}(z)}( v_{1,i}^{(n_0)}(u) )} \Phi(v_{1,i}^{(n_0)}(u)) \end{align*} $$
$$ \begin{align*} &\frac{(\epsilon \delta (1+|\mathrm{Im}(z)|)\|\rho\|)^2}{4096 D^2(\ell_0e^{(C/ f) \operatorname{\mathrm{diam}}(N)}) } \sum_{v_a^{(n_0)}} e^{\alpha^{(n_0)}_{\mathrm{Re}(z)}( v_{a}^{(n_0)}(u) )} \Phi( v_a^{(n_0)}(u) )\\ &\quad\leq \frac{(\epsilon \delta (1+|\mathrm{Im}(z)|)\|\rho\|)^2}{4096} e^{\alpha^{(n_0)}_{\mathrm{Re}(z)}( v_{1,i}^{(n_0)}(u) )} \Phi(v_{1,i}^{(n_0)}(u)) \end{align*} $$
following (5.25). This leads immediately to obtaining the pointwise bound
 $$ \begin{align*} (\mathcal L^{n_0}_{P(\varsigma),0} ( \beta \Phi )) (u) \leq \bigg( 1 - \frac {( \epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2} {4096D^2(\ell_0 e^{(C/ f) \operatorname{\mathrm{diam}}(N)})} \bigg) (\mathcal L^{n_0}_{P(\varsigma),0} \Phi )(u) \end{align*} $$
$$ \begin{align*} (\mathcal L^{n_0}_{P(\varsigma),0} ( \beta \Phi )) (u) \leq \bigg( 1 - \frac {( \epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2} {4096D^2(\ell_0 e^{(C/ f) \operatorname{\mathrm{diam}}(N)})} \bigg) (\mathcal L^{n_0}_{P(\varsigma),0} \Phi )(u) \end{align*} $$
for all
![]() $u \in \bigcup B_{ {s\delta }/ 2}(y_i)$
by construction. On the other hand, because
$u \in \bigcup B_{ {s\delta }/ 2}(y_i)$
by construction. On the other hand, because
 $\mathcal L^{n_0}_{P(\varsigma ),0}$
is monotonic, we of course have
$\mathcal L^{n_0}_{P(\varsigma ),0}$
is monotonic, we of course have
 $$ \begin{align*} (\mathcal L^{n_0}_{P(\varsigma),0} ( \beta \Phi )) (u) \leq (\mathcal L^{n_0}_{P(\varsigma),0} \Phi )(u) \end{align*} $$
$$ \begin{align*} (\mathcal L^{n_0}_{P(\varsigma),0} ( \beta \Phi )) (u) \leq (\mathcal L^{n_0}_{P(\varsigma),0} \Phi )(u) \end{align*} $$
for all
![]() $u \in U - \bigcup B_{{s\delta }/2}(y_i)$
. Taken together, these inequalities mean that we can bound
$u \in U - \bigcup B_{{s\delta }/2}(y_i)$
. Taken together, these inequalities mean that we can bound
 $$ \begin{align*} \|(\mathcal L^{n_0}_{P(\varsigma),0} ( \beta \Phi )) \|_{L^2(\nu^u)} \end{align*} $$
$$ \begin{align*} \|(\mathcal L^{n_0}_{P(\varsigma),0} ( \beta \Phi )) \|_{L^2(\nu^u)} \end{align*} $$
from above by
 $$ \begin{align*} &\bigg(\int_{\bigcup B_{ {s\delta}/ 2}(y_i)} \bigg( 1 - \frac {( \epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2} {4096D^2(\ell_0 e^{(C/ f) \operatorname{\mathrm{diam}}(N)})} \bigg)^2 ((\mathcal L^{n_0}_{P(\varsigma),0} \Phi )(u))^2 d\nu^u \bigg)^{1/ 2}\\ &\quad+\, \bigg(\int_{U - \bigcup B_{{s\delta}/ 2}(y_i)} ((\mathcal L^{n_0}_{P(\varsigma),0} \Phi )(u))^2 d\nu^u \bigg)^{ 1 /2} \end{align*} $$
$$ \begin{align*} &\bigg(\int_{\bigcup B_{ {s\delta}/ 2}(y_i)} \bigg( 1 - \frac {( \epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2} {4096D^2(\ell_0 e^{(C/ f) \operatorname{\mathrm{diam}}(N)})} \bigg)^2 ((\mathcal L^{n_0}_{P(\varsigma),0} \Phi )(u))^2 d\nu^u \bigg)^{1/ 2}\\ &\quad+\, \bigg(\int_{U - \bigcup B_{{s\delta}/ 2}(y_i)} ((\mathcal L^{n_0}_{P(\varsigma),0} \Phi )(u))^2 d\nu^u \bigg)^{ 1 /2} \end{align*} $$
for our particular choice of
![]() $\rho $
and z. As the operator
$\rho $
and z. As the operator
 $\mathcal L^{n_0}_{P(\varsigma ),0}$
preserves the measure
$\mathcal L^{n_0}_{P(\varsigma ),0}$
preserves the measure
![]() $\nu ^u$
(by our renormalization), this is exactly
$\nu ^u$
(by our renormalization), this is exactly
 $$ \begin{align*} \| \Phi \|_{L^2(\nu^u)}\bigg( 1 - \frac{(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2} {4096D^2(\ell_0 e^{(C /f) \operatorname{\mathrm{diam}}(N)})} \nu^u\bigg( \bigcup B_{ {s\delta}/2}(y_i)\bigg) \bigg). \end{align*} $$
$$ \begin{align*} \| \Phi \|_{L^2(\nu^u)}\bigg( 1 - \frac{(\epsilon \delta (1+|\mathrm{Im}(z)|) \|\rho\| )^2} {4096D^2(\ell_0 e^{(C /f) \operatorname{\mathrm{diam}}(N)})} \nu^u\bigg( \bigcup B_{ {s\delta}/2}(y_i)\bigg) \bigg). \end{align*} $$
By the diametric regularity of the measure
![]() $\nu ^u$
, there is a uniform constant
$\nu ^u$
, there is a uniform constant
![]() $r < 1$
for which
$r < 1$
for which
for all i. Hence, we have
 $$ \begin{align*} \nu^u \bigg( \bigcup B_{ {s\delta}/2}(y_i) \bigg) \geq r \nu^u \bigg( \bigcup B_{3\delta}(y_i) \bigg) \geq r \nu^u ( U_{lni} ), \end{align*} $$
$$ \begin{align*} \nu^u \bigg( \bigcup B_{ {s\delta}/2}(y_i) \bigg) \geq r \nu^u \bigg( \bigcup B_{3\delta}(y_i) \bigg) \geq r \nu^u ( U_{lni} ), \end{align*} $$
completing the proof.
It is important to recognize that many of the estimates so far do, in fact, depend on
![]() $\rho $
,
$\rho $
,
![]() $\mathrm {Im}(z)$
or C; this is problematic for the spectral bounds we want to obtain. To isolate some of these dependencies, we restrict our attention to control functions
$\mathrm {Im}(z)$
or C; this is problematic for the spectral bounds we want to obtain. To isolate some of these dependencies, we restrict our attention to control functions
![]() $\Phi \in \mathcal K_{C (1+|\mathrm {Im}(z)|) \|\rho \| }$
, where we hope to be able to make a uniform choice of an appropriate C. In particular, we want to find a C so that
$\Phi \in \mathcal K_{C (1+|\mathrm {Im}(z)|) \|\rho \| }$
, where we hope to be able to make a uniform choice of an appropriate C. In particular, we want to find a C so that
![]() $\mathcal K_{C (1+|\mathrm {Im}(z)|) \|\rho \|}$
is invariant under
$\mathcal K_{C (1+|\mathrm {Im}(z)|) \|\rho \|}$
is invariant under
![]() $\mathcal L^n_{z,\rho }$
, at least for z with
$\mathcal L^n_{z,\rho }$
, at least for z with
![]() $\mathrm {Re}(z)$
sufficiently close to
$\mathrm {Re}(z)$
sufficiently close to
![]() $P(\varsigma )$
.
$P(\varsigma )$
.
Proposition 5.6. There is a uniform choice of constant
![]() $C> 0$
so that, for all
$C> 0$
so that, for all
![]() $\varphi \in C^1(U, V^\rho )$
and
$\varphi \in C^1(U, V^\rho )$
and
![]() $\Phi \in \mathcal K_{C(1+|\mathrm {Im}(z)|\|\rho \|}$
, if we have
$\Phi \in \mathcal K_{C(1+|\mathrm {Im}(z)|\|\rho \|}$
, if we have
 $$ \begin{align*} \| \varphi(u) \|_{L^2(G)} &\leq \Phi(u),\\[3pt] \sup_{w \in T^1_uU} \| (d\varphi)_u(w) \|_{L^2(G)} &\leq C(1+|\mathrm{Im}(z)|)\Phi(u) \end{align*} $$
$$ \begin{align*} \| \varphi(u) \|_{L^2(G)} &\leq \Phi(u),\\[3pt] \sup_{w \in T^1_uU} \| (d\varphi)_u(w) \|_{L^2(G)} &\leq C(1+|\mathrm{Im}(z)|)\Phi(u) \end{align*} $$
for all
![]() $u \in U$
, then we can bound
$u \in U$
, then we can bound
 $$ \begin{align*} \sup_{w \in T^1_uU} \| (d( \mathcal L^n_{z,\rho}\varphi ))_u(w) \|_{L^2(G)} \leq C (1+|\mathrm{Im}(z)|)\|\rho\| (\mathcal L_{\mathrm{Re}(z),0}^n \Phi)(u) \end{align*} $$
$$ \begin{align*} \sup_{w \in T^1_uU} \| (d( \mathcal L^n_{z,\rho}\varphi ))_u(w) \|_{L^2(G)} \leq C (1+|\mathrm{Im}(z)|)\|\rho\| (\mathcal L_{\mathrm{Re}(z),0}^n \Phi)(u) \end{align*} $$
for all
![]() $u \in U$
, and all
$u \in U$
, and all
![]() $n> 0$
.
$n> 0$
.
Proof. Fix
![]() $u \in U$
. By definition, the transfer operator can be expressed as the sum
$u \in U$
. By definition, the transfer operator can be expressed as the sum
 $$ \begin{align} ( \mathcal L^n_{z,\rho}\varphi )(u) = \sum_{i} e^{\alpha_{z}^{(n)}(v_i^{(n)}(u))} \rho( \operatorname{\mathrm{Hol}}^{(n)}(v_i^{(n)}(u)) ) \varphi( v_i^{(n)}(u) ) \end{align} $$
$$ \begin{align} ( \mathcal L^n_{z,\rho}\varphi )(u) = \sum_{i} e^{\alpha_{z}^{(n)}(v_i^{(n)}(u))} \rho( \operatorname{\mathrm{Hol}}^{(n)}(v_i^{(n)}(u)) ) \varphi( v_i^{(n)}(u) ) \end{align} $$
over pasts
 $v_i^{(n)}$
. We need to control
$v_i^{(n)}$
. We need to control
 $$ \begin{align*} \sup_{w \in T^1_uU} \| d( \mathcal L_{z,\rho}^n(\varphi) )_u(w)\|_{L^2(G)}, \end{align*} $$
$$ \begin{align*} \sup_{w \in T^1_uU} \| d( \mathcal L_{z,\rho}^n(\varphi) )_u(w)\|_{L^2(G)}, \end{align*} $$
which we will accomplish by differentiating (5.26) term-by-term. For a fixed i, the derivative
 $$ \begin{align*} d(e^{\alpha_{z}^{(n)}(v_i^{(n)}(u))} \rho( \operatorname{\mathrm{Hol}}^{(n)}(v_i^{(n)}(u)) ) \varphi( v_i^{(n)}(u) ))_u(w) \end{align*} $$
$$ \begin{align*} d(e^{\alpha_{z}^{(n)}(v_i^{(n)}(u))} \rho( \operatorname{\mathrm{Hol}}^{(n)}(v_i^{(n)}(u)) ) \varphi( v_i^{(n)}(u) ))_u(w) \end{align*} $$
can be bounded by the sum
 $$ \begin{align} &\|e^{\alpha_{z}^{(n)}( v_i^{(n)}(u) )}(\rho( \operatorname{\mathrm{Hol}}^{(n)}( v_i^{(n)}(u) ) )\varphi( v_i^{(n)}(u) ) ) ( d( \alpha_{z}^{(n)} \circ v_i^{(n)}) )_u(w)\|_{L^2(G)} \end{align} $$
$$ \begin{align} &\|e^{\alpha_{z}^{(n)}( v_i^{(n)}(u) )}(\rho( \operatorname{\mathrm{Hol}}^{(n)}( v_i^{(n)}(u) ) )\varphi( v_i^{(n)}(u) ) ) ( d( \alpha_{z}^{(n)} \circ v_i^{(n)}) )_u(w)\|_{L^2(G)} \end{align} $$
 $$ \begin{align} & \kern-35pt + \|e^{\alpha_{z}^{(n)}( v_i^{(n)}(u) )}((d( \rho( \operatorname{\mathrm{Hol}}^{(n)} \circ v_i^{(n)} )))_u(w)) \varphi( v_i^{(n)}(u) )\|_{L^2(G)} \end{align} $$
$$ \begin{align} & \kern-35pt + \|e^{\alpha_{z}^{(n)}( v_i^{(n)}(u) )}((d( \rho( \operatorname{\mathrm{Hol}}^{(n)} \circ v_i^{(n)} )))_u(w)) \varphi( v_i^{(n)}(u) )\|_{L^2(G)} \end{align} $$
 $$ \begin{align} & \kern-40pt + \|e^{\alpha_{z}^{(n)}( v_i^{(n)}(u) )}\rho( \operatorname{\mathrm{Hol}}^{(n)}( v_i^{(n)}(u) ) ) (d (\varphi \circ v_i^{(n)} ) )_u(w) \|_{L^2(G)} \end{align} $$
$$ \begin{align} & \kern-40pt + \|e^{\alpha_{z}^{(n)}( v_i^{(n)}(u) )}\rho( \operatorname{\mathrm{Hol}}^{(n)}( v_i^{(n)}(u) ) ) (d (\varphi \circ v_i^{(n)} ) )_u(w) \|_{L^2(G)} \end{align} $$
for all
![]() $w \in T^1_uU$
. We bound each of these terms individually, beginning with (5.27). Observe that
$w \in T^1_uU$
. We bound each of these terms individually, beginning with (5.27). Observe that

and so (5.27) is at most

for all
![]() $u \in U$
and
$u \in U$
and
![]() $w \in T^1_uU$
. Exactly the same calculations show us that
$w \in T^1_uU$
. Exactly the same calculations show us that

and, hence, that (5.28) is at most

by the definition of
![]() $\|\rho \|$
and the chain rule. Finally, we can bound (5.29) by
$\|\rho \|$
and the chain rule. Finally, we can bound (5.29) by
 $$ \begin{align*} \frac{C(1+|\mathrm{Im}(z)|)\|\rho\|}{f\kappa^n} e^{\alpha_{\mathrm{Re}(z)}( v_i^{(n)}(u) )} \Phi( v_i^{(n)}(u) ) \end{align*} $$
$$ \begin{align*} \frac{C(1+|\mathrm{Im}(z)|)\|\rho\|}{f\kappa^n} e^{\alpha_{\mathrm{Re}(z)}( v_i^{(n)}(u) )} \Phi( v_i^{(n)}(u) ) \end{align*} $$
by hypothesis. Combining all of these with the pointwise bound on the norm of
![]() $\varphi $
, we see that so long as we have
$\varphi $
, we see that so long as we have

we obtain the bounds desired. Note that
![]() $\|\operatorname {\mathrm {Hol}}\|_{C^1}$
is a uniform constant and
$\|\operatorname {\mathrm {Hol}}\|_{C^1}$
is a uniform constant and
![]() $\|\alpha _z\|_{C^1}$
is at most
$\|\alpha _z\|_{C^1}$
is at most
![]() $\|\alpha _{\mathrm {Re}(z)}\|_{C^1} (1 + |\mathrm {Im}(z)|)$
. As
$\|\alpha _{\mathrm {Re}(z)}\|_{C^1} (1 + |\mathrm {Im}(z)|)$
. As
![]() $\|\alpha _{\mathrm {Re}(z)}\|_{C^1}$
is uniformly bounded when
$\|\alpha _{\mathrm {Re}(z)}\|_{C^1}$
is uniformly bounded when
![]() $\mathrm {Re}(z)$
is confined to the bounded interval
$\mathrm {Re}(z)$
is confined to the bounded interval
![]() $|\mathrm {Re}(z) - P(\varsigma )| < 1$
, we can clearly choose a
$|\mathrm {Re}(z) - P(\varsigma )| < 1$
, we can clearly choose a
![]() $C> 0$
so that (5.30) holds for all
$C> 0$
so that (5.30) holds for all
![]() $n> 0$
.
$n> 0$
.
We are now in a position to prove Theorem 3.2; the strategy is entirely analogous to that outlined in [Reference Dolgopyat11, §6] or [Reference Sharp17, Theorem 6.8].
Theorem 5.7. Fix a non-trivial isotypic representation
![]() $\rho> 0$
and
$\rho> 0$
and
![]() $z \in \mathbb {C}$
with
$z \in \mathbb {C}$
with
![]() $|\mathrm {Re}(z) - P(\varsigma )| < 1$
. There are uniform constants
$|\mathrm {Re}(z) - P(\varsigma )| < 1$
. There are uniform constants
![]() $D> 0$
and
$D> 0$
and
![]() $r_0 < 1$
so that
$r_0 < 1$
so that
for all
![]() $\varphi \in C^1(U, V^\rho )$
. Neither D nor
$\varphi \in C^1(U, V^\rho )$
. Neither D nor
![]() $r_0$
depends on
$r_0$
depends on
![]() $\rho $
,
$\rho $
,
![]() $\varphi $
or z.
$\varphi $
or z.
Proof. Fix
![]() $C> 0$
,
$C> 0$
,
![]() $N> 0$
as in Lemma 5.6 and
$N> 0$
as in Lemma 5.6 and
![]() $n_0> N$
as in Lemma 5.5. We begin by setting
$n_0> N$
as in Lemma 5.5. We begin by setting
 $$ \begin{align*} \varphi_0(u) &:= \varphi(u),\\ \Phi_0(u) &:= \|\varphi\|_{C^1} \end{align*} $$
$$ \begin{align*} \varphi_0(u) &:= \varphi(u),\\ \Phi_0(u) &:= \|\varphi\|_{C^1} \end{align*} $$
for which we clearly have
![]() $\Phi _0 \in \mathcal K_{C (1 + |\mathrm {Im}(z)|) \|\rho \|}$
as well as the bounds
$\Phi _0 \in \mathcal K_{C (1 + |\mathrm {Im}(z)|) \|\rho \|}$
as well as the bounds
 $$ \begin{align*} \| \varphi_0(u) \|_{L^2(G)} &\leq \Phi_0(u),\\ \sup_{w \in T^1_uU} \| (d\varphi_0 )_u (w) \|_{L^2(G)} &\leq C (1+|\mathrm{Im}(z)|) \|\rho\| \Phi_0(u) \end{align*} $$
$$ \begin{align*} \| \varphi_0(u) \|_{L^2(G)} &\leq \Phi_0(u),\\ \sup_{w \in T^1_uU} \| (d\varphi_0 )_u (w) \|_{L^2(G)} &\leq C (1+|\mathrm{Im}(z)|) \|\rho\| \Phi_0(u) \end{align*} $$
assuming that
![]() $C> 0$
is large enough so that
$C> 0$
is large enough so that
![]() $C\|\rho \|> 1$
for all
$C\|\rho \|> 1$
for all
![]() $\rho $
. By Lemma 5.5, we can find a function
$\rho $
. By Lemma 5.5, we can find a function
![]() $\beta _0 \in C^1(U, \mathbb {R})$
for which we have
$\beta _0 \in C^1(U, \mathbb {R})$
for which we have
 $$ \begin{align*} \| ( \mathcal L^{n_0}_{z,\rho} \varphi_0 )(u) \|_{L^2(G)} \leq ( \mathcal L^{n_0}_{\mathrm{Re}(z),0} ( \beta_0 \Phi_0 ) )(u) \end{align*} $$
$$ \begin{align*} \| ( \mathcal L^{n_0}_{z,\rho} \varphi_0 )(u) \|_{L^2(G)} \leq ( \mathcal L^{n_0}_{\mathrm{Re}(z),0} ( \beta_0 \Phi_0 ) )(u) \end{align*} $$
and
 $$ \begin{align*} \| \mathcal L_{\mathrm{Re}(z),0}^{n_0} ( \beta_0 \Phi_0 ) \|_{L^2(\nu^u)} \leq r_0 \| \Phi_0\|_{L^2(\nu^u)} \end{align*} $$
$$ \begin{align*} \| \mathcal L_{\mathrm{Re}(z),0}^{n_0} ( \beta_0 \Phi_0 ) \|_{L^2(\nu^u)} \leq r_0 \| \Phi_0\|_{L^2(\nu^u)} \end{align*} $$
for a uniform choice of
![]() $n_0> 0$
. Moreover,
$n_0> 0$
. Moreover,
![]() $r_0$
and
$r_0$
and
![]() $\|\beta _0\|_{C^1}$
can be made uniform in
$\|\beta _0\|_{C^1}$
can be made uniform in
![]() $\rho , \varphi $
and z by choosing
$\rho , \varphi $
and z by choosing
![]() $\delta $
so that
$\delta $
so that
![]() $C(1+|\mathrm {Im}(z)|)\|\rho \| \cdot \delta $
is constant, as in Lemma 5.1.
$C(1+|\mathrm {Im}(z)|)\|\rho \| \cdot \delta $
is constant, as in Lemma 5.1.
We want to iterate this, for which it will be crucial that we can find a uniform
![]() $C_0$
so that we have
$C_0$
so that we have
![]() $\beta _0 \Phi _0 \in \mathcal K_{C_0(1+|\mathrm {Im}(z)|)\|\rho \|}$
for all
$\beta _0 \Phi _0 \in \mathcal K_{C_0(1+|\mathrm {Im}(z)|)\|\rho \|}$
for all
![]() $\Phi _0 \in \mathcal K_{C_0(1+|\mathrm {Im}(z)|)\|\rho \|}$
. For any given
$\Phi _0 \in \mathcal K_{C_0(1+|\mathrm {Im}(z)|)\|\rho \|}$
. For any given
![]() $\Phi _0 \in \mathcal K_{C(1+|\mathrm {Im}(z)|)\|\rho \|}$
, we have
$\Phi _0 \in \mathcal K_{C(1+|\mathrm {Im}(z)|)\|\rho \|}$
, we have
 $$ \begin{align*} \sup_{w \in T^1_uU} |(d(\Phi_0\beta_0)_u (w) | &\leq \beta_0(u) (\sup_{w \in T^1_uU} |(d\Phi_0)_u(w)| ) + \Phi_0(u) ( \sup_{w \in T^1_uU} |(d\beta_0)_u(w)| )\\ &\leq \sup_{w\in T^1_uU} \Phi_0(u) ( C(1+ |\mathrm{Im}(z)|)\|\rho\| \beta_0(u) + (d\beta_0)_u(w) ) \end{align*} $$
$$ \begin{align*} \sup_{w \in T^1_uU} |(d(\Phi_0\beta_0)_u (w) | &\leq \beta_0(u) (\sup_{w \in T^1_uU} |(d\Phi_0)_u(w)| ) + \Phi_0(u) ( \sup_{w \in T^1_uU} |(d\beta_0)_u(w)| )\\ &\leq \sup_{w\in T^1_uU} \Phi_0(u) ( C(1+ |\mathrm{Im}(z)|)\|\rho\| \beta_0(u) + (d\beta_0)_u(w) ) \end{align*} $$
for all
![]() $u \in U$
. From the construction of
$u \in U$
. From the construction of
![]() $\beta _0$
, and by our earlier remarks on our choice of
$\beta _0$
, and by our earlier remarks on our choice of
![]() $\delta $
, it is clear that we can choose a uniform
$\delta $
, it is clear that we can choose a uniform
![]() $C_0$
large enough so that
$C_0$
large enough so that
 $$ \begin{align*} \sup_{w\in T^1_uU} C(1+ |\mathrm{Im}(z)|)\|\rho\| \beta_0(u) + (d\beta_0)_u(w) \leq C_0 \beta_0(u) \end{align*} $$
$$ \begin{align*} \sup_{w\in T^1_uU} C(1+ |\mathrm{Im}(z)|)\|\rho\| \beta_0(u) + (d\beta_0)_u(w) \leq C_0 \beta_0(u) \end{align*} $$
for any choice of
![]() $\beta _0$
as in Lemma 5.5. We then clearly have
$\beta _0$
as in Lemma 5.5. We then clearly have
![]() $\beta _0 \Phi _0 \in \mathcal K_{C_0 (1+|\mathrm {Im}(z)|) \|\rho \|}$
, and, hence, by Lemma 5.6 we obtain
$\beta _0 \Phi _0 \in \mathcal K_{C_0 (1+|\mathrm {Im}(z)|) \|\rho \|}$
, and, hence, by Lemma 5.6 we obtain
 $$ \begin{align*} \sup_{w \in T^1_uU} \| (d(\mathcal L^{n_0}_{z,\rho}\varphi))_u(w) \|_{L^2(G)} \leq C_0 (1+|\mathrm{Im}(z)|) \|\rho\| ( \mathcal L^n_{\mathrm{Re}(z),0} \Phi_0 )(u) \end{align*} $$
$$ \begin{align*} \sup_{w \in T^1_uU} \| (d(\mathcal L^{n_0}_{z,\rho}\varphi))_u(w) \|_{L^2(G)} \leq C_0 (1+|\mathrm{Im}(z)|) \|\rho\| ( \mathcal L^n_{\mathrm{Re}(z),0} \Phi_0 )(u) \end{align*} $$
for all
![]() $u \in U$
.
$u \in U$
.
Now, we can repeat what we have done so far and inductively choose
![]() $\beta _{i-1}$
as in Lemma 5.5, setting
$\beta _{i-1}$
as in Lemma 5.5, setting
 $$ \begin{align*} \varphi_i(u) &:= (\mathcal L_{z,\rho}^{n_0} \varphi_{i-1} )(u),\\ \Phi_i(u) &:= ( \mathcal L_{\mathrm{Re}(z),0}^{n_0} (\beta_{i-1} \Phi_{i-1} ))(u) \end{align*} $$
$$ \begin{align*} \varphi_i(u) &:= (\mathcal L_{z,\rho}^{n_0} \varphi_{i-1} )(u),\\ \Phi_i(u) &:= ( \mathcal L_{\mathrm{Re}(z),0}^{n_0} (\beta_{i-1} \Phi_{i-1} ))(u) \end{align*} $$
for
![]() $i \geq 1$
. Note that we have just shown that
$i \geq 1$
. Note that we have just shown that
![]() $\Phi _1 \in \mathcal K_{C_0(1 + |\mathrm {Im}(z)|)\|\rho \|}$
and that we have
$\Phi _1 \in \mathcal K_{C_0(1 + |\mathrm {Im}(z)|)\|\rho \|}$
and that we have
 $$ \begin{align*} \| \varphi_1(u) \|_{L^2(G)} &\leq \Phi_1(u),\\ \sup_{w \in T^1_uU} \| (d\varphi_1 )_u (w) \|_{L^2(G)} &\leq C_0 (1 + |\mathrm{Im}(z)|) \|\rho\| \Phi_1(u) \end{align*} $$
$$ \begin{align*} \| \varphi_1(u) \|_{L^2(G)} &\leq \Phi_1(u),\\ \sup_{w \in T^1_uU} \| (d\varphi_1 )_u (w) \|_{L^2(G)} &\leq C_0 (1 + |\mathrm{Im}(z)|) \|\rho\| \Phi_1(u) \end{align*} $$
for all
![]() $u \in U$
. As before, we obtain
$u \in U$
. As before, we obtain
 $$ \begin{align*} \| \varphi_i(u) \|_{L^2(G)} &\leq \Phi_i(u),\\ \sup_{w \in T^1_uU} \| (d\varphi_i )_u (w) \|_{L^2(G)} &\leq C_0 (1 + |\mathrm{Im}(z)|) \|\rho\| \Phi_i(u) \end{align*} $$
$$ \begin{align*} \| \varphi_i(u) \|_{L^2(G)} &\leq \Phi_i(u),\\ \sup_{w \in T^1_uU} \| (d\varphi_i )_u (w) \|_{L^2(G)} &\leq C_0 (1 + |\mathrm{Im}(z)|) \|\rho\| \Phi_i(u) \end{align*} $$
inductively for all
![]() $i \geq 1$
and, moreover,
$i \geq 1$
and, moreover,
by construction. Chaining these inequalities together, we have
 $$ \begin{align*} \|\mathcal L^{i \cdot n_0}_{z,\rho} \varphi \|_{L^2(\nu^u)} \leq r_0^i \|\varphi \|_{C^1}, \end{align*} $$
$$ \begin{align*} \|\mathcal L^{i \cdot n_0}_{z,\rho} \varphi \|_{L^2(\nu^u)} \leq r_0^i \|\varphi \|_{C^1}, \end{align*} $$
which is almost what we need. To conclude, observe that we have
 $$ \begin{align*} \|( \mathcal L^{i \cdot n_0 + k}_{z,\rho} \varphi )(u) \|_{L^2(\nu^u)} \leq r_0^i \|\varphi \|_{C^1} \| \mathcal L_{z,\rho}^k\|_{L^2(G)}, \end{align*} $$
$$ \begin{align*} \|( \mathcal L^{i \cdot n_0 + k}_{z,\rho} \varphi )(u) \|_{L^2(\nu^u)} \leq r_0^i \|\varphi \|_{C^1} \| \mathcal L_{z,\rho}^k\|_{L^2(G)}, \end{align*} $$
where
 $\| \mathcal L_{z,\rho }^k \|_{L^2(G)}$
denotes the operator norm of
$\| \mathcal L_{z,\rho }^k \|_{L^2(G)}$
denotes the operator norm of
 $\mathcal L_{z,\rho }^k$
. If
$\mathcal L_{z,\rho }^k$
. If
![]() $k < n_0$
and
$k < n_0$
and
![]() $|\mathrm {Re}(z) - P(\varsigma )| \, < 1$
, then we can find a uniform bound
$|\mathrm {Re}(z) - P(\varsigma )| \, < 1$
, then we can find a uniform bound
![]() $D> 0$
so that
$D> 0$
so that
 $\|\mathcal L_{z,\rho }^k \|_{L^2(G)} \leq D$
, as desired.
$\|\mathcal L_{z,\rho }^k \|_{L^2(G)} \leq D$
, as desired.
The differentiability of the potential
![]() $\varsigma $
was essential to much of what we have done so far in this section; to extend our results to the case when
$\varsigma $
was essential to much of what we have done so far in this section; to extend our results to the case when
![]() $\varsigma $
is only Hölder, however, is a relatively straightforward approximation argument, identical to that given in [Reference Dolgopyat11, §4(II)]. We sketch this in the following.
$\varsigma $
is only Hölder, however, is a relatively straightforward approximation argument, identical to that given in [Reference Dolgopyat11, §4(II)]. We sketch this in the following.
Corollary 5.8. With notation as in Theorem 5.7, we have
 $$ \begin{align*} \|\mathcal L^n_{\mathrm{Re}(z),\rho} \varphi \|_{L^2(\nu^u)} \leq Dr_0^n\|\varphi\|_{C^1} \end{align*} $$
$$ \begin{align*} \|\mathcal L^n_{\mathrm{Re}(z),\rho} \varphi \|_{L^2(\nu^u)} \leq Dr_0^n\|\varphi\|_{C^1} \end{align*} $$
when the potential
![]() $\varsigma $
is only Hölder continuous.
$\varsigma $
is only Hölder continuous.
Proof. Suppose that
![]() $\varsigma $
is Hölder continuous. As in [Reference Dolgopyat11], we can find a sequence of smooth potentials
$\varsigma $
is Hölder continuous. As in [Reference Dolgopyat11], we can find a sequence of smooth potentials
![]() $\varsigma ^{(\mathrm {Im}(z))} \in C^1(U, \mathbb {R})$
indexed by
$\varsigma ^{(\mathrm {Im}(z))} \in C^1(U, \mathbb {R})$
indexed by
![]() $\mathrm {Im}(z)$
for which we have
$\mathrm {Im}(z)$
for which we have
 $$ \begin{align} \sup_{u \in U} | \varsigma_0(u) - \varsigma^{(\mathrm{Im}(z))}(u) | \leq \|\varsigma_0\|_{C^\alpha} \bigg( \frac 1 {|\mathrm{Im}(z)|} \bigg)^{\alpha/2} \end{align} $$
$$ \begin{align} \sup_{u \in U} | \varsigma_0(u) - \varsigma^{(\mathrm{Im}(z))}(u) | \leq \|\varsigma_0\|_{C^\alpha} \bigg( \frac 1 {|\mathrm{Im}(z)|} \bigg)^{\alpha/2} \end{align} $$
and
 $$ \begin{align} \|\varsigma^{(\mathrm{Im}(z))}\|_{C^1} < C\sqrt{|\mathrm{Im}(z)|} \end{align} $$
$$ \begin{align} \|\varsigma^{(\mathrm{Im}(z))}\|_{C^1} < C\sqrt{|\mathrm{Im}(z)|} \end{align} $$
for some uniform constant
![]() $C> 0$
. We consider the alternatively defined transfer operator
$C> 0$
. We consider the alternatively defined transfer operator
 $$ \begin{align*} (\hat {\mathcal L}_{z,\rho} \varphi )(u) := \smash{\sum_{\sigma(u')=u}} e^{\hat \alpha_z(u')} (\rho(\operatorname{\mathrm{Hol}}(u'))\cdot \varphi(u')), \end{align*} $$
$$ \begin{align*} (\hat {\mathcal L}_{z,\rho} \varphi )(u) := \smash{\sum_{\sigma(u')=u}} e^{\hat \alpha_z(u')} (\rho(\operatorname{\mathrm{Hol}}(u'))\cdot \varphi(u')), \end{align*} $$
where we set
 $$ \begin{align*} \hat {\alpha}_z(u) := \varsigma^{(\mathrm{Im}(z))}(u) - \mathrm{Re}(z) \cdot \tau(u,s) - \log(\varphi_{\varsigma^{(x)}}(u)) + \log(\varphi_{\varsigma^{(x)}}(\sigma(u))) - \log P(\varsigma^{(x)}) \end{align*} $$
$$ \begin{align*} \hat {\alpha}_z(u) := \varsigma^{(\mathrm{Im}(z))}(u) - \mathrm{Re}(z) \cdot \tau(u,s) - \log(\varphi_{\varsigma^{(x)}}(u)) + \log(\varphi_{\varsigma^{(x)}}(\sigma(u))) - \log P(\varsigma^{(x)}) \end{align*} $$
for
![]() $u \in U$
. By (5.31),
$u \in U$
. By (5.31),
![]() $\hat {\alpha }_z$
converges uniformly to
$\hat {\alpha }_z$
converges uniformly to
![]() $\alpha _{\mathrm {Re}(z)}$
as
$\alpha _{\mathrm {Re}(z)}$
as
![]() $\mathrm {Im}(z) \to \infty $
and, hence,
$\mathrm {Im}(z) \to \infty $
and, hence,
 $\hat {\mathcal L}_{z,\rho }\varphi $
must converge to
$\hat {\mathcal L}_{z,\rho }\varphi $
must converge to
![]() $\mathcal L_{\mathrm {Re}(z),\rho }\varphi $
in the
$\mathcal L_{\mathrm {Re}(z),\rho }\varphi $
in the
![]() $L^2(\nu ^u)$
norm.
$L^2(\nu ^u)$
norm.
Now, we simply observe that the spectral bound in Theorem 5.7 holds for the operator
 $\hat {\mathcal L}_{z,\rho }$
, because the main properties required of
$\hat {\mathcal L}_{z,\rho }$
, because the main properties required of
![]() $\hat \alpha _z$
, namely that
$\hat \alpha _z$
, namely that
![]() $\|\hat \alpha _z\|_{C^1} \leq C(1+|\mathrm {Im}(z)|)$
for large
$\|\hat \alpha _z\|_{C^1} \leq C(1+|\mathrm {Im}(z)|)$
for large
![]() $|\mathrm {Im}(z)|$
when
$|\mathrm {Im}(z)|$
when
![]() $|\mathrm {Re}(z) - P(\varsigma )| \leq 1$
, are guaranteed by (5.32) and [Reference Dolgopyat11, Lemma 1]. Moreover, note that all the constants, and particularly those originating from Proposition 5.6, can be chosen uniformly in
$|\mathrm {Re}(z) - P(\varsigma )| \leq 1$
, are guaranteed by (5.32) and [Reference Dolgopyat11, Lemma 1]. Moreover, note that all the constants, and particularly those originating from Proposition 5.6, can be chosen uniformly in
![]() $\mathrm {Im}(z)$
. As the inequality in Theorem 5.7 holds with the same constants for
$\mathrm {Im}(z)$
. As the inequality in Theorem 5.7 holds with the same constants for
 $\hat {\mathcal L}_{z,\rho }$
for each
$\hat {\mathcal L}_{z,\rho }$
for each
![]() $\mathrm {Im}(z)$
, it must hold in the limit, as desired.
$\mathrm {Im}(z)$
, it must hold in the limit, as desired.
Acknowledgements
I am indebted to my advisor, Ralf Spatzier, for his tireless and persistent support, and to Amie Wilkinson for several brief conversations that proved prescient. I am grateful to Mitul Islam for many productive exchanges, and to Clark Butler, Jon DeWitt and Mark Pollicott for pointing out errors in an earlier version of this paper. This work was supported in part by the National Science Foundation, under grant DMS 1607260.