Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-10T14:13:27.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Criteria for the density of the graph of the entropy map restricted to ergodic states

Published online by Cambridge University Press:  29 January 2016

HENRI COMMAN
HENRI COMMAN*
Affiliation:
Pontificia Universidad Católica de Valparaiso, Avenida Brasil 2950, Valparaiso, Chile email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

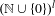We consider a non-uniquely ergodic dynamical system given by a $\mathbb{Z}^{l}$-action (or $(\mathbb{N}\cup \{0\})^{l}$-action) $\unicode[STIX]{x1D70F}$ on a non-empty compact metrisable space 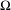$\unicode[STIX]{x1D6FA}$, for some $l\in \mathbb{N}$. Let (D) denote the following property: the graph of the restriction of the entropy map $h^{\unicode[STIX]{x1D70F}}$ to the set of ergodic states is dense in the graph of 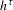$h^{\unicode[STIX]{x1D70F}}$. We assume that 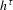$h^{\unicode[STIX]{x1D70F}}$ is finite and upper semi-continuous. We give several criteria in order that (D) holds, each of which is stated in terms of a basic notion: Gateaux differentiability of the pressure map 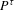$P^{\unicode[STIX]{x1D70F}}$ on some sets dense in the space $C(\unicode[STIX]{x1D6FA})$ of real-valued continuous functions on 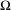$\unicode[STIX]{x1D6FA}$, level-two large deviation principle, level-one large deviation principle, convexity properties of some maps on $\mathbb{R}^{n}$ for all $n\in \mathbb{N}$. The one involving the Gateaux differentiability of $P^{\unicode[STIX]{x1D70F}}$ is of particular relevance in the context of large deviations since it establishes a clear comparison with another well-known sufficient condition: we show that for each non-empty $\unicode[STIX]{x1D70E}$-compact subset $\unicode[STIX]{x1D6F4}$ of 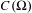$C(\unicode[STIX]{x1D6FA})$, (D) is equivalent to the existence of an infinite dimensional vector space $V$ dense in $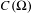C(\unicode[STIX]{x1D6FA})$ such that $f+g$ has a unique equilibrium state for all $(f,g)\in \unicode[STIX]{x1D6F4}\times V\setminus \{0\}$; any Schauder basis 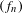$(f_{n})$ of $C(\unicode[STIX]{x1D6FA})$ whose linear span contains $\unicode[STIX]{x1D6F4}$ admits an arbitrary small perturbation $(h_{n})$ so that one can take 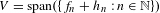$V=\text{span}(\{f_{n}+h_{n}:n\in \mathbb{N}\})$. Taking $\unicode[STIX]{x1D6F4}=\{0\}$, the existence of an infinite dimensional vector space dense in $C(\unicode[STIX]{x1D6FA})$ constituted by functions admitting a unique equilibrium state is equivalent to (D) together with the uniqueness of the measure of maximum entropy.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 3 , May 2017 , pp. 758 - 785
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beardon, A. F.. Iteration of rational functions. Complex Analytic Dynamical Systems (Graduate Texts in Mathematics, 132) . Springer, New York, 1991.Google Scholar
Comman, H.. Criteria for large deviations. Trans. Amer. Math. Soc. 355(7) (2003), 2905–2923.CrossRefGoogle Scholar
Comman, H.. Variational form of the large deviation functional. Statist. Probab. Lett. 77(9) (2007), 931–936.CrossRefGoogle Scholar
Comman, H.. Strengthened large deviations for rational maps and full shifts, with unified proof. Nonlinearity 22(6) (2009), 1413–1429.CrossRefGoogle Scholar
Comman, H. and Rivera-Letelier, J.. Large deviation principles for non-uniformly hyperbolic rational maps. Ergod. Th. & Dynam. Sys. 31(2) (2011), 321–349.CrossRefGoogle Scholar
Dembo, A. and Zeitouni, O.. Large Deviations Techniques and Applications, 2nd edn. Springer, Heidelberg, 1998.CrossRefGoogle Scholar
Ekeland, I. and Teman, R.. Convex Analysis and Variational Problems. North-Holland and American Elsevier, Amsterdam and New York, 1976.Google Scholar
Gärtner, J.. On large deviations from an invariant measure. Teor. Veroyatn. Primen. 22(1) (1977), 27–42.Google Scholar
Israel, R. B.. Generic triviality of phase diagrams in spaces of long-range interactions. Comm. Math. Phys. 106 (1986), 459–466.CrossRefGoogle Scholar
Israel, R. B. and Phelps, R. R.. Some convexity questions arising in statistical mechanics. Math. Scand. 54 (1984), 133–156.CrossRefGoogle Scholar
Kelley, J. L.. General Topology. Springer, New York, 1991.Google Scholar
Kifer, Y.. Large deviations in dynamical systems and stochastic processes. Trans. Amer. Math. Soc. 321 (1990), 505–524.CrossRefGoogle Scholar
Ljubich, M. J.. Entropy properties of rational endomorphisms of the Riemann sphere. Ergod. Th. & Dynam. Sys. 3(03) (1983), 351–385.CrossRefGoogle Scholar
Phelps, R. R.. Unique equilibrium states. Dynamics and Randomness. Eds. A. Mass et al, 2002, pp. 219–225.CrossRefGoogle Scholar
Przytycki, F., Rivera-Letelier, R. and Smirnov, S.. Equivalence and topological invariance of conditions for non-uniform hyperbolicity in the iteration of rational maps. Invent. Math. 151(1) (2003), 29–63.CrossRefGoogle Scholar
Rockafeller, R. G.. Convex Analysis. Princeton University Press, Princeton, NJ, 1970.CrossRefGoogle Scholar
Ruelle, D.. Thermodynamic Formalism. Addison-Wesley, New York, 1978.Google Scholar
Semeradi, Z.. Schauder Basis in Banach Spaces of Continuous Functions. Springer, Berlin, 1982.Google Scholar
Sokal, A. D.. More surprises in the general theory of lattice systems. Comm. Math. Phys. 86 (1982), 327–336.CrossRefGoogle Scholar