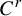1 Introduction
Following from Yoccoz [Reference Yoccoz29], the goal of the theory of dynamical systems is to understand most of the dynamics of most systems. Here ‘most systems’ means dense, generic, open and dense dynamical systems. The various perturbation techniques have played crucial roles in the study of most systems, for instance in the exploration of the famous
![]() $C^1$
-stability conjectures. Pugh’s celebrated work: the
$C^1$
-stability conjectures. Pugh’s celebrated work: the
![]() $C^1$
-closing lemma [Reference Pugh27] which realizes closing a non-wandering orbit to get periodic orbits, initiated the theory of
$C^1$
-closing lemma [Reference Pugh27] which realizes closing a non-wandering orbit to get periodic orbits, initiated the theory of
![]() $C^1$
-perturbations. Mañé’s ergodic closing lemma [Reference Mañé22] provides more information on the closing points. Another work by Mañé [Reference Mañé23] creates homoclinic points by
$C^1$
-perturbations. Mañé’s ergodic closing lemma [Reference Mañé22] provides more information on the closing points. Another work by Mañé [Reference Mañé23] creates homoclinic points by
![]() $C^r,r=1,2$
perturbations. These two works [Reference Mañé22, Reference Mañé23] are indispensable in solving the
$C^r,r=1,2$
perturbations. These two works [Reference Mañé22, Reference Mañé23] are indispensable in solving the
![]() $C^1$
-stability conjecture [Reference Mañé22, Reference Mañé24] and the ergodic closing lemma is a milestone in both differentiable dynamical systems and ergodic theory. An improved version of the
$C^1$
-stability conjecture [Reference Mañé22, Reference Mañé24] and the ergodic closing lemma is a milestone in both differentiable dynamical systems and ergodic theory. An improved version of the
![]() $C^1$
-closing lemma is obtained by Hayashi [Reference Hayashi18] that connects two orbits which visit a same small region. Hayashi’s work is now called the
$C^1$
-closing lemma is obtained by Hayashi [Reference Hayashi18] that connects two orbits which visit a same small region. Hayashi’s work is now called the
![]() $C^1$
-connecting lemma, see also works by Wen and Xia [Reference Wen and Xia28]. More developments can be found for instance in [Reference Arnaud2, Reference Gan and Wen13]. The strongest
$C^1$
-connecting lemma, see also works by Wen and Xia [Reference Wen and Xia28]. More developments can be found for instance in [Reference Arnaud2, Reference Gan and Wen13]. The strongest
![]() $C^1$
-perturbation lemma is the
$C^1$
-perturbation lemma is the
![]() $C^1$
-chain connecting lemma proved by Bonatti and Crovisier [Reference Bonatti and Crovisier4], which connects pseudo orbits under small
$C^1$
-chain connecting lemma proved by Bonatti and Crovisier [Reference Bonatti and Crovisier4], which connects pseudo orbits under small
![]() $C^1$
-perturbations. In particular, works in [Reference Bonatti and Crovisier4, Reference Crovisier8] realize closing a chain recurrent orbit (or a chain recurrent set).
$C^1$
-perturbations. In particular, works in [Reference Bonatti and Crovisier4, Reference Crovisier8] realize closing a chain recurrent orbit (or a chain recurrent set).
We recall some notions and definitions now. Let M be a
![]() $C^\infty $
closed Riemmanian manifold and denote by
$C^\infty $
closed Riemmanian manifold and denote by
![]() $\operatorname {Diff}^r(M)$
for any
$\operatorname {Diff}^r(M)$
for any
![]() $r\in \mathbb {N}\cup \{\infty \}$
the space of
$r\in \mathbb {N}\cup \{\infty \}$
the space of
![]() $C^r$
-diffeomorphisms on M endowed with the
$C^r$
-diffeomorphisms on M endowed with the
![]() $C^r$
-topology.
$C^r$
-topology.
Given
![]() $f\in \operatorname {Diff}^r(M)$
and
$f\in \operatorname {Diff}^r(M)$
and
![]() $\delta>0$
, a collection of points
$\delta>0$
, a collection of points
is called a
![]() $\delta $
-pseudo orbit if it holds
$\delta $
-pseudo orbit if it holds
Given two points
![]() $x,y\in M$
, one says that y is attainable from x under f, denoted by
$x,y\in M$
, one says that y is attainable from x under f, denoted by
![]() $x\prec _f y$
, if for any neighborhood U of x and any neighborhood V of y, there exist
$x\prec _f y$
, if for any neighborhood U of x and any neighborhood V of y, there exist
![]() $z\in U$
and
$z\in U$
and
![]() $n\geq 1$
such that
$n\geq 1$
such that
![]() $f^n(z)\in V$
; and y is chain attainable from x under f, denoted by
$f^n(z)\in V$
; and y is chain attainable from x under f, denoted by
![]() $x\dashv _f y$
, if for any
$x\dashv _f y$
, if for any
![]() $\delta>0$
, there exists a
$\delta>0$
, there exists a
![]() $\delta $
-pseudo orbit
$\delta $
-pseudo orbit
![]() $\{x_0,x_{1},\ldots ,x_n\}$
from x to y, that is,
$\{x_0,x_{1},\ldots ,x_n\}$
from x to y, that is,
![]() $x_0=x$
and
$x_0=x$
and
![]() $x_n=y$
. A point
$x_n=y$
. A point
![]() $x\in M$
is non-wandering if
$x\in M$
is non-wandering if
![]() $x\prec _f x$
, and the set of non-wandering points of f is denoted by
$x\prec _f x$
, and the set of non-wandering points of f is denoted by
![]() $\Omega (f)$
. A point
$\Omega (f)$
. A point
![]() $x\in M$
is chain recurrent if
$x\in M$
is chain recurrent if
![]() $x\dashv _f x$
, and the set of chain recurrent points of f is denoted by
$x\dashv _f x$
, and the set of chain recurrent points of f is denoted by
![]() $\operatorname {CR}(f)$
. The set of periodic points is denoted by
$\operatorname {CR}(f)$
. The set of periodic points is denoted by
![]() $\operatorname {Per}(f)$
.
$\operatorname {Per}(f)$
.
Note that compared with non-wandering/chain recurrent points, periodic points have the strongest recurrence property. One would like to ask whether or not the weaker recurrence can be perturbed into stronger ones. Given
![]() $f\in \operatorname {Diff}^r(M)$
, a point
$f\in \operatorname {Diff}^r(M)$
, a point
![]() $p\in M$
is called
$p\in M$
is called
![]() $C^r$
-closable if for any
$C^r$
-closable if for any
![]() $C^r$
-neighborhood
$C^r$
-neighborhood
![]() $\mathcal {U}$
of f, there exists
$\mathcal {U}$
of f, there exists
![]() $g\in \mathcal {U}$
such that
$g\in \mathcal {U}$
such that
![]() $p\in \operatorname {Per}(g)$
. For uniformly hyperbolic systems, Anosov’s shadowing lemma [Reference Anosov1] implies that every chain recurrent point is
$p\in \operatorname {Per}(g)$
. For uniformly hyperbolic systems, Anosov’s shadowing lemma [Reference Anosov1] implies that every chain recurrent point is
![]() $C^r$
-closable (in fact without perturbation). For a general diffeomorphism f, as has been mentioned above, Pugh’s closing lemma [Reference Pugh27] verifies that every
$C^r$
-closable (in fact without perturbation). For a general diffeomorphism f, as has been mentioned above, Pugh’s closing lemma [Reference Pugh27] verifies that every
![]() $x\in \Omega (f)$
is
$x\in \Omega (f)$
is
![]() $C^1$
-closable and Bonatti–Crovisier’s chain closing lemma [Reference Bonatti and Crovisier4] verifies every
$C^1$
-closable and Bonatti–Crovisier’s chain closing lemma [Reference Bonatti and Crovisier4] verifies every
![]() $x\in \operatorname {CR}(f)$
is
$x\in \operatorname {CR}(f)$
is
![]() $C^1$
-closable.
$C^1$
-closable.
For dynamics beyond uniform hyperbolicity and when
![]() $r\geq 2$
, things turn out to be much more complicated and delicate. Gutierrez [Reference Gutierrez15] built an example which showed that the local perturbation method for proving the
$r\geq 2$
, things turn out to be much more complicated and delicate. Gutierrez [Reference Gutierrez15] built an example which showed that the local perturbation method for proving the
![]() $C^1$
-closing lemma does not work in the
$C^1$
-closing lemma does not work in the
![]() $C^2$
-topology. Mañé [Reference Mañé23] proved a
$C^2$
-topology. Mañé [Reference Mañé23] proved a
![]() $C^2$
-connecting lemma which creates homoclinic points for hyperbolic periodic points with some assumption in the measure sense. Recently, a series progress has been achieved in the
$C^2$
-connecting lemma which creates homoclinic points for hyperbolic periodic points with some assumption in the measure sense. Recently, a series progress has been achieved in the
![]() $C^r$
-closing lemma for Hamiltonian and conservative surface diffeomorphisms, see [Reference Asaoka and Irie3, Reference Cristofaro-Gardiner, Prasad and Zhang7, Reference Edtmair and Hutchings10].
$C^r$
-closing lemma for Hamiltonian and conservative surface diffeomorphisms, see [Reference Asaoka and Irie3, Reference Cristofaro-Gardiner, Prasad and Zhang7, Reference Edtmair and Hutchings10].
In higher dimensions, Gan and the first author [Reference Gan and Shi12] proved the
![]() $C^r$
-closing lemma for partially hyperbolic diffeomorphisms with one-dimensional center bundle for every
$C^r$
-closing lemma for partially hyperbolic diffeomorphisms with one-dimensional center bundle for every
![]() $r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
. Inspired by [Reference Gan and Shi12], we explore
$r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
. Inspired by [Reference Gan and Shi12], we explore
![]() $C^r$
-perturbation results for a certain class of partially hyperbolic diffeomorphisms.
$C^r$
-perturbation results for a certain class of partially hyperbolic diffeomorphisms.
We say that a diffeomorphism
![]() $f\in \operatorname {Diff}^r(M)$
is partially hyperbolic if the tangent space
$f\in \operatorname {Diff}^r(M)$
is partially hyperbolic if the tangent space
![]() $TM$
admits a
$TM$
admits a
![]() $Df$
-invariant continuous splitting
$Df$
-invariant continuous splitting
![]() $TM=E^s\oplus E^c\oplus E^u$
and there exists
$TM=E^s\oplus E^c\oplus E^u$
and there exists
![]() $k\geq 1$
such that for any
$k\geq 1$
such that for any
![]() $x\in M$
, it holds
$x\in M$
, it holds
Here for a linear operator A, one denotes by
![]() $\|A\|$
its norm and by
$\|A\|$
its norm and by
![]() $m(A)$
its conorm, that is,
$m(A)$
its conorm, that is,
![]() $m(A)=\inf \{\|Av\|\colon \|v\|=1\}$
.
$m(A)=\inf \{\|Av\|\colon \|v\|=1\}$
.
Let
![]() $\operatorname {PH}^r(M), r\geq 1$
be the space consisting of all
$\operatorname {PH}^r(M), r\geq 1$
be the space consisting of all
![]() $C^r$
-partially hyperbolic diffeomorphisms of M endowed with the
$C^r$
-partially hyperbolic diffeomorphisms of M endowed with the
![]() $C^r$
-topology, then
$C^r$
-topology, then
![]() $\operatorname {PH}^r(M)\subset \operatorname {Diff}^r(M)$
is an open subset. We say
$\operatorname {PH}^r(M)\subset \operatorname {Diff}^r(M)$
is an open subset. We say
![]() $f\in \operatorname {PH}^r(M)$
is dynamically coherent if there exist two f-invariant foliations
$f\in \operatorname {PH}^r(M)$
is dynamically coherent if there exist two f-invariant foliations
![]() $\mathcal {F}^{cs}$
and
$\mathcal {F}^{cs}$
and
![]() $\mathcal {F}^{cu}$
that are tangent to
$\mathcal {F}^{cu}$
that are tangent to
![]() $E^s\oplus E^c$
and
$E^s\oplus E^c$
and
![]() $E^c\oplus E^u$
, respectively. It is clear that
$E^c\oplus E^u$
, respectively. It is clear that
![]() $\mathcal {F}^c=\mathcal {F}^{cs}\cap \mathcal {F}^{cu}$
is an f-invariant foliation tangent to
$\mathcal {F}^c=\mathcal {F}^{cs}\cap \mathcal {F}^{cu}$
is an f-invariant foliation tangent to
![]() $E^c$
. For a dynamically coherent partially hyperbolic diffeomorphism f, one always denotes the partially hyperbolic splitting by
$E^c$
. For a dynamically coherent partially hyperbolic diffeomorphism f, one always denotes the partially hyperbolic splitting by
![]() $TM=E_f^s\oplus E_f^c\oplus E_f^u$
or
$TM=E_f^s\oplus E_f^c\oplus E_f^u$
or
![]() $TM=E^s\oplus E^c\oplus E^u$
for simplicity when there is no confusion. Also, one denotes the stable/center/unstable foliations by
$TM=E^s\oplus E^c\oplus E^u$
for simplicity when there is no confusion. Also, one denotes the stable/center/unstable foliations by
![]() $\mathcal {F}^s/\mathcal {F}^c/\mathcal {F}^u$
.
$\mathcal {F}^s/\mathcal {F}^c/\mathcal {F}^u$
.
For
![]() $f\in \operatorname {PH}^r(M)$
being dynamically coherent and a constant
$f\in \operatorname {PH}^r(M)$
being dynamically coherent and a constant
![]() $\varepsilon>0$
, an
$\varepsilon>0$
, an
![]() $\varepsilon $
-pseudo orbit
$\varepsilon $
-pseudo orbit
![]() $\{x_i\}_{i=a}^b$
is called an
$\{x_i\}_{i=a}^b$
is called an
![]() $\varepsilon $
-center pseudo orbit if
$\varepsilon $
-center pseudo orbit if
![]() $f(x_i)\in \mathcal {F}^c_{\varepsilon }(x_{i+1})$
for any
$f(x_i)\in \mathcal {F}^c_{\varepsilon }(x_{i+1})$
for any
![]() $a\leq i\leq b-1$
. We say f is
$a\leq i\leq b-1$
. We say f is
![]() $\varepsilon $
-plaque expansive if any two bi-infinite
$\varepsilon $
-plaque expansive if any two bi-infinite
![]() $\varepsilon $
-center pseudo orbits
$\varepsilon $
-center pseudo orbits
![]() $\{x_i\}_{i\in \mathbb {Z}}, \{y_i\}_{i\in \mathbb {Z}}$
satisfying
$\{x_i\}_{i\in \mathbb {Z}}, \{y_i\}_{i\in \mathbb {Z}}$
satisfying
must satisfy
![]() $y_i\in \mathcal {F}^c_{\varepsilon }(x_i)$
for every
$y_i\in \mathcal {F}^c_{\varepsilon }(x_i)$
for every
![]() $i\in \mathbb {Z}$
. Here
$i\in \mathbb {Z}$
. Here
![]() $\mathcal {F}^c_{\varepsilon }(x)$
is the disk centered at x in
$\mathcal {F}^c_{\varepsilon }(x)$
is the disk centered at x in
![]() $\mathcal {F}^c(x)$
with radius
$\mathcal {F}^c(x)$
with radius
![]() $\varepsilon $
. We say f is plaque expansive if it is
$\varepsilon $
. We say f is plaque expansive if it is
![]() $\varepsilon $
-plaque expansive for some
$\varepsilon $
-plaque expansive for some
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Notation 1.1. For
![]() $r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
, we denote by
$r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
, we denote by
![]() $\operatorname {DPH}_1^r(M)$
(respectively
$\operatorname {DPH}_1^r(M)$
(respectively
![]() $\operatorname {DEPH}_1^r(M)$
) the set of all partially hyperbolic diffeomorphisms
$\operatorname {DEPH}_1^r(M)$
) the set of all partially hyperbolic diffeomorphisms
![]() $f\in \operatorname {PH}^r(M)$
that satisfies properties (a) and (b) (respectively (a), (b), and (c)):
$f\in \operatorname {PH}^r(M)$
that satisfies properties (a) and (b) (respectively (a), (b), and (c)):
-
(a) the center bundle
 $E^c$
is orientable with
$E^c$
is orientable with
 $\mathrm {dim}E^c=1$
, and
$\mathrm {dim}E^c=1$
, and
 $Df$
preserves the orientation;
$Df$
preserves the orientation; -
(b) f is dynamically coherent;
-
(c) f is plaque expansive.
It has been proved [Reference Hirsch, Pugh and Shub19, Theorems 7.1 and 7.4] that dynamic coherence plus plaque expansiveness is a robust property for
![]() $C^1$
-partially hyperbolic diffeomorphisms. Thus,
$C^1$
-partially hyperbolic diffeomorphisms. Thus,
![]() $\operatorname {DEPH}_1^r(M)$
forms an open set in
$\operatorname {DEPH}_1^r(M)$
forms an open set in
![]() $\operatorname {Diff}^r(M)$
for every
$\operatorname {Diff}^r(M)$
for every
![]() $r\geq 1$
. There are a series of partially hyperbolic diffeomorphisms belonging to
$r\geq 1$
. There are a series of partially hyperbolic diffeomorphisms belonging to
![]() $\operatorname {DEPH}_1^r(M)$
:
$\operatorname {DEPH}_1^r(M)$
:
-
(1) derived-from-Anosov partially hyperbolic diffeomorphisms on 3-torus
 $\mathbb {T}^3$
[Reference Hammerlindl16, Reference Potrie26], where
$\mathbb {T}^3$
[Reference Hammerlindl16, Reference Potrie26], where
 $Df$
preserves the center orientation;
$Df$
preserves the center orientation; -
(2) partially hyperbolic diffeomorphisms with circle center fibers on 3-torus
 $\mathbb {T}^3$
[Reference Hammerlindl16, Reference Potrie26] and 3-nilmanifolds N [Reference Hammerlindl and Potrie17], where
$\mathbb {T}^3$
[Reference Hammerlindl16, Reference Potrie26] and 3-nilmanifolds N [Reference Hammerlindl and Potrie17], where
 $Df$
preserves the center orientation;
$Df$
preserves the center orientation; -
(3) discretized Anosov flows [Reference Martinchich25], i.e., partially hyperbolic diffeomorphisms which are leaf conjugate to Anosov flows.
In particular, every dynamically coherent and plaque expansive partially hyperbolic diffeomorphism with one-dimensional center admits a double cover with
![]() $E^c$
orientable and an iteration of the lifting diffeomorphism belongs to
$E^c$
orientable and an iteration of the lifting diffeomorphism belongs to
![]() $\operatorname {DEPH}_1^r(M)$
.
$\operatorname {DEPH}_1^r(M)$
.
Remark 1.2. It has been conjectured [Reference Hirsch, Pugh and Shub19] that every dynamically coherent partially hyperbolic diffeomorphism must be plaque expansive. Actually, all known examples of dynamically coherent partially hyperbolic diffeomorphisms are plaque expansive.
In this paper, we prove that for every
![]() $r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
and every
$r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
and every
![]() $f\in \operatorname {DPH}_1^r(M)$
, if a point y is chain attainable from x, then any small neighborhoods of x and y can be connected through true orbits by arbitrarily small
$f\in \operatorname {DPH}_1^r(M)$
, if a point y is chain attainable from x, then any small neighborhoods of x and y can be connected through true orbits by arbitrarily small
![]() $C^r$
-perturbations of f. Let
$C^r$
-perturbations of f. Let
![]() $\mathcal {X}^r(M)$
be the space of
$\mathcal {X}^r(M)$
be the space of
![]() $C^r$
-vector fields on M for
$C^r$
-vector fields on M for
![]() $r\in \mathbb {N}\cup \{\infty \}$
. Given
$r\in \mathbb {N}\cup \{\infty \}$
. Given
![]() $X\in \mathcal {X}^r(M)$
and
$X\in \mathcal {X}^r(M)$
and
![]() $\tau \in \mathbb {R}$
, denote by
$\tau \in \mathbb {R}$
, denote by
![]() $X_\tau $
the time-
$X_\tau $
the time-
![]() $\tau $
map generated by X. We say X is transverse to a co-dimension one bundle
$\tau $
map generated by X. We say X is transverse to a co-dimension one bundle
![]() $E^s\oplus E^u$
if
$E^s\oplus E^u$
if
![]() $X(x)$
is transverse to
$X(x)$
is transverse to
![]() $E^s_x\oplus E^u_x$
in
$E^s_x\oplus E^u_x$
in
![]() $T_xM$
for every
$T_xM$
for every
![]() $x\in M$
.
$x\in M$
.
Theorem A. For any
![]() $r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
, assume
$r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
, assume
![]() $f\in \operatorname {DPH}_1^r(M)$
and
$f\in \operatorname {DPH}_1^r(M)$
and
![]() $X\in \mathcal {X}^r(M)$
is a vector field that is transverse to
$X\in \mathcal {X}^r(M)$
is a vector field that is transverse to
![]() $E^s\oplus E^u$
. For any two points
$E^s\oplus E^u$
. For any two points
![]() $x,y\in M$
with
$x,y\in M$
with
![]() $x\dashv _f y$
, there exist
$x\dashv _f y$
, there exist
![]() $p_k\in M$
,
$p_k\in M$
,
![]() $\tau _k\in \mathbb {R}$
, and
$\tau _k\in \mathbb {R}$
, and
![]() $n_k\in \mathbb {N}$
such that:
$n_k\in \mathbb {N}$
such that:
-
•
 $\tau _k\rightarrow 0$
as
$\tau _k\rightarrow 0$
as
 $k\rightarrow \infty $
;
$k\rightarrow \infty $
; -
•
 $p_k\rightarrow x$
and
$p_k\rightarrow x$
and
 $(X_{\tau _k}\circ f)^{n_k}(p_k)\rightarrow y$
as
$(X_{\tau _k}\circ f)^{n_k}(p_k)\rightarrow y$
as
 $k\rightarrow \infty $
.
$k\rightarrow \infty $
.
In particular, if
![]() $y=x$
, then
$y=x$
, then
![]() $(X_{\tau _k}\circ f)^{n_k}(p_k)=p_k$
. This means every chain recurrent point of
$(X_{\tau _k}\circ f)^{n_k}(p_k)=p_k$
. This means every chain recurrent point of
![]() $f\in \operatorname {DPH}_1^r(M)$
is
$f\in \operatorname {DPH}_1^r(M)$
is
![]() $C^r$
-closable.
$C^r$
-closable.
Remark 1.3. When
![]() $r=1$
, this orbit connecting lemma was proved by Bonatti and Crovisier in [Reference Bonatti and Crovisier4] for every
$r=1$
, this orbit connecting lemma was proved by Bonatti and Crovisier in [Reference Bonatti and Crovisier4] for every
![]() $f\in \operatorname {Diff}^1(M)$
. See [Reference Crovisier8, Reference Crovisier9] for more developments and applications of chain connecting lemmas in
$f\in \operatorname {Diff}^1(M)$
. See [Reference Crovisier8, Reference Crovisier9] for more developments and applications of chain connecting lemmas in
![]() $C^1$
-topology.
$C^1$
-topology.
Recall that
![]() $f\in \operatorname {Diff}^1(M)$
is transitive if for any two open sets
$f\in \operatorname {Diff}^1(M)$
is transitive if for any two open sets
![]() $U,V\subset M$
, there exists
$U,V\subset M$
, there exists
![]() $n\geq 1$
such that
$n\geq 1$
such that
![]() $f^n(U)\cap V\neq \emptyset $
. This is equivalent to
$f^n(U)\cap V\neq \emptyset $
. This is equivalent to
![]() $x\prec _f y$
for every
$x\prec _f y$
for every
![]() $x,y\in M$
. Similarly, f is chain transitive if
$x,y\in M$
. Similarly, f is chain transitive if
![]() $x\dashv _f y$
for every pair of points
$x\dashv _f y$
for every pair of points
![]() $x,y\in M$
. It is clear that transitivity implies chain transitivity. Concerning that
$x,y\in M$
. It is clear that transitivity implies chain transitivity. Concerning that
![]() $\operatorname {DEPH}_1^r(M)$
forms an open set in
$\operatorname {DEPH}_1^r(M)$
forms an open set in
![]() $\operatorname {Diff}^r(M)$
for every
$\operatorname {Diff}^r(M)$
for every
![]() $r\geq 1$
, we could study generic properties for
$r\geq 1$
, we could study generic properties for
![]() $\operatorname {DEPH}_1^r(M)$
. We show that for
$\operatorname {DEPH}_1^r(M)$
. We show that for
![]() $C^r$
-generic
$C^r$
-generic
![]() $f\in \operatorname {DEPH}_1^r(M)$
, transitivity and chain transitivity are equivalent. Recall that a property is generic if it holds for every element in a dense
$f\in \operatorname {DEPH}_1^r(M)$
, transitivity and chain transitivity are equivalent. Recall that a property is generic if it holds for every element in a dense
![]() $G_\delta $
subset.
$G_\delta $
subset.
Corollary B. For every
![]() $r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
, there exists a dense
$r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
, there exists a dense
![]() $G_\delta $
subset
$G_\delta $
subset
![]() $\mathcal {R}\subset \operatorname {DEPH}_1^r(M)$
such that for any
$\mathcal {R}\subset \operatorname {DEPH}_1^r(M)$
such that for any
![]() $f\in \mathcal {R}$
, the following properties hold.
$f\in \mathcal {R}$
, the following properties hold.
-
(1)
 $x\dashv _f y$
if and only if
$x\dashv _f y$
if and only if
 $x\prec _f y$
.
$x\prec _f y$
. -
(2) Periodic points are dense in the chain recurrent set:
 $\operatorname {CR}(f)=\Omega (f)=\overline {\operatorname {Per}(f)}$
.
$\operatorname {CR}(f)=\Omega (f)=\overline {\operatorname {Per}(f)}$
. -
(3) If f is chain transitive on M, then f is transitive on M.
Remark 1.4. Transitive dynamics that are beyond uniform hyperbolicity have attracted much interest from dynaminists, for instance [Reference Bonatti and Díaz5, Reference Brin6]. There exist chain transitive partially hyperbolic diffeomorphisms with one-dimensional center bundle which are accessible but not transitive [Reference Gan and Shi11]. It is worthy to see whether Corollary B holds for
![]() $C^r$
-generic partially hyperbolic diffeomorphisms with one-dimensional center bundle.
$C^r$
-generic partially hyperbolic diffeomorphisms with one-dimensional center bundle.
2 Lifting dynamics and leaf conjugacy
As have been mentioned, our proof is inspired by [Reference Gan and Shi12]. This section is devoted to state the necessary preliminaries, some of which are borrowed from [Reference Gan and Shi12]. We first give an outline.
-
• First, we give a Lipschitz center shadowing property for dynamically coherent partially hyperbolic diffeomorphisms proved in [Reference Kryzhevich and Tikhomirov21] which insures that one can always consider center pseudo orbits in our setting.
-
• Second, we parameterize each center leaf through the real line
 $\mathbb {R}$
and associate it with an order from
$\mathbb {R}$
and associate it with an order from
 $\mathbb {R}$
by the fact that
$\mathbb {R}$
by the fact that
 $\dim (E^c)=1$
. Then one could lift the center dynamics to
$\dim (E^c)=1$
. Then one could lift the center dynamics to
 $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
where each
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
where each
 $\mathbb {R}_i=\mathbb {R}$
. Moreover, we prove that by replacing some intermediate points of a center pseudo orbit if necessary, one could always assume the center pseudo orbit jumps in an ordered way. This will be done in §2.2.
$\mathbb {R}_i=\mathbb {R}$
. Moreover, we prove that by replacing some intermediate points of a center pseudo orbit if necessary, one could always assume the center pseudo orbit jumps in an ordered way. This will be done in §2.2. -
• Third, we extend the lifting dynamics on
 $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
to a tubular neighborhood by pulling back a
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
to a tubular neighborhood by pulling back a
 $C^\infty $
-bundle
$C^\infty $
-bundle
 $F^s\oplus F^u$
which is
$F^s\oplus F^u$
which is
 $C^0$
-close to
$C^0$
-close to
 $E^s\oplus E^u$
. Theorem 2.10 guarantees that the center curves for the dynamics in the tubular neighborhood admit a Lipschitz shadowing property under perturbations. This appears in §§2.3 and 2.4.
$E^s\oplus E^u$
. Theorem 2.10 guarantees that the center curves for the dynamics in the tubular neighborhood admit a Lipschitz shadowing property under perturbations. This appears in §§2.3 and 2.4. -
• Finally, based on the preparations in this section, we will prove a push-forward (or push-backward) perturbation result in §3 which allows us to prove Theorem A by more delicate estimates.
One first recalls the following proposition from [Reference Kryzhevich and Tikhomirov21, Theorem 1] which states a Lipschitz center shadowing property for dynamically coherent partially hyperbolic diffeomorphisms. Roughly speaking, for such a system, any pseudo orbit with small jumps would be shadowed by a center pseudo orbit. See also similar results in [Reference Hu, Zhou and Zhu20].
Proposition 2.1. [Reference Kryzhevich and Tikhomirov21]
Assume
![]() $f\in \operatorname {PH}^1(M)$
is dynamically coherent. Then there exist
$f\in \operatorname {PH}^1(M)$
is dynamically coherent. Then there exist
![]() $\varepsilon _0>0$
and
$\varepsilon _0>0$
and
![]() $L>1$
such that for any
$L>1$
such that for any
![]() $\varepsilon \in (0,\varepsilon _0)$
and any
$\varepsilon \in (0,\varepsilon _0)$
and any
![]() $\varepsilon $
-pseudo orbit
$\varepsilon $
-pseudo orbit
![]() $\{w_a,w_{a+1},\ldots ,w_b\}, -\infty \leq a<b\leq +\infty $
, there exists an
$\{w_a,w_{a+1},\ldots ,w_b\}, -\infty \leq a<b\leq +\infty $
, there exists an
![]() $L\varepsilon $
-center pseudo orbit
$L\varepsilon $
-center pseudo orbit
![]() $\{x_a,x_{a+1},\ldots ,x_b\}$
satisfying
$\{x_a,x_{a+1},\ldots ,x_b\}$
satisfying
Moreover, if
![]() $w_a=w_b$
where
$w_a=w_b$
where
![]() $-\infty <a<b<+\infty $
, then the new center pseudo orbit can be chosen to satisfy
$-\infty <a<b<+\infty $
, then the new center pseudo orbit can be chosen to satisfy
![]() $x_a=x_b$
.
$x_a=x_b$
.
Proof of the ‘moreover’ part
The statement of Proposition 2.1 before the ‘moreover’ part is [Reference Kryzhevich and Tikhomirov21, Theorem 1]. Thus, we only need to prove the ‘moreover’ part. We first revisit the steps in the proof of [Reference Kryzhevich and Tikhomirov21, Theorem 1]. Note that one could always consider a bi-infinite pseudo orbit
![]() $\{w_i\}_{i\in \mathbb {Z}}$
because any finite or one-sided-infinite pseudo orbit can be extended naturally to a bi-infinite one (see for instance §2.2 below).
$\{w_i\}_{i\in \mathbb {Z}}$
because any finite or one-sided-infinite pseudo orbit can be extended naturally to a bi-infinite one (see for instance §2.2 below).
(1) Fix two constants
![]() $\delta _0>0, L_0>1$
such that for any
$\delta _0>0, L_0>1$
such that for any
![]() $0<\delta \le \delta _0$
and any two points
$0<\delta \le \delta _0$
and any two points
![]() $x,y\in M$
satisfying
$x,y\in M$
satisfying
![]() $d(x,y)<\delta $
, then
$d(x,y)<\delta $
, then
![]() $\mathcal {F}_x^{cu}(L_0\delta )$
intersects
$\mathcal {F}_x^{cu}(L_0\delta )$
intersects
![]() $\mathcal {F}_y^s(L_0\delta )$
at a unique point and similarly for
$\mathcal {F}_y^s(L_0\delta )$
at a unique point and similarly for
![]() $\mathcal {F}_x^{cs}(L_0\delta )$
and
$\mathcal {F}_x^{cs}(L_0\delta )$
and
![]() $\mathcal {F}_y^u(L_0\delta )$
. This local product property is guaranteed by the transversality and continuation of local foliations.
$\mathcal {F}_y^u(L_0\delta )$
. This local product property is guaranteed by the transversality and continuation of local foliations.
(2) By considering an iterate of f [Reference Kryzhevich and Tikhomirov21, Lemma 1] (or by taking an adapted metric as in §2) and by decreasing
![]() $\delta _0$
if necessary, one has
$\delta _0$
if necessary, one has
where
![]() $d^{s/u}$
denotes the metric on the stable/unstable foliations and
$d^{s/u}$
denotes the metric on the stable/unstable foliations and
![]() $\unicode{x3bb} \in (0,1)$
is a constant depending only on the contracting/expanding ratio of
$\unicode{x3bb} \in (0,1)$
is a constant depending only on the contracting/expanding ratio of
![]() $Df$
along
$Df$
along
![]() $E^s/E^u$
.
$E^s/E^u$
.
(3) Then there exist two constants
![]() $\varepsilon _0\in (0,\delta _0)$
and
$\varepsilon _0\in (0,\delta _0)$
and
![]() $L_1>L_0$
such that for any
$L_1>L_0$
such that for any
![]() $\varepsilon \in (0,\varepsilon _0)$
and any bi-infinite
$\varepsilon \in (0,\varepsilon _0)$
and any bi-infinite
![]() $\varepsilon $
-pseudo orbit
$\varepsilon $
-pseudo orbit
![]() $\{w_i\}_{i\in \mathbb {Z}}$
, the map
$\{w_i\}_{i\in \mathbb {Z}}$
, the map
![]() $h_i^s\colon \mathcal {F}^s_{w_i}(L_1\varepsilon )\rightarrow \mathcal {F}^s_{w_{i+1}}(L_1\varepsilon )$
is well defined where for every
$h_i^s\colon \mathcal {F}^s_{w_i}(L_1\varepsilon )\rightarrow \mathcal {F}^s_{w_{i+1}}(L_1\varepsilon )$
is well defined where for every
![]() $z\in \mathcal {F}^s_{w_i}(L_1\varepsilon )$
, the image
$z\in \mathcal {F}^s_{w_i}(L_1\varepsilon )$
, the image
![]() $h_i^s(z)$
is the unique point of
$h_i^s(z)$
is the unique point of
![]() $\mathcal {F}^{cu}_{f(z)}(L_0\delta _0)\cap \mathcal {F}^s_{w_{i+1}}(L_1\varepsilon )$
. This corresponds to [Reference Kryzhevich and Tikhomirov21, Lemma 2].
$\mathcal {F}^{cu}_{f(z)}(L_0\delta _0)\cap \mathcal {F}^s_{w_{i+1}}(L_1\varepsilon )$
. This corresponds to [Reference Kryzhevich and Tikhomirov21, Lemma 2].
(4) Consider the set
![]() $X^s=\prod _{i=-\infty }^{+\infty }\mathcal {F}^s_{w_i}(L_1\varepsilon )$
endowed with the Tikhonov product topology and consider the map
$X^s=\prod _{i=-\infty }^{+\infty }\mathcal {F}^s_{w_i}(L_1\varepsilon )$
endowed with the Tikhonov product topology and consider the map
![]() $H\colon X^s\rightarrow X^s$
with (a bit different to [Reference Kryzhevich and Tikhomirov21] as they are working on the tangent bundle while here we consider local leaves on the manifold directly. These two ways are equivalent through the exponential map)
$H\colon X^s\rightarrow X^s$
with (a bit different to [Reference Kryzhevich and Tikhomirov21] as they are working on the tangent bundle while here we consider local leaves on the manifold directly. These two ways are equivalent through the exponential map)
Applying the Tikhonov–Schauder fixed point theorem, the map H has a (maybe not unique) fixed point. This induces an orbit of center unstable leaves
![]() $\{\mathcal {F}^{cu}_{y^s_i}\}_{i\in \mathbb {Z}}$
(that is,
$\{\mathcal {F}^{cu}_{y^s_i}\}_{i\in \mathbb {Z}}$
(that is,
![]() $f(\mathcal {F}^{cu}_{y^s_i})=\mathcal {F}^{cu}_{y^s_{i+1}}$
for any
$f(\mathcal {F}^{cu}_{y^s_i})=\mathcal {F}^{cu}_{y^s_{i+1}}$
for any
![]() $i\in \mathbb {Z}$
) where
$i\in \mathbb {Z}$
) where
![]() $y^s_{i+1}\in \mathcal {F}^{cu}_{f(y^s_i)}(L_1\varepsilon )$
and which satisfies that
$y^s_{i+1}\in \mathcal {F}^{cu}_{f(y^s_i)}(L_1\varepsilon )$
and which satisfies that
![]() $y^s_{i}$
is close to
$y^s_{i}$
is close to
![]() $w_i\text { for all } i\in \mathbb {Z}$
. Symmetrically, one obtains an orbit of center stable leaves
$w_i\text { for all } i\in \mathbb {Z}$
. Symmetrically, one obtains an orbit of center stable leaves
![]() $\{\mathcal {F}^{cs}_{y^u_i}\}_{i\in \mathbb {Z}}$
which satisfies that
$\{\mathcal {F}^{cs}_{y^u_i}\}_{i\in \mathbb {Z}}$
which satisfies that
![]() $y^u_{i}$
is close to
$y^u_{i}$
is close to
![]() $w_i\text { for all } i\in \mathbb {Z}$
.
$w_i\text { for all } i\in \mathbb {Z}$
.
(5) The intersection
![]() $\{\mathcal {F}^{cs}_{y^u_i}\cap \mathcal {F}^{cu}_{y^s_i}\}_{i\in \mathbb {Z}}$
forms an orbit of center leaves
$\{\mathcal {F}^{cs}_{y^u_i}\cap \mathcal {F}^{cu}_{y^s_i}\}_{i\in \mathbb {Z}}$
forms an orbit of center leaves
![]() $\{\mathcal {F}^{c}_{y_i}\}_{i\in \mathbb {Z}}$
with
$\{\mathcal {F}^{c}_{y_i}\}_{i\in \mathbb {Z}}$
with
![]() $y_i$
being close to
$y_i$
being close to
![]() $w_i$
for all
$w_i$
for all
![]() $i\in \mathbb {Z}$
. Finally, following arguments in [Reference Kryzhevich and Tikhomirov21, pp. 2907–2908], there exists a center pseudo orbit
$i\in \mathbb {Z}$
. Finally, following arguments in [Reference Kryzhevich and Tikhomirov21, pp. 2907–2908], there exists a center pseudo orbit
![]() $\{x_i\}_{i\in \mathbb {Z}}$
that shadows
$\{x_i\}_{i\in \mathbb {Z}}$
that shadows
![]() $\{w_i\}_{i\in \mathbb {Z}}$
. In this step, the constant
$\{w_i\}_{i\in \mathbb {Z}}$
. In this step, the constant
![]() $\varepsilon _0$
may be decreasing once again and
$\varepsilon _0$
may be decreasing once again and
![]() $L_1$
is replaced by a larger L.
$L_1$
is replaced by a larger L.
The ‘moreover’ part is almost included in the proof of [Reference Kryzhevich and Tikhomirov21, Theorem 1]. We give an explanation here. To simplify symbols, we let
![]() $0=a<b=n<+\infty $
and consider a pseudo orbit
$0=a<b=n<+\infty $
and consider a pseudo orbit
![]() $\{w_0,w_{1},\ldots ,w_n\}$
with
$\{w_0,w_{1},\ldots ,w_n\}$
with
![]() $w_n=w_0$
. One first repeats it forward and backward to get a bi-infinite periodic pseudo orbit, that is, let
$w_n=w_0$
. One first repeats it forward and backward to get a bi-infinite periodic pseudo orbit, that is, let
![]() $w_i=w_{i~\mathrm {mod}~n}$
for
$w_i=w_{i~\mathrm {mod}~n}$
for
![]() $i\in \mathbb {Z}$
. Then Steps (1)–(3) still work. We only need to verify that in Step (4), one could choose a fixed point of H which induces a periodic orbit of center unstable leaves
$i\in \mathbb {Z}$
. Then Steps (1)–(3) still work. We only need to verify that in Step (4), one could choose a fixed point of H which induces a periodic orbit of center unstable leaves
![]() $\{\mathcal {F}^{cu}_{y^s_i}\}_{i\in \mathbb {Z}}$
, that is,
$\{\mathcal {F}^{cu}_{y^s_i}\}_{i\in \mathbb {Z}}$
, that is,
![]() $y^s_i=y^s_{i~\mathrm {mod}~n}$
. To do this, we consider the finite composition (rather than considering H)
$y^s_i=y^s_{i~\mathrm {mod}~n}$
. To do this, we consider the finite composition (rather than considering H)
which is well defined by Step (3). Note that each
![]() $h^s_i$
is a composition of a local
$h^s_i$
is a composition of a local
![]() $cu$
-holonomy with f, thus,
$cu$
-holonomy with f, thus,
![]() $H^s_n$
is continuous. However,
$H^s_n$
is continuous. However,
![]() $H^s_n$
maps
$H^s_n$
maps
![]() $\mathcal {F}^s_{w_0}(L_1\varepsilon )$
into itself where
$\mathcal {F}^s_{w_0}(L_1\varepsilon )$
into itself where
![]() $\mathcal {F}^s_{w_0}(L_1\varepsilon )$
is an s-dimensional disk. Applying the Tikhonov–Schauder fixed point theorem, the map
$\mathcal {F}^s_{w_0}(L_1\varepsilon )$
is an s-dimensional disk. Applying the Tikhonov–Schauder fixed point theorem, the map
![]() $H^s_n$
has a (maybe not unique) fixed point
$H^s_n$
has a (maybe not unique) fixed point
![]() $y^s_0\in \mathcal {F}^s_{w_0}(L_1\varepsilon )$
. This induces an orbit segment of center unstable leaves
$y^s_0\in \mathcal {F}^s_{w_0}(L_1\varepsilon )$
. This induces an orbit segment of center unstable leaves
![]() $\{\mathcal {F}^{cu}_{y^s_i}\}_{i\in [0,n]}$
with
$\{\mathcal {F}^{cu}_{y^s_i}\}_{i\in [0,n]}$
with
![]() $f(\mathcal {F}^{cu}_{y^s_i})=\mathcal {F}^{cu}_{y^s_{i+1}}$
for
$f(\mathcal {F}^{cu}_{y^s_i})=\mathcal {F}^{cu}_{y^s_{i+1}}$
for
![]() $0\leq i\leq n-1$
and
$0\leq i\leq n-1$
and
![]() $y^s_0=y^s_n$
. Moreover, one also has that
$y^s_0=y^s_n$
. Moreover, one also has that
![]() $y^s_{i}$
is close to
$y^s_{i}$
is close to
![]() $w_i\text { for all } i\in [0,n]$
following arguments in [Reference Kryzhevich and Tikhomirov21, pp. 2907–2908]. Repeating
$w_i\text { for all } i\in [0,n]$
following arguments in [Reference Kryzhevich and Tikhomirov21, pp. 2907–2908]. Repeating
![]() $\{\mathcal {F}^{cu}_{y^s_i}\}_{i\in [0,n]}$
forward and backward, that is, let
$\{\mathcal {F}^{cu}_{y^s_i}\}_{i\in [0,n]}$
forward and backward, that is, let
![]() $y^s_i=y^s_{i~\mathrm {mod}~n}$
for
$y^s_i=y^s_{i~\mathrm {mod}~n}$
for
![]() $i\in \mathbb {Z}$
, one gets a periodic orbit of center unstable leaves
$i\in \mathbb {Z}$
, one gets a periodic orbit of center unstable leaves
![]() $\{\mathcal {F}^{cu}_{y^s_i}\}_{i\in \mathbb {Z}}$
. Symmetrically, we can get a periodic orbit of center stable leaves
$\{\mathcal {F}^{cu}_{y^s_i}\}_{i\in \mathbb {Z}}$
. Symmetrically, we can get a periodic orbit of center stable leaves
![]() $\{\mathcal {F}^{cs}_{y^u_i}\}_{i\in \mathbb {Z}}$
. As in Step (5), the intersection
$\{\mathcal {F}^{cs}_{y^u_i}\}_{i\in \mathbb {Z}}$
. As in Step (5), the intersection
![]() $\{\mathcal {F}^{cs}_{y^u_i}\cap \mathcal {F}^{cu}_{y^s_i}\}_{i\in \mathbb {Z}}$
forms a periodic orbit of center leaves
$\{\mathcal {F}^{cs}_{y^u_i}\cap \mathcal {F}^{cu}_{y^s_i}\}_{i\in \mathbb {Z}}$
forms a periodic orbit of center leaves
![]() $\{\mathcal {F}^{c}_{y_i}\}_{i\in \mathbb {Z}}$
with
$\{\mathcal {F}^{c}_{y_i}\}_{i\in \mathbb {Z}}$
with
![]() $y_i$
being close to
$y_i$
being close to
![]() $w_i$
for all
$w_i$
for all
![]() $i\in [0,n]$
and
$i\in [0,n]$
and
![]() $y_i=y_{i~\mathrm {mod}~n}$
. We take
$y_i=y_{i~\mathrm {mod}~n}$
. We take
![]() $x_i$
to be the unique intersection of the local leaf of
$x_i$
to be the unique intersection of the local leaf of
![]() $\mathcal {F}^{cu}_{y^s_i}$
with the local leaf of
$\mathcal {F}^{cu}_{y^s_i}$
with the local leaf of
![]() $\mathcal {F}^{s}_{y^u_i}$
. Here,
$\mathcal {F}^{s}_{y^u_i}$
. Here,
![]() $\{x_i\}_{i=0}^n$
is the periodic
$\{x_i\}_{i=0}^n$
is the periodic
![]() $L\epsilon $
-center pseudo orbit we need, see [Reference Kryzhevich and Tikhomirov21, p. 2908] for the estimation of the constant L. (This is the first line of [Reference Kryzhevich and Tikhomirov21, p. 2908] where they use the notation ‘
$L\epsilon $
-center pseudo orbit we need, see [Reference Kryzhevich and Tikhomirov21, p. 2908] for the estimation of the constant L. (This is the first line of [Reference Kryzhevich and Tikhomirov21, p. 2908] where they use the notation ‘
![]() $y_k$
’ while here we use ‘
$y_k$
’ while here we use ‘
![]() $x_i$
’.)
$x_i$
’.)
Remark 2.2. As a consequence of Proposition 2.1, for a dynamically coherent
![]() $f\in \operatorname {PH}^1(M)$
, for any
$f\in \operatorname {PH}^1(M)$
, for any
![]() $x\in \operatorname {CR}(f)$
and any
$x\in \operatorname {CR}(f)$
and any
![]() $\varepsilon>0$
, there exists a periodic
$\varepsilon>0$
, there exists a periodic
![]() $\varepsilon $
-center pseudo orbit
$\varepsilon $
-center pseudo orbit
2.1 Preliminary settings
From now on, unless emphasized, we always assume
![]() $f\in \operatorname {DPH}_1^r(M), r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
. In this subsection, we will fix some elements for
$f\in \operatorname {DPH}_1^r(M), r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
. In this subsection, we will fix some elements for
![]() $f\in \operatorname {DPH}_1^r(M), r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
. The first is a metric on M that is adapted to the partially hyperbolic splitting. Second, one associates an order to each (
$f\in \operatorname {DPH}_1^r(M), r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
. The first is a metric on M that is adapted to the partially hyperbolic splitting. Second, one associates an order to each (
![]() $1$
-dimensional) center bundle. Finally, one fixes two
$1$
-dimensional) center bundle. Finally, one fixes two
![]() $C^\infty $
-sub-bundles
$C^\infty $
-sub-bundles
![]() $F^s$
and
$F^s$
and
![]() $F^u$
that are
$F^u$
that are
![]() $C^0$
-close to
$C^0$
-close to
![]() $E^s$
and
$E^s$
and
![]() $E^u$
, respectively.
$E^u$
, respectively.
Let d be a
![]() $C^{\infty }$
-Riemannian metric on M that is adapted [Reference Gourmelon14] to the splitting
$C^{\infty }$
-Riemannian metric on M that is adapted [Reference Gourmelon14] to the splitting
![]() $E^s\oplus E^c\oplus E^u$
. To be precise, there exist constants
$E^s\oplus E^c\oplus E^u$
. To be precise, there exist constants
![]() $0<\unicode{x3bb} <1$
and
$0<\unicode{x3bb} <1$
and
![]() $0<\eta _0<10^{-3}$
such that for any
$0<\eta _0<10^{-3}$
such that for any
![]() $z\in M$
, it satisfies:
$z\in M$
, it satisfies:
-
•
 $\|Df|_{E^s_z}\|<\min \{\unicode{x3bb} ,\|Df|_{E^c_z}\|\}\leq \max \{\unicode{x3bb} ^{-1},\|Df|_{E^c_z}\|\}<m(Df|_{E^u_z})$
;
$\|Df|_{E^s_z}\|<\min \{\unicode{x3bb} ,\|Df|_{E^c_z}\|\}\leq \max \{\unicode{x3bb} ^{-1},\|Df|_{E^c_z}\|\}<m(Df|_{E^u_z})$
; -
• the three sub-bundles are almost orthogonal mutually:
 $$ \begin{align*}\min\limits_{v^{\alpha}\in E^{\alpha}_z,\|v^{\alpha}\|=1} d_{T_zM}(v^{\alpha},E^{\beta}_z\oplus E^{\gamma}_z)>1-\eta_0 \quad\text{where } \{\alpha,\beta,\gamma\}=\{s,c,u\};\end{align*} $$
$$ \begin{align*}\min\limits_{v^{\alpha}\in E^{\alpha}_z,\|v^{\alpha}\|=1} d_{T_zM}(v^{\alpha},E^{\beta}_z\oplus E^{\gamma}_z)>1-\eta_0 \quad\text{where } \{\alpha,\beta,\gamma\}=\{s,c,u\};\end{align*} $$
-
• for
 $\alpha =s,c,u$
, the projection
$\alpha =s,c,u$
, the projection
 $\pi _z^{\alpha }\colon T_zM\rightarrow E^{\alpha }_z$
satisfies
$\pi _z^{\alpha }\colon T_zM\rightarrow E^{\alpha }_z$
satisfies
 $\|\pi _z^{\alpha }(v)\|\leq 2\|v\|$
for any
$\|\pi _z^{\alpha }(v)\|\leq 2\|v\|$
for any
 $v\in T_zM$
.
$v\in T_zM$
.
Here,
![]() $\|\cdot \|$
is the vector norm on
$\|\cdot \|$
is the vector norm on
![]() $TM$
and
$TM$
and
![]() $d_{T_zM}(\cdot ,\cdot )$
is the distance induced by the Riemannian metric d. Such an adapted Riemmanian metric d always exists by the classical arguments in [Reference Hirsch, Pugh and Shub19].
$d_{T_zM}(\cdot ,\cdot )$
is the distance induced by the Riemannian metric d. Such an adapted Riemmanian metric d always exists by the classical arguments in [Reference Hirsch, Pugh and Shub19].
Denote by
![]() $\pi \colon TM\rightarrow M$
the natural projection from
$\pi \colon TM\rightarrow M$
the natural projection from
![]() $TM$
to M and by
$TM$
to M and by
![]() ${\pi ^\alpha \colon TM\rightarrow E^\alpha }$
the bundle projection map. For
${\pi ^\alpha \colon TM\rightarrow E^\alpha }$
the bundle projection map. For
![]() $v\in TM$
, let
$v\in TM$
, let
![]() $v=v^s+v^c+v^u$
be the direct sum splitting with
$v=v^s+v^c+v^u$
be the direct sum splitting with
![]() $v^\alpha =\pi ^\alpha (v)$
,
$v^\alpha =\pi ^\alpha (v)$
,
![]() $\alpha =s,c,u$
. To simplify notation, denote
$\alpha =s,c,u$
. To simplify notation, denote
![]() $s=\dim (E^s)$
and
$s=\dim (E^s)$
and
![]() ${u=\dim (E^u)}$
. For any constant
${u=\dim (E^u)}$
. For any constant
![]() $a>0$
, the a-cone field
$a>0$
, the a-cone field
![]() $\mathcal {C}_a(E^c)$
of
$\mathcal {C}_a(E^c)$
of
![]() $E^c$
is defined as
$E^c$
is defined as
A
![]() $C^1$
-curve
$C^1$
-curve
![]() $\gamma \colon I\rightarrow M$
, where I is an interval, is called tangent to the a-cone field of
$\gamma \colon I\rightarrow M$
, where I is an interval, is called tangent to the a-cone field of
![]() $E^c$
if the tangent line of
$E^c$
if the tangent line of
![]() $\gamma $
is contained in
$\gamma $
is contained in
![]() $\mathcal {C}_a(E^c)$
everywhere.
$\mathcal {C}_a(E^c)$
everywhere.
Let
![]() $X\in \mathcal {X}^r(M)$
be a vector field that is transverse to
$X\in \mathcal {X}^r(M)$
be a vector field that is transverse to
![]() $E^s\oplus E^u$
everywhere. Since
$E^s\oplus E^u$
everywhere. Since
![]() $\dim (E^c)=1$
, one has that
$\dim (E^c)=1$
, one has that
![]() $E^c_z\cong \mathbb {R}$
for any
$E^c_z\cong \mathbb {R}$
for any
![]() $z\in M$
. Moreover, since
$z\in M$
. Moreover, since
![]() $E^c$
is orientable and
$E^c$
is orientable and
![]() $Df$
preserves the orientation, one can associate to each
$Df$
preserves the orientation, one can associate to each
![]() $E^c_z$
an order induced by
$E^c_z$
an order induced by
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
![]() $Df|_{E^c}$
keeps this order. Without loss of generality, we assume that
$Df|_{E^c}$
keeps this order. Without loss of generality, we assume that
![]() $X\in \mathcal {X}^r(M)$
is positively transverse to
$X\in \mathcal {X}^r(M)$
is positively transverse to
![]() $E^s\oplus E^u$
everywhere. To be precise, it satisfies that
$E^s\oplus E^u$
everywhere. To be precise, it satisfies that
![]() $\pi ^c(X(z))>0$
with respect to the order of
$\pi ^c(X(z))>0$
with respect to the order of
![]() $E^c_z$
for every
$E^c_z$
for every
![]() $z\in M$
. The other case when X is negatively transverse to
$z\in M$
. The other case when X is negatively transverse to
![]() $E^s\oplus E^u$
everywhere is symmetric by taking the inverse orientation of
$E^s\oplus E^u$
everywhere is symmetric by taking the inverse orientation of
![]() $E^c$
.
$E^c$
.
Note that in general,
![]() $E^s$
and
$E^s$
and
![]() $E^u$
are only continuous sub-bundles of
$E^u$
are only continuous sub-bundles of
![]() $TM$
. One takes two
$TM$
. One takes two
![]() $C^\infty $
-sub-bundles
$C^\infty $
-sub-bundles
![]() $F^s$
and
$F^s$
and
![]() $F^u$
of
$F^u$
of
![]() $TM$
that are
$TM$
that are
![]() $\eta _0$
-
$\eta _0$
-
![]() $C^0$
-close to
$C^0$
-close to
![]() $E^s$
and
$E^s$
and
![]() $E^u$
, respectively. To be precise,
$E^u$
, respectively. To be precise,
 $$ \begin{align*}\dim(F^\alpha)&=\dim(E^\alpha) \quad\text{and}\quad \angle(F^\alpha,E^\alpha)\\&=\max\limits_{z\in M}\max\limits_{v\in F^\alpha_z,\|v\|=1}d_{T_zM}(v,E^\alpha_z)<\eta_0 \quad\text{for } \alpha=s,u.\end{align*} $$
$$ \begin{align*}\dim(F^\alpha)&=\dim(E^\alpha) \quad\text{and}\quad \angle(F^\alpha,E^\alpha)\\&=\max\limits_{z\in M}\max\limits_{v\in F^\alpha_z,\|v\|=1}d_{T_zM}(v,E^\alpha_z)<\eta_0 \quad\text{for } \alpha=s,u.\end{align*} $$
Thus,
![]() $TM=F^s\oplus E^c\oplus F^u$
is still a direct sum decomposition. In particular, by taking
$TM=F^s\oplus E^c\oplus F^u$
is still a direct sum decomposition. In particular, by taking
![]() $F^s$
and
$F^s$
and
![]() $F^u$
close enough to
$F^u$
close enough to
![]() $E^s$
and
$E^s$
and
![]() $E^u$
, respectively, one can guarantee that X is also transverse to
$E^u$
, respectively, one can guarantee that X is also transverse to
![]() $F^s\oplus F^u$
.
$F^s\oplus F^u$
.
2.2 Parameterizing and lifting center dynamics
For each
![]() $z\in M$
, denote by
$z\in M$
, denote by
![]() $\mathcal {F}^c_z$
the center leaf of z. Based on the fact that
$\mathcal {F}^c_z$
the center leaf of z. Based on the fact that
![]() $\dim (\mathcal {F}^c_z)=1$
, one parameterizes the center leaves
$\dim (\mathcal {F}^c_z)=1$
, one parameterizes the center leaves
![]() $\{\mathcal {F}^c_z\}_{z\in M}$
and lifts the center dynamics on the parameterization. Then we prove that every center pseudo orbit with small jumps could be replaced by one that jumps in an ordered way and that preserves the initial and end points, see Lemma 2.5.
$\{\mathcal {F}^c_z\}_{z\in M}$
and lifts the center dynamics on the parameterization. Then we prove that every center pseudo orbit with small jumps could be replaced by one that jumps in an ordered way and that preserves the initial and end points, see Lemma 2.5.
2.2.1 Parameterization of the center foliation
Note that
![]() $\mathcal {F}^c_z$
either is non-compact and diffeomorphic to
$\mathcal {F}^c_z$
either is non-compact and diffeomorphic to
![]() $\mathbb {R}$
, or is compact and diffeomorphic to
$\mathbb {R}$
, or is compact and diffeomorphic to
![]() $\mathbb {S}^1$
. Let
$\mathbb {S}^1$
. Let
![]() $\theta _z\colon \mathbb {R}\rightarrow \mathcal {F}^c_z$
be a
$\theta _z\colon \mathbb {R}\rightarrow \mathcal {F}^c_z$
be a
![]() $C^1$
map such that:
$C^1$
map such that:
-
•
 $\theta _z(0)=z$
;
$\theta _z(0)=z$
; -
•
 $\theta _z'(t)$
is the positive unit vector of
$\theta _z'(t)$
is the positive unit vector of
 $E^c_{\theta _z(t)}$
for all
$E^c_{\theta _z(t)}$
for all
 $t\in \mathbb {R}$
.
$t\in \mathbb {R}$
.
To emphasize the dependence of the base point z, we denote
![]() $\mathbb {R}_z=\theta _z^{-1}(\mathcal {F}^c_z)$
. Note that when
$\mathbb {R}_z=\theta _z^{-1}(\mathcal {F}^c_z)$
. Note that when
![]() $\mathcal {F}^c_z$
is non-compact, then
$\mathcal {F}^c_z$
is non-compact, then
![]() $\theta _z$
is a diffeomorphism and is isometric in the sense that
$\theta _z$
is a diffeomorphism and is isometric in the sense that
![]() $d^c(\theta _z(t_1),\theta _z(t_2))=|t_2-t_1|$
, where
$d^c(\theta _z(t_1),\theta _z(t_2))=|t_2-t_1|$
, where
![]() $d^c(\cdot ,\cdot )$
is the metric on the center foliations. When
$d^c(\cdot ,\cdot )$
is the metric on the center foliations. When
![]() $\mathcal {F}^c_z$
is compact, then
$\mathcal {F}^c_z$
is compact, then
![]() $\theta _z$
is a universal covering map and is locally isometric.
$\theta _z$
is a universal covering map and is locally isometric.
2.2.2 The constant
 $\varepsilon _0$
$\varepsilon _0$
Since the length of all (compact) center leaves has a uniform lower bound, one can take a small constant
![]() $0<\varepsilon _0<1$
such that for every
$0<\varepsilon _0<1$
such that for every
![]() $z\in M$
and every interval I with length no larger than
$z\in M$
and every interval I with length no larger than
![]() $10\varepsilon _0$
, the restricted map
$10\varepsilon _0$
, the restricted map
![]() $\theta _z|_{I}$
is isometric.
$\theta _z|_{I}$
is isometric.
Take
![]() $\varepsilon \in (0,\varepsilon _0)$
. Assume
$\varepsilon \in (0,\varepsilon _0)$
. Assume
is an
![]() $\varepsilon $
-center pseudo orbit. One extends
$\varepsilon $
-center pseudo orbit. One extends
![]() $\Gamma $
to be bi-infinite. To be precise, let
$\Gamma $
to be bi-infinite. To be precise, let
such that
To simplify notation, denote
![]() $\mathbb {R}_{i}=\mathbb {R}_{x_i}$
and
$\mathbb {R}_{i}=\mathbb {R}_{x_i}$
and
![]() $\theta _i=\theta _{x_i}\colon \mathbb {R}_{i}\rightarrow \mathcal {F}^c_{x_i}$
. Since
$\theta _i=\theta _{x_i}\colon \mathbb {R}_{i}\rightarrow \mathcal {F}^c_{x_i}$
. Since
![]() $f(x_i)\in \mathcal {F}^c_{x_{i+1}}$
and each
$f(x_i)\in \mathcal {F}^c_{x_{i+1}}$
and each
![]() $\theta _i$
is locally isometric, then there exists a unique
$\theta _i$
is locally isometric, then there exists a unique
![]() $t_{i+1}\in (-\varepsilon ,\varepsilon )$
such that
$t_{i+1}\in (-\varepsilon ,\varepsilon )$
such that
![]() $f(x_i)=\theta _{i+1}(t_{i+1})$
. In particular, one has
$f(x_i)=\theta _{i+1}(t_{i+1})$
. In particular, one has
![]() $t_{i+1}=0$
when
$t_{i+1}=0$
when
![]() $i\leq -1$
or
$i\leq -1$
or
![]() $i\geq n$
.
$i\geq n$
.
2.2.3 Lifting dynamics
Note that
![]() $\{\theta _z\}_{z\in M}$
defines a line-fiber over M. The dynamical system
$\{\theta _z\}_{z\in M}$
defines a line-fiber over M. The dynamical system
![]() $f\colon M\rightarrow M$
induces natural dynamics
$f\colon M\rightarrow M$
induces natural dynamics
![]() $ \widehat {f}\colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
such that
$ \widehat {f}\colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
such that
![]() $\text { for all } i\in \mathbb {Z}$
, the restriction
$\text { for all } i\in \mathbb {Z}$
, the restriction
![]() $\widehat {f}|_{\mathbb {R}_i}\colon \mathbb {R}_i\rightarrow \mathbb {R}_{i+1}$
is a diffeomorphism and
$\widehat {f}|_{\mathbb {R}_i}\colon \mathbb {R}_i\rightarrow \mathbb {R}_{i+1}$
is a diffeomorphism and
![]() $\text { for all } t\in \mathbb {R}_i,$
it satisfies
$\text { for all } t\in \mathbb {R}_i,$
it satisfies
That is to say, the following diagram commutes:

where
![]() $\theta |_{\mathbb {R}_i}=\theta _i$
for
$\theta |_{\mathbb {R}_i}=\theta _i$
for
![]() $i\in \mathbb {Z}$
. Since
$i\in \mathbb {Z}$
. Since
![]() $Df$
preserves the orientation of
$Df$
preserves the orientation of
![]() $E^c$
, each
$E^c$
, each
![]() $\widehat {f}|_{\mathbb {R}_z}$
is strictly increasing. In particular, one has that
$\widehat {f}|_{\mathbb {R}_z}$
is strictly increasing. In particular, one has that
![]() $\widehat {f}(0_i)=t_{i+1}$
for every
$\widehat {f}(0_i)=t_{i+1}$
for every
![]() $i\in \mathbb {Z}$
. Moreover, the map
$i\in \mathbb {Z}$
. Moreover, the map
![]() $\theta \colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow M$
is a normally hyperbolic leaf immersion following [Reference Hirsch, Pugh and Shub19, p. 69], see also [Reference Gan and Shi12, Proposition 4.4].
$\theta \colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow M$
is a normally hyperbolic leaf immersion following [Reference Hirsch, Pugh and Shub19, p. 69], see also [Reference Gan and Shi12, Proposition 4.4].
Remark 2.3. When
![]() $\mathcal {F}^c_{x_0}$
is non-compact, so as
$\mathcal {F}^c_{x_0}$
is non-compact, so as
![]() $\mathcal {F}^c_{x_i}$
for all
$\mathcal {F}^c_{x_i}$
for all
![]() $i\in \mathbb {Z}$
, then
$i\in \mathbb {Z}$
, then
![]() $\theta _i$
is a diffeomorphism, and
$\theta _i$
is a diffeomorphism, and
![]() $\widehat {f}|_{\mathbb {R}_i}\colon \mathbb {R}_i\rightarrow \mathbb {R}_{i+1}$
is defined as
$\widehat {f}|_{\mathbb {R}_i}\colon \mathbb {R}_i\rightarrow \mathbb {R}_{i+1}$
is defined as
![]() $\widehat {f}|_{\mathbb {R}_i}=\theta _{i+1}^{-1}\circ f\circ \theta _i$
. When otherwise
$\widehat {f}|_{\mathbb {R}_i}=\theta _{i+1}^{-1}\circ f\circ \theta _i$
. When otherwise
![]() $\mathcal {F}^c_{x_0}$
is compact, so as
$\mathcal {F}^c_{x_0}$
is compact, so as
![]() $\mathcal {F}^c_{x_i}$
for all
$\mathcal {F}^c_{x_i}$
for all
![]() $i\in \mathbb {Z}$
, then each
$i\in \mathbb {Z}$
, then each
![]() $\theta _i$
can be seen as a universal covering map of
$\theta _i$
can be seen as a universal covering map of
![]() $\mathbb {S}^1$
and
$\mathbb {S}^1$
and
![]() $f\colon \mathcal {F}^c_{x_i}\rightarrow \mathcal {F}^c_{x_{i+1}}$
can be seen as a circle diffeomorphism, thus one can take
$f\colon \mathcal {F}^c_{x_i}\rightarrow \mathcal {F}^c_{x_{i+1}}$
can be seen as a circle diffeomorphism, thus one can take
![]() $\widehat {f}|_{\mathbb {R}_i}\colon \mathbb {R}_i\rightarrow \mathbb {R}_{i+1}$
to be the unique lifting map of
$\widehat {f}|_{\mathbb {R}_i}\colon \mathbb {R}_i\rightarrow \mathbb {R}_{i+1}$
to be the unique lifting map of
![]() $f|_{\mathcal {F}^c_{x_i}}$
that satisfies
$f|_{\mathcal {F}^c_{x_i}}$
that satisfies
![]() $|\widehat {f}(0_i)|<\varepsilon $
. Moreover, in both cases,
$|\widehat {f}(0_i)|<\varepsilon $
. Moreover, in both cases,
![]() $\widehat {f}(0_i)=0_{i+1}$
whenever
$\widehat {f}(0_i)=0_{i+1}$
whenever
![]() $i\leq -1$
or
$i\leq -1$
or
![]() $i\geq n$
.
$i\geq n$
.
Remark 2.4. The reason why we extend the center pseudo-orbit
![]() $\Gamma $
to the bi-infinite one
$\Gamma $
to the bi-infinite one
![]() $\Gamma _\infty $
is that, in this way, one obtains an invariant set
$\Gamma _\infty $
is that, in this way, one obtains an invariant set
![]() $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
of the lifting system
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
of the lifting system
![]() $\widehat {f}$
. However, one could lift the center dynamics as above over a general bi-infinite pseudo-orbit, but we will concentrate on the finite part
$\widehat {f}$
. However, one could lift the center dynamics as above over a general bi-infinite pseudo-orbit, but we will concentrate on the finite part
![]() $\Gamma $
in the following.
$\Gamma $
in the following.
Recall that
![]() $f(x_i)=\theta _{i+1}(t_{i+1})$
which is equivalent to say
$f(x_i)=\theta _{i+1}(t_{i+1})$
which is equivalent to say
![]() $\widehat {f}(0_i)=t_{i+1}$
, with
$\widehat {f}(0_i)=t_{i+1}$
, with
![]() $|t_{i+1}|<\varepsilon \text{for all } i\in \mathbb {Z}$
and in particular
$|t_{i+1}|<\varepsilon \text{for all } i\in \mathbb {Z}$
and in particular
![]() $t_{i+1}=0$
when
$t_{i+1}=0$
when
![]() $i\leq -1$
or
$i\leq -1$
or
![]() $i\geq n$
. The following lemma states that replacing some points if necessary, the center pseudo orbit
$i\geq n$
. The following lemma states that replacing some points if necessary, the center pseudo orbit
![]() $\Gamma $
can be chosen to jump in an ordered way.
$\Gamma $
can be chosen to jump in an ordered way.
Lemma 2.5. Replacing some of the intermediate points in
![]() $\{x_1,x_2\ldots ,x_{n-1}\}$
if necessary, one can assume that the
$\{x_1,x_2\ldots ,x_{n-1}\}$
if necessary, one can assume that the
![]() $\varepsilon $
-center pseudo orbit
$\varepsilon $
-center pseudo orbit
![]() $\Gamma $
from
$\Gamma $
from
![]() $x_0$
to
$x_0$
to
![]() $x_n$
satisfies that all
$x_n$
satisfies that all
![]() $t_i, 1\leq i\leq n$
have the same sign. That is to say, either
$t_i, 1\leq i\leq n$
have the same sign. That is to say, either
![]() $-\varepsilon <t_i\leq 0$
for all
$-\varepsilon <t_i\leq 0$
for all
![]() $1\leq i\leq n$
or
$1\leq i\leq n$
or
![]() $0\leq t_i<\varepsilon $
for all
$0\leq t_i<\varepsilon $
for all
![]() $1\leq i\leq n$
.
$1\leq i\leq n$
.
Proof. Note that
![]() $f(\mathcal {F}^c_{x_i})=\mathcal {F}^c_{x_{i+1}}$
. We split the proof into two cases whether the center leaves are compact or not.
$f(\mathcal {F}^c_{x_i})=\mathcal {F}^c_{x_{i+1}}$
. We split the proof into two cases whether the center leaves are compact or not.
Non-compact case. Assume each
![]() $\mathcal {F}^c_{x_i}, i=0,1,\ldots ,n$
is non-compact and thus diffeomorphic to
$\mathcal {F}^c_{x_i}, i=0,1,\ldots ,n$
is non-compact and thus diffeomorphic to
![]() $\mathbb {R}$
by
$\mathbb {R}$
by
![]() $\theta _i$
. To simplify notation, we define an order ‘
$\theta _i$
. To simplify notation, we define an order ‘
![]() $\leq $
’ on each
$\leq $
’ on each
![]() $\mathcal {F}^c_{x_i}$
inherited from that of
$\mathcal {F}^c_{x_i}$
inherited from that of
![]() $\mathbb {R}$
. To be precise, for every
$\mathbb {R}$
. To be precise, for every
![]() $w,w'\in \mathcal {F}^c_{x_i}$
, one defines
$w,w'\in \mathcal {F}^c_{x_i}$
, one defines
![]() $w\leq w'$
(respectively
$w\leq w'$
(respectively
![]() $w< w'$
) if and only if
$w< w'$
) if and only if
![]() $\theta _i^{-1}(w)\leq \theta _i^{-1}(w')$
(respectively
$\theta _i^{-1}(w)\leq \theta _i^{-1}(w')$
(respectively
![]() $\theta _i^{-1}(w)< \theta _i^{-1}(w')$
).
$\theta _i^{-1}(w)< \theta _i^{-1}(w')$
).
Notice that
![]() $f^i(x_0)\in \mathcal {F}^c_{x_i}$
for each
$f^i(x_0)\in \mathcal {F}^c_{x_i}$
for each
![]() $i=0,1,\ldots ,n$
. If in the trivial case
$i=0,1,\ldots ,n$
. If in the trivial case
![]() $f^n(x_0)= x_{n}$
, then one just takes
$f^n(x_0)= x_{n}$
, then one just takes
![]() $x_i=f^i(x_0)$
for each
$x_i=f^i(x_0)$
for each
![]() $i=1,2,\ldots n-1$
and as a result, every
$i=1,2,\ldots n-1$
and as a result, every
![]() $t_i=0$
. So in the following, without loss of generality, assume that
$t_i=0$
. So in the following, without loss of generality, assume that
![]() $f^n(x_0)< x_{n}$
and the other case where
$f^n(x_0)< x_{n}$
and the other case where
![]() $x_n<f^n(x_0)$
is symmetric. One concludes Lemma 2.5 in the non-compact case from the following claim.
$x_n<f^n(x_0)$
is symmetric. One concludes Lemma 2.5 in the non-compact case from the following claim.
Claim 2.6. Replacing some of the intermediate points in
![]() $\{x_1,x_2,\ldots ,x_{n-1}\}$
if necessary, we can choose
$\{x_1,x_2,\ldots ,x_{n-1}\}$
if necessary, we can choose
![]() $\Gamma $
to satisfy that
$\Gamma $
to satisfy that
![]() $f^{i+1}(x_0)\leq f(x_i)\leq x_{i+1}$
for any
$f^{i+1}(x_0)\leq f(x_i)\leq x_{i+1}$
for any
![]() $0\leq i\leq n-1$
. This implies that
$0\leq i\leq n-1$
. This implies that
![]() $-\varepsilon <t_i\leq 0$
for all
$-\varepsilon <t_i\leq 0$
for all
![]() $1\leq i\leq n$
.
$1\leq i\leq n$
.
Proof of Claim 2.6
By the fact that
![]() $Df$
preserves the orientation of
$Df$
preserves the orientation of
![]() $\mathcal {F}^c$
, the assumption
$\mathcal {F}^c$
, the assumption
![]() $f^n(x_0)< x_{n}$
implies
$f^n(x_0)< x_{n}$
implies
![]() $f^{i}(x_0)< f^{-n+i}(x_n)$
for any
$f^{i}(x_0)< f^{-n+i}(x_n)$
for any
![]() $i=0,1,\ldots , n$
.
$i=0,1,\ldots , n$
.
We associate to the center pseudo orbit
![]() $\Gamma =\{x_0,x_1,\ldots ,x_n\}$
an integer
$\Gamma =\{x_0,x_1,\ldots ,x_n\}$
an integer
![]() ${k=k(\Gamma )\in [0,n]}$
defined by the following:
${k=k(\Gamma )\in [0,n]}$
defined by the following:
-
• if
 $f^{n}(x_0)\leq f(x_{n-1})\leq x_{n}$
holds, then k is the smallest integer in
$f^{n}(x_0)\leq f(x_{n-1})\leq x_{n}$
holds, then k is the smallest integer in
 $[0,n-1]$
such that for any
$[0,n-1]$
such that for any
 $i\in [k,n-1]$
, it satisfies
$i\in [k,n-1]$
, it satisfies
 $f^{i+1}(x_0)\leq f(x_i)\leq x_{i+1}$
;
$f^{i+1}(x_0)\leq f(x_i)\leq x_{i+1}$
; -
• if otherwise, take
 $k=n$
.
$k=n$
.
If
![]() $k=k(\Gamma )=0$
, then Claim 2.6 satisfies automatically for
$k=k(\Gamma )=0$
, then Claim 2.6 satisfies automatically for
![]() $\Gamma $
. Thus, in the following, one assumes that
$\Gamma $
. Thus, in the following, one assumes that
![]() $k=k(\Gamma )\geq 1$
.
$k=k(\Gamma )\geq 1$
.
By the choice of k, one knows that the inequality
![]() $f^{k}(x_0)\leq f(x_{k-1})\leq x_{k}$
does not hold. Note that if k is taken as in the first case, then
$f^{k}(x_0)\leq f(x_{k-1})\leq x_{k}$
does not hold. Note that if k is taken as in the first case, then
![]() $f^{k+1}(x_0)\leq f(x_k)$
implies
$f^{k+1}(x_0)\leq f(x_k)$
implies
![]() $f^{k}(x_0)\leq x_k$
; and if in the second case where
$f^{k}(x_0)\leq x_k$
; and if in the second case where
![]() $k=n$
, then one also has
$k=n$
, then one also has
![]() $f^{k}(x_0)\leq x_k$
by assumption. Thus, considering the orders of
$f^{k}(x_0)\leq x_k$
by assumption. Thus, considering the orders of
![]() $f^{k}(x_0), f(x_{k-1})$
and
$f^{k}(x_0), f(x_{k-1})$
and
![]() $x_{k}$
, there are the following two cases: either
$x_{k}$
, there are the following two cases: either
![]() $f(x_{k-1})<f^k(x_0)\leq x_k$
or
$f(x_{k-1})<f^k(x_0)\leq x_k$
or
![]() $f^k(x_0)\leq x_k<f(x_{k-1})$
.
$f^k(x_0)\leq x_k<f(x_{k-1})$
.
Sub-case (a). If
![]() $f(x_{k-1})<f^k(x_0)\leq x_k$
, the fact
$f(x_{k-1})<f^k(x_0)\leq x_k$
, the fact
![]() $d^c(f(x_{k-1}),x_k)<\varepsilon $
implies
$d^c(f(x_{k-1}),x_k)<\varepsilon $
implies
![]() $d^c(f^k(x_{0}), x_k)<\varepsilon $
. Thus, the new collection
$d^c(f^k(x_{0}), x_k)<\varepsilon $
. Thus, the new collection
is an
![]() $\varepsilon $
-center pseudo orbit that satisfies Claim 2.6 and one just denotes it by
$\varepsilon $
-center pseudo orbit that satisfies Claim 2.6 and one just denotes it by
![]() $\Gamma '$
.
$\Gamma '$
.
Sub-case (b). Now we assume
![]() $f^k(x_0)\leq x_k<f(x_{k-1})$
. By the orientation-preserving property, we have
$f^k(x_0)\leq x_k<f(x_{k-1})$
. By the orientation-preserving property, we have
![]() $f^{-1}(x_k)<x_{k-1}$
and
$f^{-1}(x_k)<x_{k-1}$
and
![]() $x_0\leq f^{-k}(x_k)$
. Thus, there exists a minimal
$x_0\leq f^{-k}(x_k)$
. Thus, there exists a minimal
![]() $j\in [1,k-1]$
such that
$j\in [1,k-1]$
such that
![]() $x_i\leq f^{-k+i}(x_k)$
for any
$x_i\leq f^{-k+i}(x_k)$
for any
![]() $i\in [0,j-1]$
while
$i\in [0,j-1]$
while
![]() $f^{-k+j}(x_k)<x_{j}$
. In particular, when
$f^{-k+j}(x_k)<x_{j}$
. In particular, when
![]() $i=j-1$
, the inequality
$i=j-1$
, the inequality
![]() $x_{j-1}\leq f^{-k+j-1}(x_k)$
implies that
$x_{j-1}\leq f^{-k+j-1}(x_k)$
implies that
![]() $f(x_{j-1})\leq f^{-k+j}(x_k)(<x_j)$
. Thus,
$f(x_{j-1})\leq f^{-k+j}(x_k)(<x_j)$
. Thus,
Consider the new collection
This is an
![]() $\varepsilon $
-center pseudo orbit and on
$\varepsilon $
-center pseudo orbit and on
![]() $\mathcal {F}^c_{x_k}$
, it satisfies that
$\mathcal {F}^c_{x_k}$
, it satisfies that
So we denote the new collection by
![]() $\Gamma "$
in Sub-case (b).
$\Gamma "$
in Sub-case (b).
Note that in Sub-case (b), the newly defined
![]() $\varepsilon $
-center pseudo orbit
$\varepsilon $
-center pseudo orbit
![]() $\Gamma "$
satisfies that
$\Gamma "$
satisfies that
![]() $k(\Gamma ")\leq k(\Gamma )-1<k(\Gamma )$
. Moreover, the two endpoints
$k(\Gamma ")\leq k(\Gamma )-1<k(\Gamma )$
. Moreover, the two endpoints
![]() $x_0$
and
$x_0$
and
![]() $x_n$
are always kept. Since the length of the pseudo orbit is finite, this process ends in finite steps. The final
$x_n$
are always kept. Since the length of the pseudo orbit is finite, this process ends in finite steps. The final
![]() $\varepsilon $
-center pseudo orbit, denoted also by
$\varepsilon $
-center pseudo orbit, denoted also by
![]() $\Gamma '$
as in Sub-case (a), satisfies Claim 2.6.
$\Gamma '$
as in Sub-case (a), satisfies Claim 2.6.
Compact case. Assume each
![]() $\mathcal {F}^c_{x_i}, i=0,1,\ldots ,n$
is compact and thus
$\mathcal {F}^c_{x_i}, i=0,1,\ldots ,n$
is compact and thus
![]() $\theta _i\colon \mathbb {R}_i\rightarrow \mathcal {F}^c_{x_i}$
is a universal covering map. By the locally isometric property of
$\theta _i\colon \mathbb {R}_i\rightarrow \mathcal {F}^c_{x_i}$
is a universal covering map. By the locally isometric property of
![]() $\theta _i$
, one can see that the piece
$\theta _i$
, one can see that the piece
![]() $\widehat {\Gamma }=\{0_0,0_1,0_2,\ldots ,0_{n-1},0_n\}$
is an
$\widehat {\Gamma }=\{0_0,0_1,0_2,\ldots ,0_{n-1},0_n\}$
is an
![]() $\varepsilon $
-pseudo orbit of the lifting dynamics
$\varepsilon $
-pseudo orbit of the lifting dynamics
![]() $\widehat {f}$
, where
$\widehat {f}$
, where
![]() $0_i\in \mathbb {R}_i$
is the zero point on
$0_i\in \mathbb {R}_i$
is the zero point on
![]() $\mathbb {R}_i$
for any
$\mathbb {R}_i$
for any
![]() $i=0,1,\ldots ,n$
. Note that
$i=0,1,\ldots ,n$
. Note that
![]() $\widehat {f}(0_i)=t_{i+1}$
. Applying the same arguments as in the non-compact case, one can assume that all
$\widehat {f}(0_i)=t_{i+1}$
. Applying the same arguments as in the non-compact case, one can assume that all
![]() $t_i,1\geq n$
have the same sign. This completes the proof of Lemma 2.5.
$t_i,1\geq n$
have the same sign. This completes the proof of Lemma 2.5.
Remark 2.7. Since each
![]() $\widehat {f}|_{\mathbb {R}_i}$
is strictly increasing, thus, when
$\widehat {f}|_{\mathbb {R}_i}$
is strictly increasing, thus, when
![]() $\Gamma $
is taken to satisfy that
$\Gamma $
is taken to satisfy that
![]() $-\varepsilon <t_i\leq 0$
for all
$-\varepsilon <t_i\leq 0$
for all
![]() $1\leq i\leq n$
as in Lemma 2.5, then
$1\leq i\leq n$
as in Lemma 2.5, then
![]() $\widehat {f}^i(0_0)\leq 0_i$
for all
$\widehat {f}^i(0_0)\leq 0_i$
for all
![]() $1\leq i\leq n$
. The other case is symmetric.
$1\leq i\leq n$
. The other case is symmetric.
One fixes the constants
![]() $0<\unicode{x3bb} <1$
and
$0<\unicode{x3bb} <1$
and
![]() $0<\eta _0<1/10^{-3}$
from §2.1 and
$0<\eta _0<1/10^{-3}$
from §2.1 and
![]() $0<\varepsilon _0<1$
in §2.2.
$0<\varepsilon _0<1$
in §2.2.
2.3 Lifting bundle
Recall that we have fixed two
![]() $C^\infty $
-sub-bundles
$C^\infty $
-sub-bundles
![]() $F^s$
and
$F^s$
and
![]() $F^u$
that are
$F^u$
that are
![]() $C^0$
-close to
$C^0$
-close to
![]() $E^s$
and
$E^s$
and
![]() $E^u$
, respectively. In this section, for a bi-infinite center pseudo orbit
$E^u$
, respectively. In this section, for a bi-infinite center pseudo orbit
![]() $\Gamma $
, we pull back the bundle
$\Gamma $
, we pull back the bundle
![]() $F^s\oplus F^u$
over M to
$F^s\oplus F^u$
over M to
![]() $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
through the
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
through the
![]() $C^1$
-immersion map
$C^1$
-immersion map
![]() $\theta \colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow M$
. Then we obtain a tubular neighborhood of
$\theta \colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow M$
. Then we obtain a tubular neighborhood of
![]() $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
on which one could define an exponential map to M and a bundle map which is partially hyperbolic. The construction follows essentially from [Reference Gan and Shi12, §4.1] where the ideas originates from [Reference Hirsch, Pugh and Shub19]. We sketch the arguments and conclusions here. Also some of the notation is borrowed from [Reference Gan and Shi12].
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
on which one could define an exponential map to M and a bundle map which is partially hyperbolic. The construction follows essentially from [Reference Gan and Shi12, §4.1] where the ideas originates from [Reference Hirsch, Pugh and Shub19]. We sketch the arguments and conclusions here. Also some of the notation is borrowed from [Reference Gan and Shi12].
Assume
![]() $\varepsilon \in (0,\varepsilon _0)$
and let
$\varepsilon \in (0,\varepsilon _0)$
and let
![]() $\Gamma =\{x_0,x_1,\ldots ,x_n\}$
be an
$\Gamma =\{x_0,x_1,\ldots ,x_n\}$
be an
![]() $\varepsilon $
-center pseudo orbit from §2.2 that satisfies Lemma 2.5. Let
$\varepsilon $
-center pseudo orbit from §2.2 that satisfies Lemma 2.5. Let
![]() $\Gamma _\infty =\{x_i\}_{i=-\infty }^{+\infty }$
be the extended bi-infinite center pseudo orbit such that
$\Gamma _\infty =\{x_i\}_{i=-\infty }^{+\infty }$
be the extended bi-infinite center pseudo orbit such that
![]() $x_i=f^i(x_0)$
when
$x_i=f^i(x_0)$
when
![]() $i\leq -1$
and
$i\leq -1$
and
![]() $x_i=f^{i-n}(x_n)$
when
$x_i=f^{i-n}(x_n)$
when
![]() $i\geq n+1$
as in §2.2. One pulls back the
$i\geq n+1$
as in §2.2. One pulls back the
![]() $C^\infty $
-bundle
$C^\infty $
-bundle
![]() $F^s\oplus F^u$
over M by the
$F^s\oplus F^u$
over M by the
![]() $C^1$
-leaf immersion
$C^1$
-leaf immersion
![]() $\theta \colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow M$
to get a fiber bundle
$\theta \colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow M$
to get a fiber bundle
![]() $\theta ^*(F^s\oplus F^u)$
over
$\theta ^*(F^s\oplus F^u)$
over
![]() $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
. Thus, one has the following commuting diagram:
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
. Thus, one has the following commuting diagram:

For each
![]() $t\in \mathbb {R}_i$
where
$t\in \mathbb {R}_i$
where
![]() $i\in \mathbb {Z}$
, one pulls back the Riemannian metric on
$i\in \mathbb {Z}$
, one pulls back the Riemannian metric on
![]() $F^s_{\theta _i(t)}\oplus F^u_{\theta _i(t)}$
and thus the fiber
$F^s_{\theta _i(t)}\oplus F^u_{\theta _i(t)}$
and thus the fiber
over
![]() $t\in \mathbb {R}_i$
is a linear space equipped with an inner product structure. In this way, one defines a metric
$t\in \mathbb {R}_i$
is a linear space equipped with an inner product structure. In this way, one defines a metric
![]() $\|\cdot \|_t$
on
$\|\cdot \|_t$
on
![]() $\theta ^*(F^s\oplus F^u)_t$
. For any constant
$\theta ^*(F^s\oplus F^u)_t$
. For any constant
![]() $\delta>0$
, any
$\delta>0$
, any
![]() $t\in \mathbb {R}_i$
, and any interval
$t\in \mathbb {R}_i$
, and any interval
![]() $I\subset \mathbb {R}_i$
, one denotes
$I\subset \mathbb {R}_i$
, one denotes
and
 $$ \begin{align*}\theta^*(F^s\oplus F^u)(\delta)=\bigcup_{t\in \bigsqcup_{i\in\mathbb{Z}}\mathbb{R}_i}\theta^*(F^s\oplus F^u)_t(\delta).\end{align*} $$
$$ \begin{align*}\theta^*(F^s\oplus F^u)(\delta)=\bigcup_{t\in \bigsqcup_{i\in\mathbb{Z}}\mathbb{R}_i}\theta^*(F^s\oplus F^u)_t(\delta).\end{align*} $$
In particular, when
![]() $\delta =0$
, the
$\delta =0$
, the
![]() $0$
-section
$0$
-section
![]() $\theta ^*(F^s\oplus F^u)(0)$
is reduced to
$\theta ^*(F^s\oplus F^u)(0)$
is reduced to
![]() $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
.
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
.
For
![]() $t\in \mathbb {R}_i$
and
$t\in \mathbb {R}_i$
and
![]() $v\in \theta ^*(F^s\oplus F^u)_t$
, let
$v\in \theta ^*(F^s\oplus F^u)_t$
, let
In this way, one defines the exponential map
![]() $\Phi \colon \theta ^*(F^s\oplus F^u)\rightarrow M$
. Then by [Reference Gan and Shi12, Proposition 4.5], there exists a constant
$\Phi \colon \theta ^*(F^s\oplus F^u)\rightarrow M$
. Then by [Reference Gan and Shi12, Proposition 4.5], there exists a constant
![]() $\delta _0>0$
that depends only on
$\delta _0>0$
that depends only on
![]() $f,F^s,F^u$
such that for any
$f,F^s,F^u$
such that for any
![]() $0<\delta \leq \delta _0$
and for any
$0<\delta \leq \delta _0$
and for any
![]() $t\in \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
, the set
$t\in \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
, the set
![]() $\Phi (\theta ^*(F^s\oplus F^u)_{(t-\delta ,t+\delta )}(\delta ))$
is open in M. Moreover, the exponential map
$\Phi (\theta ^*(F^s\oplus F^u)_{(t-\delta ,t+\delta )}(\delta ))$
is open in M. Moreover, the exponential map
![]() $\Phi $
is a diffeomorphism from
$\Phi $
is a diffeomorphism from
![]() $\theta ^*(F^s\oplus F^u)_{(t-\delta ,t+\delta )}(\delta )$
to its image. As a consequence, there exists a constant
$\theta ^*(F^s\oplus F^u)_{(t-\delta ,t+\delta )}(\delta )$
to its image. As a consequence, there exists a constant
![]() $C_0>1$
that depends on f such that for any
$C_0>1$
that depends on f such that for any
![]() $t\in \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
and any
$t\in \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
and any
![]() $v\in \theta ^*(F^s\oplus F^u)_{t}(\delta _0/C_0)$
, there exists a unique vector
$v\in \theta ^*(F^s\oplus F^u)_{t}(\delta _0/C_0)$
, there exists a unique vector
where
![]() $\Phi ^{-1}$
is defined from
$\Phi ^{-1}$
is defined from
![]() $\Phi (\theta ^*(F^s\oplus F^u)_{(t-\delta _0,t+\delta _0)}(\delta _0))$
to
$\Phi (\theta ^*(F^s\oplus F^u)_{(t-\delta _0,t+\delta _0)}(\delta _0))$
to
![]() $\theta ^*(F^s\oplus F^u)_{(t-\delta _0,t+\delta _0)}(\delta _0)$
. That is to say, one has the following commuting diagram:
$\theta ^*(F^s\oplus F^u)_{(t-\delta _0,t+\delta _0)}(\delta _0)$
. That is to say, one has the following commuting diagram:

Moreover, the lifting map
![]() $\theta ^*f$
is a diffeomorphism from
$\theta ^*f$
is a diffeomorphism from
![]() $\theta ^*(F^s\oplus F^u)(\delta _0/C_0)$
to its image. However, one pulls back the Riemannian metric on M through
$\theta ^*(F^s\oplus F^u)(\delta _0/C_0)$
to its image. However, one pulls back the Riemannian metric on M through
![]() $\Phi $
to obtain a local metric
$\Phi $
to obtain a local metric
![]() $\widetilde {d}(\cdot ,\cdot )$
on
$\widetilde {d}(\cdot ,\cdot )$
on
![]() $\theta ^*(F^s\oplus F^u)(\delta _0)$
. To be precise, for any two
$\theta ^*(F^s\oplus F^u)(\delta _0)$
. To be precise, for any two
![]() $v_1,v_2\in \theta ^*(F^s\oplus F^u)_{(t-\delta _0,t+\delta _0)}(\delta _0)$
for some
$v_1,v_2\in \theta ^*(F^s\oplus F^u)_{(t-\delta _0,t+\delta _0)}(\delta _0)$
for some
![]() $t\in \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
, one has
$t\in \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
, one has
![]() $\widetilde {d}(v_1,v_2)=d(\Phi (v_1),\Phi (v_2))$
. See similar statements in [Reference Gan and Shi12, pp. 32].
$\widetilde {d}(v_1,v_2)=d(\Phi (v_1),\Phi (v_2))$
. See similar statements in [Reference Gan and Shi12, pp. 32].
Remark 2.8. When restricted to the
![]() $0$
-section
$0$
-section
![]() $\theta ^*(F^s\oplus F^u)(0)$
(which is
$\theta ^*(F^s\oplus F^u)(0)$
(which is
![]() $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
as pointed out above), the map
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
as pointed out above), the map
is reduced to
![]() $\widehat {f}\colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
. In this sense, the map
$\widehat {f}\colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
. In this sense, the map
![]() $\theta ^*f$
is in fact an extension of
$\theta ^*f$
is in fact an extension of
![]() $\widehat {f}$
to a tubular neighborhood of
$\widehat {f}$
to a tubular neighborhood of
![]() $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
. Thus, in the following, we identify the
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
. Thus, in the following, we identify the
![]() $0$
-section
$0$
-section
![]() $\theta ^*(F^s\oplus F^u)(0)$
to
$\theta ^*(F^s\oplus F^u)(0)$
to
![]() $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
and associate the order on
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
and associate the order on
![]() $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
to
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
to
![]() $\theta ^*(F^s\oplus F^u)(0)$
. One has
$\theta ^*(F^s\oplus F^u)(0)$
. One has
Remark 2.9. We point out that [Reference Gan and Shi12, Proposition 4.5] deals with periodic center leaves while here we consider general ones. However, the existence of
![]() $\delta _0$
and
$\delta _0$
and
![]() $C_0$
only depends on the uniform hyperbolicity of the two extreme bundles
$C_0$
only depends on the uniform hyperbolicity of the two extreme bundles
![]() $E^s/E^u$
(or equivalently on the constant
$E^s/E^u$
(or equivalently on the constant
![]() $0<\unicode{x3bb} <1$
) and the bounded norm of f.
$0<\unicode{x3bb} <1$
) and the bounded norm of f.
The partially hyperbolic splitting
![]() $TM=E^s\oplus E^c\oplus E^u$
induces a partially hyperbolic structure for the bundle map
$TM=E^s\oplus E^c\oplus E^u$
induces a partially hyperbolic structure for the bundle map
![]() $\theta ^*f\colon \theta ^*(F^s\oplus F^u)(\delta _0/C_0)\rightarrow \theta ^*(F^s\oplus F^u)(\delta _0/2)$
over the diffeomorphism
$\theta ^*f\colon \theta ^*(F^s\oplus F^u)(\delta _0/C_0)\rightarrow \theta ^*(F^s\oplus F^u)(\delta _0/2)$
over the diffeomorphism
![]() $\widehat {f}\colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
with partially hyperbolic splitting
$\widehat {f}\colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
with partially hyperbolic splitting
 $$ \begin{align*} T_{\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i}\theta^*(F^s\oplus F^u) & = \theta^*(E^s)|_{\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i}\oplus T\bigg(\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i\bigg)\oplus \theta^*(E^u)|_{\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i}\\ & = (\theta^*(E^s)\oplus \theta^*(E^c)\oplus \theta^*(E^u))|_{\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i}. \end{align*} $$
$$ \begin{align*} T_{\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i}\theta^*(F^s\oplus F^u) & = \theta^*(E^s)|_{\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i}\oplus T\bigg(\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i\bigg)\oplus \theta^*(E^u)|_{\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i}\\ & = (\theta^*(E^s)\oplus \theta^*(E^c)\oplus \theta^*(E^u))|_{\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i}. \end{align*} $$
The main ingredient is that
![]() $\theta \colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow M$
is a normally hyperbolic immersion following [Reference Hirsch, Pugh and Shub19, p. 69]. The detailed proofs can be found in [Reference Gan and Shi12, Proposition 4.6].
$\theta \colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow M$
is a normally hyperbolic immersion following [Reference Hirsch, Pugh and Shub19, p. 69]. The detailed proofs can be found in [Reference Gan and Shi12, Proposition 4.6].
One fixes the constants
![]() $\delta _0>0$
and
$\delta _0>0$
and
![]() $C_0>1$
from §2.3.
$C_0>1$
from §2.3.
2.4 Lipschitz shadowing of invariant manifolds and leaf conjugancy
Recall that
![]() $X\in \mathcal {X}^r(M)$
is a
$X\in \mathcal {X}^r(M)$
is a
![]() $C^r$
vector field which is positively transverse to
$C^r$
vector field which is positively transverse to
![]() $E^s\oplus E^u$
(and also transverse to
$E^s\oplus E^u$
(and also transverse to
![]() $F^s\oplus F^u$
) everywhere and
$F^s\oplus F^u$
) everywhere and
![]() $X_\tau $
is the time-
$X_\tau $
is the time-
![]() $\tau $
map generated by X. In this section, we consider the lifting bundle map of the composition
$\tau $
map generated by X. In this section, we consider the lifting bundle map of the composition
![]() $X_\tau \circ f$
(which can be seen as
$X_\tau \circ f$
(which can be seen as
![]() $C^r$
-small perturbations of f provided
$C^r$
-small perturbations of f provided
![]() $\tau $
is small). This allows us to have a Lipschitz shadowing property of invariant manifolds (Theorem 2.10) and a leaf conjugacy map (§2.4.1).
$\tau $
is small). This allows us to have a Lipschitz shadowing property of invariant manifolds (Theorem 2.10) and a leaf conjugacy map (§2.4.1).
The transverse property implies that X has no singularity. Denote
![]() $f_\tau =X_\tau \circ f\colon M\rightarrow M$
for every
$f_\tau =X_\tau \circ f\colon M\rightarrow M$
for every
![]() $\tau \in \mathbb {R}$
. One lifts X to be a vector field
$\tau \in \mathbb {R}$
. One lifts X to be a vector field
![]() $\widetilde {X}$
on
$\widetilde {X}$
on
![]() $\theta ^*(F^s\oplus F^u)(\delta _0)$
as follows:
$\theta ^*(F^s\oplus F^u)(\delta _0)$
as follows:
The lifting vector field
![]() $\widetilde {X}$
is
$\widetilde {X}$
is
![]() $C^0$
-continuous on
$C^0$
-continuous on
![]() $\theta ^*(F^s\oplus F^u)(\delta _0)$
, while for
$\theta ^*(F^s\oplus F^u)(\delta _0)$
, while for
![]() $\tau $
small, the time
$\tau $
small, the time
![]() $\tau $
-map
$\tau $
-map
![]() $\widetilde {X}_\tau $
generated by
$\widetilde {X}_\tau $
generated by
![]() $\widetilde {X}$
is a
$\widetilde {X}$
is a
![]() $C^1$
-diffeomorphism from
$C^1$
-diffeomorphism from
![]() $\theta ^*(F^s\oplus F^u)(\delta _0/2)$
to its image in
$\theta ^*(F^s\oplus F^u)(\delta _0/2)$
to its image in
![]() $\theta ^*(F^s\oplus F^u)(\delta _0)$
and satisfies
$\theta ^*(F^s\oplus F^u)(\delta _0)$
and satisfies
![]() $\widetilde {X}_\tau = \Phi ^{-1}\circ X_\tau \circ \Phi $
. One has the following theorem which is stated in [Reference Gan and Shi12, Lemma 4.9, Theorems 4.2 and 4.3], and whose proofs are originated from [Reference Hirsch, Pugh and Shub19, Theorem 6.8] and based on [Reference Hirsch, Pugh and Shub19, Theorem 6.1] which shows the existence and properties of local invariant manifolds. Recall that we have fixed the constant
$\widetilde {X}_\tau = \Phi ^{-1}\circ X_\tau \circ \Phi $
. One has the following theorem which is stated in [Reference Gan and Shi12, Lemma 4.9, Theorems 4.2 and 4.3], and whose proofs are originated from [Reference Hirsch, Pugh and Shub19, Theorem 6.8] and based on [Reference Hirsch, Pugh and Shub19, Theorem 6.1] which shows the existence and properties of local invariant manifolds. Recall that we have fixed the constant
![]() $0<\eta _0<10^{-3}$
from §2.1.
$0<\eta _0<10^{-3}$
from §2.1.
Theorem 2.10. There exist two constants
![]() $\tau _0>0$
and
$\tau _0>0$
and
![]() $L>1$
such that for any
$L>1$
such that for any
![]() $\tau \in [-\tau _0,\tau _0]$
, the following properties are satisfied.
$\tau \in [-\tau _0,\tau _0]$
, the following properties are satisfied.
-
(1) The family of
 $C^1$
-diffeomorphisms
$C^1$
-diffeomorphisms  $$ \begin{align*}\widetilde{f}_\tau=\widetilde{X}_\tau\circ \theta^*f\colon \theta^*(F^s\oplus F^u)(\delta_0/C_0)\rightarrow \theta^*(F^s\oplus F^u)(\delta_0)\end{align*} $$
$$ \begin{align*}\widetilde{f}_\tau=\widetilde{X}_\tau\circ \theta^*f\colon \theta^*(F^s\oplus F^u)(\delta_0/C_0)\rightarrow \theta^*(F^s\oplus F^u)(\delta_0)\end{align*} $$
is well defined and
 $\widetilde {f}_\tau \rightarrow \theta ^*f$
in the
$\widetilde {f}_\tau \rightarrow \theta ^*f$
in the
 $C^1$
-topology as
$C^1$
-topology as
 $\tau \rightarrow 0$
. Moreover, one has
$\tau \rightarrow 0$
. Moreover, one has  $$ \begin{align*}\widetilde{d}(v,\widetilde{X}_\tau(v))\leq L\cdot|\tau|, \quad\text{for all } v\in \theta^*(F^s\oplus F^u)(\delta_0/C_0).\end{align*} $$
$$ \begin{align*}\widetilde{d}(v,\widetilde{X}_\tau(v))\leq L\cdot|\tau|, \quad\text{for all } v\in \theta^*(F^s\oplus F^u)(\delta_0/C_0).\end{align*} $$
-
(2) There exists an
 $\widetilde {f}_\tau $
-invariant
$\widetilde {f}_\tau $
-invariant
 $C^1$
-smooth section
$C^1$
-smooth section
 $\sigma _{\tau }\colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \theta ^*({F}^s\oplus {F}^u)(\delta _0)$
which is defined as and which varies continuously with respect to
$\sigma _{\tau }\colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \theta ^*({F}^s\oplus {F}^u)(\delta _0)$
which is defined as and which varies continuously with respect to $$ \begin{align*}\sigma_{\tau}\bigg(\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i\bigg)= \bigcap_{n\in\mathbb{Z}}\widetilde{f}^n_{\tau} (\theta^*({F}^s\oplus {F}^u)(\delta_0/C_0)),\end{align*} $$
$$ \begin{align*}\sigma_{\tau}\bigg(\bigsqcup\limits_{i\in\mathbb{Z}}\mathbb{R}_i\bigg)= \bigcap_{n\in\mathbb{Z}}\widetilde{f}^n_{\tau} (\theta^*({F}^s\oplus {F}^u)(\delta_0/C_0)),\end{align*} $$
 $\tau $
. The two
$\tau $
. The two
 $C^1$
-manifolds, intersect transversely at
$C^1$
-manifolds, intersect transversely at $$ \begin{align*}W^{cs}_\tau=\bigcap_{n=0}^{+\infty}\widetilde{f}^{-n}_{\tau} (\theta^*({F}^s\oplus {F}^u)(\delta_0/C_0))\quad\text{and}\quad W^{cu}_\tau=\bigcap_{n=0}^{+\infty}\widetilde{f}^{n}_{\tau} (\theta^*({F}^s\oplus {F}^u)(\delta_0/C_0)),\end{align*} $$
$$ \begin{align*}W^{cs}_\tau=\bigcap_{n=0}^{+\infty}\widetilde{f}^{-n}_{\tau} (\theta^*({F}^s\oplus {F}^u)(\delta_0/C_0))\quad\text{and}\quad W^{cu}_\tau=\bigcap_{n=0}^{+\infty}\widetilde{f}^{n}_{\tau} (\theta^*({F}^s\oplus {F}^u)(\delta_0/C_0)),\end{align*} $$
 $\sigma _{\tau }(\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i)=W^{cs}_\tau \cap W^{cu}_\tau $
. Moreover, the section
$\sigma _{\tau }(\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i)=W^{cs}_\tau \cap W^{cu}_\tau $
. Moreover, the section
 $\sigma _\tau $
converges to
$\sigma _\tau $
converges to
 $\sigma _0$
in the
$\sigma _0$
in the
 $C^1$
-topology as
$C^1$
-topology as
 $\tau \rightarrow 0$
, where
$\tau \rightarrow 0$
, where
 $\sigma _0(\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i)=\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
is the
$\sigma _0(\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i)=\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
is the
 $0$
-section.
$0$
-section.
-
(3) For any
 $t\in \mathbb {R}_i, i\in \mathbb {Z}$
and any
$t\in \mathbb {R}_i, i\in \mathbb {Z}$
and any
 $C^1$
map
$C^1$
map
 $\varphi \colon E^s_{\theta _i(t)}(\delta _0)\oplus E^u_{\theta _i(t)}(\delta _0)\rightarrow E^c_{\theta _i(t)}(\delta _0)$
satisfying
$\varphi \colon E^s_{\theta _i(t)}(\delta _0)\oplus E^u_{\theta _i(t)}(\delta _0)\rightarrow E^c_{\theta _i(t)}(\delta _0)$
satisfying
 $\varphi (0)=0, \|\partial \varphi /\partial \alpha \|\leq \eta _0$
for
$\varphi (0)=0, \|\partial \varphi /\partial \alpha \|\leq \eta _0$
for
 $\alpha =s,u$
, the
$\alpha =s,u$
, the
 $C^1$
-submanifold intersects
$C^1$
-submanifold intersects $$ \begin{align*}D^{su}_{\theta_i(t)}&=\exp_{\theta_i(t)}(\operatorname{Graph}(\varphi))\\&= \exp_{\theta_i(t)}(\{v^{su}+\varphi(v^{su})\colon v^{su}\in E^s_{\theta_i(t)}(\delta_0)\oplus E^u_{\theta_i(t)}(\delta_0)\})\end{align*} $$
$$ \begin{align*}D^{su}_{\theta_i(t)}&=\exp_{\theta_i(t)}(\operatorname{Graph}(\varphi))\\&= \exp_{\theta_i(t)}(\{v^{su}+\varphi(v^{su})\colon v^{su}\in E^s_{\theta_i(t)}(\delta_0)\oplus E^u_{\theta_i(t)}(\delta_0)\})\end{align*} $$
 $\Phi (\sigma _{\tau }((t-\delta _0,t+\delta _0)))$
at a unique point
$\Phi (\sigma _{\tau }((t-\delta _0,t+\delta _0)))$
at a unique point
 $q=q(t,\tau ,\varphi )$
. Moreover, let
$q=q(t,\tau ,\varphi )$
. Moreover, let
 $v_q^{su}\in E^s_{\theta _i(t)}(\delta _0)\oplus E^u_{\theta _i(t)}(\delta _0)$
be such that
$v_q^{su}\in E^s_{\theta _i(t)}(\delta _0)\oplus E^u_{\theta _i(t)}(\delta _0)$
be such that
 $q=\exp _{\theta _i(t)}(v_q^{su}+\varphi (v_q^{su}))$
, then which in particular implies that
$q=\exp _{\theta _i(t)}(v_q^{su}+\varphi (v_q^{su}))$
, then which in particular implies that $$ \begin{align*}\|v_q^{su}\|+\|\varphi(v_q^{su})\|\leq L\cdot|\tau|,\end{align*} $$
$$ \begin{align*}\|v_q^{su}\|+\|\varphi(v_q^{su})\|\leq L\cdot|\tau|,\end{align*} $$
 $\sigma _{\tau }(\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i)\subset \theta ^*(F^s\oplus F^u)(L\cdot |\tau |)$
.
$\sigma _{\tau }(\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i)\subset \theta ^*(F^s\oplus F^u)(L\cdot |\tau |)$
.
Remark 2.11. Note that the map
![]() $\widetilde {f}_\tau =\widetilde {X}_\tau \circ \theta ^*f$
in Theorem 2.10 is the lift of
$\widetilde {f}_\tau =\widetilde {X}_\tau \circ \theta ^*f$
in Theorem 2.10 is the lift of
![]() ${f_\tau =X_\tau \circ f}$
. In particular, when
${f_\tau =X_\tau \circ f}$
. In particular, when
![]() $\tau =0$
, one has
$\tau =0$
, one has
![]() $\widetilde {f}_0=\theta ^*f$
and as a consequence (recall Remark 2.8), when restricted to the
$\widetilde {f}_0=\theta ^*f$
and as a consequence (recall Remark 2.8), when restricted to the
![]() $0$
-section
$0$
-section
![]() $\theta ^*({F}^s\oplus {F}^u)(0)=\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
, it satisfies:
$\theta ^*({F}^s\oplus {F}^u)(0)=\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
, it satisfies:
2.4.1 Leaf conjugacy
Given a constant
![]() $\eta \in (0,\eta _0]$
and an
$\eta \in (0,\eta _0]$
and an
![]() $(s+u)$
-dimensional
$(s+u)$
-dimensional
![]() $C^\infty $
-sub-bundle F of
$C^\infty $
-sub-bundle F of
![]() $TM$
that is
$TM$
that is
![]() $\eta $
-
$\eta $
-
![]() $C^0$
-close to
$C^0$
-close to
![]() $E^s\oplus E^u$
. For a point
$E^s\oplus E^u$
. For a point
![]() $z\in M$
and a constant
$z\in M$
and a constant
![]() $0<\delta \leq \delta _0$
, let
$0<\delta \leq \delta _0$
, let
Then following the arguments in [Reference Gan and Shi12, §4.2] (different to our setting here, as [Reference Gan and Shi12, §4.2] deals with a bundle
![]() $E^s\oplus F$
where
$E^s\oplus F$
where
![]() $E^s$
is the contracting sub-bundle in the partially hyperbolic splitting and F is an u-dimensional
$E^s$
is the contracting sub-bundle in the partially hyperbolic splitting and F is an u-dimensional
![]() $C^\infty $
-sub-bundle that is
$C^\infty $
-sub-bundle that is
![]() $C^0$
-close to the expanding sub-bundle
$C^0$
-close to the expanding sub-bundle
![]() $E^u$
), there exists a constant
$E^u$
), there exists a constant
![]() $\delta _1=\delta _1(F,\eta )\in (0,\delta _0]$
such that the following properties are satisfied.
$\delta _1=\delta _1(F,\eta )\in (0,\delta _0]$
such that the following properties are satisfied.
-
(1) For any point
 $z\in M$
, the set
$z\in M$
, the set
 $D^{F}_z(\delta _1)$
is a
$D^{F}_z(\delta _1)$
is a
 $C^r$
-smooth local manifold whose tangent bundle is
$C^r$
-smooth local manifold whose tangent bundle is
 $2\eta $
-close to
$2\eta $
-close to
 $E^s\oplus E^u$
. To be precise,
$E^s\oplus E^u$
. To be precise,  $$ \begin{align*}\angle(T_wD^{F}_z(\delta_1),(E^s\oplus E^u)_w)<2\eta,\quad\text{for all } w\in D^{F}_z(\delta_1).\end{align*} $$
$$ \begin{align*}\angle(T_wD^{F}_z(\delta_1),(E^s\oplus E^u)_w)<2\eta,\quad\text{for all } w\in D^{F}_z(\delta_1).\end{align*} $$
As a consequence, there exists a
 $C^r$
-map
$C^r$
-map
 $\varphi ^{su}_z\colon E^s(\delta _1/2)\oplus E^u(\delta _1/2)\rightarrow E^c(\delta _1/2)$
satisfying that:
$\varphi ^{su}_z\colon E^s(\delta _1/2)\oplus E^u(\delta _1/2)\rightarrow E^c(\delta _1/2)$
satisfying that:-
•
 $\operatorname {Graph}(\varphi ^{su}_z)=\exp ^{-1}(D^{F}_z(\delta _1))\cap T_zM(\delta _1/2)$
;
$\operatorname {Graph}(\varphi ^{su}_z)=\exp ^{-1}(D^{F}_z(\delta _1))\cap T_zM(\delta _1/2)$
; -
•
 $\varphi ^{su}_z(0_z^{su})=0_z^c$
and
$\varphi ^{su}_z(0_z^{su})=0_z^c$
and
 $\|\partial \varphi ^{su}_z/\partial \alpha \|<2\eta $
for
$\|\partial \varphi ^{su}_z/\partial \alpha \|<2\eta $
for
 $\alpha =s,u$
.
$\alpha =s,u$
.
-
-
(2) Given a
 $C^1$
-center curve
$C^1$
-center curve
 $\gamma ^c$
with radius
$\gamma ^c$
with radius
 $\delta _1$
and centered at a point
$\delta _1$
and centered at a point
 $z\in M$
, the set is a neighborhood of z in M and the family
$z\in M$
, the set is a neighborhood of z in M and the family $$ \begin{align*}B^{F}_{z}(\gamma^c,\delta_1)=\bigcup_{w\in\gamma^c} D^{F}_w(\delta_1)\end{align*} $$
forms a
$$ \begin{align*}B^{F}_{z}(\gamma^c,\delta_1)=\bigcup_{w\in\gamma^c} D^{F}_w(\delta_1)\end{align*} $$
forms a $$ \begin{align*}\mathcal{D}^{F}(\gamma^c)=\{D^{F}_w(\delta_1)\colon w\in\gamma^c \}\end{align*} $$
$$ \begin{align*}\mathcal{D}^{F}(\gamma^c)=\{D^{F}_w(\delta_1)\colon w\in\gamma^c \}\end{align*} $$
 $C^0$
-foliation of
$C^0$
-foliation of
 $B^{F}_{z}(\delta _1)$
. Moreover, the foliation
$B^{F}_{z}(\delta _1)$
. Moreover, the foliation
 $\mathcal {D}^{F}(\gamma ^c)$
is transverse to any
$\mathcal {D}^{F}(\gamma ^c)$
is transverse to any
 $C^1$
-curve
$C^1$
-curve
 $\gamma \in B^{F}_{z}(\delta _1)$
that is tangent to the
$\gamma \in B^{F}_{z}(\delta _1)$
that is tangent to the
 $\eta $
-cone filed of
$\eta $
-cone filed of
 $E^c$
.
$E^c$
.
-
(3) By the uniform transversality and compactness, for any constant
 $\delta \in [0,\delta _1]$
, there exists
$\delta \in [0,\delta _1]$
, there exists
 $\delta '\in [0,\delta _1]$
such that given a
$\delta '\in [0,\delta _1]$
such that given a
 $C^1$
-center curve
$C^1$
-center curve
 $\gamma ^c$
with radius
$\gamma ^c$
with radius
 $\delta _1$
and centered at a point
$\delta _1$
and centered at a point
 $z\in M$
, if
$z\in M$
, if
 $\gamma _1$
and
$\gamma _1$
and
 $\gamma _2$
are two
$\gamma _2$
are two
 $C^1$
-curves tangent to the
$C^1$
-curves tangent to the
 $\eta _0$
-cone field of
$\eta _0$
-cone field of
 $E^c$
in
$E^c$
in
 $B^{F}_{z}(\gamma ^c,\delta _1)$
with endpoints
$B^{F}_{z}(\gamma ^c,\delta _1)$
with endpoints
 $w_i,w_i',i=1,2$
that satisfy then
$w_i,w_i',i=1,2$
that satisfy then $$ \begin{align*}w_1,w_2\in D^{F}_{w_0}(\delta_1)~~\text{and}~~w_1',w_2'\in D^{F}_{w_0'}(\delta_1)~~\text{where}~~w_0,w_0'\in\gamma^c,\end{align*} $$
$$ \begin{align*}w_1,w_2\in D^{F}_{w_0}(\delta_1)~~\text{and}~~w_1',w_2'\in D^{F}_{w_0'}(\delta_1)~~\text{where}~~w_0,w_0'\in\gamma^c,\end{align*} $$
 $\operatorname {length}(\gamma _1)\geq \delta $
implies
$\operatorname {length}(\gamma _1)\geq \delta $
implies
 $\operatorname {length}(\gamma _2)\geq \delta '$
.
$\operatorname {length}(\gamma _2)\geq \delta '$
.
Denote
![]() $\widetilde {D}^{F}_t(\delta )=\Phi ^{-1}(D^{F}_{\theta (t)}(\delta ))$
for
$\widetilde {D}^{F}_t(\delta )=\Phi ^{-1}(D^{F}_{\theta (t)}(\delta ))$
for
![]() $0<\delta <\delta _1$
. Then
$0<\delta <\delta _1$
. Then
 $$ \begin{align*}\mathcal{D}^{F}(\delta_1/10)=\bigg\{\widetilde{D}^{F}_t(\delta)\cap \theta^*(F^s\oplus F^u)(\delta_1/10)\colon t\in\bigsqcup_{i\in\mathbb{Z}} \mathbb{R}_i\bigg\}\end{align*} $$
$$ \begin{align*}\mathcal{D}^{F}(\delta_1/10)=\bigg\{\widetilde{D}^{F}_t(\delta)\cap \theta^*(F^s\oplus F^u)(\delta_1/10)\colon t\in\bigsqcup_{i\in\mathbb{Z}} \mathbb{R}_i\bigg\}\end{align*} $$
forms a
![]() $C^0$
-foliation of
$C^0$
-foliation of
![]() $\theta ^*(F^s\oplus F^u)(\delta _1/10)$
that is transverse to
$\theta ^*(F^s\oplus F^u)(\delta _1/10)$
that is transverse to
![]() $(\Phi ^{-1})^*(E^c)$
everywhere. Following the idea of [Reference Hirsch, Pugh and Shub19, §7], one can define a leaf conjugacy as follows. There exists a constant
$(\Phi ^{-1})^*(E^c)$
everywhere. Following the idea of [Reference Hirsch, Pugh and Shub19, §7], one can define a leaf conjugacy as follows. There exists a constant
![]() $\tau _1=\tau _1(\eta ,F,\delta _1)\in (0,\tau _0]$
where
$\tau _1=\tau _1(\eta ,F,\delta _1)\in (0,\tau _0]$
where
![]() $\tau _0$
is from Theorem 2.10, such that for every
$\tau _0$
is from Theorem 2.10, such that for every
![]() $\tau \in [-\tau _1,\tau _1]$
, the leaf conjugacy
$\tau \in [-\tau _1,\tau _1]$
, the leaf conjugacy
where
is well defined. In particular, when
![]() $\tau =0$
, the map
$\tau =0$
, the map
![]() $h_0|_{\mathbb {R}_i}$
is the identity map
$h_0|_{\mathbb {R}_i}$
is the identity map
![]() $\operatorname {Id}|_{\mathbb {R}_i}$
.
$\operatorname {Id}|_{\mathbb {R}_i}$
.
The constant
![]() $\eta $
and the bundle F (thus
$\eta $
and the bundle F (thus
![]() $\delta _1=\delta _1(\eta ,F)$
and
$\delta _1=\delta _1(\eta ,F)$
and
![]() $\tau _1=\tau _1(\eta ,F,\delta _1)$
) will be determined in Proposition 3.1 in the next section.
$\tau _1=\tau _1(\eta ,F,\delta _1)$
) will be determined in Proposition 3.1 in the next section.
3 Proofs of main theorems
In this section, we prove Theorem A and Corollary B. Let
![]() $f\in \operatorname {DPH}_1^r(M)$
,
$f\in \operatorname {DPH}_1^r(M)$
,
![]() $r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
and
$r\in \mathbb {N}_{\geq 2}\cup \{\infty \}$
and
![]() $X\in \mathcal {X}^r(M)$
be a vector field that is positively transverse to
$X\in \mathcal {X}^r(M)$
be a vector field that is positively transverse to
![]() $E^s\oplus E^u$
. For the proof of Theorem A, all the settings and assumptions are taken from §2.
$E^s\oplus E^u$
. For the proof of Theorem A, all the settings and assumptions are taken from §2.
3.1 A global perturbation along the center direction
One has the following proposition that realizes perturbations along center directions. The idea essentially follows from arguments in [Reference Gan and Shi12, Proposition 4.17] with the difference that [Reference Gan and Shi12, Proposition 4.17] deals with periodic leaves while here we consider general cases. We will include the proof for completeness. Recall in Remarks 2.8 and 2.11, the
![]() $0$
-section
$0$
-section
![]() $\theta ^*({F}^s\oplus {F}^u)(0)$
is identified to be
$\theta ^*({F}^s\oplus {F}^u)(0)$
is identified to be
![]() $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
and thus is associated with an order from
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
and thus is associated with an order from
![]() $\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
. Also restricted on
$\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i$
. Also restricted on
![]() $\theta ^*({F}^s\oplus {F}^u)(0)$
, one has
$\theta ^*({F}^s\oplus {F}^u)(0)$
, one has
![]() $\widetilde {f}_0|_{\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i} = \theta ^*f|_{\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i}=\widehat {f}$
.
$\widetilde {f}_0|_{\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i} = \theta ^*f|_{\bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i}=\widehat {f}$
.
Proposition 3.1. There exist a constant
![]() $\eta =\eta (f,X)\in (0,\eta _0]$
, an
$\eta =\eta (f,X)\in (0,\eta _0]$
, an
![]() $(s+u)$
-dimensional
$(s+u)$
-dimensional
![]() $C^\infty $
sub-bundle
$C^\infty $
sub-bundle
![]() $F\subset TM$
that is
$F\subset TM$
that is
![]() $\eta $
-close to
$\eta $
-close to
![]() $E^s\oplus E^u$
and
$E^s\oplus E^u$
and
![]() $\tau _2=\tau _2(f,X,\eta ,F)\in (0,\tau _1]$
such that the following properties are satisfied. For
$\tau _2=\tau _2(f,X,\eta ,F)\in (0,\tau _1]$
such that the following properties are satisfied. For
![]() $\tau \in [-\tau _2,\tau _2]$
, let
$\tau \in [-\tau _2,\tau _2]$
, let
![]() $h_\tau \colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \bigsqcup \nolimits _{i\in \mathbb {Z}}\sigma _\tau (\mathbb {R}_i)$
be the leaf conjugacy
$h_\tau \colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \bigsqcup \nolimits _{i\in \mathbb {Z}}\sigma _\tau (\mathbb {R}_i)$
be the leaf conjugacy
then for any
![]() $\tau \in [-\tau _2,\tau _2]$
, there exists
$\tau \in [-\tau _2,\tau _2]$
, there exists
![]() $\Delta _\tau>0$
such that for any
$\Delta _\tau>0$
such that for any
![]() $t\in \mathbb {R}_i$
, one has:
$t\in \mathbb {R}_i$
, one has:
-
(1) if
 $0<\tau <\tau _2$
, then
$0<\tau <\tau _2$
, then  $$ \begin{align*}\widetilde{f}_{\tau}\circ h_\tau(t)>h_\tau(\theta^*f(t)+\Delta_\tau);\end{align*} $$
$$ \begin{align*}\widetilde{f}_{\tau}\circ h_\tau(t)>h_\tau(\theta^*f(t)+\Delta_\tau);\end{align*} $$
-
(2) if
 $-\tau _2<\tau <0$
, then
$-\tau _2<\tau <0$
, then  $$ \begin{align*}\widetilde{f}_{\tau}\circ h_\tau(t)<h_\tau(\theta^*f(t)-\Delta_\tau).\end{align*} $$
$$ \begin{align*}\widetilde{f}_{\tau}\circ h_\tau(t)<h_\tau(\theta^*f(t)-\Delta_\tau).\end{align*} $$
Here the order on each
![]() $\sigma _{\tau }(\mathbb {R}_i)$
is inherited from that on
$\sigma _{\tau }(\mathbb {R}_i)$
is inherited from that on
![]() $\mathbb {R}_i$
. The constants
$\mathbb {R}_i$
. The constants
![]() $\delta _1=\delta _1(\eta ,F)$
and
$\delta _1=\delta _1(\eta ,F)$
and
![]() $\tau _1=\tau _1(\eta ,F,\delta _1)$
are from §2.4.1.
$\tau _1=\tau _1(\eta ,F,\delta _1)$
are from §2.4.1.
Proof. We only prove the case when
![]() $\tau>0$
since the other case when
$\tau>0$
since the other case when
![]() $\tau <0$
is symmetric.
$\tau <0$
is symmetric.
3.1.1 The lifting vector field
 $ \widehat {X}$
on
$ \widehat {X}$
on
 $TM$
$TM$
One first lifts X to
![]() $TM$
in the following way: given a point
$TM$
in the following way: given a point
![]() $z\in M$
, let
$z\in M$
, let
![]() $\widehat {X}_z=D\exp ^{-1}_z(X)$
. Then
$\widehat {X}_z=D\exp ^{-1}_z(X)$
. Then
![]() $\widehat {X}_z$
is a vector field which is well defined in a neighborhood of the zero vector
$\widehat {X}_z$
is a vector field which is well defined in a neighborhood of the zero vector
![]() $0_z\in T_zM$
. Note that for
$0_z\in T_zM$
. Note that for
![]() $v\in T_zM$
, its tangent space
$v\in T_zM$
, its tangent space
![]() $T_v(T_zM)\cong T_zM$
, thus it admits a direct sum
$T_v(T_zM)\cong T_zM$
, thus it admits a direct sum
![]() $T_v(T_zM)=E_z^s(v)\oplus E_z^c(v)\oplus E_z^u(v)$
induced by
$T_v(T_zM)=E_z^s(v)\oplus E_z^c(v)\oplus E_z^u(v)$
induced by
![]() $T_zM=E^s_z\oplus E^c_z\oplus E^u_z$
. For
$T_zM=E^s_z\oplus E^c_z\oplus E^u_z$
. For
![]() $v\in T_zM$
close to
$v\in T_zM$
close to
![]() $0_z$
, denote
$0_z$
, denote
where
![]() $\widehat {X}_z^\alpha (v)\in E_z^\alpha (v), \alpha =s,c,u$
. Recall that X is positively transverse to
$\widehat {X}_z^\alpha (v)\in E_z^\alpha (v), \alpha =s,c,u$
. Recall that X is positively transverse to
![]() $E^s\oplus E^u$
, thus there exist constants
$E^s\oplus E^u$
, thus there exist constants
![]() $\delta _2>0$
,
$\delta _2>0$
,
![]() $a_0>0$
, and
$a_0>0$
, and
![]() $b_0>0$
such that for any
$b_0>0$
such that for any
![]() $z\in M$
:
$z\in M$
:
-
• for any
 $v\in T_zM(\delta _2)=E^s_z(\delta _2)\oplus E^c_z(\delta _2)\oplus E^u_z(\delta _2)$
, it satisfies
$v\in T_zM(\delta _2)=E^s_z(\delta _2)\oplus E^c_z(\delta _2)\oplus E^u_z(\delta _2)$
, it satisfies  $$ \begin{align*}\|\widehat{X}_z^c(v)\|\geq b_0,\quad\text{and}\quad \|\widehat{X}_z^s(v)+\widehat{X}_z^u(v)\|<a_0\|\widehat{X}_z^c(v)\|\leq 2 a_0\|\widehat{X}\|;\end{align*} $$
$$ \begin{align*}\|\widehat{X}_z^c(v)\|\geq b_0,\quad\text{and}\quad \|\widehat{X}_z^s(v)+\widehat{X}_z^u(v)\|<a_0\|\widehat{X}_z^c(v)\|\leq 2 a_0\|\widehat{X}\|;\end{align*} $$
-
• for any
 $v\in E^s_z(\delta _2)\oplus E^u_z(\delta _2)$
, the curve
$v\in E^s_z(\delta _2)\oplus E^u_z(\delta _2)$
, the curve
 $\exp _z(v\times E^c_z(\delta _2))$
is tangent to the
$\exp _z(v\times E^c_z(\delta _2))$
is tangent to the
 $\eta _0$
-cone field of
$\eta _0$
-cone field of
 $E^c$
.
$E^c$
.
Recall that one has defined an order on
![]() $E^c_z$
that is induced from the orientation of
$E^c_z$
that is induced from the orientation of
![]() $E^c$
in §2.1. One thus can associate the order of
$E^c$
in §2.1. One thus can associate the order of
![]() $E^c_z$
to
$E^c_z$
to
![]() $E^c_z(v)$
for each
$E^c_z(v)$
for each
![]() $v\in T_zM$
. Then we have
$v\in T_zM$
. Then we have
![]() $\widehat {X}_z^c(v)\geq b_0>0$
for every vector
$\widehat {X}_z^c(v)\geq b_0>0$
for every vector
![]() $v\in T_zM(\delta _2)$
.
$v\in T_zM(\delta _2)$
.
3.1.2 The choices of constants
 $\eta ,\tau '$
and the
$\eta ,\tau '$
and the
 $C^\infty $
bundle F
$C^\infty $
bundle F
Let
![]() $\tau _0>0$
and
$\tau _0>0$
and
![]() $L>1$
be the two constants given by Theorem 2.10. Now we take the constant
$L>1$
be the two constants given by Theorem 2.10. Now we take the constant
![]() $\eta =\eta (f,X)\in (0,\eta _0]$
and the
$\eta =\eta (f,X)\in (0,\eta _0]$
and the
![]() $(s+u)$
-dimensional
$(s+u)$
-dimensional
![]() $C^\infty $
sub-bundle
$C^\infty $
sub-bundle
![]() $F\subset TM$
as follows.
$F\subset TM$
as follows.
-
• Take
 $\eta $
to satisfy
$\eta $
to satisfy  $$ \begin{align*}0<\eta<\min\bigg\{\eta_0,\frac{b_0}{8\cdot [(\|Df\|+1)\cdot L+ 2 a_0\|\widehat{X}\| ]}\bigg\}.\end{align*} $$
$$ \begin{align*}0<\eta<\min\bigg\{\eta_0,\frac{b_0}{8\cdot [(\|Df\|+1)\cdot L+ 2 a_0\|\widehat{X}\| ]}\bigg\}.\end{align*} $$
-
• Take an
 $(s+u)$
-dimensional
$(s+u)$
-dimensional
 $C^\infty $
sub-bundle
$C^\infty $
sub-bundle
 $F\subset TM$
that is
$F\subset TM$
that is
 $\eta $
-close to
$\eta $
-close to
 $E^s\oplus E^u$
, that is,
$E^s\oplus E^u$
, that is,
 $\angle (F,E^s\oplus E^u)<\eta $
.
$\angle (F,E^s\oplus E^u)<\eta $
.
Associated to
![]() $\eta $
and F, there exist
$\eta $
and F, there exist
![]() $\delta _1=\delta _1(\eta ,F)\in (0,\delta _0]$
and
$\delta _1=\delta _1(\eta ,F)\in (0,\delta _0]$
and
![]() $\tau _1=\tau _1(\eta ,F,\delta _1)\in (0,\tau _0]$
that are from §2.4.1. Set
$\tau _1=\tau _1(\eta ,F,\delta _1)\in (0,\tau _0]$
that are from §2.4.1. Set
![]() $\delta '=10^{-2}\min \{\delta _1,\delta _2\}$
and take a constant
$\delta '=10^{-2}\min \{\delta _1,\delta _2\}$
and take a constant
![]() $\tau '=\tau '(f,X,\eta ,F)\in (0,\tau _0]$
that satisfies
$\tau '=\tau '(f,X,\eta ,F)\in (0,\tau _0]$
that satisfies
 $$ \begin{align*}0<\tau'<\min\bigg\{\tau_1,\frac{\delta'}{100L(\|X\|+1)\|Df\|}\bigg\},\end{align*} $$
$$ \begin{align*}0<\tau'<\min\bigg\{\tau_1,\frac{\delta'}{100L(\|X\|+1)\|Df\|}\bigg\},\end{align*} $$
where
![]() $\|X\|=\sup _{x\in M}\|X(x)\|$
and
$\|X\|=\sup _{x\in M}\|X(x)\|$
and
![]() $\|Df\|=\sup _{x\in M}\|Df(x)\|$
.
$\|Df\|=\sup _{x\in M}\|Df(x)\|$
.
3.1.3 The estimation of moving along the center direction
Fix
![]() $t\in \mathbb {R}_i$
and denote
$t\in \mathbb {R}_i$
and denote
![]() ${z_0=\theta _i(t)}$
. For any
${z_0=\theta _i(t)}$
. For any
![]() $\tau \in [-\tau ',\tau ']$
, let
$\tau \in [-\tau ',\tau ']$
, let
![]() $q_\tau =\Phi (h_\tau (t))$
. By the choices of constants and Theorem 2.10, one has that
$q_\tau =\Phi (h_\tau (t))$
. By the choices of constants and Theorem 2.10, one has that
![]() $q_\tau \in D^F_{z_0}(\delta ')$
. Moreover, considering the direct sum
$q_\tau \in D^F_{z_0}(\delta ')$
. Moreover, considering the direct sum
![]() $\exp ^{-1}(q_\tau )=v_{q_\tau }^{su}+v_{q_\tau }^c\in E^{su}_{z_0}\oplus E^c_{z_0}$
, it satisfies that
$\exp ^{-1}(q_\tau )=v_{q_\tau }^{su}+v_{q_\tau }^c\in E^{su}_{z_0}\oplus E^c_{z_0}$
, it satisfies that
 $$ \begin{align*}\|v_{q_\tau}^{su}\|\leq L\cdot\tau\leq \frac{\delta'}{100(\|X\|+1)\|Df\|}.\end{align*} $$
$$ \begin{align*}\|v_{q_\tau}^{su}\|\leq L\cdot\tau\leq \frac{\delta'}{100(\|X\|+1)\|Df\|}.\end{align*} $$
Let
![]() $\varphi ^{su}_{z_0}\colon E^s_{z_0}(\delta _1/2)\oplus E^u_{z_0}(\delta _1/2)\rightarrow E^c_{z_0}(\delta _1/2)$
be the
$\varphi ^{su}_{z_0}\colon E^s_{z_0}(\delta _1/2)\oplus E^u_{z_0}(\delta _1/2)\rightarrow E^c_{z_0}(\delta _1/2)$
be the
![]() $C^r$
-map satisfying that
$C^r$
-map satisfying that
then one has
 $$ \begin{align*}v_{q_\tau}^c=\varphi^{su}_{z_0}(v_{q_\tau}^{su})<2\eta\cdot\|v_{q_\tau}^{su}\|\leq 2\eta\cdot L\cdot\tau\leq 2\eta\cdot\frac{\delta'}{100(\|X\|+1)\|Df\|}.\end{align*} $$
$$ \begin{align*}v_{q_\tau}^c=\varphi^{su}_{z_0}(v_{q_\tau}^{su})<2\eta\cdot\|v_{q_\tau}^{su}\|\leq 2\eta\cdot L\cdot\tau\leq 2\eta\cdot\frac{\delta'}{100(\|X\|+1)\|Df\|}.\end{align*} $$
Note that
![]() $z_0=\theta _i(t)$
and
$z_0=\theta _i(t)$
and
![]() $f(z_0)=\theta _{i+1}(\theta ^*f(t))$
. By the choices of constants above, for any
$f(z_0)=\theta _{i+1}(\theta ^*f(t))$
. By the choices of constants above, for any
![]() $\tau \in [-\tau ',\tau ']$
, one has
$\tau \in [-\tau ',\tau ']$
, one has
Consider the direct sum
then one has the following claim.
Claim 3.2. There exist a continuous function
![]() $\xi \colon \mathbb {R}\rightarrow \mathbb {R}^+$
that depends on f and X satisfying that:
$\xi \colon \mathbb {R}\rightarrow \mathbb {R}^+$
that depends on f and X satisfying that:
-
(1)
 $\xi (\tau )=\mathrm {o}(\tau )$
as
$\xi (\tau )=\mathrm {o}(\tau )$
as
 $\tau \rightarrow 0$
;
$\tau \rightarrow 0$
; -
(2) the following estimates holds:
-
•
 $\|v_{f(q_\tau )}^{su}\|\leq (\|Df(z_0)\|+\xi (\tau ))\cdot \|v_{q_\tau }^{su}\|\leq (\|Df(z_0)\|+\xi (\tau ))\cdot L\tau $
;
$\|v_{f(q_\tau )}^{su}\|\leq (\|Df(z_0)\|+\xi (\tau ))\cdot \|v_{q_\tau }^{su}\|\leq (\|Df(z_0)\|+\xi (\tau ))\cdot L\tau $
; -
•
 $\|v_{f(q_\tau )}^{c}\|\leq (\|Df|_{E^c_{z_0}}\|+\xi (\tau ))\cdot \|v_{q_\tau }^{c}\|\leq 2\eta \cdot (\|Df|_{E^c_{z_0}}\|+\xi (\tau ))\cdot L\tau .$
$\|v_{f(q_\tau )}^{c}\|\leq (\|Df|_{E^c_{z_0}}\|+\xi (\tau ))\cdot \|v_{q_\tau }^{c}\|\leq 2\eta \cdot (\|Df|_{E^c_{z_0}}\|+\xi (\tau ))\cdot L\tau .$
The second formula implies that
 $$ \begin{align*}v_{f(q_\tau)}^{c}\geq-2\eta\cdot(\|Df|_{E^c_{z_0}}\|+\xi(\tau))\cdot L\tau.\end{align*} $$
$$ \begin{align*}v_{f(q_\tau)}^{c}\geq-2\eta\cdot(\|Df|_{E^c_{z_0}}\|+\xi(\tau))\cdot L\tau.\end{align*} $$
-
Proof of the Claim
The proof is essentially because the map
![]() $\exp ^{-1}_{f(z_0)}\circ f\circ \exp _{z_0}$
is
$\exp ^{-1}_{f(z_0)}\circ f\circ \exp _{z_0}$
is
![]() $C^1$
-smooth at
$C^1$
-smooth at
![]() $0_{z_0}$
and
$0_{z_0}$
and
![]() $D(\exp ^{-1}_{f(z_0)}\circ f\circ \exp _{z_0})(0_{z_0})=Df(z_0)$
. See the details in the proof of [Reference Gan and Shi12, Claim 4.19].
$D(\exp ^{-1}_{f(z_0)}\circ f\circ \exp _{z_0})(0_{z_0})=Df(z_0)$
. See the details in the proof of [Reference Gan and Shi12, Claim 4.19].
3.1.4 The action of
 $\widehat {X}_\tau $
on
$\widehat {X}_\tau $
on
 $\exp ^{-1}_{f(z_0)}(f(q_\tau ))$
$\exp ^{-1}_{f(z_0)}(f(q_\tau ))$
Note first that
This gives
We consider the direct sum
It satisfies that for every
![]() $\tau \in [-\tau ',\tau ']$
:
$\tau \in [-\tau ',\tau ']$
:
-
•
 $\|v_{p_\tau }^{su}\|\leq \|v_{f(q_\tau )}^{su}\|+\sup _{v\in T_{f(z_0)}M(\delta _2)}(\|\widehat {X}_{f(z_0)}^s(v)+\widehat {X}_{f(z_0)}^u(v)\|)\cdot \tau \leq \|v_{f(q_\tau )}^{su}\|+2 a_0 \|\widehat {X}\|\cdot \tau ;$
$\|v_{p_\tau }^{su}\|\leq \|v_{f(q_\tau )}^{su}\|+\sup _{v\in T_{f(z_0)}M(\delta _2)}(\|\widehat {X}_{f(z_0)}^s(v)+\widehat {X}_{f(z_0)}^u(v)\|)\cdot \tau \leq \|v_{f(q_\tau )}^{su}\|+2 a_0 \|\widehat {X}\|\cdot \tau ;$
-
•
 $ v_{p_\tau }^c\geq -\|v_{f(q_\tau )}^c\|+\inf _{v\in T_{f(z_0)}M(\delta _2)}\|\widehat {X}_{f(z_0)}^c(v)\| \cdot \tau \geq -\|v_{f(q_\tau )}^c\|+b_0\cdot \tau .$
$ v_{p_\tau }^c\geq -\|v_{f(q_\tau )}^c\|+\inf _{v\in T_{f(z_0)}M(\delta _2)}\|\widehat {X}_{f(z_0)}^c(v)\| \cdot \tau \geq -\|v_{f(q_\tau )}^c\|+b_0\cdot \tau .$
Combined with Claim 3.2, one has
 $$ \begin{align*}&\|v_{p_\tau}^{su}\|\leq [(\|Df(z_0)\|+\xi(\tau))\cdot L+ 2 a_0 \|\widehat{X}\|)]\cdot\tau \quad\text{and}\\ &\quad v_{p_\tau}^c\geq b_0\cdot \tau -2\eta\cdot(\|Df|_{E^c_{z_0}}\|+\xi(\tau))\cdot L\cdot\tau.\end{align*} $$
$$ \begin{align*}&\|v_{p_\tau}^{su}\|\leq [(\|Df(z_0)\|+\xi(\tau))\cdot L+ 2 a_0 \|\widehat{X}\|)]\cdot\tau \quad\text{and}\\ &\quad v_{p_\tau}^c\geq b_0\cdot \tau -2\eta\cdot(\|Df|_{E^c_{z_0}}\|+\xi(\tau))\cdot L\cdot\tau.\end{align*} $$
3.1.5 The constant
 $\tau _2$
$\tau _2$
By item (1) of Claim 3.2, since
![]() $\xi (\tau )$
is a positive infinitesimal as
$\xi (\tau )$
is a positive infinitesimal as
![]() $\tau \rightarrow 0$
, there exists
$\tau \rightarrow 0$
, there exists
![]() $\tau _2\in (0,\tau ']$
such that for any
$\tau _2\in (0,\tau ']$
such that for any
![]() $\tau \in [-\tau _2,\tau _2]$
, the following holds:
$\tau \in [-\tau _2,\tau _2]$
, the following holds:
Consider the disk
![]() $D^F_{f(z_0)}(\delta ')$
and let
$D^F_{f(z_0)}(\delta ')$
and let
![]() $\varphi ^{su}_{f(z_0)}\colon E^s_{f(z_0)}(\delta _1/2)\oplus E_{f(z_0)}^u(\delta _1/2)\rightarrow E_{f(z_0)}^c(\delta _1/2)$
be the
$\varphi ^{su}_{f(z_0)}\colon E^s_{f(z_0)}(\delta _1/2)\oplus E_{f(z_0)}^u(\delta _1/2)\rightarrow E_{f(z_0)}^c(\delta _1/2)$
be the
![]() $C^r$
-map whose graph determines
$C^r$
-map whose graph determines
![]() $D^F_{f(z_0)}(\delta ')$
through the exponential map
$D^F_{f(z_0)}(\delta ')$
through the exponential map
![]() $\exp _{f(z_0)}$
. When
$\exp _{f(z_0)}$
. When
![]() $\tau \in (0,\tau _2]$
, by the choice of
$\tau \in (0,\tau _2]$
, by the choice of
![]() $\eta $
, one has
$\eta $
, one has
 $$ \begin{align*} v_{p_\tau}^c- \varphi^{su}_{f(z_0)}(v_{p_\tau}^{su}) &>b_0\cdot \tau -2\eta\cdot(\|Df|_{E^c_{z_0}}\|+1)\cdot L\cdot\tau- 2\eta\|v_{p_\tau}^{su}\|\\ &> b_0\cdot \tau - 2\eta\cdot [2(\|Df\|+1)\cdot L+ 2 a_0\|\widehat{X}\| ]\cdot\tau\\ &>b_0\cdot \tau - \frac{b_0}{2}\cdot \tau =\frac{b_0}{2}\cdot \tau. \end{align*} $$
$$ \begin{align*} v_{p_\tau}^c- \varphi^{su}_{f(z_0)}(v_{p_\tau}^{su}) &>b_0\cdot \tau -2\eta\cdot(\|Df|_{E^c_{z_0}}\|+1)\cdot L\cdot\tau- 2\eta\|v_{p_\tau}^{su}\|\\ &> b_0\cdot \tau - 2\eta\cdot [2(\|Df\|+1)\cdot L+ 2 a_0\|\widehat{X}\| ]\cdot\tau\\ &>b_0\cdot \tau - \frac{b_0}{2}\cdot \tau =\frac{b_0}{2}\cdot \tau. \end{align*} $$
Thus, when
![]() $0<\tau <\tau _2$
, the point
$0<\tau <\tau _2$
, the point
belongs to
![]() $D^{F}_{\theta _{i+1}(t)}(\delta ')$
for some
$D^{F}_{\theta _{i+1}(t)}(\delta ')$
for some
![]() $t'\in \mathbb {R}_{i+1}$
that satisfies
$t'\in \mathbb {R}_{i+1}$
that satisfies
Finally, consider the segment
One has that
![]() $\gamma $
is tangent to the
$\gamma $
is tangent to the
![]() $\eta _0$
-cone field of
$\eta _0$
-cone field of
![]() $E^c$
with length uniformly bounded from from below (depending on
$E^c$
with length uniformly bounded from from below (depending on
![]() $\tau $
). By item (3) of §2.4.1, there exists
$\tau $
). By item (3) of §2.4.1, there exists
![]() $\Delta _\tau>0$
such that
$\Delta _\tau>0$
such that
![]() $t'-\theta ^*f(t)>\Delta _\tau $
. As a consequence, one has
$t'-\theta ^*f(t)>\Delta _\tau $
. As a consequence, one has
This completes the proof.
Remark 3.3. The constant
![]() $\Delta _\tau $
depends on
$\Delta _\tau $
depends on
![]() $f,X,F$
, and
$f,X,F$
, and
![]() $\tau $
but is independent of the choice of center pseudo orbit
$\tau $
but is independent of the choice of center pseudo orbit
![]() $\Gamma $
.
$\Gamma $
.
3.2 Proof of Theorem A
Based on Proposition 3.1, we are ready to prove Theorem A. As we have mentioned before, we have to deal with general orbits of center leaves rather than periodic ones which are considered in the proof of [Reference Gan and Shi12, Theorem 2.3].
Proof of Theorem A
Let
![]() $f\in \operatorname {DPH}_1^r(M), r\in \mathbb {N}_{\geq 2}$
. Assume
$f\in \operatorname {DPH}_1^r(M), r\in \mathbb {N}_{\geq 2}$
. Assume
![]() $X\in \mathcal {X}^r(M)$
is a vector field that is transverse to
$X\in \mathcal {X}^r(M)$
is a vector field that is transverse to
![]() $E^s\oplus E^u$
and the constant
$E^s\oplus E^u$
and the constant
![]() $\varepsilon _0$
is taken as in §2.1. Let
$\varepsilon _0$
is taken as in §2.1. Let
![]() $L>1$
be from Theorem 2.10. Let the constant
$L>1$
be from Theorem 2.10. Let the constant
![]() $\eta>0$
, the
$\eta>0$
, the
![]() $C^\infty $
-bundle
$C^\infty $
-bundle
![]() $F\subset TM$
, and the constant
$F\subset TM$
, and the constant
![]() $\tau _2$
be from Proposition 3.1. For each
$\tau _2$
be from Proposition 3.1. For each
 $$ \begin{align*}k>2\max\bigg\{\frac{1}{\tau_2},\frac{L+1}{\varepsilon_0}\bigg\},\end{align*} $$
$$ \begin{align*}k>2\max\bigg\{\frac{1}{\tau_2},\frac{L+1}{\varepsilon_0}\bigg\},\end{align*} $$
let
![]() $\Delta _{1/k}>0$
be the constant associated to
$\Delta _{1/k}>0$
be the constant associated to
![]() $\tau =1/k$
from Proposition 3.1 and take
$\tau =1/k$
from Proposition 3.1 and take
![]() $\varepsilon \in (0,\varepsilon _0)$
satisfying
$\varepsilon \in (0,\varepsilon _0)$
satisfying
Assume
![]() $x\dashv _f y$
. By Proposition 2.1, one takes an
$x\dashv _f y$
. By Proposition 2.1, one takes an
![]() $\varepsilon $
-center pseudo orbit
$\varepsilon $
-center pseudo orbit
such that
Moreover, one assumes that
![]() $\Gamma $
satisfies Lemma 2.5. Additionally, if
$\Gamma $
satisfies Lemma 2.5. Additionally, if
![]() $x\in \operatorname {CR}(f)$
, that is,
$x\in \operatorname {CR}(f)$
, that is,
![]() $y=x$
, one can take
$y=x$
, one can take
![]() $\Gamma $
to satisfy that
$\Gamma $
to satisfy that
![]() $x_0=x_n$
by Proposition 2.1 and Remark 2.2. Without loss of generality, we assume that
$x_0=x_n$
by Proposition 2.1 and Remark 2.2. Without loss of generality, we assume that
![]() $-\varepsilon <t_i\leq 0$
for each
$-\varepsilon <t_i\leq 0$
for each
![]() $0\leq i\leq n$
and the other case is symmetric.
$0\leq i\leq n$
and the other case is symmetric.
Let
![]() $\Gamma _\infty =\{x_i\}_{i=-\infty }^{+\infty }$
be the extended bi-infinite center pseudo orbit such that
$\Gamma _\infty =\{x_i\}_{i=-\infty }^{+\infty }$
be the extended bi-infinite center pseudo orbit such that
![]() $x_i=f^i(x_0)$
when
$x_i=f^i(x_0)$
when
![]() $i\leq -1$
and
$i\leq -1$
and
![]() $x_i=f^{i-n}(x_n)$
when
$x_i=f^{i-n}(x_n)$
when
![]() $i\geq n+1$
. Denote by
$i\geq n+1$
. Denote by
the bundle dynamics associated to
![]() $\Gamma _\infty $
as in §2.3. Moreover, let
$\Gamma _\infty $
as in §2.3. Moreover, let
be the action of lifting vector field of X composed with
![]() $\theta ^*f$
as in §2.4.
$\theta ^*f$
as in §2.4.
From the choice of center pseudo orbit
![]() $\Gamma $
, one knows that
$\Gamma $
, one knows that
In the trivial case when
![]() $\widetilde f_0^n(0_0)=0_n$
, which is equivalent to
$\widetilde f_0^n(0_0)=0_n$
, which is equivalent to
![]() $f^n(x_0)=x_n$
, the collection
$f^n(x_0)=x_n$
, the collection
![]() $\{x_0,x_1,\ldots ,x_n\}$
is a piece of orbit segment from
$\{x_0,x_1,\ldots ,x_n\}$
is a piece of orbit segment from
![]() $x_0$
to
$x_0$
to
![]() $x_n$
and the conclusion holds automatically.
$x_n$
and the conclusion holds automatically.
We now assume that
![]() $\widetilde f_0^n(0_0)<0_n$
. Consider the bundle dynamics
$\widetilde f_0^n(0_0)<0_n$
. Consider the bundle dynamics
![]() $\theta ^*f$
on the lifting bundle
$\theta ^*f$
on the lifting bundle
![]() $\theta ^*(F^s\oplus F^u)$
and its perturbation
$\theta ^*(F^s\oplus F^u)$
and its perturbation
![]() $\widetilde f_{1/k}=\widetilde {X}_{1/k}\circ \theta ^*f$
defined on
$\widetilde f_{1/k}=\widetilde {X}_{1/k}\circ \theta ^*f$
defined on
![]() $\theta ^*(F^s\oplus F^u)(\delta _0/C_0)$
. Let
$\theta ^*(F^s\oplus F^u)(\delta _0/C_0)$
. Let
![]() $h_{1/k}\colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \bigsqcup \nolimits _{i\in \mathbb {Z}}\sigma _{1/k}(\mathbb {R}_i)$
be the leaf conjugacy in §2.4.1. Note that by the choices of constants, one has
$h_{1/k}\colon \bigsqcup \nolimits _{i\in \mathbb {Z}}\mathbb {R}_i\rightarrow \bigsqcup \nolimits _{i\in \mathbb {Z}}\sigma _{1/k}(\mathbb {R}_i)$
be the leaf conjugacy in §2.4.1. Note that by the choices of constants, one has
By Proposition 3.1, one has the following estimation for the zero point
![]() $0_0\in \mathbb {R}_0$
:
$0_0\in \mathbb {R}_0$
:
 $$ \begin{align*} \widetilde{f}_{1/k}^n(h_{1/k}(0_0)) &> \widetilde{f}_{1/k}^{n-1}(h_{1/k}(\theta^*f(0_0)+\Delta_{1/k})) = \widetilde{f}_{1/k}^{n-1}(h_{1/k}(t_1+\Delta_{1/k}))\\ &> \widetilde{f}_{1/k}^{n-1}(h_{1/k}(0_1))\\ &>\cdots\cdots \\ &> \widetilde{f}_{1/k}(h_{1/k}(0_{n-1}))\\ &> h_{1/k}(\theta^*f(0_{n-1})+\Delta_{1/k})= h_{1/k}(t_n+\Delta_{1/k})\\ &> h_{1/k}(0_n). \end{align*} $$
$$ \begin{align*} \widetilde{f}_{1/k}^n(h_{1/k}(0_0)) &> \widetilde{f}_{1/k}^{n-1}(h_{1/k}(\theta^*f(0_0)+\Delta_{1/k})) = \widetilde{f}_{1/k}^{n-1}(h_{1/k}(t_1+\Delta_{1/k}))\\ &> \widetilde{f}_{1/k}^{n-1}(h_{1/k}(0_1))\\ &>\cdots\cdots \\ &> \widetilde{f}_{1/k}(h_{1/k}(0_{n-1}))\\ &> h_{1/k}(\theta^*f(0_{n-1})+\Delta_{1/k})= h_{1/k}(t_n+\Delta_{1/k})\\ &> h_{1/k}(0_n). \end{align*} $$
Recall that
![]() $\widetilde f_0^n(0_0)<0_n$
and
$\widetilde f_0^n(0_0)<0_n$
and
![]() $\sigma _{\tau }$
as well as
$\sigma _{\tau }$
as well as
![]() $h_\tau $
varies continuously with respect to
$h_\tau $
varies continuously with respect to
![]() $\tau $
. Thus, there exists
$\tau $
. Thus, there exists
![]() $\tau _k\in (0,1/k)$
such that
$\tau _k\in (0,1/k)$
such that
Let
![]() $p_k=\Phi (h_{\tau _k}(0_0))$
and
$p_k=\Phi (h_{\tau _k}(0_0))$
and
![]() $q_k=\Phi (h_{\tau _k}(0_n))$
, then it satisfies
$q_k=\Phi (h_{\tau _k}(0_n))$
, then it satisfies
Moreover, by Theorem 2.10, one has that
In particular, when
![]() $x\in \operatorname {CR}(f)$
, that is,
$x\in \operatorname {CR}(f)$
, that is,
![]() $y=x$
, one has
$y=x$
, one has
![]() $x_0=x_n$
as well as
$x_0=x_n$
as well as
![]() $0_0=0_n$
, which implies that
$0_0=0_n$
, which implies that
As a consequence, one has that
![]() $f_{\tau _k}^n(p_k)=(X_{\tau _k}\circ f)^n(p_k)=p_k.$
$f_{\tau _k}^n(p_k)=(X_{\tau _k}\circ f)^n(p_k)=p_k.$
By taking
![]() $k\rightarrow \infty $
, this allows
$k\rightarrow \infty $
, this allows
![]() $\varepsilon $
to be arbitrarily small for the
$\varepsilon $
to be arbitrarily small for the
![]() $\varepsilon $
-center pseudo orbit
$\varepsilon $
-center pseudo orbit
![]() $\Gamma $
. This finishes the proof of Theorem A.
$\Gamma $
. This finishes the proof of Theorem A.
3.3 Proof of Corollary B
Based on Theorem A, the proof of item (1) in Corollary B is obtained from the classical Baire arguments, see for instance [Reference Bonatti and Crovisier4, §5] and [Reference Gan and Wen13, §3]. Items (2) and (3) are direct consequences of item (1). We provide a short proof for completeness of the paper. As we have mentioned, the reason that we consider the set
![]() $\operatorname {DEPH}^r_1(M)$
in Corollary B is because
$\operatorname {DEPH}^r_1(M)$
in Corollary B is because
![]() $\operatorname {DEPH}^r_1(M)$
forms an open set in
$\operatorname {DEPH}^r_1(M)$
forms an open set in
![]() $\operatorname {PH}^r(M)$
.
$\operatorname {PH}^r(M)$
.
Proof of Corollary B
As a consequence of [Reference Gan and Shi12, Theorem A], there exists a dense
![]() $G_\delta $
subset
$G_\delta $
subset
![]() $\mathcal {R}_0$
in
$\mathcal {R}_0$
in
![]() $\operatorname {DEPH}_1^r(M)$
such that every
$\operatorname {DEPH}_1^r(M)$
such that every
![]() $f\in \mathcal {R}_0$
satisfies
$f\in \mathcal {R}_0$
satisfies
![]() $\Omega (f)=\overline {\mathrm {Per}(f)}$
.
$\Omega (f)=\overline {\mathrm {Per}(f)}$
.
Take a countable basis
![]() $\{O_n\}_{n\in \mathbb {N}}$
of M and let
$\{O_n\}_{n\in \mathbb {N}}$
of M and let
![]() $\{W_n\}_{n\in \mathbb {N}}$
be the countable collection where every
$\{W_n\}_{n\in \mathbb {N}}$
be the countable collection where every
![]() $W_n$
is the union of finitely many elements in
$W_n$
is the union of finitely many elements in
![]() $\{O_n\}_{n\in \mathbb {N}}$
. For each
$\{O_n\}_{n\in \mathbb {N}}$
. For each
![]() $n,m\in \mathbb {N}$
, one defines the following two open sets
$n,m\in \mathbb {N}$
, one defines the following two open sets
![]() $\mathcal {H}_{n,m}$
and
$\mathcal {H}_{n,m}$
and
![]() $\mathcal {N}_{n,m}$
in
$\mathcal {N}_{n,m}$
in
![]() $\operatorname {DEPH}_1^r(M)$
:
$\operatorname {DEPH}_1^r(M)$
:
-
•
 $f\in \mathcal {H}_{n,m}$
if there exists a neighborhood
$f\in \mathcal {H}_{n,m}$
if there exists a neighborhood
 $\mathcal {U}$
of f in
$\mathcal {U}$
of f in
 $\operatorname {DEPH}_1^r(M)$
such that for any
$\operatorname {DEPH}_1^r(M)$
such that for any
 $g\in \mathcal {U}$
, there exists
$g\in \mathcal {U}$
, there exists
 $k\geq 1$
satisfying
$k\geq 1$
satisfying
 $g^k(W_n)\cap W_m\neq \emptyset $
;
$g^k(W_n)\cap W_m\neq \emptyset $
; -
•
 $f\in \mathcal {N}_{n,m}$
if there exists a neighborhood
$f\in \mathcal {N}_{n,m}$
if there exists a neighborhood
 $\mathcal {U}$
of f in
$\mathcal {U}$
of f in
 $\operatorname {DEPH}_1^r(M)$
such that for any
$\operatorname {DEPH}_1^r(M)$
such that for any
 $g\in \mathcal {U}$
and for any
$g\in \mathcal {U}$
and for any
 $k\geq 1$
, it satisfies
$k\geq 1$
, it satisfies
 $g^k(W_n)\cap W_m=\emptyset $
.
$g^k(W_n)\cap W_m=\emptyset $
.
It is not difficult to verify that
![]() $\mathcal {N}_{n,m}=\mathrm {Int} (\operatorname {DEPH}_1^r(M)\setminus \mathcal {H}_{n,m})$
, where
$\mathcal {N}_{n,m}=\mathrm {Int} (\operatorname {DEPH}_1^r(M)\setminus \mathcal {H}_{n,m})$
, where
![]() $\mathrm {Int}(\cdot )$
means taking the interior. Thus,
$\mathrm {Int}(\cdot )$
means taking the interior. Thus,
![]() $\mathcal {H}_{n,m}\cup \mathcal {N}_{n,m}$
is open dense in
$\mathcal {H}_{n,m}\cup \mathcal {N}_{n,m}$
is open dense in
![]() $\operatorname {DEPH}_1^r(M)$
. Let
$\operatorname {DEPH}_1^r(M)$
. Let
 $$ \begin{align*}\mathcal{R}=\mathcal{R}_0\cap \bigg(\bigcap_{n,m\in\mathbb{N}}(\mathcal{H}_{n,m}\cup \mathcal{N}_{n,m})\bigg).\end{align*} $$
$$ \begin{align*}\mathcal{R}=\mathcal{R}_0\cap \bigg(\bigcap_{n,m\in\mathbb{N}}(\mathcal{H}_{n,m}\cup \mathcal{N}_{n,m})\bigg).\end{align*} $$
Then
![]() $\mathcal {R}$
is a dense
$\mathcal {R}$
is a dense
![]() $G_\delta $
subset in
$G_\delta $
subset in
![]() $\operatorname {DEPH}_1^r(M)$
. We claim that the conclusions of Corollary B hold for
$\operatorname {DEPH}_1^r(M)$
. We claim that the conclusions of Corollary B hold for
![]() $f\in \mathcal {R}$
.
$f\in \mathcal {R}$
.
Let
![]() $f\in \mathcal {R}$
. Assume
$f\in \mathcal {R}$
. Assume
![]() $x\dashv _f y$
. For any neighborhood U of x and any neighborhood V of y, take
$x\dashv _f y$
. For any neighborhood U of x and any neighborhood V of y, take
![]() $n,m\in \mathbb {N}$
such that
$n,m\in \mathbb {N}$
such that
![]() $W_n\subset U$
and
$W_n\subset U$
and
![]() $W_m\subset V$
. By Theorem A, for any neighborhood
$W_m\subset V$
. By Theorem A, for any neighborhood
![]() $\mathcal {U}$
of f in
$\mathcal {U}$
of f in
![]() $\operatorname {DEPH}_1^r(M)$
, there exists
$\operatorname {DEPH}_1^r(M)$
, there exists
![]() $g\in \mathcal {U}$
and
$g\in \mathcal {U}$
and
![]() $k\geq 1$
such that
$k\geq 1$
such that
![]() $g^k(W_n)\cap W_m\neq \emptyset $
. This implies that
$g^k(W_n)\cap W_m\neq \emptyset $
. This implies that
![]() $f\in \mathcal {H}_{n,m}$
since
$f\in \mathcal {H}_{n,m}$
since
![]() $f\in \mathcal {H}_{n,m}\cup \mathcal {N}_{n,m}$
. As a consequence, there exists
$f\in \mathcal {H}_{n,m}\cup \mathcal {N}_{n,m}$
. As a consequence, there exists
![]() $\ell>1$
such that
$\ell>1$
such that
![]() $f^\ell (U)\cap V\neq \emptyset $
by the definition of
$f^\ell (U)\cap V\neq \emptyset $
by the definition of
![]() $\mathcal {H}_{n,m}$
together with the fact
$\mathcal {H}_{n,m}$
together with the fact
![]() $W_n\subset U$
and
$W_n\subset U$
and
![]() $W_m\subset V$
. Since U and V are taken arbitrarily, one has
$W_m\subset V$
. Since U and V are taken arbitrarily, one has
![]() $x\prec _f y$
. This proves item (1).
$x\prec _f y$
. This proves item (1).
By item (1), for any
![]() $x\in \operatorname {CR}(f)$
, it satisfies
$x\in \operatorname {CR}(f)$
, it satisfies
![]() $x\prec _f x$
which is equivalent to say
$x\prec _f x$
which is equivalent to say
![]() $x\in \Omega (f)$
. Thus, one has
$x\in \Omega (f)$
. Thus, one has
![]() $\operatorname {CR}(f)=\Omega (f)$
. Since
$\operatorname {CR}(f)=\Omega (f)$
. Since
![]() $f\in \mathcal {R}$
, one has
$f\in \mathcal {R}$
, one has
![]() $\Omega (f)=\overline {\mathrm {Per}(f)}$
, This verifies item (2).
$\Omega (f)=\overline {\mathrm {Per}(f)}$
, This verifies item (2).
To prove item (3), assume
![]() $f\in \mathcal {R}$
is chain-transitive. For any two non-empty open sets
$f\in \mathcal {R}$
is chain-transitive. For any two non-empty open sets
![]() $U,V\subset M$
, there exists
$U,V\subset M$
, there exists
![]() $x\in U$
and
$x\in U$
and
![]() $y\in V$
such that
$y\in V$
such that
![]() $x\dashv _f y$
. By item (1), one has
$x\dashv _f y$
. By item (1), one has
![]() $x\prec _f y$
, thus there exists
$x\prec _f y$
, thus there exists
![]() $n\geq 1$
such that
$n\geq 1$
such that
![]() $f^n(U)\cap V\neq \emptyset $
. This proves that f is transitive.
$f^n(U)\cap V\neq \emptyset $
. This proves that f is transitive.
Acknowledgments
We are very grateful to the anonymous referees for their valuable suggestions. Y.S. was partially supported by National Key R&D Program of China (2020YFE0204200, 2021YFA1001900), NSFC (12071007, 11831001, 12090015) and the Fundamental Research Funds for the Central Universities. X.W. was partially supported by National Key R&D Program of China (2021YFA1001900), NSFC (12071285) and Innovation Program of Shanghai Municipal Education Commission (No. 2021-01-07-00-02-E00087).