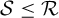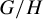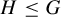1. Introduction
Let
![]() $\Gamma $
be an infinite group generated by a finite symmetric set S and let
$\Gamma $
be an infinite group generated by a finite symmetric set S and let
![]() $G=\mathrm {Cay}(\Gamma ,S)$
be its Cayley graph. We would like to measure the size of certain subsets C of
$G=\mathrm {Cay}(\Gamma ,S)$
be its Cayley graph. We would like to measure the size of certain subsets C of
![]() $\Gamma $
, in a translation-invariant way, using the graph structure of G. As a measuring tool, we will use the lazy (laziness is convenient, but it is not necessary; see §3.3 for details) random walk
$\Gamma $
, in a translation-invariant way, using the graph structure of G. As a measuring tool, we will use the lazy (laziness is convenient, but it is not necessary; see §3.3 for details) random walk
![]() $(g_n)$
on G, starting at the identity, through the sampling probabilities
$(g_n)$
on G, starting at the identity, through the sampling probabilities
We are mostly interested in the case when C has zero density and consider the sampling exponent
When H is a subgroup of
![]() $\Gamma $
, the limit defining
$\Gamma $
, the limit defining
![]() $\rho (H)$
will exist and be equal to the spectral radius of the random walk on the quotient Schreier graph
$\rho (H)$
will exist and be equal to the spectral radius of the random walk on the quotient Schreier graph
![]() $\mathrm {Sch}(\Gamma ,H,S)$
. Indeed, the covering map
$\mathrm {Sch}(\Gamma ,H,S)$
. Indeed, the covering map
![]() $\Gamma \rightarrow \Gamma /H$
gives a bijection between walks returning to H on
$\Gamma \rightarrow \Gamma /H$
gives a bijection between walks returning to H on
![]() $\Gamma $
and walks returning to the root on
$\Gamma $
and walks returning to the root on
![]() $\mathrm {Sch} (\Gamma ,H,S)$
. There is a considerable literature on this notion [Reference Bartholdi and Virág7, Reference Kaimanovich and Woess28, Reference Soardi and Woess36, Reference Woess39, Reference Żuk40], starting with the amenability criterion of Kesten [Reference Abért, Glasner and Virág3, Reference Abért, Glasner and Virág4, Reference Kesten30]. For arbitrary subsets of
$\mathrm {Sch} (\Gamma ,H,S)$
. There is a considerable literature on this notion [Reference Bartholdi and Virág7, Reference Kaimanovich and Woess28, Reference Soardi and Woess36, Reference Woess39, Reference Żuk40], starting with the amenability criterion of Kesten [Reference Abért, Glasner and Virág3, Reference Abért, Glasner and Virág4, Reference Kesten30]. For arbitrary subsets of
![]() $\Gamma $
, the sampling exponent will not exist in general, but the picture changes when it is defined by a
$\Gamma $
, the sampling exponent will not exist in general, but the picture changes when it is defined by a
![]() $\Gamma $
-invariant stochastic process. The most studied such subsets [Reference Benjamini and Schramm9, Reference Hutchcroft21, Reference Hutchcroft22, Reference Lyons and Peres33–Reference Pak and Smirnova-Nagnibeda35] are percolation clusters of an independent and identically distributed (i.i.d.) (site or bond) percolation on Cayley graphs.
$\Gamma $
-invariant stochastic process. The most studied such subsets [Reference Benjamini and Schramm9, Reference Hutchcroft21, Reference Hutchcroft22, Reference Lyons and Peres33–Reference Pak and Smirnova-Nagnibeda35] are percolation clusters of an independent and identically distributed (i.i.d.) (site or bond) percolation on Cayley graphs.
Theorem 1.1. Let
![]() $\Gamma $
be a countable group and consider an i.i.d. percolation on a Cayley graph of
$\Gamma $
be a countable group and consider an i.i.d. percolation on a Cayley graph of
![]() $\Gamma $
. Then almost surely, for every connected component C of the percolation, the limit
$\Gamma $
. Then almost surely, for every connected component C of the percolation, the limit
exists.
This result is most interesting when the percolation clusters are infinite and there are infinitely many of them almost surely. It is easy to see that once
![]() $\rho (C)$
exists, it is independent of the starting point of the walk and so, by the indistinguishability theorem of Lyons and Schramm [Reference Lyons and Schramm34, Theorem 3.3], it will be a constant on infinite clusters, depending only on the percolation parameter. Note that when
$\rho (C)$
exists, it is independent of the starting point of the walk and so, by the indistinguishability theorem of Lyons and Schramm [Reference Lyons and Schramm34, Theorem 3.3], it will be a constant on infinite clusters, depending only on the percolation parameter. Note that when
![]() $\Gamma $
is amenable, the above phase does not exist for i.i.d. percolations, but by Kesten’s theorem [Reference Kesten30], in this case,
$\Gamma $
is amenable, the above phase does not exist for i.i.d. percolations, but by Kesten’s theorem [Reference Kesten30], in this case,
![]() $\rho (C)$
equals
$\rho (C)$
equals
![]() $1$
for any subset C anyway. That is,
$1$
for any subset C anyway. That is,
![]() $\rho $
is not a suitable measuring tool for amenable groups. For non-amenable groups, it is a well-known conjecture that the non-uniqueness phase exists for any Cayley graph of the group [Reference Benjamini and Schramm9].
$\rho $
is not a suitable measuring tool for amenable groups. For non-amenable groups, it is a well-known conjecture that the non-uniqueness phase exists for any Cayley graph of the group [Reference Benjamini and Schramm9].
We establish the above theorem in a much wider generality, using the framework of countable-measure-preserving equivalence relations. Note that our most general results in this direction (see Theorem 3.2, as well as §5 for the translation between relations and percolation) do not even involve an ambient group anymore, but for this introduction we stick to group actions.
Let
![]() $(X,\mu )$
be a standard Borel probability space and let
$(X,\mu )$
be a standard Borel probability space and let
![]() $\Gamma $
act on
$\Gamma $
act on
![]() $(X,\mu )$
by
$(X,\mu )$
by
![]() $\mu $
-preserving maps. We define the orbit relation
$\mu $
-preserving maps. We define the orbit relation
A subrelation S of
![]() ${\mathcal R}$
is a Borel subset of
${\mathcal R}$
is a Borel subset of
![]() ${\mathcal R}$
that, as a relation on X, is an equivalence relation. Orbit relations and their subrelations are commonly studied objects in measured group theory; see [Reference Furman16–Reference Gaboriau, Bhatia, Pal, Rangarajan, Srinivas and Vanninathan20, Reference Kechris and Miller29].
${\mathcal R}$
that, as a relation on X, is an equivalence relation. Orbit relations and their subrelations are commonly studied objects in measured group theory; see [Reference Furman16–Reference Gaboriau, Bhatia, Pal, Rangarajan, Srinivas and Vanninathan20, Reference Kechris and Miller29].
Let
![]() ${\mathcal S}$
be a subrelation of
${\mathcal S}$
be a subrelation of
![]() ${\mathcal R}$
. For
${\mathcal R}$
. For
![]() $x,y\in X$
such that
$x,y\in X$
such that
![]() $(x,y)\in {\mathcal R}$
and for a natural n, let the sampling probabilities be
$(x,y)\in {\mathcal R}$
and for a natural n, let the sampling probabilities be
where, as before,
![]() $(g_{n})$
is the lazy random walk on G starting at the identity of
$(g_{n})$
is the lazy random walk on G starting at the identity of
![]() $\Gamma $
. That is, we walk from x and take the probability that we hit the
$\Gamma $
. That is, we walk from x and take the probability that we hit the
![]() ${\mathcal S}$
-class of y.
${\mathcal S}$
-class of y.
Theorem 1.2. Let
![]() $\Gamma $
be a countable group acting by measure-preserving maps on
$\Gamma $
be a countable group acting by measure-preserving maps on
![]() $(X,\mu )$
and let
$(X,\mu )$
and let
![]() ${\mathcal S}$
be a subrelation of the orbit relation of the action. Then for
${\mathcal S}$
be a subrelation of the orbit relation of the action. Then for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $y\in X$
, for every
$y\in X$
, for every
![]() $x\in \Gamma y$
,
$x\in \Gamma y$
,
exists and is independent of x. Moreover, if
![]() ${\mathcal S}$
is either normal or ergodic, then
${\mathcal S}$
is either normal or ergodic, then
![]() $\rho ^{{\mathcal S}}$
is almost surely constant.
$\rho ^{{\mathcal S}}$
is almost surely constant.
Note that one can also state an equivalent stochastic form of Theorem 1.2 using the notion of an invariant random partition, that is, a random partition of the group that is invariant in distribution under the shift action. Invariant random partitions are defined in [Reference Tucker-Drob38, §8.1]. They are natural stochastic generalizations of subgroups, as individually shift-invariant partitions are exactly coset partitions with respect to a subgroup. The reformulation says that for any invariant random partition of a countable group, all the partition classes have well-defined sampling exponents. We chose to state Theorem 1.2 in the language of relations because that is the internal language of its proof. We develop the language of invariant random partitions in the paper [Reference Abert, Fraczyk and Hayes2].
Theorem 1.2 does not seem to follow from the usual arguments. The local environment may look quite different from different points of a class. In algebraic terms, there is no natural quotient object on which the group would act. This is a major deviation from the subgroup case, where this homogeneity holds and trivially makes
![]() $p_{n,H}$
supermultiplicative in n. As a result, we were not able to derive the existence of the sampling exponent with the usual tools, including the standard or Kingman ergodic theorems. For the case of unimodular random trees, Theorem 1.1 follows from an argument we call the
$p_{n,H}$
supermultiplicative in n. As a result, we were not able to derive the existence of the sampling exponent with the usual tools, including the standard or Kingman ergodic theorems. For the case of unimodular random trees, Theorem 1.1 follows from an argument we call the
![]() $2$
–
$2$
–
![]() $3$
method. In order to prove Theorem 1.2 we introduce a generalized version of
$3$
method. In order to prove Theorem 1.2 we introduce a generalized version of
![]() $2$
–
$2$
–
![]() $3$
method, which we expect to have more applications. We recall the rough idea behind the
$3$
method, which we expect to have more applications. We recall the rough idea behind the
![]() $2$
–
$2$
–
![]() $3$
method is to establish a local submultiplicative nature of the sequence and then yield the existence of the limit by a density argument. The reader can form a quick impression of this method by reading the text after the statement of Theorem 1.5.
$3$
method is to establish a local submultiplicative nature of the sequence and then yield the existence of the limit by a density argument. The reader can form a quick impression of this method by reading the text after the statement of Theorem 1.5.
It turns out that the sampling exponent still admits a spectral interpretation, and equals a norm of a natural Markov-type operator acting on a quotient object of sorts (see Theorem 3.2). Because of that and to keep consistency with the subgroup case, we call the sampling exponent
![]() $\rho ^{S}(x,[y]_{{\mathcal S}})$
the co-spectral radius of the class
$\rho ^{S}(x,[y]_{{\mathcal S}})$
the co-spectral radius of the class
![]() $[y]_{{\mathcal S}}$
in this paper. This operator approach also has interesting connections to prior work in percolation theory. For example, our methods recover a lemma due to Schramm on the connectivity decay of random walks in critical percolation which has been used in later results in percolation theory ([Reference Kozma31], [Reference Hutchcroft21, Lemma 6.4], [Reference Hutchcroft22, §3]). We refer the reader to the discussion preceding §3.2 for more details.
$[y]_{{\mathcal S}}$
in this paper. This operator approach also has interesting connections to prior work in percolation theory. For example, our methods recover a lemma due to Schramm on the connectivity decay of random walks in critical percolation which has been used in later results in percolation theory ([Reference Kozma31], [Reference Hutchcroft21, Lemma 6.4], [Reference Hutchcroft22, §3]). We refer the reader to the discussion preceding §3.2 for more details.
This Markov-type operator is defined on a Hilbert space which is constructed by integrating the bundle of Hilbert spaces
![]() $\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
into one Hilbert space. While we will not need it for this work, this Hilbert space can be naturally related to the basic Jones construction of the inclusion
$\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
into one Hilbert space. While we will not need it for this work, this Hilbert space can be naturally related to the basic Jones construction of the inclusion
![]() $L({\mathcal S})\leq L({\mathcal R})$
of von Neumann algebras of the corresponding equivalence relations, as well as the
$L({\mathcal S})\leq L({\mathcal R})$
of von Neumann algebras of the corresponding equivalence relations, as well as the
![]() $L^{2}$
-space of a natural measure space occurring in [Reference Feldman, Sutherland and Zimmer15] (see Definition 1.4 of that paper). We expect that our new methods will have applications to the operator-algebraic setting. We refer the reader to the discussion preceding §3.1.
$L^{2}$
-space of a natural measure space occurring in [Reference Feldman, Sutherland and Zimmer15] (see Definition 1.4 of that paper). We expect that our new methods will have applications to the operator-algebraic setting. We refer the reader to the discussion preceding §3.1.
We now state the 2–3 method theorem in its most general form that leads to Theorem 1.2.
Theorem 1.3. Let
![]() ${\mathcal R}$
be a discrete, measure-preserving equivalence relation over a standard probability space
${\mathcal R}$
be a discrete, measure-preserving equivalence relation over a standard probability space
![]() $(X,\mu )$
, and fix
$(X,\mu )$
, and fix
![]() $\pi \in L^{1}(X,\mu )$
with
$\pi \in L^{1}(X,\mu )$
with
![]() $\pi (x)\in (0,\infty )$
for almost every
$\pi (x)\in (0,\infty )$
for almost every
![]() $x\in X$
. Let
$x\in X$
. Let
![]() $f_{k}\colon {\mathcal R}\to [0,\infty ]$
for
$f_{k}\colon {\mathcal R}\to [0,\infty ]$
for
![]() $k\geq 1$
be a sequence of measurable functions such that:
$k\geq 1$
be a sequence of measurable functions such that:
-
(a)
 $f_{k}$
is
$f_{k}$
is
 $\pi $
-symmetric for all
$\pi $
-symmetric for all
 $k\in {\mathbb N}$
, that is,
$k\in {\mathbb N}$
, that is,
 $f_{k}(x,y)\pi (y)=f_{k}(y,x)\pi (x)$
for almost every
$f_{k}(x,y)\pi (y)=f_{k}(y,x)\pi (x)$
for almost every
 $(x,y)\in {\mathcal R}$
;
$(x,y)\in {\mathcal R}$
; -
(b) for all
 $l,k\in {\mathbb N}$
we have
$l,k\in {\mathbb N}$
we have
 $\sum _{y,z\in [x]_{{\mathcal R}}}f_{l}(x,z)f_{k}(z,y)\leq \sum _{y\in [x]_{{\mathcal R}}}f_{l+k}(x,y)$
for almost every
$\sum _{y,z\in [x]_{{\mathcal R}}}f_{l}(x,z)f_{k}(z,y)\leq \sum _{y\in [x]_{{\mathcal R}}}f_{l+k}(x,y)$
for almost every
 $x\in X$
;
$x\in X$
; -
(c) for almost every
 $x\in X$
and every
$x\in X$
and every
 $k\in {\mathbb N}$
we have
$k\in {\mathbb N}$
we have
 $0<\sum _{y\in [x]_{{\mathcal R}}}f_{k}(x,y)<\infty $
;
$0<\sum _{y\in [x]_{{\mathcal R}}}f_{k}(x,y)<\infty $
; -
(d) there is a measurable
 $D\colon X\to (0,\infty )$
so that for almost every
$D\colon X\to (0,\infty )$
so that for almost every $$ \begin{align*}\sum_{y\in [x]_{{\mathcal R}}}f_{l+k}(x,y)\geq D(x)^{l}\sum_{y\in [x]_{{\mathcal R}}} f_{k}(x,y)\end{align*} $$
$$ \begin{align*}\sum_{y\in [x]_{{\mathcal R}}}f_{l+k}(x,y)\geq D(x)^{l}\sum_{y\in [x]_{{\mathcal R}}} f_{k}(x,y)\end{align*} $$
 $x\in X$
and every
$x\in X$
and every
 $l,k\in {\mathbb N}$
.
$l,k\in {\mathbb N}$
.
Then
 $$ \begin{align*}\widetilde{f}(x)=\lim_{k\to\infty}\bigg(\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg)^{1/k}\end{align*} $$
$$ \begin{align*}\widetilde{f}(x)=\lim_{k\to\infty}\bigg(\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg)^{1/k}\end{align*} $$
exists and is positive almost surely. Further:
-
(i) for every
 $k\in {\mathbb N}$
,
$k\in {\mathbb N}$
,  $$ \begin{align*}\int\pi(x)\frac{\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)}{\widetilde{f}(x)^{k}}\,d\mu(x)\leq \int \pi\,d\mu;\end{align*} $$
$$ \begin{align*}\int\pi(x)\frac{\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)}{\widetilde{f}(x)^{k}}\,d\mu(x)\leq \int \pi\,d\mu;\end{align*} $$
-
(ii)
 $\lim _{k\to \infty }(\int \pi (x)\sum _{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\,d\mu (x))^{1/k}=\|\widetilde {f}\|_{\infty }.$
$\lim _{k\to \infty }(\int \pi (x)\sum _{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\,d\mu (x))^{1/k}=\|\widetilde {f}\|_{\infty }.$
In the special case when
![]() $f_k(x,y)$
is the probability of transition from x to y by a standard random walk in k steps, the first part of the theorem can be seen as a large-deviations estimate, in the sense that it controls the density of starting points where the random walk sampling probability deviates from what is suggested by the co-spectral radius. In fact, it is natural to ask whether our main result holds in the ‘annealed’ sense, that is, when we take expected value of the sampling probabilities before we take the nth root. A warning comment here is that in this case we have to consider the event of returning to the class of the starting point, because equivalence classes often cannot be individually identified in a measurable way (this is what is called indistinguishability in percolation theory, which is equivalent to the ergodicity of a subrelation in the measured language). In any case, this ‘annealed’ version is much simpler to prove than our main result and most of the effort in this paper is spent establishing the pointwise (or ‘quenched’) version. Additionally, we show that the ‘annealed’ version is the essential supremum of the ‘quenched’ version and that in many cases, the ‘quenched version’ is almost surely constant. See Theorem 3.2 for a precise relation between the ‘annealed’ and ‘quenched’ versions. As a sample application, in the case of Bernoulli bond percolation it follows from the indistinguishability result of Lyons and Schramm [Reference Lyons and Schramm34] and our work that the ‘annealed’ version and the ‘quenched’ version agree on infinite clusters.
$f_k(x,y)$
is the probability of transition from x to y by a standard random walk in k steps, the first part of the theorem can be seen as a large-deviations estimate, in the sense that it controls the density of starting points where the random walk sampling probability deviates from what is suggested by the co-spectral radius. In fact, it is natural to ask whether our main result holds in the ‘annealed’ sense, that is, when we take expected value of the sampling probabilities before we take the nth root. A warning comment here is that in this case we have to consider the event of returning to the class of the starting point, because equivalence classes often cannot be individually identified in a measurable way (this is what is called indistinguishability in percolation theory, which is equivalent to the ergodicity of a subrelation in the measured language). In any case, this ‘annealed’ version is much simpler to prove than our main result and most of the effort in this paper is spent establishing the pointwise (or ‘quenched’) version. Additionally, we show that the ‘annealed’ version is the essential supremum of the ‘quenched’ version and that in many cases, the ‘quenched version’ is almost surely constant. See Theorem 3.2 for a precise relation between the ‘annealed’ and ‘quenched’ versions. As a sample application, in the case of Bernoulli bond percolation it follows from the indistinguishability result of Lyons and Schramm [Reference Lyons and Schramm34] and our work that the ‘annealed’ version and the ‘quenched’ version agree on infinite clusters.
Remark 1.4. The following was pointed out to us by the anonymous referee. As in Theorem 1.1. consider an i.i.d. percolation on the Cayley graph of a group
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $X_{n}$
be a random walk on
$X_{n}$
be a random walk on
![]() $\Gamma $
with
$\Gamma $
with
![]() $X_{0}=e$
and with transition probabilities
$X_{0}=e$
and with transition probabilities
![]() $\mathbb{P} (X_{n}=a|X_{n-1}=b)= \nu (b^{-1}a)$
for some
$\mathbb{P} (X_{n}=a|X_{n-1}=b)= \nu (b^{-1}a)$
for some
![]() $\nu \in \operatorname {Prob}(\Gamma )$
whose support generates
$\nu \in \operatorname {Prob}(\Gamma )$
whose support generates
![]() $\Gamma $
. We let
$\Gamma $
. We let
![]() $\mathbb{P} (X_{0}\leftrightarrow X_{n})$
be the probability that
$\mathbb{P} (X_{0}\leftrightarrow X_{n})$
be the probability that
![]() $X_{n}$
is in the connected component of e in this percolation, and we let C be the connected component of e in this percolation. Theorem 1.3 implies in the context of Theorem 1.1 that
$X_{n}$
is in the connected component of e in this percolation, and we let C be the connected component of e in this percolation. Theorem 1.3 implies in the context of Theorem 1.1 that
almost surely, where C is the cluster of
![]() $X_{0}$
. The subadditive ergodic theorem shows, for example, for Bernoulli percolation that almost surely
$X_{0}$
. The subadditive ergodic theorem shows, for example, for Bernoulli percolation that almost surely
 $$ \begin{align*}\lim_{n\to\infty} \mathbb{P}(X_0 \leftrightarrow X_n | X_n )^{1/n} = \exp \bigg[ \lim_{n\to\infty} \frac{1}{n} {\mathbb E} \log \mathbb{P}(X_0 \leftrightarrow X_n) \bigg].\end{align*} $$
$$ \begin{align*}\lim_{n\to\infty} \mathbb{P}(X_0 \leftrightarrow X_n | X_n )^{1/n} = \exp \bigg[ \lim_{n\to\infty} \frac{1}{n} {\mathbb E} \log \mathbb{P}(X_0 \leftrightarrow X_n) \bigg].\end{align*} $$
So in order to get the correct almost sure decay of the connection probability conditioned on the random walk, one must take the limit of the expectation of the logarithm. Our results says that if one instead conditions on the cluster C, then one does not need to take the expectation of the logarithm. In this sense, our result may be thought of as saying that the major contribution to
![]() ${\mathbb E}[\mathbb{P} (X_{0} \leftrightarrow X_{n}|C)]$
is from contributions which are of ‘typical size’ (up to subexponential factors). For the expectation
${\mathbb E}[\mathbb{P} (X_{0} \leftrightarrow X_{n}|C)]$
is from contributions which are of ‘typical size’ (up to subexponential factors). For the expectation
![]() ${\mathbb E}[\mathbb{P} (X_{0}\leftrightarrow X_{n}|X_{n})]$
this is not the case, and often rare events contribute substantially to the expectation.
${\mathbb E}[\mathbb{P} (X_{0}\leftrightarrow X_{n}|X_{n})]$
this is not the case, and often rare events contribute substantially to the expectation.
1.1. The
 $2$
–
$2$
–
 $3$
method and walk growth
$3$
method and walk growth
We now present another application of the general
![]() $2$
–
$2$
–
![]() $3$
method (see [Reference Abert, Fraczyk and Hayes1, §3] for another application), showing the existence of the exponential rate of growth of the number of walks in any unimodular random rooted graph (see also Example 3.12 in §3.2). We also sketch the proof, as it illustrates quite well what goes into the 2–3 method that is behind Theorem 1.2. Then we state the most general version of the 2–3 method.
$3$
method (see [Reference Abert, Fraczyk and Hayes1, §3] for another application), showing the existence of the exponential rate of growth of the number of walks in any unimodular random rooted graph (see also Example 3.12 in §3.2). We also sketch the proof, as it illustrates quite well what goes into the 2–3 method that is behind Theorem 1.2. Then we state the most general version of the 2–3 method.
Theorem 1.5. Let
![]() $({\mathcal G},o)$
be a connected bounded-degree unimodular random rooted graph with degree at most d. Let
$({\mathcal G},o)$
be a connected bounded-degree unimodular random rooted graph with degree at most d. Let
![]() $w_n(o)$
denote the number of walks of length n starting at o. Then the limit
$w_n(o)$
denote the number of walks of length n starting at o. Then the limit
![]() $\lim _{n\to \infty } ({1}/{n})\log w_n(o)$
exists. Further, if
$\lim _{n\to \infty } ({1}/{n})\log w_n(o)$
exists. Further, if
![]() $({\mathcal G},o)$
is ergodic and
$({\mathcal G},o)$
is ergodic and
![]() $\eta \in \operatorname {Prob}({\mathcal M}_{d})$
is the distribution of
$\eta \in \operatorname {Prob}({\mathcal M}_{d})$
is the distribution of
![]() $({\mathcal G},o)$
, define
$({\mathcal G},o)$
, define
![]() $A\in B(L^{2}({\mathcal M}_{d},\eta ))$
by
$A\in B(L^{2}({\mathcal M}_{d},\eta ))$
by
Then A is a self-adjoint operator and
![]() $\log \|A\|=\lim _{n\to \infty }({1}/{n})\log w_{n}(o).$
$\log \|A\|=\lim _{n\to \infty }({1}/{n})\log w_{n}(o).$
The usual technique used to establish the rate of growth in ergodic theory is the Kingman subadditive theorem. We were not able to find any action or equivalence relation with a submultiplicative cocycle that would control the number of walks in
![]() ${\mathcal G}$
, so we could not use it to solve the problem. As
${\mathcal G}$
, so we could not use it to solve the problem. As
![]() $w_n(o)$
can be naturally expressed as an inner product, one is also tempted to use spectral theory, but this also did not work for us. Instead we use the mass transport principle to show that the inequalities
$w_n(o)$
can be naturally expressed as an inner product, one is also tempted to use spectral theory, but this also did not work for us. Instead we use the mass transport principle to show that the inequalities
hold with overwhelming probability, as n gets large. To see why this is useful, imagine that we know that these inequalities hold always and with the implicit constant
![]() $1$
. Then the sequence
$1$
. Then the sequence
![]() $w_{2^p3^q}(o)$
is submultiplicative, so the limit
$w_{2^p3^q}(o)$
is submultiplicative, so the limit
exists. The function
![]() $n\mapsto \log w_n(o)$
is Lipschitz and the set
$n\mapsto \log w_n(o)$
is Lipschitz and the set
![]() $2^p3^q$
is dense on the logarithmic scale, so we can deduce that the limit
$2^p3^q$
is dense on the logarithmic scale, so we can deduce that the limit
![]() $\lim _{n\to \infty }({1}/{n})\log w_n(o)$
also exists.
$\lim _{n\to \infty }({1}/{n})\log w_n(o)$
also exists.
1.2. Outline of the paper
Section 2 introduces the necessary background for this paper, including a discussion of measure-preserving equivalence relations and how to reduce the study of percolation clusters to equivalence relations. Section 3 contains a proof of the co-spectral radius and its basic properties. In that section we also include some background on representations of equivalence relations, so that in §3.1 we may identify the co-spectral radius with an operator norm. In §3.2 we give a proof of the general
![]() $2$
–
$2$
–
![]() $3$
method which gives us the pointwise existence of the co-spectral radius as a special case. In §3.3 we show that the co-spectral radius is almost surely constant if the subrelation is ergodic or normal. In §4, we show that the co-spectral radius agrees with the spectral radius when the subrelation is hyperfinite and give a counterexample for the converse (i.e., a Kesten theorem for subrelations) using monotone couplings of invariant random subgroups. In §5 we use the co-spectral radius to define new critical exponents for percolation. Finally, in §5.2 we use the
$3$
method which gives us the pointwise existence of the co-spectral radius as a special case. In §3.3 we show that the co-spectral radius is almost surely constant if the subrelation is ergodic or normal. In §4, we show that the co-spectral radius agrees with the spectral radius when the subrelation is hyperfinite and give a counterexample for the converse (i.e., a Kesten theorem for subrelations) using monotone couplings of invariant random subgroups. In §5 we use the co-spectral radius to define new critical exponents for percolation. Finally, in §5.2 we use the
![]() $2$
–
$2$
–
![]() $3$
method to establish the existence of walk growth and relate it to an operator norm.
$3$
method to establish the existence of walk growth and relate it to an operator norm.
Remark. Note that this paper and parts of [Reference Abert, Fraczyk and Hayes1, Reference Abert, Fraczyk and Hayes2] first appeared on arXiv as one long text. Following explicit suggestions of helpful referees, we decided to separate the work into the three papers, making the results more accessible to their natural audiences.
2. Background and notation
A standard probability space is pair
![]() $(X,\mu )$
where X is a standard Borel space, and
$(X,\mu )$
where X is a standard Borel space, and
![]() $\mu $
is the completion of a Borel probability measure on X. We say that
$\mu $
is the completion of a Borel probability measure on X. We say that
![]() $E\subseteq X$
is measurable if it is in the domain of
$E\subseteq X$
is measurable if it is in the domain of
![]() $\mu $
. An equivalence relation over
$\mu $
. An equivalence relation over
![]() $(X,\mu )$
is a Borel subset
$(X,\mu )$
is a Borel subset
![]() ${\mathcal R}\subseteq X\times X$
such that the relation
${\mathcal R}\subseteq X\times X$
such that the relation
![]() $\thicksim $
on X given by
$\thicksim $
on X given by
![]() $x\thicksim y$
if
$x\thicksim y$
if
![]() $(x,y)\in {\mathcal R}$
is an equivalence relation. For
$(x,y)\in {\mathcal R}$
is an equivalence relation. For
![]() $x\in X$
, we let
$x\in X$
, we let
![]() $[x]_{{\mathcal R}}=\{y\in X:(x,y)\in {\mathcal R}$
. We say that
$[x]_{{\mathcal R}}=\{y\in X:(x,y)\in {\mathcal R}$
. We say that
![]() ${\mathcal R}$
is discrete if for almost every
${\mathcal R}$
is discrete if for almost every
![]() $x\in X$
we have that
$x\in X$
we have that
![]() $[x]_{{\mathcal R}}$
is countable. If
$[x]_{{\mathcal R}}$
is countable. If
![]() ${\mathcal R}$
is discrete, we may turn
${\mathcal R}$
is discrete, we may turn
![]() ${\mathcal R}$
into a
${\mathcal R}$
into a
![]() $\sigma $
-finite measure space by endowing
$\sigma $
-finite measure space by endowing
![]() ${\mathcal R}$
with the Borel measure
${\mathcal R}$
with the Borel measure
We will continue to use
![]() $\overline {\mu }$
for the completion of
$\overline {\mu }$
for the completion of
![]() $\overline {\mu }$
. If
$\overline {\mu }$
. If
![]() ${\mathcal R}$
is discrete, we say that it is measure-preserving if the map
${\mathcal R}$
is discrete, we say that it is measure-preserving if the map
![]() ${\mathcal R}\to {\mathcal R}$
given by
${\mathcal R}\to {\mathcal R}$
given by
![]() $(x,y)\mapsto (y,x)$
is measure-preserving. Equivalently, this just means that the mass-transport principle holds: if
$(x,y)\mapsto (y,x)$
is measure-preserving. Equivalently, this just means that the mass-transport principle holds: if
![]() $f\colon {\mathcal R}\to [0,\infty ]$
is Borel, then
$f\colon {\mathcal R}\to [0,\infty ]$
is Borel, then
 $$ \begin{align*}\int_{X}\sum_{y\in [x]_{{\mathcal R}}}f(x,y)\,d\mu(x)=\int_{X}\sum_{y\in [x]_{{\mathcal R}}}f(y,x)\,d\mu(x).\end{align*} $$
$$ \begin{align*}\int_{X}\sum_{y\in [x]_{{\mathcal R}}}f(x,y)\,d\mu(x)=\int_{X}\sum_{y\in [x]_{{\mathcal R}}}f(y,x)\,d\mu(x).\end{align*} $$
For a group
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $S\subseteq \Gamma $
, we use
$S\subseteq \Gamma $
, we use
![]() $\langle S \rangle $
for the subgroup of
$\langle S \rangle $
for the subgroup of
![]() $\Gamma $
generated by S. If
$\Gamma $
generated by S. If
![]() $\Gamma $
is a countable group, and
$\Gamma $
is a countable group, and
![]() $\Gamma \curvearrowright (X,\mu )$
is a measure-preserving action, then
$\Gamma \curvearrowright (X,\mu )$
is a measure-preserving action, then
![]() ${\mathcal R}_{\Gamma ,X}=\{(x,gx):g\in \Gamma \}$
is a discrete, measure-preserving equivalence relation. We use the notation
${\mathcal R}_{\Gamma ,X}=\{(x,gx):g\in \Gamma \}$
is a discrete, measure-preserving equivalence relation. We use the notation
![]() ${\mathcal S}\leq {\mathcal R}$
to mean that
${\mathcal S}\leq {\mathcal R}$
to mean that
![]() ${\mathcal S}$
is a subequivalence relation of
${\mathcal S}$
is a subequivalence relation of
![]() ${\mathcal R}$
, namely a subset of
${\mathcal R}$
, namely a subset of
![]() ${\mathcal R}$
which is also an equivalence relation over
${\mathcal R}$
which is also an equivalence relation over
![]() $(X,\mu )$
. We often abuse terminology and say that
$(X,\mu )$
. We often abuse terminology and say that
![]() ${\mathcal S}$
is a subrelation of
${\mathcal S}$
is a subrelation of
![]() ${\mathcal R}$
, and leave it as implicit that
${\mathcal R}$
, and leave it as implicit that
![]() ${\mathcal S}$
should also be an equivalence relation. If
${\mathcal S}$
should also be an equivalence relation. If
![]() $(X,\mu )$
and
$(X,\mu )$
and
![]() $E\subseteq X$
is measurable we let
$E\subseteq X$
is measurable we let
If E has positive measure, then
![]() ${\mathcal R}|_{E}$
is a measure-preserving relation over the probability space
${\mathcal R}|_{E}$
is a measure-preserving relation over the probability space
![]() $(E,{\mu (E\cap \cdot )}/{\mu (E)})$
. We let
$(E,{\mu (E\cap \cdot )}/{\mu (E)})$
. We let
![]() $[{\mathcal R}]$
be the group of all bimeasurable bijections
$[{\mathcal R}]$
be the group of all bimeasurable bijections
![]() $\phi \colon X\to ~X$
so that
$\phi \colon X\to ~X$
so that
![]() $\phi (x)\in [x]_{{\mathcal R}}$
for almost every
$\phi (x)\in [x]_{{\mathcal R}}$
for almost every
![]() $x\in X$
. We identify two elements of
$x\in X$
. We identify two elements of
![]() $[{\mathcal R}]$
if they agree almost everywhere. We have a natural metric d on
$[{\mathcal R}]$
if they agree almost everywhere. We have a natural metric d on
![]() $[{\mathcal R}]$
given by
$[{\mathcal R}]$
given by
This is a complete, separable, translation-invariant metric on
![]() $[{\mathcal R}]$
and this turns
$[{\mathcal R}]$
and this turns
![]() $[{\mathcal R}]$
into a Polish group. We use
$[{\mathcal R}]$
into a Polish group. We use
![]() $\operatorname {Prob}([{\mathcal R}])$
for the Borel probability measures on
$\operatorname {Prob}([{\mathcal R}])$
for the Borel probability measures on
![]() $[{\mathcal R}]$
. Since
$[{\mathcal R}]$
. Since
![]() $[{\mathcal R}]$
is a Polish group, the space
$[{\mathcal R}]$
is a Polish group, the space
![]() $\operatorname {Prob}([{\mathcal R}])$
can be made into a semigroup under convolution; so if
$\operatorname {Prob}([{\mathcal R}])$
can be made into a semigroup under convolution; so if
![]() $\nu _{1},\nu _{2}\in \operatorname {Prob}([{\mathcal R}])$
, then
$\nu _{1},\nu _{2}\in \operatorname {Prob}([{\mathcal R}])$
, then
![]() $\nu _{1}*\nu _{2}\in \operatorname {Prob}([{\mathcal R}])$
is defined by
$\nu _{1}*\nu _{2}\in \operatorname {Prob}([{\mathcal R}])$
is defined by
Given a countable
![]() $\Gamma \leq [{\mathcal R}]$
, we say that
$\Gamma \leq [{\mathcal R}]$
, we say that
![]() $\Gamma $
generates
$\Gamma $
generates
![]() ${\mathcal R}$
if
${\mathcal R}$
if
![]() $\Gamma x=[x]_{{\mathcal R}}$
for almost every
$\Gamma x=[x]_{{\mathcal R}}$
for almost every
![]() $x\in X$
. Given a countably supported
$x\in X$
. Given a countably supported
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
, we say that
$\nu \in \operatorname {Prob}([{\mathcal R}])$
, we say that
![]() $\nu $
generates
$\nu $
generates
![]() ${\mathcal R}$
if
${\mathcal R}$
if
![]() $\langle \operatorname {supp}(\nu ) \rangle $
generates
$\langle \operatorname {supp}(\nu ) \rangle $
generates
![]() ${\mathcal R}$
, where
${\mathcal R}$
, where
![]() $\operatorname {supp}(\nu )=\{\phi \in [{\mathcal R}]:\nu (\phi )\ne 0\}$
. We say that
$\operatorname {supp}(\nu )=\{\phi \in [{\mathcal R}]:\nu (\phi )\ne 0\}$
. We say that
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
is symmetric if the map
$\nu \in \operatorname {Prob}([{\mathcal R}])$
is symmetric if the map
![]() $\phi \mapsto \phi ^{-1}$
preserves
$\phi \mapsto \phi ^{-1}$
preserves
![]() $\nu $
.
$\nu $
.
Let G be a graph. We write
![]() $V(G)$
and
$V(G)$
and
![]() $E(G)$
respectively for the vertex and the edge set of G. Let
$E(G)$
respectively for the vertex and the edge set of G. Let
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $r\in \mathbb N$
. The r-ball around v is denoted by
$r\in \mathbb N$
. The r-ball around v is denoted by
![]() $B_G(v,r)$
and the r-sphere by
$B_G(v,r)$
and the r-sphere by
![]() $S_G(v,r)$
.
$S_G(v,r)$
.
We use Vinogradov’s notation and write
![]() $f\ll g$
if
$f\ll g$
if
![]() $|f|$
is bounded by a constant times
$|f|$
is bounded by a constant times
![]() $|g|$
.
$|g|$
.
For a Banach space V, we let
![]() $B(V)$
be the space of continuous, linear operators
$B(V)$
be the space of continuous, linear operators
![]() ${T\colon V\to V}$
. For
${T\colon V\to V}$
. For
![]() $T\in B(V)$
, we set
$T\in B(V)$
, we set
At various times we will have to appeal to spectral theory of bounded self-adjoint operators on a Hilbert space. Since most standard references on this theory assume Hilbert spaces are complex, in order to make these applications most transparent all Hilbert spaces will be assumed complex throughout this paper.
2.1. Translation between percolation and equivalence relations
Some of our results are stated in the language of percolation theory but all our proofs will be based on measured equivalence relations and graphings. An invariant (edge) percolation on a unimodular random graph
![]() $(\mathcal G,o)$
is a random triple
$(\mathcal G,o)$
is a random triple
![]() $(\mathcal G,o,P)$
where P is a subset of edges of G and the distribution of the triple is invariant under the rerooting equivalence relation. The following proposition associates a probability-measure-preserving measured equivalence relation to a percolation is such a way that Theorem 1.1 can deduced from Theorem 1.2.
$(\mathcal G,o,P)$
where P is a subset of edges of G and the distribution of the triple is invariant under the rerooting equivalence relation. The following proposition associates a probability-measure-preserving measured equivalence relation to a percolation is such a way that Theorem 1.1 can deduced from Theorem 1.2.
Proposition 2.1. Let
![]() $(\mathcal G,o)$
be a unimodular random graph with an invariant percolation P. There exists a probability-measure-preserving countable equivalence relation
$(\mathcal G,o)$
be a unimodular random graph with an invariant percolation P. There exists a probability-measure-preserving countable equivalence relation
![]() $(\Omega _\#,\nu _\#,{\mathcal R})$
with a generating graphing
$(\Omega _\#,\nu _\#,{\mathcal R})$
with a generating graphing
![]() $(\varphi _i)_{i\in I}$
and a subrelation
$(\varphi _i)_{i\in I}$
and a subrelation
![]() ${\mathcal S}\subset {\mathcal R}$
such that the following statements hold.
${\mathcal S}\subset {\mathcal R}$
such that the following statements hold.
-
(1) The rooted graph
 $({\mathcal G}_\omega ,\omega )$
with the vertex set
$({\mathcal G}_\omega ,\omega )$
with the vertex set
 $[\omega ]_{\mathcal R}$
and the edge set
$[\omega ]_{\mathcal R}$
and the edge set
 $\{(\omega ', \varphi _i(\omega ')): \omega '\in [\omega ]_{{\mathcal R}}, i\in I\}$
has the same law as
$\{(\omega ', \varphi _i(\omega ')): \omega '\in [\omega ]_{{\mathcal R}}, i\in I\}$
has the same law as
 $({\mathcal G},o)$
.
$({\mathcal G},o)$
. -
(2) The law of the pairs
 $(P^o,{\mathcal G})$
where
$(P^o,{\mathcal G})$
where
 $P^o$
is the connected component of the percolation
$P^o$
is the connected component of the percolation
 $P\subset \mathcal G$
is the same as the law of
$P\subset \mathcal G$
is the same as the law of
 $([\omega ]_{\mathcal S}, {\mathcal G}_\omega )$
where
$([\omega ]_{\mathcal S}, {\mathcal G}_\omega )$
where
 $[\omega ]_{{\mathcal S}}\subset {\mathcal G}_\omega $
is the
$[\omega ]_{{\mathcal S}}\subset {\mathcal G}_\omega $
is the
 ${\mathcal S}$
equivalence class of
${\mathcal S}$
equivalence class of
 $\omega $
.
$\omega $
.
Proof. We follow closely the construction in [Reference Aldous and Lyons6, Example 9.9]. Let
![]() $\Omega $
be the space of pairs
$\Omega $
be the space of pairs
![]() $((G,o),S)$
where
$((G,o),S)$
where
![]() $(G,o)$
is a rooted graph of degree at most d and S is a subset of edges. The distribution of the percolation P is naturally a probability measure on
$(G,o)$
is a rooted graph of degree at most d and S is a subset of edges. The distribution of the percolation P is naturally a probability measure on
![]() $\Omega $
; let us call it
$\Omega $
; let us call it
![]() $\mu $
. Let
$\mu $
. Let
![]() $\Omega _\#$
be a the set of triples
$\Omega _\#$
be a the set of triples
![]() $((G,o),S,\unicode{x3bb} )$
, where
$((G,o),S,\unicode{x3bb} )$
, where
![]() $(G,o),S$
are as before and
$(G,o),S$
are as before and
![]() $\unicode{x3bb} $
is a two-coloring of the vertices of
$\unicode{x3bb} $
is a two-coloring of the vertices of
![]() $(G,o)$
. Let
$(G,o)$
. Let
![]() $\mu _\#$
be the distribution of the random triple
$\mu _\#$
be the distribution of the random triple
![]() $(({\mathcal G},o),P,\Lambda )$
, where
$(({\mathcal G},o),P,\Lambda )$
, where
![]() $\Lambda $
is an i.i.d. coloring. The space
$\Lambda $
is an i.i.d. coloring. The space
![]() $(\Omega _\#,\mu _\#)$
is equipped with a natural finite graphing
$(\Omega _\#,\mu _\#)$
is equipped with a natural finite graphing
![]() $\Phi $
in which
$\Phi $
in which
![]() $((G,o),S,\unicode{x3bb} ),((G',o'),S',\unicode{x3bb} ')$
are connected if and only if
$((G,o),S,\unicode{x3bb} ),((G',o'),S',\unicode{x3bb} ')$
are connected if and only if
![]() $G=G', S=S', \unicode{x3bb} =\unicode{x3bb} '$
, and
$G=G', S=S', \unicode{x3bb} =\unicode{x3bb} '$
, and
![]() $o'$
is a neighbor of o. The graphing
$o'$
is a neighbor of o. The graphing
![]() $\Phi $
spans the rerooting measured equivalence relation
$\Phi $
spans the rerooting measured equivalence relation
![]() ${\mathcal R}$
, which preserves
${\mathcal R}$
, which preserves
![]() $\mu _\#$
. For each point
$\mu _\#$
. For each point
![]() $\omega \in \Omega _\#$
, the equivalence class
$\omega \in \Omega _\#$
, the equivalence class
![]() $[\omega ]_{\mathcal R}$
is equipped with a bounded-degree graph structure
$[\omega ]_{\mathcal R}$
is equipped with a bounded-degree graph structure
![]() ${\mathcal G}_\omega $
. The resulting random rooted graph
${\mathcal G}_\omega $
. The resulting random rooted graph
![]() $({\mathcal G}_\omega ,\omega )$
has the same law as
$({\mathcal G}_\omega ,\omega )$
has the same law as
![]() $(\mathcal G,o)$
and the second coordinate has the same law as the percolation P. To construct the subrelation
$(\mathcal G,o)$
and the second coordinate has the same law as the percolation P. To construct the subrelation
![]() ${\mathcal S}$
, we select a subgraphing
${\mathcal S}$
, we select a subgraphing
![]() $\Phi '\subset \Phi $
where
$\Phi '\subset \Phi $
where
![]() $((G,o),S,\unicode{x3bb} ),((G',o'),S',\unicode{x3bb} ')$
are connected if and only if
$((G,o),S,\unicode{x3bb} ),((G',o'),S',\unicode{x3bb} ')$
are connected if and only if
![]() $G=G', S=S', \unicode{x3bb} =\unicode{x3bb} '$
, and
$G=G', S=S', \unicode{x3bb} =\unicode{x3bb} '$
, and
![]() $o'$
is a neighbor of o connected by an edge in S. In this way the connected component of P containing the root is given by the
$o'$
is a neighbor of o connected by an edge in S. In this way the connected component of P containing the root is given by the
![]() ${\mathcal S}$
-equivalence class of w in
${\mathcal S}$
-equivalence class of w in
![]() ${\mathcal G}_w$
.
${\mathcal G}_w$
.
3. Existence of the co-spectral radius for subrelations
Let
![]() ${\mathcal R}$
be an ergodic probability-measure-preserving equivalence relation over a standard probability space
${\mathcal R}$
be an ergodic probability-measure-preserving equivalence relation over a standard probability space
![]() $(X,\mu )$
and let
$(X,\mu )$
and let
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
be countably supported and symmetric, that is,
$\nu \in \operatorname {Prob}([{\mathcal R}])$
be countably supported and symmetric, that is,
![]() $\nu (\{\phi \})=\nu (\{\phi ^{-1}\})$
for all
$\nu (\{\phi \})=\nu (\{\phi ^{-1}\})$
for all
![]() $\phi \in [{\mathcal R}]$
. Consider a measurable subequivalence relation
$\phi \in [{\mathcal R}]$
. Consider a measurable subequivalence relation
![]() ${\mathcal S}\leq {\mathcal R}$
. For
${\mathcal S}\leq {\mathcal R}$
. For
![]() $x\in X$
, the measure
$x\in X$
, the measure
![]() $\nu $
determines a random walk on
$\nu $
determines a random walk on
![]() $[x]_{{\mathcal R}}$
with transition probabilities
$[x]_{{\mathcal R}}$
with transition probabilities
![]() $p_{y,z}=\nu (\{\phi :\phi (y)=z\})$
. For
$p_{y,z}=\nu (\{\phi :\phi (y)=z\})$
. For
![]() $n\in {\mathbb N}$
,
$n\in {\mathbb N}$
,
![]() $(x,y)\in {\mathcal R}$
, we let
$(x,y)\in {\mathcal R}$
, we let
![]() $p_{n,x,y}^{\nu }$
(respectively,
$p_{n,x,y}^{\nu }$
(respectively,
![]() $p_{n,x,{\mathcal S}}^{\nu }$
) be the probability that the random walk corresponding to
$p_{n,x,{\mathcal S}}^{\nu }$
) be the probability that the random walk corresponding to
![]() $\nu $
starting at x is at y after n steps (respectively, in
$\nu $
starting at x is at y after n steps (respectively, in
![]() $[x]_{{\mathcal S}}$
after n steps). By direct calculation,
$[x]_{{\mathcal S}}$
after n steps). By direct calculation,
If
![]() $\nu $
is clear from the context (which is the usually the case), we will use
$\nu $
is clear from the context (which is the usually the case), we will use
![]() $p_{n,x,{\mathcal S}},p_{n,x,x}$
instead of
$p_{n,x,{\mathcal S}},p_{n,x,x}$
instead of
![]() $p_{n,x,{\mathcal S}}^{\nu },p_{n,x,x}^{\nu }.$
We are interested in the existence of the co-spectral radius of
$p_{n,x,{\mathcal S}}^{\nu },p_{n,x,x}^{\nu }.$
We are interested in the existence of the co-spectral radius of
![]() ${\mathcal S}$
inside
${\mathcal S}$
inside
![]() ${\mathcal R}$
which is, by definition, the limit
${\mathcal R}$
which is, by definition, the limit
In particular, we will show that this limit exists almost surely. While there are easy examples where this limit genuinely depends upon x (see Example 3.23) we will show that in many cases it is almost surely constant and is the norm of a self-adjoint operator on a Hilbert space naturally associated to
![]() ${\mathcal S}\leq {\mathcal R}$
.
${\mathcal S}\leq {\mathcal R}$
.
This is, of course, motivated by the case of an inclusion of groups
![]() $\Delta \leq \Gamma .$
Here the existence of the co-spectral radius, as well as the fact that it is the norm of the corresponding Markov operator on
$\Delta \leq \Gamma .$
Here the existence of the co-spectral radius, as well as the fact that it is the norm of the corresponding Markov operator on
![]() $\ell ^{2}(\Gamma /\Delta )$
, is a non-trivial, but well-known, fact. In the case when
$\ell ^{2}(\Gamma /\Delta )$
, is a non-trivial, but well-known, fact. In the case when
![]() $\Gamma $
is finitely generated and
$\Gamma $
is finitely generated and
![]() $\nu $
is the uniform measure on a finite generating set of
$\nu $
is the uniform measure on a finite generating set of
![]() $\Gamma $
we are looking at a random walk on a Schreier graph and it is easier to see the existence of this limit using the natural action of
$\Gamma $
we are looking at a random walk on a Schreier graph and it is easier to see the existence of this limit using the natural action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Gamma /\Delta $
. Even in the case when
$\Gamma /\Delta $
. Even in the case when
![]() $\nu $
is not the uniform measure on a finite subset of
$\nu $
is not the uniform measure on a finite subset of
![]() $\Gamma $
the action
$\Gamma $
the action
![]() $\Gamma \curvearrowright \Gamma /\Delta $
naturally enters into the very definition of the Markov operator. In the relation case this presents a problem a priori.
$\Gamma \curvearrowright \Gamma /\Delta $
naturally enters into the very definition of the Markov operator. In the relation case this presents a problem a priori.
Because
![]() ${\mathcal S}$
is a subrelation of
${\mathcal S}$
is a subrelation of
![]() ${\mathcal R}$
, for
${\mathcal R}$
, for
![]() $x\in X$
we can divide
$x\in X$
we can divide
![]() $[x]_{{\mathcal R}}$
into
$[x]_{{\mathcal R}}$
into
![]() ${\mathcal S}$
-equivalence classes. We let
${\mathcal S}$
-equivalence classes. We let
![]() $[x]_{{\mathcal R}}/{\mathcal S}$
be the space of
$[x]_{{\mathcal R}}/{\mathcal S}$
be the space of
![]() ${\mathcal S}$
-equivalence classes in
${\mathcal S}$
-equivalence classes in
![]() $[x]_{{\mathcal R}}$
. The field of spaces
$[x]_{{\mathcal R}}$
. The field of spaces
![]() $[x]_{{\mathcal R}}/{\mathcal S}$
is analogous to
$[x]_{{\mathcal R}}/{\mathcal S}$
is analogous to
![]() $\Gamma /\Delta $
, and so we may consider
$\Gamma /\Delta $
, and so we may consider
![]() $\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
as analogous to
$\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
as analogous to
![]() $\ell ^{2}(\Gamma /\Delta )$
. However, there is no obvious natural action of
$\ell ^{2}(\Gamma /\Delta )$
. However, there is no obvious natural action of
![]() $[{\mathcal R}]$
on
$[{\mathcal R}]$
on
![]() $[x]_{{\mathcal R}}/{\mathcal S}$
and this makes it difficult to see how one would define a Markov operator, and thus the co-spectral radius. We proceed to explain how to navigate this difficulty by collecting the field of Hilbert spaces
$[x]_{{\mathcal R}}/{\mathcal S}$
and this makes it difficult to see how one would define a Markov operator, and thus the co-spectral radius. We proceed to explain how to navigate this difficulty by collecting the field of Hilbert spaces
![]() $\ell ^{2}([x]_{{\mathcal R}}/S)$
together in a natural object.
$\ell ^{2}([x]_{{\mathcal R}}/S)$
together in a natural object.
Definition 3.1. Let
![]() $(X,\mu )$
be a standard probability space. Then a measurable field of Hilbert spaces over X is a family
$(X,\mu )$
be a standard probability space. Then a measurable field of Hilbert spaces over X is a family
![]() $(\mathcal {H}_{x})_{x\in X}$
of separable Hilbert spaces, together with a family
$(\mathcal {H}_{x})_{x\in X}$
of separable Hilbert spaces, together with a family
![]() ${\operatorname {Meas}}(\mathcal {H}_{x})\subseteq \prod _{x\in X}\mathcal {H}_{x}$
so that:
${\operatorname {Meas}}(\mathcal {H}_{x})\subseteq \prod _{x\in X}\mathcal {H}_{x}$
so that:
-
• for every
 $(\xi _{x})_{x},(\eta _{x})_{x}\in {\operatorname {Meas}}(\mathcal {H}_{x})$
we have that
$(\xi _{x})_{x},(\eta _{x})_{x}\in {\operatorname {Meas}}(\mathcal {H}_{x})$
we have that
 $x\mapsto \langle \xi _{x},\eta _{x} \rangle $
is measurable;
$x\mapsto \langle \xi _{x},\eta _{x} \rangle $
is measurable; -
• if
 $\eta =(\eta _{x})_{x\in X}\in \prod _{x\in X}\mathcal {H}_{x}$
and
$\eta =(\eta _{x})_{x\in X}\in \prod _{x\in X}\mathcal {H}_{x}$
and
 $x\mapsto \langle \xi _{x},\eta _{x} \rangle $
is measurable for all
$x\mapsto \langle \xi _{x},\eta _{x} \rangle $
is measurable for all
 $\xi =(\xi _{x})_{x}\in {\operatorname {Meas}}(\mathcal {H}_{x}),$
then
$\xi =(\xi _{x})_{x}\in {\operatorname {Meas}}(\mathcal {H}_{x}),$
then
 $\eta \in {\operatorname {Meas}}(\mathcal {H}_{x})$
;
$\eta \in {\operatorname {Meas}}(\mathcal {H}_{x})$
; -
• there is a sequence
 $(\xi ^{(n)})_{n=1}^{\infty }$
with
$(\xi ^{(n)})_{n=1}^{\infty }$
with
 $\xi ^{(n)}=(\xi ^{(n)})_{x\in X}$
in
$\xi ^{(n)}=(\xi ^{(n)})_{x\in X}$
in
 ${\operatorname {Meas}}(\mathcal {H}_{x})$
so that
${\operatorname {Meas}}(\mathcal {H}_{x})$
so that
 ${\mathcal {H}_{x}=\overline {\operatorname {span}\{\xi ^{(n)}_{x}:n\in {\mathbb N}\}}}$
for almost every
${\mathcal {H}_{x}=\overline {\operatorname {span}\{\xi ^{(n)}_{x}:n\in {\mathbb N}\}}}$
for almost every
 $x\in X.$
$x\in X.$
The direct integral, denoted by
![]() $\int _{X}^{\oplus } \mathcal {H}_{x}\,d\mu (x),$
is defined to be all
$\int _{X}^{\oplus } \mathcal {H}_{x}\,d\mu (x),$
is defined to be all
![]() $\xi \in {\operatorname {Meas}}(\mathcal {H}_{x})$
so that
$\xi \in {\operatorname {Meas}}(\mathcal {H}_{x})$
so that
![]() $\int _{X}\|\xi _{x}\|^{2}\,d\mu (x)<\infty ,$
where we identify two elements of
$\int _{X}\|\xi _{x}\|^{2}\,d\mu (x)<\infty ,$
where we identify two elements of
![]() ${\operatorname {Meas}}(\mathcal {H}_{x})$
if they agree outside a set of measure zero. We put an inner product on
${\operatorname {Meas}}(\mathcal {H}_{x})$
if they agree outside a set of measure zero. We put an inner product on
![]() $\int _{X}^{\oplus }\mathcal {H}_{x}$
,
$\int _{X}^{\oplus }\mathcal {H}_{x}$
,
and this gives
![]() $\int _{X}^{\oplus }\mathcal {H}_{x}$
the structure of a Hilbert space.
$\int _{X}^{\oplus }\mathcal {H}_{x}$
the structure of a Hilbert space.
We shall typically drop ‘over X’ in ‘a measurable field of Hilbert space over X’ if X is clear from the context. For later use, if
![]() $(\mathcal {H}_{x})_{x}$
is a measurable field of Hilbert spaces, then given
$(\mathcal {H}_{x})_{x}$
is a measurable field of Hilbert spaces, then given
![]() $A\subseteq X$
measurable and
$A\subseteq X$
measurable and
![]() $\xi \in {\operatorname {Meas}}(\mathcal {H}_{x}),$
we let
$\xi \in {\operatorname {Meas}}(\mathcal {H}_{x}),$
we let
![]() $1_{A}\xi \in {\operatorname {Meas}}(\mathcal {H}_{x})$
be defined by
$1_{A}\xi \in {\operatorname {Meas}}(\mathcal {H}_{x})$
be defined by
In our case, we can give the family
![]() $(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))_{x}$
a measurable structure by declaring that
$(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))_{x}$
a measurable structure by declaring that
![]() $\xi =(\xi _{x})_{x}\in \prod _{x\in X}\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
is measurable if
$\xi =(\xi _{x})_{x}\in \prod _{x\in X}\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
is measurable if
![]() $x \mapsto \xi _{x}([\phi (x)]_{{\mathcal S}})$
is measurable, for all
$x \mapsto \xi _{x}([\phi (x)]_{{\mathcal S}})$
is measurable, for all
![]() $\phi \in [{\mathcal R}]$
. General facts about direct integral imply that this collection of measurable vectors satisfy the above axioms (see Lemma 3.4). So we can define
$\phi \in [{\mathcal R}]$
. General facts about direct integral imply that this collection of measurable vectors satisfy the above axioms (see Lemma 3.4). So we can define
![]() $L^{2}({\mathcal R}/{\mathcal S})$
by
$L^{2}({\mathcal R}/{\mathcal S})$
by
 $$ \begin{align*}L^{2}({\mathcal R}/{\mathcal S})=\int_{X}^{\bigoplus}\ell^{2}([x]_{{\mathcal R}}/{\mathcal S})\,d\mu(x).\end{align*} $$
$$ \begin{align*}L^{2}({\mathcal R}/{\mathcal S})=\int_{X}^{\bigoplus}\ell^{2}([x]_{{\mathcal R}}/{\mathcal S})\,d\mu(x).\end{align*} $$
As mentioned above, there is no obvious natural action of
![]() $[{\mathcal R}]$
on
$[{\mathcal R}]$
on
![]() $[x]_{{\mathcal R}}/{\mathcal S}$
. However, we do have a natural unitary representation of
$[x]_{{\mathcal R}}/{\mathcal S}$
. However, we do have a natural unitary representation of
![]() $[{\mathcal R}]$
on
$[{\mathcal R}]$
on
![]() $L^{2}({\mathcal R}/{\mathcal S})$
. Define
$L^{2}({\mathcal R}/{\mathcal S})$
. Define
by
We will not need it for this paper, but this can be regarded as a representation of
![]() ${\mathcal R}$
itself (a precise definition will be given in [Reference Abert, Fraczyk and Hayes2]). For our purposes, we simply note that we have natural Markov operators defined on
${\mathcal R}$
itself (a precise definition will be given in [Reference Abert, Fraczyk and Hayes2]). For our purposes, we simply note that we have natural Markov operators defined on
![]() $L^{2}({\mathcal R}/{\mathcal S})$
. Namely, for a countably supported
$L^{2}({\mathcal R}/{\mathcal S})$
. Namely, for a countably supported
![]() ${\nu \in \operatorname {Prob}([{\mathcal R}])}$
, we define
${\nu \in \operatorname {Prob}([{\mathcal R}])}$
, we define

Here we are mildly abusing notation and using
![]() $\nu (\phi )$
for
$\nu (\phi )$
for
![]() $\nu (\{\phi \})$
; this will not present problems since
$\nu (\{\phi \})$
; this will not present problems since
![]() $\nu $
is atomic.
$\nu $
is atomic.
Theorem 3.2. Let
![]() ${\mathcal R}$
be a measure-preserving equivalence with countable orbits over a standard probability space
${\mathcal R}$
be a measure-preserving equivalence with countable orbits over a standard probability space
![]() $(X,\mu )$
, and let
$(X,\mu )$
, and let
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
be atomic. Suppose that the support of
$\nu \in \operatorname {Prob}([{\mathcal R}])$
be atomic. Suppose that the support of
![]() $\nu $
generates
$\nu $
generates
![]() ${\mathcal R}$
. Fix
${\mathcal R}$
. Fix
![]() ${\mathcal S}\leq {\mathcal R}$
.
${\mathcal S}\leq {\mathcal R}$
.
-
(i) The limit
exists. Moreover, $$ \begin{align*}\rho({\mathcal R}/{\mathcal S},\nu):=\lim_{n\to\infty}\bigg(\int p_{2n,x,\mathcal{S}}\,d\mu(x)\bigg)^{{1}/{2n}}\end{align*} $$
$$ \begin{align*}\rho({\mathcal R}/{\mathcal S},\nu):=\lim_{n\to\infty}\bigg(\int p_{2n,x,\mathcal{S}}\,d\mu(x)\bigg)^{{1}/{2n}}\end{align*} $$

-
(ii) The pointwise limit
exists almost surely, and $$ \begin{align*}\rho_{\nu}^{{\mathcal S}}(x)=\lim_{n\to\infty}p_{2n,x,{\mathcal S}}^{1/2n}\end{align*} $$
$$ \begin{align*}\rho_{\nu}^{{\mathcal S}}(x)=\lim_{n\to\infty}p_{2n,x,{\mathcal S}}^{1/2n}\end{align*} $$
 $$ \begin{align*}\rho({\mathcal R}/{\mathcal S},\nu)=\|\rho_{\nu}^{{\mathcal S}}\|_{\infty}.\end{align*} $$
$$ \begin{align*}\rho({\mathcal R}/{\mathcal S},\nu)=\|\rho_{\nu}^{{\mathcal S}}\|_{\infty}.\end{align*} $$
-
(iii) Suppose that the partial one-sided normalizer of
 ${\mathcal S}\leq {\mathcal R}$
acts ergodically (see Definition 3.14 for the definition). Then
${\mathcal S}\leq {\mathcal R}$
acts ergodically (see Definition 3.14 for the definition). Then
 $\rho _{\nu }^{{\mathcal S}}$
is almost surely constant, and by (ii) equals
$\rho _{\nu }^{{\mathcal S}}$
is almost surely constant, and by (ii) equals
 $\rho ({\mathcal R}/{\mathcal S},\nu )$
. In particular, this applies if
$\rho ({\mathcal R}/{\mathcal S},\nu )$
. In particular, this applies if
 ${\mathcal S}$
is normal or ergodic.
${\mathcal S}$
is normal or ergodic.
We will often drop the
![]() $\nu $
from
$\nu $
from
![]() $\rho ^{{\mathcal S}}_{\nu }$
if it is clear from context, and simply write
$\rho ^{{\mathcal S}}_{\nu }$
if it is clear from context, and simply write
![]() $\rho ^{{\mathcal S}}$
. Let
$\rho ^{{\mathcal S}}$
. Let
![]() $X,\mu ,{\mathcal R}$
be as in Theorem 3.2. Suppose that
$X,\mu ,{\mathcal R}$
be as in Theorem 3.2. Suppose that
![]() $y\in X$
and that the limit defining
$y\in X$
and that the limit defining
![]() $\rho ^{{\mathcal S}}(y)$
exists. Given
$\rho ^{{\mathcal S}}(y)$
exists. Given
![]() $x\in [y]_{{\mathcal R}}$
, choose a
$x\in [y]_{{\mathcal R}}$
, choose a
![]() $k\in {\mathbb N}$
with
$k\in {\mathbb N}$
with
![]() $p_{2k,x,y}>0$
. Then
$p_{2k,x,y}>0$
. Then
and so the limit
exists and equals
![]() $\rho ^{{\mathcal S}}(y)$
. If
$\rho ^{{\mathcal S}}(y)$
. If
![]() $\nu $
is assumed lazy, then
$\nu $
is assumed lazy, then
and so
exists and equals
![]() $\rho ^{{\mathcal S}}(x)$
. Thus, Theorem 3.2 recovers Theorem 1.2.
$\rho ^{{\mathcal S}}(x)$
. Thus, Theorem 3.2 recovers Theorem 1.2.
Remark 3.3. A co-spectral radius for normal subrelations also occurs in [Reference Bowen, Hoff and Ioana10, Lemma 6.7]; however, in that context the subrelation is both normal and ergodic, which gives a well-defined quotient group. If the subrelation is normal, there is a quotient groupoid [Reference Feldman, Sutherland and Zimmer15]; however, our situation is general enough (encompassing when the subrelation is ergodic or when it is normal) that we cannot appeal directly to the group case as in [Reference Bowen, Hoff and Ioana10]. We remark that the space
![]() $L^{2}({\mathcal R}/{\mathcal S})$
is closely related to the relation
$L^{2}({\mathcal R}/{\mathcal S})$
is closely related to the relation
![]() $\widehat {{\mathcal S}}$
that appears in [Reference Feldman, Sutherland and Zimmer15, Definition 1.4] (we caution the reader that the roles of
$\widehat {{\mathcal S}}$
that appears in [Reference Feldman, Sutherland and Zimmer15, Definition 1.4] (we caution the reader that the roles of
![]() ${\mathcal S},{\mathcal R}$
are reversed in [Reference Feldman, Sutherland and Zimmer15] relative to our work and so this relation is denoted
${\mathcal S},{\mathcal R}$
are reversed in [Reference Feldman, Sutherland and Zimmer15] relative to our work and so this relation is denoted
![]() $\widehat {{\mathcal R}}$
there), which is a measure-preserving relation on the space
$\widehat {{\mathcal R}}$
there), which is a measure-preserving relation on the space
![]() $Y=\{(x,c):x\in X,c\in [x]_{{\mathcal R}}/{\mathcal S}\}$
.
$Y=\{(x,c):x\in X,c\in [x]_{{\mathcal R}}/{\mathcal S}\}$
.
Explicitly,
We proceed to explain how they are related. Since we not explicitly use the connection between
![]() $L^{2}({\mathcal R}/{\mathcal S})$
and
$L^{2}({\mathcal R}/{\mathcal S})$
and
![]() $L^{2}(\widehat {{\mathcal S}})$
, we will only sketch the details.
$L^{2}(\widehat {{\mathcal S}})$
, we will only sketch the details.
In [Reference Abert, Fraczyk and Hayes2], we will explain how to give Y the structure of a standard Borel space and equip it with a natural
![]() $\sigma $
-finite measure. This measure will be defined in such a way as to make
$\sigma $
-finite measure. This measure will be defined in such a way as to make
![]() $L^{2}(Y)$
naturally unitarily isomorphic to
$L^{2}(Y)$
naturally unitarily isomorphic to
![]() $L^{2}({\mathcal R}/{\mathcal S})$
. We also have an isometric embedding V of
$L^{2}({\mathcal R}/{\mathcal S})$
. We also have an isometric embedding V of
![]() $L^{2}({\mathcal R}/{\mathcal S})$
into
$L^{2}({\mathcal R}/{\mathcal S})$
into
![]() $L^{2}(\widehat {{\mathcal S}})$
given by
$L^{2}(\widehat {{\mathcal S}})$
given by
Part of the significance of the relation
![]() $\widehat {{\mathcal S}}$
for the results in [Reference Feldman, Sutherland and Zimmer15] is that certain properties of the inclusion
$\widehat {{\mathcal S}}$
for the results in [Reference Feldman, Sutherland and Zimmer15] is that certain properties of the inclusion
![]() ${\mathcal S}\leq {\mathcal R}$
(e.g., the index, normality) are reflected in terms of properties of the inclusion
${\mathcal S}\leq {\mathcal R}$
(e.g., the index, normality) are reflected in terms of properties of the inclusion
![]() ${\mathcal R}\leq \widehat {{\mathcal S}}$
. An alternative explanation for this can be given by von Neumann algebras. Let
${\mathcal R}\leq \widehat {{\mathcal S}}$
. An alternative explanation for this can be given by von Neumann algebras. Let
![]() $L({\mathcal S}),L({\mathcal R})$
be the von Neumann algebras of the equivalence relations
$L({\mathcal S}),L({\mathcal R})$
be the von Neumann algebras of the equivalence relations
![]() ${\mathcal S},{\mathcal R}$
as defined in [Reference Feldman and Moore14] (the analogous notation there is
${\mathcal S},{\mathcal R}$
as defined in [Reference Feldman and Moore14] (the analogous notation there is
![]() $M({\mathcal S}),M({\mathcal R})$
). We then have a natural inclusion of von Neumann algebras
$M({\mathcal S}),M({\mathcal R})$
). We then have a natural inclusion of von Neumann algebras
![]() $L({\mathcal S})\leq L({\mathcal R})$
. The von Neumann algebra
$L({\mathcal S})\leq L({\mathcal R})$
. The von Neumann algebra
![]() $L(\widehat {{\mathcal S}})$
can be realized as the basic construction
$L(\widehat {{\mathcal S}})$
can be realized as the basic construction
![]() $\widehat {M}=\langle L(R),e_{L(S)} \rangle $
, in the sense of Jones [Reference Jones25, §3], of
$\widehat {M}=\langle L(R),e_{L(S)} \rangle $
, in the sense of Jones [Reference Jones25, §3], of
![]() $L({\mathcal S})\leq L({\mathcal R})$
. For the interested reader, we remark that under this correspondence, the space
$L({\mathcal S})\leq L({\mathcal R})$
. For the interested reader, we remark that under this correspondence, the space
![]() $L^{2}({\mathcal R}/{\mathcal S})$
corresponds to the following subspace of
$L^{2}({\mathcal R}/{\mathcal S})$
corresponds to the following subspace of
![]() $L^{2}(\widehat {M})$
:
$L^{2}(\widehat {M})$
:
where
![]() $u_{\phi }$
are the canonical unitaries in
$u_{\phi }$
are the canonical unitaries in
![]() $L({\mathcal R})$
corresponding to the elements of
$L({\mathcal R})$
corresponding to the elements of
![]() $[{\mathcal R}]$
and
$[{\mathcal R}]$
and
![]() $e_{L({\mathcal S})}$
is the Jones projection corresponding to the inclusion
$e_{L({\mathcal S})}$
is the Jones projection corresponding to the inclusion
![]() $L({\mathcal S})\leq L({\mathcal R})$
(see [Reference Feldman, Sutherland and Zimmer15]). Moreover, the action of
$L({\mathcal S})\leq L({\mathcal R})$
(see [Reference Feldman, Sutherland and Zimmer15]). Moreover, the action of
![]() $[{\mathcal R}]$
naturally acts on
$[{\mathcal R}]$
naturally acts on
![]() ${\mathcal H}$
by conjugating by
${\mathcal H}$
by conjugating by
![]() $u_{\phi }$
, and this action is isomorphic to the action of
$u_{\phi }$
, and this action is isomorphic to the action of
![]() $[{\mathcal R}]$
on
$[{\mathcal R}]$
on
![]() $L^{2}({\mathcal R}/{\mathcal S})$
we define above. We refer to [Reference Jones25] and [Reference Brown and Ozawa11, Appendix F], for the appropriate definitions, which we will not need in this work.
$L^{2}({\mathcal R}/{\mathcal S})$
we define above. We refer to [Reference Jones25] and [Reference Brown and Ozawa11, Appendix F], for the appropriate definitions, which we will not need in this work.
We now proceed to prove (i) of the above theorem, whose proof is almost entirely operator theory.
3.1. Proof of Theorem 3.2(i)
The essential idea behind Theorem 3.2(i) is that we have a natural vector in
![]() $L^{2}({\mathcal R}/{\mathcal S})$
which is given by the measurable field
$L^{2}({\mathcal R}/{\mathcal S})$
which is given by the measurable field
![]() $\xi _{x}=\delta _{[x]_{{\mathcal S}}}.$
By a direct calculation, we have that
$\xi _{x}=\delta _{[x]_{{\mathcal S}}}.$
By a direct calculation, we have that
We then have to show that
Because
![]() $\nu $
is symmetric, the operator
$\nu $
is symmetric, the operator
![]() $\unicode{x3bb} _{{\mathcal S}}(\nu )$
is self-adjoint and the existence of the limit on the right-hand side follows from the spectral theorem [Reference Conway12, Theorems IX.2.2 and IX.2.3]. The limit on the right-hand side is also dominated by
$\unicode{x3bb} _{{\mathcal S}}(\nu )$
is self-adjoint and the existence of the limit on the right-hand side follows from the spectral theorem [Reference Conway12, Theorems IX.2.2 and IX.2.3]. The limit on the right-hand side is also dominated by
![]() $\|\unicode{x3bb} _{{\mathcal S}}(\nu )\|$
. We prove a general Hilbert space theorem which, after a small amount of work, will prove the reverse inequality. First, let us alleviate any concerns about the measurable structure defined on
$\|\unicode{x3bb} _{{\mathcal S}}(\nu )\|$
. We prove a general Hilbert space theorem which, after a small amount of work, will prove the reverse inequality. First, let us alleviate any concerns about the measurable structure defined on
![]() $(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))_{x\in X}$
.
$(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))_{x\in X}$
.
Lemma 3.4. Let
![]() ${\mathcal S}\leq {\mathcal R}$
be discrete measure-preserving equivalence relations over a standard probability space
${\mathcal S}\leq {\mathcal R}$
be discrete measure-preserving equivalence relations over a standard probability space
![]() $(X,\mu )$
. Define a family
$(X,\mu )$
. Define a family
![]() ${\operatorname {Meas}}(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))\subseteq \prod _{x\in X}\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
by saying that
${\operatorname {Meas}}(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))\subseteq \prod _{x\in X}\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
by saying that
![]() $(\xi _{x})_{x\in X}\in {\operatorname {Meas}}(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))$
if and only if for every
$(\xi _{x})_{x\in X}\in {\operatorname {Meas}}(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))$
if and only if for every
![]() $\phi \in [{\mathcal R}]$
the function
$\phi \in [{\mathcal R}]$
the function
![]() $X\to {\mathbb C}$
given by
$X\to {\mathbb C}$
given by
![]() $x\mapsto \xi _{x}([\phi (x)]_{{\mathcal S}})$
is measurable. Then the family
$x\mapsto \xi _{x}([\phi (x)]_{{\mathcal S}})$
is measurable. Then the family
![]() ${\operatorname {Meas}}(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))$
turns
${\operatorname {Meas}}(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))$
turns
![]() $(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))_{x}$
into a measurable field of Hilbert spaces.
$(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))_{x}$
into a measurable field of Hilbert spaces.
Proof. Fix a countable subgroup
![]() $\Gamma \leq [{\mathcal R}]$
so that
$\Gamma \leq [{\mathcal R}]$
so that
![]() $\Gamma x=[x]_{{\mathcal R}}$
for almost every x. We start by proving the following claim.
$\Gamma x=[x]_{{\mathcal R}}$
for almost every x. We start by proving the following claim.
Claim. A vector
![]() $\xi =(\xi _{x})_{x}\in \prod _{x\in X}\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
is in
$\xi =(\xi _{x})_{x}\in \prod _{x\in X}\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
is in
![]() ${\operatorname {Meas}}(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))$
if and only if the map
${\operatorname {Meas}}(\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S}))$
if and only if the map
![]() $x\mapsto \xi _{x}([\phi (x)]_{{\mathcal S}})$
is measurable for every
$x\mapsto \xi _{x}([\phi (x)]_{{\mathcal S}})$
is measurable for every
![]() $\phi \in \Gamma $
. If
$\phi \in \Gamma $
. If
![]() $\xi $
is measurable then, by definition,
$\xi $
is measurable then, by definition,
![]() $x\mapsto \xi _{x}([\phi (x)]_{{\mathcal S}})$
is measurable for every
$x\mapsto \xi _{x}([\phi (x)]_{{\mathcal S}})$
is measurable for every
![]() $\phi \in [{\mathcal R}]$
. In particular, this is true for
$\phi \in [{\mathcal R}]$
. In particular, this is true for
![]() $\phi \in \Gamma $
. Conversely, suppose that
$\phi \in \Gamma $
. Conversely, suppose that
![]() $x\mapsto \xi _{x}([\phi (x)]_{{\mathcal S}})$
is measurable for all
$x\mapsto \xi _{x}([\phi (x)]_{{\mathcal S}})$
is measurable for all
![]() $\phi \in \Gamma .$
Fix a
$\phi \in \Gamma .$
Fix a
![]() $\psi \in [{\mathcal R}]$
. We then have to show that
$\psi \in [{\mathcal R}]$
. We then have to show that
![]() $x\mapsto \xi _{x}([\psi (x)]_{{\mathcal S}})$
is measurable. Since
$x\mapsto \xi _{x}([\psi (x)]_{{\mathcal S}})$
is measurable. Since
![]() $\Gamma x=[x]_{{\mathcal R}}$
for almost every
$\Gamma x=[x]_{{\mathcal R}}$
for almost every
![]() $x\in X$
, we may find a disjoint family of sets
$x\in X$
, we may find a disjoint family of sets
![]() $(E_{\phi })_{\phi \in \ \Gamma }$
with
$(E_{\phi })_{\phi \in \ \Gamma }$
with
![]() $E_{\phi }\subseteq \{x\in X:\psi (x)=\phi (x)\}$
and so that
$E_{\phi }\subseteq \{x\in X:\psi (x)=\phi (x)\}$
and so that
![]() $\bigsqcup E_{\phi }$
is a co-null subset of X. Then
$\bigsqcup E_{\phi }$
is a co-null subset of X. Then
for almost every x (the sum above converges since the
![]() $E_{\phi }$
are disjoint). Since
$E_{\phi }$
are disjoint). Since
![]() $\Gamma $
is countable, this proves that
$\Gamma $
is countable, this proves that
![]() $x\mapsto \xi _{x}([\psi (x)]_{{\mathcal S}})$
is measurable, and this proves the claim.
$x\mapsto \xi _{x}([\psi (x)]_{{\mathcal S}})$
is measurable, and this proves the claim.
Having shown the claim, for
![]() $\phi \in \Gamma $
define
$\phi \in \Gamma $
define
![]() $\zeta _{\phi }\in \prod _{x\in X}\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
by
$\zeta _{\phi }\in \prod _{x\in X}\ell ^{2}([x]_{{\mathcal R}}/{\mathcal S})$
by
![]() $\zeta _{\phi ,x}=\delta _{[\phi (x)]_{{\mathcal S}}}$
. Then
$\zeta _{\phi ,x}=\delta _{[\phi (x)]_{{\mathcal S}}}$
. Then
for almost every
![]() $x\in X$
, and also
$x\in X$
, and also
![]() $\xi _{x}([\phi (x)]_{{\mathcal S}})=\langle \xi _{x},\delta _{\phi (x)} \rangle $
for all
$\xi _{x}([\phi (x)]_{{\mathcal S}})=\langle \xi _{x},\delta _{\phi (x)} \rangle $
for all
![]() $\phi \in [{\mathcal R}]$
. Moreover, for
$\phi \in [{\mathcal R}]$
. Moreover, for
![]() $\phi ,\psi \in \Gamma $
we have that
$\phi ,\psi \in \Gamma $
we have that
which is a measurable function of x. The lemma now follows from countability of
![]() $\Gamma $
and [Reference Takesaki37, Lemma IV.8.10].
$\Gamma $
and [Reference Takesaki37, Lemma IV.8.10].
We use the following well-known lemma (see, for example, [Reference Hutchcroft24, Equation 2.8] for a proof), which is the main way we will relate the operator norm of the Markov operator
![]() $\unicode{x3bb} _{{\mathcal S}}(\nu )$
to the growth of the matrix coefficients
$\unicode{x3bb} _{{\mathcal S}}(\nu )$
to the growth of the matrix coefficients
![]() $\langle \unicode{x3bb} _{{\mathcal S}}(\nu )^{2n}\xi ,\xi \rangle $
.
$\langle \unicode{x3bb} _{{\mathcal S}}(\nu )^{2n}\xi ,\xi \rangle $
.
Lemma 3.5. Let
![]() $\mathcal {H}$
be a Hilbert space and
$\mathcal {H}$
be a Hilbert space and
![]() $T\in B(\mathcal {H})$
self-adjoint. Let K be an index set, and let
$T\in B(\mathcal {H})$
self-adjoint. Let K be an index set, and let
![]() $(\xi _{k})_{k\in K}$
be a K-tuple of vectors in
$(\xi _{k})_{k\in K}$
be a K-tuple of vectors in
![]() $\mathcal {H}$
so that
$\mathcal {H}$
so that
![]() $\mathcal {H}=\overline {\operatorname {span}\{\xi _{k}:k\in K\}}.$
Then
$\mathcal {H}=\overline {\operatorname {span}\{\xi _{k}:k\in K\}}.$
Then
In order to apply this in the context of a direct integral of Hilbert spaces, the following density criterion will be useful.
Lemma 3.6. Let
![]() $(X,\mu )$
be a standard probability space. Let
$(X,\mu )$
be a standard probability space. Let
![]() $(\mathcal {H}_{x})_{x\in X}$
be a measurable family of Hilbert spaces over X and set
$(\mathcal {H}_{x})_{x\in X}$
be a measurable family of Hilbert spaces over X and set
![]() $\mathcal {H}=\int _{X}^{\bigoplus }\mathcal {H}_{x}.$
Suppose we have a sequence
$\mathcal {H}=\int _{X}^{\bigoplus }\mathcal {H}_{x}.$
Suppose we have a sequence
![]() $\xi _{n}=(\xi _{n,x})_{x\in X}\in {\operatorname {Meas}}(\mathcal {H}_{x})$
such that
$\xi _{n}=(\xi _{n,x})_{x\in X}\in {\operatorname {Meas}}(\mathcal {H}_{x})$
such that
for almost every
![]() $x\in X$
. Then
$x\in X$
. Then
Proof. Suppose that
![]() $\eta \in {\mathcal H}$
and that
$\eta \in {\mathcal H}$
and that
![]() $\langle \eta ,1_{A}\xi _{n} \rangle =0$
for every
$\langle \eta ,1_{A}\xi _{n} \rangle =0$
for every
![]() $n\in {\mathbb N}$
and every measurable
$n\in {\mathbb N}$
and every measurable
![]() $A\subseteq X$
. Then for every measurable
$A\subseteq X$
. Then for every measurable
![]() $A\subseteq X$
and every
$A\subseteq X$
and every
![]() $n\in {\mathbb N}$
we have
$n\in {\mathbb N}$
we have
Since this holds for every A, applying this with A being
![]() $\{x\in X:\operatorname {Re}(i^{j}\langle \eta _{x},\xi _{n,x} \rangle )>0\}$
for
$\{x\in X:\operatorname {Re}(i^{j}\langle \eta _{x},\xi _{n,x} \rangle )>0\}$
for
![]() $j=0,1,2,3$
, and taking real and imaginary parts of the above integral shows that that for every
$j=0,1,2,3$
, and taking real and imaginary parts of the above integral shows that that for every
![]() $n\in {\mathbb N}$
we have that
$n\in {\mathbb N}$
we have that
![]() $\langle \eta _{x},\xi _{n,x} \rangle =0$
for almost every
$\langle \eta _{x},\xi _{n,x} \rangle =0$
for almost every
![]() $x\in X$
. By countability, for almost every
$x\in X$
. By countability, for almost every
![]() $x\in X$
we have
$x\in X$
we have
![]() $\langle \eta _{x},\xi _{n,x} \rangle =0$
for all
$\langle \eta _{x},\xi _{n,x} \rangle =0$
for all
![]() $n\in {\mathbb N}$
. Since
$n\in {\mathbb N}$
. Since
![]() $\mathcal {H}_{x}=\overline {\operatorname {span}\{\xi _{n,x}:n\in {\mathbb N}\}}$
for almost every
$\mathcal {H}_{x}=\overline {\operatorname {span}\{\xi _{n,x}:n\in {\mathbb N}\}}$
for almost every
![]() $x\in X$
, we deduce that
$x\in X$
, we deduce that
![]() $\eta _{x}=0$
for almost every
$\eta _{x}=0$
for almost every
![]() $x\in X$
, that is
$x\in X$
, that is
![]() $\eta =0$
as an element of
$\eta =0$
as an element of
![]() ${\mathcal H}$
. Thus, we have shown that the only vector in
${\mathcal H}$
. Thus, we have shown that the only vector in
![]() ${\mathcal H}$
orthogonal to
${\mathcal H}$
orthogonal to
![]() $\{1_{A}\xi _{n}: n\in {\mathbb N}, A\subseteq X\text { is measurable}\}$
is the zero vector, and this implies that
$\{1_{A}\xi _{n}: n\in {\mathbb N}, A\subseteq X\text { is measurable}\}$
is the zero vector, and this implies that
Proof of Theorem 3.2(i)
Let
![]() $\xi \in L^{2}({\mathcal R}/{\mathcal S})$
be the measurable vector field given by
$\xi \in L^{2}({\mathcal R}/{\mathcal S})$
be the measurable vector field given by
![]() ${\xi _{x}=\delta _{[x]_{{\mathcal S}}}.}$
By direct calculation,
${\xi _{x}=\delta _{[x]_{{\mathcal S}}}.}$
By direct calculation,
By the spectral theorem, there is a probability measure
![]() $\eta $
on
$\eta $
on
![]() $[-\|\unicode{x3bb} _{S}(\nu )\|,\|\unicode{x3bb} _{S}(\nu )\|]$
so that
$[-\|\unicode{x3bb} _{S}(\nu )\|,\|\unicode{x3bb} _{S}(\nu )\|]$
so that
From this, we see that
![]() $\lim _{n\to \infty }\langle \unicode{x3bb} _{S}(\nu )^{2n}\xi ,\xi \rangle ^{{1}/{2n}}$
exists and is the
$\lim _{n\to \infty }\langle \unicode{x3bb} _{S}(\nu )^{2n}\xi ,\xi \rangle ^{{1}/{2n}}$
exists and is the
![]() $L^{\infty }$
-norm of t with respect to
$L^{\infty }$
-norm of t with respect to
![]() $\eta $
. Combining these results, we see that
$\eta $
. Combining these results, we see that
 $$ \begin{align*}\lim_{n\to\infty}\bigg(\int p_{2n,x,{\mathcal S}}\,d\mu(x)\bigg)^{1/2n}\end{align*} $$
$$ \begin{align*}\lim_{n\to\infty}\bigg(\int p_{2n,x,{\mathcal S}}\,d\mu(x)\bigg)^{1/2n}\end{align*} $$
exists. Call this limit
![]() $\rho ({\mathcal R}/{\mathcal S},\nu )$
as in the statement of the theorem.
$\rho ({\mathcal R}/{\mathcal S},\nu )$
as in the statement of the theorem.
We now turn to the proof that
![]() $\rho ({\mathcal R}/{\mathcal S},\nu )=\|\unicode{x3bb} _{{\mathcal S}}(\nu )\|$
. It follows from the logic in the preceding paragraph that
$\rho ({\mathcal R}/{\mathcal S},\nu )=\|\unicode{x3bb} _{{\mathcal S}}(\nu )\|$
. It follows from the logic in the preceding paragraph that
![]() $\rho ({\mathcal R}/{\mathcal S},\nu )\leq \|\unicode{x3bb} _{{\mathcal S}}(\nu )\|$
. Let
$\rho ({\mathcal R}/{\mathcal S},\nu )\leq \|\unicode{x3bb} _{{\mathcal S}}(\nu )\|$
. Let
![]() $\Gamma $
be the subgroup of
$\Gamma $
be the subgroup of
![]() $[{\mathcal R}]$
generated by the support of
$[{\mathcal R}]$
generated by the support of
![]() $\nu $
. Since
$\nu $
. Since
![]() $\nu $
generates
$\nu $
generates
![]() ${\mathcal R}$
, we have
${\mathcal R}$
, we have
![]() $[x]_{{\mathcal R}}=\Gamma x$
for almost every
$[x]_{{\mathcal R}}=\Gamma x$
for almost every
![]() $x\in X$
. By Lemma 3.6,
$x\in X$
. By Lemma 3.6,
has dense linear span in
![]() ${\mathcal H}$
. It thus suffices, by Lemma 3.5, to prove that
${\mathcal H}$
. It thus suffices, by Lemma 3.5, to prove that
for every measurable
![]() $A\subseteq X$
and
$A\subseteq X$
and
![]() $\phi \in \Gamma $
. It is direct to see that
$\phi \in \Gamma $
. It is direct to see that
for every measurable
![]() $A\subseteq X$
. So it simply suffices to show that
$A\subseteq X$
. So it simply suffices to show that
To prove (3.1), fix
![]() $\phi \in \Gamma .$
Let
$\phi \in \Gamma .$
Let
![]() $\phi ^{*}({\mathcal S})$
be the subrelation
$\phi ^{*}({\mathcal S})$
be the subrelation
![]() $\phi ^{*}({\mathcal S})=\{(\phi (x),\phi (y)):(x,y)\in ~{\mathcal S}\}$
. By direct computation,
$\phi ^{*}({\mathcal S})=\{(\phi (x),\phi (y)):(x,y)\in ~{\mathcal S}\}$
. By direct computation,
Choose
![]() $k\in {\mathbb N}$
so that
$k\in {\mathbb N}$
so that
![]() $c=\nu ^{*k}(\{\phi \})>0$
. Then for every
$c=\nu ^{*k}(\{\phi \})>0$
. Then for every
![]() $n\in {\mathbb N}$
we have that
$n\in {\mathbb N}$
we have that
 $$ \begin{align*}p_{2(n+k),x,{\mathcal S}}&=\sum_{y\in [x]_{{\mathcal S}}}p_{2(n+k),x,y}\geq \sum_{y\in [x]_{{\mathcal S}}}p_{k,x,\phi(x)}p_{2n,\phi(x),\phi(y)}p_{k,\phi(y),y}\\ &\geq c^{2}\sum_{y\in [x]_{{\mathcal S}}}p_{2n,\phi(x),\phi(y)}=c^{2}p_{2n,\phi(x),\phi^{*}({\mathcal S})}. \end{align*} $$
$$ \begin{align*}p_{2(n+k),x,{\mathcal S}}&=\sum_{y\in [x]_{{\mathcal S}}}p_{2(n+k),x,y}\geq \sum_{y\in [x]_{{\mathcal S}}}p_{k,x,\phi(x)}p_{2n,\phi(x),\phi(y)}p_{k,\phi(y),y}\\ &\geq c^{2}\sum_{y\in [x]_{{\mathcal S}}}p_{2n,\phi(x),\phi(y)}=c^{2}p_{2n,\phi(x),\phi^{*}({\mathcal S})}. \end{align*} $$
Integrating both sides, we obtain
Thus,

This proves (3.1), and so completes the proof of Theorem 3.2(i).
As mentioned in the introduction, Theorem 3.2 and our later work in §4 can be used to recover a result due to Schramm used in [Reference Kozma31], [Reference Hutchcroft21, Lemma 6.4], and [Reference Hutchcroft22, §3]. Indeed, given a percolation of a connected, regular, transitive graph G by §2.1, one can build an inclusion
![]() ${\mathcal S}\leq {\mathcal R}$
of relations on a standard probability space as well as a symmetric probability measure
${\mathcal S}\leq {\mathcal R}$
of relations on a standard probability space as well as a symmetric probability measure
![]() $\nu $
on
$\nu $
on
![]() $[{\mathcal R}]$
so that, in the notation of [Reference Hutchcroft21, Lemma 6.4], we have
$[{\mathcal R}]$
so that, in the notation of [Reference Hutchcroft21, Lemma 6.4], we have
For
![]() $p\in (0,1)$
, consider Bernoulli(p) edge percolation, where each edge is kept with probability p; let
$p\in (0,1)$
, consider Bernoulli(p) edge percolation, where each edge is kept with probability p; let
![]() ${\mathcal S}_{p}\leq {\mathcal R}_{p}$
be the corresponding inclusion of equivalence relations. Set
${\mathcal S}_{p}\leq {\mathcal R}_{p}$
be the corresponding inclusion of equivalence relations. Set
In the setup of the proof of Theorem 3.2(i), we have that
Since
![]() $\unicode{x3bb} _{{\mathcal S}}(\nu )$
is self-adjoint, the spectral theorem tells us that
$\unicode{x3bb} _{{\mathcal S}}(\nu )$
is self-adjoint, the spectral theorem tells us that

is increasing in n and Theorem 3.2(i) characterizes its supremum as
![]() $\|\unicode{x3bb} _{{\mathcal S}}(\nu )\|$
. Additionally, for every
$\|\unicode{x3bb} _{{\mathcal S}}(\nu )\|$
. Additionally, for every
![]() $n\in {\mathbb N}$
we have by Cauchy–Schwarz that
$n\in {\mathbb N}$
we have by Cauchy–Schwarz that

where in the last step we use self-adjointness of
![]() $\unicode{x3bb} _{{\mathcal S}}(\nu )$
. The construction of the inclusion
$\unicode{x3bb} _{{\mathcal S}}(\nu )$
. The construction of the inclusion
![]() ${\mathcal S}\leq {\mathcal R}$
forces that the spectral radius of G is equal to the co-spectral radius of
${\mathcal S}\leq {\mathcal R}$
forces that the spectral radius of G is equal to the co-spectral radius of
![]() ${\mathcal T}\leq {\mathcal R}$
where
${\mathcal T}\leq {\mathcal R}$
where
![]() ${\mathcal T}=\{(x,x):x\in X\}$
is the trivial relation. For Bernoulli(p) percolation with
${\mathcal T}=\{(x,x):x\in X\}$
is the trivial relation. For Bernoulli(p) percolation with
![]() $p<p_{c}$
, finiteness of the clusters tells us that
$p<p_{c}$
, finiteness of the clusters tells us that
![]() $[x]_{{\mathcal S}_{p}}$
is finite for almost every
$[x]_{{\mathcal S}_{p}}$
is finite for almost every
![]() $x\in X$
. We will later show (see Proposition 4.1) that this implies that
$x\in X$
. We will later show (see Proposition 4.1) that this implies that
![]() $\rho ({\mathcal R}/{\mathcal S}_{p},\nu )=\|\unicode{x3bb} _{{\mathcal S}_{p}}(\nu )\|\leq \|\unicode{x3bb} _{{\mathcal T}}(\nu )\|=\rho ({\mathcal R},\nu )$
. Using the standard monotone coupling of Bernoulli percolation [Reference Lyons and Peres33, §5.2], it is direct to see that
$\rho ({\mathcal R}/{\mathcal S}_{p},\nu )=\|\unicode{x3bb} _{{\mathcal S}_{p}}(\nu )\|\leq \|\unicode{x3bb} _{{\mathcal T}}(\nu )\|=\rho ({\mathcal R},\nu )$
. Using the standard monotone coupling of Bernoulli percolation [Reference Lyons and Peres33, §5.2], it is direct to see that
![]() $\|\unicode{x3bb} _{{\mathcal S}_{p}}(\nu )\|$
is semicontinuous and that
$\|\unicode{x3bb} _{{\mathcal S}_{p}}(\nu )\|$
is semicontinuous and that
![]() $\|\unicode{x3bb} _{{\mathcal S}_{p_{c}}}(\nu )\|\leq \|\unicode{x3bb} _{{\mathcal T}}(\nu )\|$
. Thus, we obtain the estimate of Schramm for connected, transitive graphs. With minor modifications, our results work for random walks on finite cost graphings (see Example 3.9 of §3.2). In this manner, we can recover the same estimate of Schramm when G is a connected, locally finite, transitive graph. As mentioned in the introduction, in the context of percolation all our proofs can be rephrased without equivalence relations and can be written in the language of percolation theory.
$\|\unicode{x3bb} _{{\mathcal S}_{p_{c}}}(\nu )\|\leq \|\unicode{x3bb} _{{\mathcal T}}(\nu )\|$
. Thus, we obtain the estimate of Schramm for connected, transitive graphs. With minor modifications, our results work for random walks on finite cost graphings (see Example 3.9 of §3.2). In this manner, we can recover the same estimate of Schramm when G is a connected, locally finite, transitive graph. As mentioned in the introduction, in the context of percolation all our proofs can be rephrased without equivalence relations and can be written in the language of percolation theory.
3.2. The 2–3 method and proof of Theorem 3.2(ii)
We now explain how to deduce the existence of the pointwise limit defining the co-spectral radius. We first state the general Theorem behind this existence and then explain why it applies to our setting, as well as to more general situations. For notation, if
![]() $f,g\colon {\mathcal R}\to [0,\infty ]$
are measurable, then we define their convolution to be the function
$f,g\colon {\mathcal R}\to [0,\infty ]$
are measurable, then we define their convolution to be the function
![]() $f*g\colon {\mathcal R}\to [0,\infty ]$
given by
$f*g\colon {\mathcal R}\to [0,\infty ]$
given by
Given a measurable
![]() $\pi \colon X\to {\mathbb C}$
, we say that
$\pi \colon X\to {\mathbb C}$
, we say that
![]() $f\colon {\mathcal R}\to [0,\infty ]$
is
$f\colon {\mathcal R}\to [0,\infty ]$
is
![]() $\pi $
-symmetric if
$\pi $
-symmetric if
![]() $\pi (x)f(x,y)=\pi (y)f(y,x)$
for almost every
$\pi (x)f(x,y)=\pi (y)f(y,x)$
for almost every
![]() $(x,y)\in {\mathcal R}$
. If
$(x,y)\in {\mathcal R}$
. If
![]() $\pi =1$
, we just say that f is symmetric.
$\pi =1$
, we just say that f is symmetric.
Theorem 3.7. Let
![]() ${\mathcal R}$
be a discrete, measure-preserving equivalence relation over a standard probability space
${\mathcal R}$
be a discrete, measure-preserving equivalence relation over a standard probability space
![]() $(X,\mu )$
, and fix
$(X,\mu )$
, and fix
![]() $\pi \in L^{1}(X,\mu )$
with
$\pi \in L^{1}(X,\mu )$
with
![]() $\pi (x)\in (0,\infty )$
for almost every
$\pi (x)\in (0,\infty )$
for almost every
![]() $x\in X$
. Let
$x\in X$
. Let
![]() $f_{k}\colon {\mathcal R}\to [0,\infty ]$
for
$f_{k}\colon {\mathcal R}\to [0,\infty ]$
for
![]() $k\geq 1$
be a sequence of measurable functions such that:
$k\geq 1$
be a sequence of measurable functions such that:
-
(a)
 $f_{k}$
is
$f_{k}$
is
 $\pi $
-symmetric for all
$\pi $
-symmetric for all
 $k\in {\mathbb N}$
;
$k\in {\mathbb N}$
; -
(b) for all
 $l,k\in {\mathbb N}$
we have
$l,k\in {\mathbb N}$
we have
 $\sum _{y\in [x]_{{\mathcal R}}}(f_{l}*f_{k})(x,y)\leq \sum _{y\in [x]_{{\mathcal R}}}f_{l+k}(x,y)$
for almost every
$\sum _{y\in [x]_{{\mathcal R}}}(f_{l}*f_{k})(x,y)\leq \sum _{y\in [x]_{{\mathcal R}}}f_{l+k}(x,y)$
for almost every
 $x\in X$
;
$x\in X$
; -
(c) for almost every
 $x\in X$
and every
$x\in X$
and every
 $k\in {\mathbb N}$
we have
$k\in {\mathbb N}$
we have
 $0<\sum _{y\in [x]_{{\mathcal R}}}f_{k}(x,y)<\infty $
;
$0<\sum _{y\in [x]_{{\mathcal R}}}f_{k}(x,y)<\infty $
; -
(d) there is a measurable
 $D\colon X\to (0,\infty )$
so that for almost every
$D\colon X\to (0,\infty )$
so that for almost every $$ \begin{align*}\sum_{y\in [x]_{{\mathcal R}}}f_{l+k}(x,y)\geq D(x)^{l}\sum_{y\in [x]_{{\mathcal R}}} f_{k}(x,y)\end{align*} $$
$$ \begin{align*}\sum_{y\in [x]_{{\mathcal R}}}f_{l+k}(x,y)\geq D(x)^{l}\sum_{y\in [x]_{{\mathcal R}}} f_{k}(x,y)\end{align*} $$
 $x\in X$
and every
$x\in X$
and every
 $l,k\in {\mathbb N}$
.
$l,k\in {\mathbb N}$
.
Then
 $$ \begin{align*}\widetilde{f}(x)=\lim_{k\to\infty}\bigg(\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg)^{1/k}\end{align*} $$
$$ \begin{align*}\widetilde{f}(x)=\lim_{k\to\infty}\bigg(\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg)^{1/k}\end{align*} $$
exists and is positive almost surely. Further:
-
(i) for every
 $k\in {\mathbb N}$
$k\in {\mathbb N}$
 $$ \begin{align*}\int\pi(x)\frac{\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)}{\widetilde{f}(x)^{k}}\,d\mu(x)\leq \int \pi\,d\mu;\end{align*} $$
$$ \begin{align*}\int\pi(x)\frac{\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)}{\widetilde{f}(x)^{k}}\,d\mu(x)\leq \int \pi\,d\mu;\end{align*} $$
-
(ii)
 $\lim _{k\to \infty }(\int \pi (x)\sum _{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\,d\mu (x))^{1/k}=\|\widetilde {f}\|_{\infty }.$
$\lim _{k\to \infty }(\int \pi (x)\sum _{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\,d\mu (x))^{1/k}=\|\widetilde {f}\|_{\infty }.$
The name ‘2–3’ refers to the way we are proving Theorem 3.7. In the proof we have two separate steps where we show that ‘typically’
![]() $\sum _{y}f_{2k}(x,y)\sim (\sum _y f_k(x,y))^2$
and
$\sum _{y}f_{2k}(x,y)\sim (\sum _y f_k(x,y))^2$
and
![]() $(\sum _y f_{3k}(x,y))\sim (\sum _y f_k(x,y))^3$
. Since
$(\sum _y f_{3k}(x,y))\sim (\sum _y f_k(x,y))^3$
. Since
![]() $2,3$
generate a multiplicative semigroup which is asymptotically dense on the logarithmic scale, we are able to deduce that the exponential growth of
$2,3$
generate a multiplicative semigroup which is asymptotically dense on the logarithmic scale, we are able to deduce that the exponential growth of
![]() $(\sum _y f_k(x,y))$
has a definite rate.
$(\sum _y f_k(x,y))$
has a definite rate.
Before jumping into the proof of Theorem 3.7, let us list several examples where it applies. For all of these examples, fix a discrete, measure-preserving equivalence relation
![]() ${\mathcal R}$
over a standard probability space
${\mathcal R}$
over a standard probability space
![]() $(X,\mu )$
and fix a
$(X,\mu )$
and fix a
![]() ${\mathcal S}\leq {\mathcal R}$
.
${\mathcal S}\leq {\mathcal R}$
.
Example 3.8. Fix a symmetric
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
. Define
$\nu \in \operatorname {Prob}([{\mathcal R}])$
. Define
It is direct to check that our hypotheses apply in this case with
![]() $\pi =1$
,
$\pi =1$
,
![]() $D(x)=p_{2,x,x}$
. In this case
$D(x)=p_{2,x,x}$
. In this case
 $$ \begin{align*}\sum_{y\in [x]_{{\mathcal S}}}f_{k}(x,y)=p_{2k,x,{\mathcal S}},\end{align*} $$
$$ \begin{align*}\sum_{y\in [x]_{{\mathcal S}}}f_{k}(x,y)=p_{2k,x,{\mathcal S}},\end{align*} $$
and we recover the existence of the pointwise co-spectral radius
![]() $\rho ^{{\mathcal S}}_{\nu }$
. Moreover, item (ii) of Theorem 3.7 as well as Theorem 3.2(i) imply that
$\rho ^{{\mathcal S}}_{\nu }$
. Moreover, item (ii) of Theorem 3.7 as well as Theorem 3.2(i) imply that
So we recover the operator norm of the Markov operator
![]() $\unicode{x3bb} _{{\mathcal S}}(\nu )$
as the
$\unicode{x3bb} _{{\mathcal S}}(\nu )$
as the
![]() $L^{\infty }$
-norm of
$L^{\infty }$
-norm of
![]() $\rho ^{{\mathcal S}}_{\nu }$
.
$\rho ^{{\mathcal S}}_{\nu }$
.
Example 3.9. Suppose that
![]() $\nu \colon {\mathcal R}\to [0,1]$
is measurable and that
$\nu \colon {\mathcal R}\to [0,1]$
is measurable and that
![]() ${\sum _{y\in [x]_{{\mathcal R}}}\nu (x,y)=1}$
for almost every
${\sum _{y\in [x]_{{\mathcal R}}}\nu (x,y)=1}$
for almost every
![]() $x\in X$
. Moreover, assume that there is a
$x\in X$
. Moreover, assume that there is a
![]() $\pi \colon X\to (0,\infty )$
with
$\pi \colon X\to (0,\infty )$
with
![]() ${\pi \in L^{1}(X,\mu )}$
so that
${\pi \in L^{1}(X,\mu )}$
so that
![]() $\nu $
is
$\nu $
is
![]() $\pi $
-symmetric. Consider the Markov chain on
$\pi $
-symmetric. Consider the Markov chain on
![]() $[x]_{{\mathcal R}}$
with transition probabilities
$[x]_{{\mathcal R}}$
with transition probabilities
![]() $\nu (x,y)$
, and for
$\nu (x,y)$
, and for
![]() $k\in {\mathbb N}$
and
$k\in {\mathbb N}$
and
![]() $(x,y)\in {\mathcal R}$
let
$(x,y)\in {\mathcal R}$
let
![]() $p_{k,x,y}$
be the probability that the random walk corresponding to this Markov chain starting at x is at y after k steps. Set
$p_{k,x,y}$
be the probability that the random walk corresponding to this Markov chain starting at x is at y after k steps. Set
and
![]() $p_{2k,x,{\mathcal S}}=\sum _{y\in [x]_{{\mathcal S}}}p_{2k,x,y}$
. Note that if
$p_{2k,x,{\mathcal S}}=\sum _{y\in [x]_{{\mathcal S}}}p_{2k,x,y}$
. Note that if
![]() $f,g\colon {\mathcal R}\to [0,\infty ]$
are
$f,g\colon {\mathcal R}\to [0,\infty ]$
are
![]() $\pi $
-symmetric, then so is
$\pi $
-symmetric, then so is
![]() $f*g$
. Since
$f*g$
. Since
![]() $f_{k}=\nu ^{*2k}1_{S},$
we see that
$f_{k}=\nu ^{*2k}1_{S},$
we see that
![]() $f_{k}$
is
$f_{k}$
is
![]() $\pi $
-symmetric. Finally, observe that for every
$\pi $
-symmetric. Finally, observe that for every
![]() $x\in X,k\in {\mathbb N}$
,
$x\in X,k\in {\mathbb N}$
,
 $$ \begin{align*}0<p_{2,x,x}^{k}\leq p_{2k,x,x}\leq \sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\leq 1.\end{align*} $$
$$ \begin{align*}0<p_{2,x,x}^{k}\leq p_{2k,x,x}\leq \sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\leq 1.\end{align*} $$
So we deduce the existence of
A good example to keep in mind is the following. Recall that the full pseudogroup, denoted
![]() $[[{\mathcal R}]]$
, of
$[[{\mathcal R}]]$
, of
![]() ${\mathcal R}$
is by definition the set of bimeasurable bijections
${\mathcal R}$
is by definition the set of bimeasurable bijections
![]() $\phi \colon \operatorname {dom}(\phi )\to \operatorname {ran}(\phi )$
satisfying:
$\phi \colon \operatorname {dom}(\phi )\to \operatorname {ran}(\phi )$
satisfying:
-
•
 $\operatorname {dom}(\phi ),\operatorname {ran}(\phi )$
are measurable subsets of X;
$\operatorname {dom}(\phi ),\operatorname {ran}(\phi )$
are measurable subsets of X; -
•
 $\phi (x)\in [x]_{{\mathcal R}}$
for almost every
$\phi (x)\in [x]_{{\mathcal R}}$
for almost every
 $x\in X$
.
$x\in X$
.
We identify
![]() $\phi ,\psi \in [[{\mathcal R}]]$
if
$\phi ,\psi \in [[{\mathcal R}]]$
if
![]() $\mu (\operatorname {dom}(\phi )\Delta \operatorname {dom}(\psi ))=0$
and if
$\mu (\operatorname {dom}(\phi )\Delta \operatorname {dom}(\psi ))=0$
and if
![]() $\phi (x)=\psi (x)$
for almost every
$\phi (x)=\psi (x)$
for almost every
![]() $x\in \operatorname {dom}(\phi )\cap \operatorname {dom}(\psi )$
. For
$x\in \operatorname {dom}(\phi )\cap \operatorname {dom}(\psi )$
. For
![]() $\phi ,\psi \in [[{\mathcal R}]]$
we use
$\phi ,\psi \in [[{\mathcal R}]]$
we use
![]() $\phi \circ \psi $
for the element of
$\phi \circ \psi $
for the element of
![]() $[[{\mathcal R}]]$
whose domain is
$[[{\mathcal R}]]$
whose domain is
![]() $\operatorname {dom}(\psi )\cap \psi ^{-1}(\operatorname {dom}(\phi ))$
and which satisfies
$\operatorname {dom}(\psi )\cap \psi ^{-1}(\operatorname {dom}(\phi ))$
and which satisfies
![]() $\phi \circ \psi (x)=\phi (\psi (x))$
for
$\phi \circ \psi (x)=\phi (\psi (x))$
for
![]() $x\in \operatorname {dom}(\psi )\cap \psi ^{-1}(\operatorname {dom}(\phi ))$
. For
$x\in \operatorname {dom}(\psi )\cap \psi ^{-1}(\operatorname {dom}(\phi ))$
. For
![]() $\phi \in [[{\mathcal R}]]$
, we let
$\phi \in [[{\mathcal R}]]$
, we let
![]() $\phi ^{-1}$
be the element of
$\phi ^{-1}$
be the element of
![]() $[[{\mathcal R}]]$
with
$[[{\mathcal R}]]$
with
![]() $\operatorname {dom}(\phi ^{-1})=\operatorname {ran}(\phi )$
,
$\operatorname {dom}(\phi ^{-1})=\operatorname {ran}(\phi )$
,
![]() $\operatorname {ran}(\phi ^{-1})=\operatorname {dom}(\phi )$
, and so that
$\operatorname {ran}(\phi ^{-1})=\operatorname {dom}(\phi )$
, and so that
![]() $\phi ^{-1}(\phi (x))=x$
for all
$\phi ^{-1}(\phi (x))=x$
for all
![]() $x\in \operatorname {dom}(\phi )$
. Given a countable
$x\in \operatorname {dom}(\phi )$
. Given a countable
![]() $\Phi \subseteq [[{\mathcal R}]]$
and
$\Phi \subseteq [[{\mathcal R}]]$
and
![]() $x\in X$
we define a graph
$x\in X$
we define a graph
![]() $G_{\Phi ,x}$
whose vertex set is
$G_{\Phi ,x}$
whose vertex set is
![]() $[x]_{{\mathcal R}}$
and whose edge set is
$[x]_{{\mathcal R}}$
and whose edge set is
![]() $\bigcup _{\phi \in \Phi }\{\{y,\phi ^{\alpha }(y)\}:\alpha \in \{\pm 1\},y\in [x]_{{\mathcal R}}\cap \operatorname {dom}(\phi ^{\alpha })\}$
. We say that
$\bigcup _{\phi \in \Phi }\{\{y,\phi ^{\alpha }(y)\}:\alpha \in \{\pm 1\},y\in [x]_{{\mathcal R}}\cap \operatorname {dom}(\phi ^{\alpha })\}$
. We say that
![]() $\Phi $
is a graphing if
$\Phi $
is a graphing if
![]() $G_{\Phi ,x}$
is connected for almost every
$G_{\Phi ,x}$
is connected for almost every
![]() $x\in X$
. We define the cost of a graphing to be
$x\in X$
. We define the cost of a graphing to be
This definition is due to Levitt in [Reference Levitt32], and the cost of a relation (which is by definition the infimum of the cost of its graphings) was further systematically studied in [Reference Gaboriau18, Reference Gaboriau19]. If
![]() $\Phi $
is a finite cost graphing, then for almost every
$\Phi $
is a finite cost graphing, then for almost every
![]() $x\in X$
define
$x\in X$
define
![]() $\nu (x,y)={1}/{\deg _{G_{\Phi }}(x)}$
where
$\nu (x,y)={1}/{\deg _{G_{\Phi }}(x)}$
where
![]() $\deg _{G_{\Phi }}(x)$
is the degree of x in the graph
$\deg _{G_{\Phi }}(x)$
is the degree of x in the graph
![]() $G_{\Phi ,x}$
. Observe that
$G_{\Phi ,x}$
. Observe that
![]() $\nu $
is
$\nu $
is
![]() $\deg _{G,\Phi }$
-symmetric. Since
$\deg _{G,\Phi }$
-symmetric. Since
![]() $\int \deg _{G_{\Phi }}\,d\mu \leq 2c(\Phi )<\infty $
, we have a well-defined co-spectral radius for the simple random walk associated to finite cost graphings.
$\int \deg _{G_{\Phi }}\,d\mu \leq 2c(\Phi )<\infty $
, we have a well-defined co-spectral radius for the simple random walk associated to finite cost graphings.
Another good example is as follows. Consider a symmetric
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
, and
$\nu \in \operatorname {Prob}([{\mathcal R}])$
, and
![]() ${E\subseteq X}$
a measurable set with
${E\subseteq X}$
a measurable set with
![]() $\mu (E)>0$
. Assume that for almost every
$\mu (E)>0$
. Assume that for almost every
![]() $x\in E$
, we have that
$x\in E$
, we have that
![]() $\sum _{y\in [x]_{{\mathcal R}}\cap E}p_{x,y}>0$
(e.g., this holds if the random walk is lazy).
$\sum _{y\in [x]_{{\mathcal R}}\cap E}p_{x,y}>0$
(e.g., this holds if the random walk is lazy).
For
![]() $x\in X$
, define
$x\in X$
, define
![]() $\nu |_{E}\colon {\mathcal R}\cap (E\times E)\to [0,1]$
by
$\nu |_{E}\colon {\mathcal R}\cap (E\times E)\to [0,1]$
by
 $$ \begin{align*}\nu|_{E}(x,y)=\frac{p_{x,y}}{\sum_{y\in [x]_{{\mathcal R}}\cap E}p_{x,y}}.\end{align*} $$
$$ \begin{align*}\nu|_{E}(x,y)=\frac{p_{x,y}}{\sum_{y\in [x]_{{\mathcal R}}\cap E}p_{x,y}}.\end{align*} $$
As above this defines a Markov chain on
![]() $[x]_{{\mathcal R}}\cap E$
with transition probabilities given by
$[x]_{{\mathcal R}}\cap E$
with transition probabilities given by
![]() $\nu |_{E}$
. We have that
$\nu |_{E}$
. We have that
![]() $\nu |_{E}$
is
$\nu |_{E}$
is
![]() $\pi $
-symmetric, with
$\pi $
-symmetric, with
![]() $\pi (x,y)=\sum _{y\in [x]_{{\mathcal R}}\cap E}p_{x,y}$
. For
$\pi (x,y)=\sum _{y\in [x]_{{\mathcal R}}\cap E}p_{x,y}$
. For
![]() $k\in {\mathbb N}$
, we let
$k\in {\mathbb N}$
, we let
![]() $p^{\nu |_{E}}_{k,x,y}$
be the probability that the random walk starting at x with these transition probabilities is at y after k steps. Setting
$p^{\nu |_{E}}_{k,x,y}$
be the probability that the random walk starting at x with these transition probabilities is at y after k steps. Setting
![]() $p_{2k,x,{\mathcal S}|_{E}}^{\nu |_{E}}=\sum _{y\in [x]_{{\mathcal S}}\cap E}p^{\nu |_{E}}_{2k, x,y}$
, we deduce the almost sure existence of the ‘conditional’ co-spectral radius
$p_{2k,x,{\mathcal S}|_{E}}^{\nu |_{E}}=\sum _{y\in [x]_{{\mathcal S}}\cap E}p^{\nu |_{E}}_{2k, x,y}$
, we deduce the almost sure existence of the ‘conditional’ co-spectral radius
for
![]() $x\in E$
.
$x\in E$
.
Example 3.10. Fix a symmetric
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
and a measurable
$\nu \in \operatorname {Prob}([{\mathcal R}])$
and a measurable
![]() $E\subseteq X$
with
$E\subseteq X$
with
![]() $\mu (E)>0.$
Define
$\mu (E)>0.$
Define
In this case for
![]() $x\in E$
we have
$x\in E$
we have
 $$ \begin{align*}\sum_{y\in [x]_{{\mathcal S}}}f_{k}(x,y)=p_{2k,x,{\mathcal S},E}\end{align*} $$
$$ \begin{align*}\sum_{y\in [x]_{{\mathcal S}}}f_{k}(x,y)=p_{2k,x,{\mathcal S},E}\end{align*} $$
where
![]() $p_{2k,x,{\mathcal S},E}$
is the probability that the random walk corresponding to
$p_{2k,x,{\mathcal S},E}$
is the probability that the random walk corresponding to
![]() $\nu $
starting at x is in
$\nu $
starting at x is in
![]() $[x]_{{\mathcal S}}\cap E$
after
$[x]_{{\mathcal S}}\cap E$
after
![]() $2k$
steps. All of our hypotheses apply in this case with X replaced with E,
$2k$
steps. All of our hypotheses apply in this case with X replaced with E,
![]() ${\mathcal R}$
replaced with
${\mathcal R}$
replaced with
![]() ${\mathcal R}|_{E}$
, and
${\mathcal R}|_{E}$
, and
![]() $\pi =1$
. So we recover the existence of the pointwise local co-spectral radius
$\pi =1$
. So we recover the existence of the pointwise local co-spectral radius
at least for
![]() $x\in E$
. See §3.3 for more details. In that section we will show more generally that
$x\in E$
. See §3.3 for more details. In that section we will show more generally that
exists for almost every
![]() $x\in X$
; see Corollary 3.17. This specific example will be important for us when we show that the spectral radius is almost surely constant in the case that
$x\in X$
; see Corollary 3.17. This specific example will be important for us when we show that the spectral radius is almost surely constant in the case that
![]() ${\mathcal S}$
is either normal or ergodic.
${\mathcal S}$
is either normal or ergodic.
We say that a
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
is lazy if
$\nu \in \operatorname {Prob}([{\mathcal R}])$
is lazy if
![]() $\nu (\{\operatorname {id}\})>0$
.
$\nu (\{\operatorname {id}\})>0$
.
Example 3.11. Fix a lazy, symmetric
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
, and a measurable
$\nu \in \operatorname {Prob}([{\mathcal R}])$
, and a measurable
![]() $E\subseteq X$
with
$E\subseteq X$
with
![]() $\mu (E)>0.$
Define for
$\mu (E)>0.$
Define for
![]() $(x,y)\in {\mathcal R}$
:
$(x,y)\in {\mathcal R}$
:
 $$ \begin{align*}p_{2k,x,y,E}=\sum_{x_{1},\ldots,x_{2k-1}\in E}p_{x,x_{1}}p_{x_{1},x_{2}}\cdots p_{x_{2k-1},y},\end{align*} $$
$$ \begin{align*}p_{2k,x,y,E}=\sum_{x_{1},\ldots,x_{2k-1}\in E}p_{x,x_{1}}p_{x_{1},x_{2}}\cdots p_{x_{2k-1},y},\end{align*} $$
 $$ \begin{align*}p_{2k,x,{\mathcal S}|_{E}}=\sum_{\substack{x_{1},\ldots,x_{2k}\in E,\\ (x,x_{2k})\in {\mathcal S}}}p_{x,x_{1}}p_{x_{1},x_{2}}\cdots p_{x_{2k-1},x_{2k}}.\end{align*} $$
$$ \begin{align*}p_{2k,x,{\mathcal S}|_{E}}=\sum_{\substack{x_{1},\ldots,x_{2k}\in E,\\ (x,x_{2k})\in {\mathcal S}}}p_{x,x_{1}}p_{x_{1},x_{2}}\cdots p_{x_{2k-1},x_{2k}}.\end{align*} $$
Define
Then
 $$ \begin{align*}\sum_{y\in [x]_{{\mathcal S}}}f_{k}(x,y)=p_{2k,x,{\mathcal S}|_{E}}.\end{align*} $$
$$ \begin{align*}\sum_{y\in [x]_{{\mathcal S}}}f_{k}(x,y)=p_{2k,x,{\mathcal S}|_{E}}.\end{align*} $$
Again, it is direct to check that the hypotheses of Theorem 3.7 apply with
![]() $\pi =1$
. Note that laziness implies that
$\pi =1$
. Note that laziness implies that
for every
![]() $x\in E$
, and we always have
$x\in E$
, and we always have
Thus, (c) of Theorem 3.7 holds. So we deduce the existence of the ‘restricted’ co-spectral radius
for
![]() $x\in E$
. It can be shown by the same method of proof as in Theorem 3.2(i) that
$x\in E$
. It can be shown by the same method of proof as in Theorem 3.2(i) that

so
So we again recover the norm of a corner of the Markov operator as the essential supremum of the restricted co-spectral radius.
Example 3.12. Let
![]() $\varepsilon>0$
and let
$\varepsilon>0$
and let
![]() $\eta \colon {\mathcal R}\to [\varepsilon ,+\infty )$
be a measurable bounded symmetric function. Define for
$\eta \colon {\mathcal R}\to [\varepsilon ,+\infty )$
be a measurable bounded symmetric function. Define for
![]() $(x,y)\in {\mathcal R}$
:
$(x,y)\in {\mathcal R}$
:
Theorem 3.7 yields almost sure existence of the growth exponent
![]() $\rho _\eta :=\lim _{k\to \infty } (\sum _{y\in [x]_{\mathcal R}} f_k(x,y))^{1/k}.$
Let
$\rho _\eta :=\lim _{k\to \infty } (\sum _{y\in [x]_{\mathcal R}} f_k(x,y))^{1/k}.$
Let
![]() $\Phi \subset {\mathcal R}$
be a symmetric graphing generating
$\Phi \subset {\mathcal R}$
be a symmetric graphing generating
![]() ${\mathcal R}$
. If we put
${\mathcal R}$
. If we put
![]() $\eta =1_{\Phi }$
, we get the existence of the growth exponent for the number of trajectories of length
$\eta =1_{\Phi }$
, we get the existence of the growth exponent for the number of trajectories of length
![]() $2k$
starting at x in the graph induced by
$2k$
starting at x in the graph induced by
![]() $\Phi $
on the equivalence class of
$\Phi $
on the equivalence class of
![]() $[x]_{\mathcal R}$
. In particular, for every unimodular random graph
$[x]_{\mathcal R}$
. In particular, for every unimodular random graph
![]() $({\mathcal G},o)$
, the number of walks of length
$({\mathcal G},o)$
, the number of walks of length
![]() $2k$
starting from o has an exponential rate of growth almost surely. Note that such a result is definitely not true for any rooted bounded degree graph. This last example is discussed in more detail in §5.2.
$2k$
starting from o has an exponential rate of growth almost surely. Note that such a result is definitely not true for any rooted bounded degree graph. This last example is discussed in more detail in §5.2.
Having explained why Theorem 3.7 implies the existence of the pointwise co-spectral radius, we now turn to the proof of Theorem 3.7. The following is the main technical lemma behind the proof.
Lemma 3.13. Let
![]() $(f_{k})_{k},\pi $
be as in Theorem 3.7. For
$(f_{k})_{k},\pi $
be as in Theorem 3.7. For
![]() $k\in {\mathbb N}$
, define
$k\in {\mathbb N}$
, define
![]() $\widetilde {f}_{k}\colon X\to [0,\infty ]$
by
$\widetilde {f}_{k}\colon X\to [0,\infty ]$
by
 $$ \begin{align*}\widetilde{f}_{k}(x)=\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y),\end{align*} $$
$$ \begin{align*}\widetilde{f}_{k}(x)=\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y),\end{align*} $$
and define
 $$ \begin{align*}\phi_{k}(x)=\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\widetilde{f}_{k}(y)^{-1},\end{align*} $$
$$ \begin{align*}\phi_{k}(x)=\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\widetilde{f}_{k}(y)^{-1},\end{align*} $$
 $$ \begin{align*}\psi_{k}(x)=\widetilde{f}_{k}(x)\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg(\sum_{z\in [y]_{{\mathcal R}}}f_{k}(y,z)\widetilde{f}_{k}(z)\bigg)^{-1}\!.\end{align*} $$
$$ \begin{align*}\psi_{k}(x)=\widetilde{f}_{k}(x)\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg(\sum_{z\in [y]_{{\mathcal R}}}f_{k}(y,z)\widetilde{f}_{k}(z)\bigg)^{-1}\!.\end{align*} $$
Then:
-
(i) for every
 $k\in {\mathbb N}$
and almost every
$k\in {\mathbb N}$
and almost every
 $x\in X$
,
$x\in X$
,  $$ \begin{align*}\widetilde{f}_{k}(x)^{2}\leq \phi_{k}(x)\widetilde{f}_{2k}(x)\quad\text{and}\quad \widetilde{f}_{k}(x)^{3}\leq \psi_{k}(x)\widetilde{f}_{3k}(x);\end{align*} $$
$$ \begin{align*}\widetilde{f}_{k}(x)^{2}\leq \phi_{k}(x)\widetilde{f}_{2k}(x)\quad\text{and}\quad \widetilde{f}_{k}(x)^{3}\leq \psi_{k}(x)\widetilde{f}_{3k}(x);\end{align*} $$
-
(ii) for every
 $k\in {\mathbb N}$
,
$k\in {\mathbb N}$
,  $$ \begin{align*}\int \pi\phi_{k}\,d\mu=\int \pi\,d\mu=\int \pi\psi_{k}\,d\mu.\end{align*} $$
$$ \begin{align*}\int \pi\phi_{k}\,d\mu=\int \pi\,d\mu=\int \pi\psi_{k}\,d\mu.\end{align*} $$
Note that in order to make sense of
![]() $\phi _{k},\psi _{k}$
we are using hypothesis (c).
$\phi _{k},\psi _{k}$
we are using hypothesis (c).
Proof. (i) By Cauchy–Schwarz,
 $$ \begin{align*} \widetilde{f}_{k}(x)^{2}&=\bigg(\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)^{1/2}\widetilde{f}_{k}(y)^{-1/2}f_{k}(x,y)^{1/2}\widetilde{f}_{k}(y)^{1/2}\bigg)^{2}\\&\leq \phi_{k}(x)\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\widetilde{f}_{k}(y)\\ &\leq \phi_{k}(x)\widetilde{f}_{2k}(x) \end{align*} $$
$$ \begin{align*} \widetilde{f}_{k}(x)^{2}&=\bigg(\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)^{1/2}\widetilde{f}_{k}(y)^{-1/2}f_{k}(x,y)^{1/2}\widetilde{f}_{k}(y)^{1/2}\bigg)^{2}\\&\leq \phi_{k}(x)\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\widetilde{f}_{k}(y)\\ &\leq \phi_{k}(x)\widetilde{f}_{2k}(x) \end{align*} $$
for almost every
![]() $x\in X$
, where in the last step we use hypothesis (b). Using Cauchy–Schwarz again,
$x\in X$
, where in the last step we use hypothesis (b). Using Cauchy–Schwarz again,
 $$ \begin{align*}\widetilde{f}_{k}(x)^{2}\leq \widetilde{f}_{k}(x)^{-1}\psi_{k}(x)\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg(\sum_{z\in [y]_{{\mathcal R}}}f_{k}(y,z)\widetilde{f}_{k}(z)\bigg) \quad\text{for almost every } x\in X.\end{align*} $$
$$ \begin{align*}\widetilde{f}_{k}(x)^{2}\leq \widetilde{f}_{k}(x)^{-1}\psi_{k}(x)\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg(\sum_{z\in [y]_{{\mathcal R}}}f_{k}(y,z)\widetilde{f}_{k}(z)\bigg) \quad\text{for almost every } x\in X.\end{align*} $$
We can estimate the second sum using our hypothesis on
![]() $f_{k}$
:
$f_{k}$
:
 $$ \begin{align*} \sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg(\sum_{z\in [y]_{{\mathcal R}}}f_{k}(y,z)\widetilde{f}_{k}(z)\bigg)&=\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg(\sum_{w\in [y]_{{\mathcal R}}}(f_{k}*f_{k})(y,w)\bigg)\\ &\leq \sum_{w,y\in [x]_{{\mathcal R}}}f_{k}(x,y)f_{2k}(y,w)\\ &=\sum_{w\in [x]_{{\mathcal R}}}(f_{k}*f_{2k})(x,w)\\ &\leq \sum_{w\in [x]_{{\mathcal R}}}f_{3k}(x,w)\\ &=\widetilde{f}_{3k}(x), \end{align*} $$
$$ \begin{align*} \sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg(\sum_{z\in [y]_{{\mathcal R}}}f_{k}(y,z)\widetilde{f}_{k}(z)\bigg)&=\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg(\sum_{w\in [y]_{{\mathcal R}}}(f_{k}*f_{k})(y,w)\bigg)\\ &\leq \sum_{w,y\in [x]_{{\mathcal R}}}f_{k}(x,y)f_{2k}(y,w)\\ &=\sum_{w\in [x]_{{\mathcal R}}}(f_{k}*f_{2k})(x,w)\\ &\leq \sum_{w\in [x]_{{\mathcal R}}}f_{3k}(x,w)\\ &=\widetilde{f}_{3k}(x), \end{align*} $$
with all of the above inequalities and equalities holding for almost every
![]() $x\in X$
. So we have shown that
$x\in X$
. So we have shown that
and rearranging proves the desired inequality.
(ii) By the mass transport principle and
![]() $\pi $
-symmetry,
$\pi $
-symmetry,
 $$ \begin{align*}\int \pi(x)\phi_{k}(x)\,d\mu(x)=\int \sum_{y\in [x]_{{\mathcal R}}}\pi(x)f_{k}(x,y)\widetilde{f}_{k}(x)^{-1}\,d\mu(x)=\int \pi\,d\mu,\end{align*} $$
$$ \begin{align*}\int \pi(x)\phi_{k}(x)\,d\mu(x)=\int \sum_{y\in [x]_{{\mathcal R}}}\pi(x)f_{k}(x,y)\widetilde{f}_{k}(x)^{-1}\,d\mu(x)=\int \pi\,d\mu,\end{align*} $$
as
 $$ \begin{align*}\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\widetilde{f}_{k}(x)^{-1}=1.\end{align*} $$
$$ \begin{align*}\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\widetilde{f}_{k}(x)^{-1}=1.\end{align*} $$
Similarly,
 $$ \begin{align*}&\int \pi(x)\psi_{k}(x)\,d\mu(x)\\&\quad=\int \sum_{y\in [x]_{{\mathcal R}}}\pi(x)f_{k}(x,y)\widetilde{f}_{k}(y)\bigg(\sum_{z\in [x]_{{\mathcal R}}}f_{k}(x,z)\widetilde{f}_{k}(z)\bigg)^{-1}\,d\mu(x)=\int \pi\,d\mu,\end{align*} $$
$$ \begin{align*}&\int \pi(x)\psi_{k}(x)\,d\mu(x)\\&\quad=\int \sum_{y\in [x]_{{\mathcal R}}}\pi(x)f_{k}(x,y)\widetilde{f}_{k}(y)\bigg(\sum_{z\in [x]_{{\mathcal R}}}f_{k}(x,z)\widetilde{f}_{k}(z)\bigg)^{-1}\,d\mu(x)=\int \pi\,d\mu,\end{align*} $$
as
 $$ \begin{align*}\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\widetilde{f}_{k}(y)\bigg(\sum_{z\in [x]_{{\mathcal R}}}f_{k}(x,z)\widetilde{f}_{k}(z)\bigg)^{-1}=1.\\[-46pt]\end{align*} $$
$$ \begin{align*}\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\widetilde{f}_{k}(y)\bigg(\sum_{z\in [x]_{{\mathcal R}}}f_{k}(x,z)\widetilde{f}_{k}(z)\bigg)^{-1}=1.\\[-46pt]\end{align*} $$
We now prove Theorem 3.7. It will be helpful to pass to limits along subsets of
![]() ${\mathbb N}$
which are ‘not too sparse’ in a multiplicative sense. We say that
${\mathbb N}$
which are ‘not too sparse’ in a multiplicative sense. We say that
![]() $A\subseteq {\mathbb N}$
is asymptotically dense on the logarithmic scale if
$A\subseteq {\mathbb N}$
is asymptotically dense on the logarithmic scale if
We leave it as an exercise for the reader to show that if
![]() $A\subseteq {\mathbb N}$
is asymptotically dense on the logarithmic scale, and if
$A\subseteq {\mathbb N}$
is asymptotically dense on the logarithmic scale, and if
![]() $(a_{k})_{k=1}^{\infty }$
is a sequence of non-negative real numbers for which there is a uniform
$(a_{k})_{k=1}^{\infty }$
is a sequence of non-negative real numbers for which there is a uniform
![]() $C>0$
with
$C>0$
with
then
Proof of Theorem 3.7
Adopt notation as in Lemma 3.13. Set
For
![]() $p,q\in {\mathbb N}\cup \{0\},k\in {\mathbb N}$
we have, by Lemma 3.13 and induction, that
$p,q\in {\mathbb N}\cup \{0\},k\in {\mathbb N}$
we have, by Lemma 3.13 and induction, that
where
 $$ \begin{align*}C_{p,q,k}(x)=\prod_{i=0}^{p-1}\phi_{2^{i}k}(x)^{2^{p-1-i}3^{q}}\prod_{j=0}^{q-1}\psi_{2^{p}3^{j}k}(x)^{3^{q-1-j}}.\end{align*} $$
$$ \begin{align*}C_{p,q,k}(x)=\prod_{i=0}^{p-1}\phi_{2^{i}k}(x)^{2^{p-1-i}3^{q}}\prod_{j=0}^{q-1}\psi_{2^{p}3^{j}k}(x)^{3^{q-1-j}}.\end{align*} $$
By Lemma 3.13 and the fact that
![]() $\pi \in L^{1}(X,\mu )$
, both
$\pi \in L^{1}(X,\mu )$
, both
![]() $\sum _{k}k^{-2}\pi \phi _{k}$
and
$\sum _{k}k^{-2}\pi \phi _{k}$
and
![]() $\sum _{k}k^{-2}\pi \psi _{k}$
converge almost everywhere. Since
$\sum _{k}k^{-2}\pi \psi _{k}$
converge almost everywhere. Since
![]() $\pi (x)>0$
almost surely, we see that for almost every
$\pi (x)>0$
almost surely, we see that for almost every
![]() $x\in X$
, there is a
$x\in X$
, there is a
![]() $k_{0}$
(depending upon x) so that for
$k_{0}$
(depending upon x) so that for
![]() $k\geq k_{0}$
we have
$k\geq k_{0}$
we have
![]() $\phi _{k}(x)\leq k^{2}, \psi _{k}(x)\leq k^{2}$
. So for almost every
$\phi _{k}(x)\leq k^{2}, \psi _{k}(x)\leq k^{2}$
. So for almost every
![]() $x\in X$
, and for all
$x\in X$
, and for all
![]() $k\geq k_{0}$
, and all
$k\geq k_{0}$
, and all
![]() $p,q\in {\mathbb N}\cup \{0\}$
,
$p,q\in {\mathbb N}\cup \{0\}$
,
 $$ \begin{align*}C_{p,q,k}(x)\leq \prod_{i=0}^{p-1}(2^{i}k)^{2^{p-i}3^{q}}\prod_{j=0}^{q-1}(2^{p}3^{j}k)^{3^{q-1-j}2},\end{align*} $$
$$ \begin{align*}C_{p,q,k}(x)\leq \prod_{i=0}^{p-1}(2^{i}k)^{2^{p-i}3^{q}}\prod_{j=0}^{q-1}(2^{p}3^{j}k)^{3^{q-1-j}2},\end{align*} $$
which implies
 $$ \begin{align*}\frac{1}{2^{p}3^{q}}\log C_{p,q,k}(x)&\leq \sum_{i=0}^{p-1}2^{-i}\log(2^{i}k)+\sum_{j=0}^{q-1}2^{1-p}3^{-1-j}\log(2^{p}3^{j}k)\\ &\leq B+2\log(k), \end{align*} $$
$$ \begin{align*}\frac{1}{2^{p}3^{q}}\log C_{p,q,k}(x)&\leq \sum_{i=0}^{p-1}2^{-i}\log(2^{i}k)+\sum_{j=0}^{q-1}2^{1-p}3^{-1-j}\log(2^{p}3^{j}k)\\ &\leq B+2\log(k), \end{align*} $$
where
 $$ \begin{align*}B=\bigg(\max_{p\in {\mathbb N}\cup\{0\}}\frac{p}{2^{p}}\bigg)\log(2)+\log(2)\sum_{i=0}^{\infty}\frac{i}{2^{i}}+\frac{2\log(3)}{3}\sum_{j=0}^{\infty}\frac{j}{3^{j}}<\infty.\end{align*} $$
$$ \begin{align*}B=\bigg(\max_{p\in {\mathbb N}\cup\{0\}}\frac{p}{2^{p}}\bigg)\log(2)+\log(2)\sum_{i=0}^{\infty}\frac{i}{2^{i}}+\frac{2\log(3)}{3}\sum_{j=0}^{\infty}\frac{j}{3^{j}}<\infty.\end{align*} $$
Fix
![]() $k_{1}\geq k_{0}$
. Since
$k_{1}\geq k_{0}$
. Since
![]() $A=\{2^{p}3^{q}k_{1}:p,q\in {\mathbb N}\}$
is asymptotically dense on the logarithmic scale, we have by (3.2) and hypothesis (d) that
$A=\{2^{p}3^{q}k_{1}:p,q\in {\mathbb N}\}$
is asymptotically dense on the logarithmic scale, we have by (3.2) and hypothesis (d) that
 $$ \begin{align} \underline{f}(x)=\liminf_{p+q\to \infty}\widetilde{f}_{2^{p}3^{q}k_{1}}(x)^{{1}/{2^{p}3^{q}k_{1}}}&\geq \liminf_{p+q\to\infty}C_{p,q,k_{1}}(x)^{-{1}/{2^{p}3^{q}k_{1}}}\widetilde{f}_{k_{1}}(x)^{1/k_{1}}\nonumber\\ &\geq e^{-B/k_{1}}k_{1}^{-2/k_{1}}\widetilde{f}_{k_{1}}(x)^{1/k_{1}}. \end{align} $$
$$ \begin{align} \underline{f}(x)=\liminf_{p+q\to \infty}\widetilde{f}_{2^{p}3^{q}k_{1}}(x)^{{1}/{2^{p}3^{q}k_{1}}}&\geq \liminf_{p+q\to\infty}C_{p,q,k_{1}}(x)^{-{1}/{2^{p}3^{q}k_{1}}}\widetilde{f}_{k_{1}}(x)^{1/k_{1}}\nonumber\\ &\geq e^{-B/k_{1}}k_{1}^{-2/k_{1}}\widetilde{f}_{k_{1}}(x)^{1/k_{1}}. \end{align} $$
Letting
![]() $k_{1}\to \infty $
, we see that
$k_{1}\to \infty $
, we see that
![]() $\underline {f}\geq \overline {f}$
almost everywhere, and this proves that
$\underline {f}\geq \overline {f}$
almost everywhere, and this proves that
![]() $\widetilde {f}$
exists almost everywhere. Note that (3.3) applied with
$\widetilde {f}$
exists almost everywhere. Note that (3.3) applied with
![]() $k_{1}=k_{0}$
shows that
$k_{1}=k_{0}$
shows that
![]() ${\underline {f}(x)\geq e^{-B/k_{0}}k_{0}^{-2/k_{0}}\widetilde {f}_{k_{0}}(x)^{1/k_{0}}.}$
Thus,
${\underline {f}(x)\geq e^{-B/k_{0}}k_{0}^{-2/k_{0}}\widetilde {f}_{k_{0}}(x)^{1/k_{0}}.}$
Thus,
![]() $\widetilde {f}(x)>0$
for almost every x.
$\widetilde {f}(x)>0$
for almost every x.
(i) By (3.2), we have for
![]() $p,k\in {\mathbb N}$
and almost every
$p,k\in {\mathbb N}$
and almost every
![]() $x\in X$
that
$x\in X$
that
 $$ \begin{align*} \frac{\widetilde{f}_{k}(x)}{\widetilde{f}_{2^{p}k}(x)^{{1}/{2^{p}}}}\leq C_{p,0,k}(x)^{{1}/{2^{p}}}&=\bigg(\prod_{i=0}^{p-1}\phi_{2^{i+1}k}(x)^{2^{p-1-i}}\bigg)^{1/2^{p}}\\ &\leq \frac{1}{2^{p}}\bigg(1+\sum_{i=0}^{p-1}2^{p-1-i}\phi_{2^{i+1}k}(x)\bigg), \end{align*} $$
$$ \begin{align*} \frac{\widetilde{f}_{k}(x)}{\widetilde{f}_{2^{p}k}(x)^{{1}/{2^{p}}}}\leq C_{p,0,k}(x)^{{1}/{2^{p}}}&=\bigg(\prod_{i=0}^{p-1}\phi_{2^{i+1}k}(x)^{2^{p-1-i}}\bigg)^{1/2^{p}}\\ &\leq \frac{1}{2^{p}}\bigg(1+\sum_{i=0}^{p-1}2^{p-1-i}\phi_{2^{i+1}k}(x)\bigg), \end{align*} $$
where in the last step we use the arithmetic-geometric mean inequality. Lemma 3.13 implies that
 $$ \begin{align*}\int \pi(x)\frac{\widetilde{f}_{k}(x)}{\widetilde{f}_{2^{p}k}(x)^{{1}/{2^{p}}}}\,d\mu(x)\leq \int \pi\,d\mu.\end{align*} $$
$$ \begin{align*}\int \pi(x)\frac{\widetilde{f}_{k}(x)}{\widetilde{f}_{2^{p}k}(x)^{{1}/{2^{p}}}}\,d\mu(x)\leq \int \pi\,d\mu.\end{align*} $$
Letting
![]() $p\to \infty $
and applying Fatou’s lemma proves (i).
$p\to \infty $
and applying Fatou’s lemma proves (i).
(ii) Part (i) shows that
for every
![]() $k\in {\mathbb N}$
. Since
$k\in {\mathbb N}$
. Since
![]() $\pi \in L^{1}(X,\mu ),$
$\pi \in L^{1}(X,\mu ),$
 $$ \begin{align*}\limsup_{k\to\infty}\bigg(\int \pi(x)\widetilde{f}_{k}(x)\,d\mu(x)\bigg)^{{1}/{k}}\leq \|\widetilde{f}\|_{\infty}.\end{align*} $$
$$ \begin{align*}\limsup_{k\to\infty}\bigg(\int \pi(x)\widetilde{f}_{k}(x)\,d\mu(x)\bigg)^{{1}/{k}}\leq \|\widetilde{f}\|_{\infty}.\end{align*} $$
We now prove the reverse inequality. Fatou’s lemma implies that for all
![]() $r\in {\mathbb N}$
,
$r\in {\mathbb N}$
,
 $$ \begin{align*}\int \pi(x)\widetilde{f}(x)^{r}\,d\mu(x)&\leq \liminf_{k\to \infty}\int \pi(x)\widetilde{f}_{k}(x)^{{r}/{k}}\,d\mu(x)\\&\leq \liminf_{k\to\infty}\bigg(\int \pi(x)\widetilde{f}_{k}(x)\,d\mu(x)\bigg)^{{r}/{k}}\bigg(\int \pi(x)\,d\mu(x)\bigg)^{1-{r}/{k}}\!,\end{align*} $$
$$ \begin{align*}\int \pi(x)\widetilde{f}(x)^{r}\,d\mu(x)&\leq \liminf_{k\to \infty}\int \pi(x)\widetilde{f}_{k}(x)^{{r}/{k}}\,d\mu(x)\\&\leq \liminf_{k\to\infty}\bigg(\int \pi(x)\widetilde{f}_{k}(x)\,d\mu(x)\bigg)^{{r}/{k}}\bigg(\int \pi(x)\,d\mu(x)\bigg)^{1-{r}/{k}}\!,\end{align*} $$
where in the last step we use Holder’s inequality for
![]() $k>r$
. Since
$k>r$
. Since
![]() $\pi \in L^{1}(X,\mu )$
,
$\pi \in L^{1}(X,\mu )$
,
 $$ \begin{align*}\bigg(\int \pi(x)\widetilde{f}(x)^{r}\,d\mu(x)\bigg)^{{1}/{r}}\leq \liminf_{k\to\infty}\bigg(\int \pi(x) \widetilde{f}_{k}(x)\,d\mu(x)\bigg)^{{1}/{k}}.\end{align*} $$
$$ \begin{align*}\bigg(\int \pi(x)\widetilde{f}(x)^{r}\,d\mu(x)\bigg)^{{1}/{r}}\leq \liminf_{k\to\infty}\bigg(\int \pi(x) \widetilde{f}_{k}(x)\,d\mu(x)\bigg)^{{1}/{k}}.\end{align*} $$
Letting
![]() $r\to \infty $
and using that
$r\to \infty $
and using that
![]() $0<\pi (x)$
for almost every x and that
$0<\pi (x)$
for almost every x and that
![]() $\pi \in L^{1}(X,\mu )$
shows that
$\pi \in L^{1}(X,\mu )$
shows that
 $$ \begin{align*}\|\widetilde{f}\|_{\infty}\leq \liminf_{k\to\infty}\bigg(\int \pi(x)\widetilde{f}_{k}(x)\,d\mu(x)\bigg)^{{1}/{k}}\!.\\[-42pt]\end{align*} $$
$$ \begin{align*}\|\widetilde{f}\|_{\infty}\leq \liminf_{k\to\infty}\bigg(\int \pi(x)\widetilde{f}_{k}(x)\,d\mu(x)\bigg)^{{1}/{k}}\!.\\[-42pt]\end{align*} $$
3.3. Normal subrelations and the proof of Theorem 3.2(iii)
In this subsection we prove that the co-spectral radius
![]() $\rho ^{{\mathcal S}}(x)$
is almost surely constant when
$\rho ^{{\mathcal S}}(x)$
is almost surely constant when
![]() ${\mathcal S}$
is either ergodic normal (the case when
${\mathcal S}$
is either ergodic normal (the case when
![]() ${\mathcal S}$
is ergodic is fairly direct; see Corollary 3.17(a)). We prove a common generalization of the cases where
${\mathcal S}$
is ergodic is fairly direct; see Corollary 3.17(a)). We prove a common generalization of the cases where
![]() ${\mathcal S}$
is normal or ergodic, for which we need partial one-sided normalizers.
${\mathcal S}$
is normal or ergodic, for which we need partial one-sided normalizers.
Definition 3.14. Let
![]() $(X,\mu )$
be a standard probability space, and let
$(X,\mu )$
be a standard probability space, and let
![]() ${\mathcal S}\leq {\mathcal R}$
be discrete, measure-preserving equivalence relations on
${\mathcal S}\leq {\mathcal R}$
be discrete, measure-preserving equivalence relations on
![]() $(X,\mu )$
. We define the partial one-sided normalizers to be the set of
$(X,\mu )$
. We define the partial one-sided normalizers to be the set of
![]() $\phi \in [[{\mathcal R}]]$
such that for almost every
$\phi \in [[{\mathcal R}]]$
such that for almost every
![]() $x\in \operatorname {dom}(\phi )$
we have
$x\in \operatorname {dom}(\phi )$
we have
![]() $\phi ([x]_{{\mathcal S}}\cap \operatorname {dom}(\phi ))\subseteq [\phi (x)]_{{\mathcal S}}$
. We use
$\phi ([x]_{{\mathcal S}}\cap \operatorname {dom}(\phi ))\subseteq [\phi (x)]_{{\mathcal S}}$
. We use
![]() $PN_{{\mathcal R}}^{(1)}({\mathcal S})$
for the set of partial one-sided normalizers of
$PN_{{\mathcal R}}^{(1)}({\mathcal S})$
for the set of partial one-sided normalizers of
![]() ${\mathcal S}$
inside
${\mathcal S}$
inside
![]() ${\mathcal R}$
.
${\mathcal R}$
.
One example to keep in mind for intuition is as follows. Suppose that
![]() ${\mathcal R}$
is the orbit equivalence relation of a measure-preserving action of G on
${\mathcal R}$
is the orbit equivalence relation of a measure-preserving action of G on
![]() $(X,\mu )$
. Suppose that
$(X,\mu )$
. Suppose that
![]() $H\leq G$
, and let
$H\leq G$
, and let
![]() ${\mathcal S}=\{(x,ax):a\in N,x\in X\}$
. For
${\mathcal S}=\{(x,ax):a\in N,x\in X\}$
. For
![]() $g\in G$
, we let
$g\in G$
, we let
![]() $\phi _{g}\in [{\mathcal R}]$
be given by
$\phi _{g}\in [{\mathcal R}]$
be given by
![]() ${\phi _{g}(x)=gx}$
. If g is in the normalizer of H inside G, then by direct calculation
${\phi _{g}(x)=gx}$
. If g is in the normalizer of H inside G, then by direct calculation
![]() ${\phi _{g}([x]_{{\mathcal S}})=[x]_{{\mathcal S}}}$
for almost every
${\phi _{g}([x]_{{\mathcal S}})=[x]_{{\mathcal S}}}$
for almost every
![]() $x\in X$
. So
$x\in X$
. So
![]() $\phi _{g}\in PN_{{\mathcal R}}^{(1)}({\mathcal S})$
. More generally,
$\phi _{g}\in PN_{{\mathcal R}}^{(1)}({\mathcal S})$
. More generally,
![]() ${\phi _{g}|_{E}\in PN_{{\mathcal R}}^{(1)}({\mathcal S})}$
for every
${\phi _{g}|_{E}\in PN_{{\mathcal R}}^{(1)}({\mathcal S})}$
for every
![]() $g\in G$
in the normalizer of H. We can thus think of the partial one-sided normalizers as a generalization of normalizers to the setting of the full pseudogroup.
$g\in G$
in the normalizer of H. We can thus think of the partial one-sided normalizers as a generalization of normalizers to the setting of the full pseudogroup.
Another source of elements in the partial normalizer is as follows. Recall that the set of endomorphisms of
![]() ${\mathcal R}$
over
${\mathcal R}$
over
![]() ${\mathcal S}$
, denoted by
${\mathcal S}$
, denoted by
![]() $\operatorname {End}_{{\mathcal R}}({\mathcal S})$
, is constituted by the measurable functions
$\operatorname {End}_{{\mathcal R}}({\mathcal S})$
, is constituted by the measurable functions
![]() $\phi \colon X\to X$
such that for almost every
$\phi \colon X\to X$
such that for almost every
![]() $x\in X$
the following two conditions hold:
$x\in X$
the following two conditions hold:
-
•
 $\phi (x)\in [x]_{{\mathcal R}}$
;
$\phi (x)\in [x]_{{\mathcal R}}$
; -
•
 $\phi ([x]_{{\mathcal S}})\subseteq [\phi (x)]_{{\mathcal S}}$
.
$\phi ([x]_{{\mathcal S}})\subseteq [\phi (x)]_{{\mathcal S}}$
.
Such functions need not be injective modulo null sets, and when they fail to be injective modulo null sets are not measure-preserving. Indeed, one can use the mass-transport principle to show that for
![]() $\phi \in \operatorname {End}_{{\mathcal R}}({\mathcal S})$
we have that
$\phi \in \operatorname {End}_{{\mathcal R}}({\mathcal S})$
we have that
(we will not use this fact so will not give a full proof of it). However, as we will see shortly (see Lemma 3.16), for each
![]() $\phi \in \operatorname {End}_{{\mathcal R}}({\mathcal S})$
we may find a partition modulo null sets
$\phi \in \operatorname {End}_{{\mathcal R}}({\mathcal S})$
we may find a partition modulo null sets
![]() $(E_{i})_{i\in I}$
of X into countably many sets so that
$(E_{i})_{i\in I}$
of X into countably many sets so that
![]() $\phi |_{E_{i}}$
is injective for each
$\phi |_{E_{i}}$
is injective for each
![]() $i\in I$
.
$i\in I$
.
This last example in fact provides the motivation for our consideration of the one-sided partial normalizers, as this is one way to define normal subrelations.
Definition 3.15. (See Theorem 2.2 of [Reference Feldman and Moore14])
Let
![]() ${\mathcal R}$
be a discrete, measure-preserving equivalence relation on a standard probability space
${\mathcal R}$
be a discrete, measure-preserving equivalence relation on a standard probability space
![]() $(X,\mu )$
. A subrelation
$(X,\mu )$
. A subrelation
![]() ${\mathcal S}\leq {\mathcal R}$
is normal if there is a countable set
${\mathcal S}\leq {\mathcal R}$
is normal if there is a countable set
![]() $D\subseteq \operatorname {End}_{{\mathcal R}}({\mathcal S})$
so that
$D\subseteq \operatorname {End}_{{\mathcal R}}({\mathcal S})$
so that
![]() $[x]_{{\mathcal R}}=\bigcup _{\phi \in D}\phi ([x]_{{\mathcal S}})$
for almost every
$[x]_{{\mathcal R}}=\bigcup _{\phi \in D}\phi ([x]_{{\mathcal S}})$
for almost every
![]() $x\in X$
.
$x\in X$
.
From the above definition, one can imagine attempting to prove that the co-spectral radius is almost surely constant for a normal subrelation by trying to understand how it varies after applying endomorphisms of
![]() ${\mathcal S}\leq {\mathcal R}$
. However, as alluded to above, endomorphisms can have undesirable properties (namely, lack of injectivity and failure to be measure-preserving) and the possibility of these undesirability properties makes them ill-suited for our proofs. A good tradeoff for our purposes is to drop being everywhere defined and gain being measure-preserving and injective. This is precisely the purpose of the one-sided partial normalizers.
${\mathcal S}\leq {\mathcal R}$
. However, as alluded to above, endomorphisms can have undesirable properties (namely, lack of injectivity and failure to be measure-preserving) and the possibility of these undesirability properties makes them ill-suited for our proofs. A good tradeoff for our purposes is to drop being everywhere defined and gain being measure-preserving and injective. This is precisely the purpose of the one-sided partial normalizers.
We have a natural way for elements of
![]() $PN^{(1)}_{{\mathcal R}}({\mathcal S})$
to act on
$PN^{(1)}_{{\mathcal R}}({\mathcal S})$
to act on
![]() $L^{p}(X,\mu )$
for
$L^{p}(X,\mu )$
for
![]() $1\leq p\leq \infty $
. Namely, if
$1\leq p\leq \infty $
. Namely, if
![]() $\phi \in PN^{(1)}_{{\mathcal R}}({\mathcal S})$
we define
$\phi \in PN^{(1)}_{{\mathcal R}}({\mathcal S})$
we define
![]() $\alpha _{\phi }\in B(L^{p}(X,\mu ))$
via
$\alpha _{\phi }\in B(L^{p}(X,\mu ))$
via
This allows us to say what it means for
![]() $PN^{(1)}_{{\mathcal R}}({\mathcal S})$
to act ergodically. It simply means that if
$PN^{(1)}_{{\mathcal R}}({\mathcal S})$
to act ergodically. It simply means that if
![]() $f\in L^{p}(X,\mu )$
and
$f\in L^{p}(X,\mu )$
and
![]() $\alpha _{\phi }(f)=1_{\operatorname {ran}(\phi )}f$
for every
$\alpha _{\phi }(f)=1_{\operatorname {ran}(\phi )}f$
for every
![]() $\phi \in PN^{(1)}_{{\mathcal R}}({\mathcal S})$
, then f is essentially constant. We leave it as an exercise for the reader to follow the usual arguments to verify that this is equivalent to saying that there exists a countable
$\phi \in PN^{(1)}_{{\mathcal R}}({\mathcal S})$
, then f is essentially constant. We leave it as an exercise for the reader to follow the usual arguments to verify that this is equivalent to saying that there exists a countable
![]() $C\subseteq PN^{(1)}_{{\mathcal R}}({\mathcal S})$
so that if a measurable subset of X is invariant under C, then its measure is either
$C\subseteq PN^{(1)}_{{\mathcal R}}({\mathcal S})$
so that if a measurable subset of X is invariant under C, then its measure is either
![]() $0$
or
$0$
or
![]() $1$
. Note that
$1$
. Note that
![]() $PN^{(1)}_{{\mathcal R}}({\mathcal S})$
automatically acts ergodically if
$PN^{(1)}_{{\mathcal R}}({\mathcal S})$
automatically acts ergodically if
![]() ${\mathcal S}$
is ergodic, because
${\mathcal S}$
is ergodic, because
![]() $[{\mathcal S}]\subseteq PN^{(1)}_{{\mathcal R}}({\mathcal S})$
. The following lemma shows that
$[{\mathcal S}]\subseteq PN^{(1)}_{{\mathcal R}}({\mathcal S})$
. The following lemma shows that
![]() $PN^{(1)}_{{\mathcal R}}({\mathcal S})$
also acts ergodically if
$PN^{(1)}_{{\mathcal R}}({\mathcal S})$
also acts ergodically if
![]() ${\mathcal S}$
is normal and
${\mathcal S}$
is normal and
![]() ${\mathcal R}$
is ergodic.
${\mathcal R}$
is ergodic.
Lemma 3.16. Suppose that
![]() ${\mathcal S}$
is normal in
${\mathcal S}$
is normal in
![]() ${\mathcal R}$
. Then there is a countable set
${\mathcal R}$
. Then there is a countable set
![]() $C\subseteq PN^{(1)}_{{\mathcal R}}({\mathcal S})$
so that
$C\subseteq PN^{(1)}_{{\mathcal R}}({\mathcal S})$
so that
for almost every
![]() $x\in X$
.
$x\in X$
.
Proof. By [Reference Feldman, Sutherland and Zimmer15, Theorem 2.2], we may find a countable set
![]() $D\subseteq \operatorname {End}_{{\mathcal R}}({\mathcal S})$
so that
$D\subseteq \operatorname {End}_{{\mathcal R}}({\mathcal S})$
so that
for almost every
![]() $x\in X$
. Fix a countable subgroup
$x\in X$
. Fix a countable subgroup
![]() $H\subseteq [{\mathcal S}]$
so that
$H\subseteq [{\mathcal S}]$
so that
![]() $[x]_{{\mathcal S}}=Hx$
for almost every
$[x]_{{\mathcal S}}=Hx$
for almost every
![]() $x\in X$
. Then for almost every
$x\in X$
. Then for almost every
![]() $x\in X$
we have that
$x\in X$
we have that
 $$ \begin{align*}[x]_{{\mathcal R}}=\bigcup_{\phi\in D,\psi\in H}(\psi\circ \phi)(x).\end{align*} $$
$$ \begin{align*}[x]_{{\mathcal R}}=\bigcup_{\phi\in D,\psi\in H}(\psi\circ \phi)(x).\end{align*} $$
Fix a countable subgroup
![]() $G\subseteq [{\mathcal R}]$
so that
$G\subseteq [{\mathcal R}]$
so that
![]() $[x]_{{\mathcal R}}=Gx$
for almost every
$[x]_{{\mathcal R}}=Gx$
for almost every
![]() $x\in X$
. Then for each
$x\in X$
. Then for each
![]() $\phi \in D$
we may write, up to sets of measure zero,
$\phi \in D$
we may write, up to sets of measure zero,
 $$ \begin{align*}\operatorname{dom}(\phi)=\bigcup_{g\in G}E_{g,\phi}\end{align*} $$
$$ \begin{align*}\operatorname{dom}(\phi)=\bigcup_{g\in G}E_{g,\phi}\end{align*} $$
where
![]() $E_{g,\phi }\subseteq \{x\in \operatorname {dom}(\phi ):\phi (x)\in gx\}$
. For each
$E_{g,\phi }\subseteq \{x\in \operatorname {dom}(\phi ):\phi (x)\in gx\}$
. For each
![]() $g\in G$
,
$g\in G$
,
![]() $\phi \in D$
, define
$\phi \in D$
, define
![]() $\phi _{g}\in [[{\mathcal R}]]$
by declaring that
$\phi _{g}\in [[{\mathcal R}]]$
by declaring that
![]() $\operatorname {dom}(\phi _{g})=E_{g,\phi }$
and that
$\operatorname {dom}(\phi _{g})=E_{g,\phi }$
and that
![]() $\phi _{g}(x)=gx$
for
$\phi _{g}(x)=gx$
for
![]() $x\in E_{g,\phi }$
. Observe that
$x\in E_{g,\phi }$
. Observe that
![]() ${\phi _{g}\in PN^{(1)}_{{\mathcal R}}({\mathcal S})}$
. Then
${\phi _{g}\in PN^{(1)}_{{\mathcal R}}({\mathcal S})}$
. Then
 $$ \begin{align*}[x]_{{\mathcal R}}=\bigcup_{\substack{\psi\in H,\\ \phi\in D,g\in G \text{ with } x\in E_{g,\phi}}}\psi\circ \phi_{g}(x).\end{align*} $$
$$ \begin{align*}[x]_{{\mathcal R}}=\bigcup_{\substack{\psi\in H,\\ \phi\in D,g\in G \text{ with } x\in E_{g,\phi}}}\psi\circ \phi_{g}(x).\end{align*} $$
Thus,
is the desired countable set.
By the preceding lemma and the inclusion
![]() $[{\mathcal S}]\subseteq PN^{(1)}_{{\mathcal R}}({\mathcal S})$
, the condition that
$[{\mathcal S}]\subseteq PN^{(1)}_{{\mathcal R}}({\mathcal S})$
, the condition that
![]() $PN^{(1)}_{{\mathcal R}}({\mathcal S})$
acts ergodically on
$PN^{(1)}_{{\mathcal R}}({\mathcal S})$
acts ergodically on
![]() $(X,\mu )$
is satisfied if either
$(X,\mu )$
is satisfied if either
![]() ${\mathcal S}$
is ergodic or
${\mathcal S}$
is ergodic or
![]() ${\mathcal S}$
is normal and
${\mathcal S}$
is normal and
![]() ${\mathcal R}$
is ergodic. We will show that
${\mathcal R}$
is ergodic. We will show that
![]() $\rho ^{{\mathcal S}}$
is almost surely invariant under the partial one-sided normalizers, and is thus essentially constant when
$\rho ^{{\mathcal S}}$
is almost surely invariant under the partial one-sided normalizers, and is thus essentially constant when
![]() $PN^{(1)}_{{\mathcal R}}({\mathcal S})$
acts ergodically.
$PN^{(1)}_{{\mathcal R}}({\mathcal S})$
acts ergodically.
Since the elements of
![]() $PN^{(1)}_{{\mathcal R}}({\mathcal S})$
are only partially defined, we will need to relate the co-spectral radius to the modification given by Example 3.10 by restricting to a subset. It will not be hard to show from Theorem 3.7 that
$PN^{(1)}_{{\mathcal R}}({\mathcal S})$
are only partially defined, we will need to relate the co-spectral radius to the modification given by Example 3.10 by restricting to a subset. It will not be hard to show from Theorem 3.7 that
![]() $\rho _{E}^{{\mathcal S}}(x)$
as defined in Example 3.10 exists for almost every
$\rho _{E}^{{\mathcal S}}(x)$
as defined in Example 3.10 exists for almost every
![]() $x\in X$
. To deduce the existence of
$x\in X$
. To deduce the existence of
![]() $\rho ^{{\mathcal S}}_{E}(x)$
for almost every
$\rho ^{{\mathcal S}}_{E}(x)$
for almost every
![]() $x\in X$
, as well as some of its basic properties, we need to recall the
$x\in X$
, as well as some of its basic properties, we need to recall the
![]() ${\mathcal S}$
-saturation of a measurable set. Given a discrete, measure-preserving equivalence relation
${\mathcal S}$
-saturation of a measurable set. Given a discrete, measure-preserving equivalence relation
![]() ${\mathcal S}$
on a standard probability space and a measurable
${\mathcal S}$
on a standard probability space and a measurable
![]() $E\subseteq X$
, the
$E\subseteq X$
, the
![]() ${\mathcal S}$
-saturation of E is the (unique up to measure zero sets) measurable subset
${\mathcal S}$
-saturation of E is the (unique up to measure zero sets) measurable subset
![]() $\widetilde {E}\subseteq X$
satisfying the following properties:
$\widetilde {E}\subseteq X$
satisfying the following properties:
-
•
 $E\subseteq \widetilde {E}$
;
$E\subseteq \widetilde {E}$
; -
• for almost every
 $x\in \widetilde {E}$
we have
$x\in \widetilde {E}$
we have
 $[x]_{{\mathcal S}}\subseteq \widetilde {E}$
;
$[x]_{{\mathcal S}}\subseteq \widetilde {E}$
; -
• for almost every
 $x\in \widetilde {E}$
, there is a
$x\in \widetilde {E}$
, there is a
 $y\in E$
with
$y\in E$
with
 $x\in [y]_{{\mathcal S}}$
.
$x\in [y]_{{\mathcal S}}$
.
If
![]() $\Gamma \leq [{\mathcal S}]$
is a countable subgroup which generates
$\Gamma \leq [{\mathcal S}]$
is a countable subgroup which generates
![]() ${\mathcal S}$
, then a model for
${\mathcal S}$
, then a model for
![]() $\widetilde {E}$
can be given by
$\widetilde {E}$
can be given by
It will also be helpful to relate
![]() $\rho ^{{\mathcal S}}_{E}$
to a quantity more operator-theoretic in nature. For a measurable set
$\rho ^{{\mathcal S}}_{E}$
to a quantity more operator-theoretic in nature. For a measurable set
![]() $E\subseteq X$
of positive measure, and
$E\subseteq X$
of positive measure, and
![]() $x\in X$
, we let
$x\in X$
, we let
 $$ \begin{align*}p_{2k,x,{\mathcal S},E}=\sum_{y\in [x]_{{\mathcal S}}\cap E}p_{2k,x,y}.\end{align*} $$
$$ \begin{align*}p_{2k,x,{\mathcal S},E}=\sum_{y\in [x]_{{\mathcal S}}\cap E}p_{2k,x,y}.\end{align*} $$
We also let
 $$ \begin{align*}\rho_{E}({\mathcal R}/{\mathcal S},\nu)=\lim_{k\to\infty}\bigg(\frac{1}{\mu(E)}\int_{E}p_{2k,x,{\mathcal S},E}\,d\mu(x)\bigg)^{1/2k}.\end{align*} $$
$$ \begin{align*}\rho_{E}({\mathcal R}/{\mathcal S},\nu)=\lim_{k\to\infty}\bigg(\frac{1}{\mu(E)}\int_{E}p_{2k,x,{\mathcal S},E}\,d\mu(x)\bigg)^{1/2k}.\end{align*} $$
Define
![]() $\zeta _{E}\in L^{2}({\mathcal R}/{\mathcal S})$
by
$\zeta _{E}\in L^{2}({\mathcal R}/{\mathcal S})$
by
![]() $(\zeta _{E})_{x}={1_{E}(x)}/{\sqrt {\mu (E)}}\delta _{[x]_{{\mathcal S}}}$
. Then
$(\zeta _{E})_{x}={1_{E}(x)}/{\sqrt {\mu (E)}}\delta _{[x]_{{\mathcal S}}}$
. Then
so it follows from the spectral theorem that the limit defining
![]() $\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
exists. We now proceed to show that
$\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
exists. We now proceed to show that
![]() $\lim _{k\to \infty }p_{2k,x,{\mathcal S},E}^{{1}/{2k}}$
exists.
$\lim _{k\to \infty }p_{2k,x,{\mathcal S},E}^{{1}/{2k}}$
exists.
Corollary 3.17. Let
![]() $(X,\mu )$
be a standard probability space, and let
$(X,\mu )$
be a standard probability space, and let
![]() ${\mathcal S}\leq {\mathcal R}$
be discrete, probability-measure-preserving equivalence relations defined over X. Let
${\mathcal S}\leq {\mathcal R}$
be discrete, probability-measure-preserving equivalence relations defined over X. Let
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
be symmetric, countably supported, and generate
$\nu \in \operatorname {Prob}([{\mathcal R}])$
be symmetric, countably supported, and generate
![]() ${\mathcal R}$
. Fix a measurable
${\mathcal R}$
. Fix a measurable
![]() $E\subseteq X$
with positive measure.
$E\subseteq X$
with positive measure.
-
(a) For almost every
 $x\in X$
we have that exists and is almost surely
$x\in X$
we have that exists and is almost surely $$ \begin{align*}\rho^{{\mathcal S}}_{E}(x)=\lim_{k\to\infty}p_{2k,x,{\mathcal S},E}^{1/2k}\end{align*} $$
$$ \begin{align*}\rho^{{\mathcal S}}_{E}(x)=\lim_{k\to\infty}p_{2k,x,{\mathcal S},E}^{1/2k}\end{align*} $$
 ${\mathcal S}$
-invariant.
${\mathcal S}$
-invariant.
-
(b)
 $\|\rho ^{{\mathcal S}}_{E}\|_{\infty }=\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
.
$\|\rho ^{{\mathcal S}}_{E}\|_{\infty }=\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
.
Proof. Note that the sequence of functions
![]() $f_{k}\colon E\to [0,\infty )$
given by
$f_{k}\colon E\to [0,\infty )$
given by
satisfies the hypothesis of Theorem 3.7 with
![]() ${\mathcal R}$
replaced by
${\mathcal R}$
replaced by
![]() ${\mathcal R}|_{E}$
. This proves that
${\mathcal R}|_{E}$
. This proves that
![]() $\rho ^{{\mathcal S}}_{E}(x)$
exists for almost every
$\rho ^{{\mathcal S}}_{E}(x)$
exists for almost every
![]() $x\in E$
. Since
$x\in E$
. Since
Theorem 3.7 also proves (b).
To prove that
![]() $\rho ^{{\mathcal S}}_{E}(x)$
exists for almost every x, let
$\rho ^{{\mathcal S}}_{E}(x)$
exists for almost every x, let
![]() $\widetilde {E}$
be the
$\widetilde {E}$
be the
![]() ${\mathcal S}$
-saturation of E. Note that
${\mathcal S}$
-saturation of E. Note that
![]() $\rho ^{{\mathcal S}}_{E}(x)=0$
for almost every
$\rho ^{{\mathcal S}}_{E}(x)=0$
for almost every
![]() $x\in \widetilde {E}^{c}$
. For almost every
$x\in \widetilde {E}^{c}$
. For almost every
![]() $x\in \widetilde {E}$
, we have that
$x\in \widetilde {E}$
, we have that
![]() $\rho ^{{\mathcal S}}_{E}(y)$
exists for all
$\rho ^{{\mathcal S}}_{E}(y)$
exists for all
![]() $y\in [x]_{{\mathcal S}}\cap E$
. Fix such an
$y\in [x]_{{\mathcal S}}\cap E$
. Fix such an
![]() $x\in \widetilde {E}$
, and let
$x\in \widetilde {E}$
, and let
![]() $y\in [x]_{{\mathcal S}}\cap E.$
Then there is an
$y\in [x]_{{\mathcal S}}\cap E.$
Then there is an
![]() $\ell \in {\mathbb N}$
with
$\ell \in {\mathbb N}$
with
![]() $p_{\ell ,x,y}>0$
. So for all
$p_{\ell ,x,y}>0$
. So for all
![]() $k\geq 2\ell $
,
$k\geq 2\ell $
,
 $$ \begin{align*}p_{2k,x,{\mathcal S},E}=\sum_{z\in [x]_{{\mathcal S}}\cap E}p_{2k,x,z}\geq p_{\ell,x,y}^{2}\sum_{z\in [x]_{{\mathcal S}}\cap E}p_{2(k-\ell),y,z}=p_{\ell,x,y}^{2}p_{2(k-\ell),y,{\mathcal S},E}. \end{align*} $$
$$ \begin{align*}p_{2k,x,{\mathcal S},E}=\sum_{z\in [x]_{{\mathcal S}}\cap E}p_{2k,x,z}\geq p_{\ell,x,y}^{2}\sum_{z\in [x]_{{\mathcal S}}\cap E}p_{2(k-\ell),y,z}=p_{\ell,x,y}^{2}p_{2(k-\ell),y,{\mathcal S},E}. \end{align*} $$
This shows that for almost every
![]() $x\in \widetilde {E}$
we have
$x\in \widetilde {E}$
we have
The proof that
is similar.
It will be helpful to study how
![]() $\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
varies as a function of E. We can embed measurable subsets (modulo null sets) of
$\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
varies as a function of E. We can embed measurable subsets (modulo null sets) of
![]() $(X,\mu )$
into
$(X,\mu )$
into
![]() $L^{1}(X,\mu )$
via identifying each set with its indicator function. We thus have a natural distance on measurable sets modulo null sets defined by
$L^{1}(X,\mu )$
via identifying each set with its indicator function. We thus have a natural distance on measurable sets modulo null sets defined by
We show that
![]() $\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
is semicontinuous as function of E. For later use, it will also be useful to know that
$\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
is semicontinuous as function of E. For later use, it will also be useful to know that
![]() $\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
as a function of
$\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
as a function of
![]() ${\mathcal S}$
. We now define a topology on subrelations of
${\mathcal S}$
. We now define a topology on subrelations of
![]() ${\mathcal R}$
making this precise.
${\mathcal R}$
making this precise.
For
![]() ${\mathcal R}$
a discrete, probability-measure-preserving equivalence relation on
${\mathcal R}$
a discrete, probability-measure-preserving equivalence relation on
![]() $(X,\mu )$
,
$(X,\mu )$
,
![]() $\phi \in [[{\mathcal R}]]$
, and
$\phi \in [[{\mathcal R}]]$
, and
![]() ${\mathcal S}\leq {\mathcal R}$
, set
${\mathcal S}\leq {\mathcal R}$
, set
For a given subrelation
![]() ${\mathcal S}\leq {\mathcal R}$
, a finite set
${\mathcal S}\leq {\mathcal R}$
, a finite set
![]() $\Omega \subseteq [[{\mathcal R}]]$
, and
$\Omega \subseteq [[{\mathcal R}]]$
, and
![]() $\varepsilon>0$
, let
$\varepsilon>0$
, let
![]() ${\mathcal O}_{\Omega ,\varepsilon }({\mathcal S})$
consist of all subrelations
${\mathcal O}_{\Omega ,\varepsilon }({\mathcal S})$
consist of all subrelations
![]() ${\mathcal S}'\leq {\mathcal R}$
such that
${\mathcal S}'\leq {\mathcal R}$
such that
We define a topology on subrelations of
![]() ${\mathcal R}$
(modulo null sets) by declaring that the family
${\mathcal R}$
(modulo null sets) by declaring that the family
![]() ${\mathcal O}_{\Omega ,\varepsilon }({\mathcal S})$
form a neighborhood basis of
${\mathcal O}_{\Omega ,\varepsilon }({\mathcal S})$
form a neighborhood basis of
![]() ${\mathcal S}$
. Suppose that I is countable, and that
${\mathcal S}$
. Suppose that I is countable, and that
![]() $\Phi =(\phi _{i})_{i\in I}$
in
$\Phi =(\phi _{i})_{i\in I}$
in
![]() $[[{\mathcal R}]]$
is such that
$[[{\mathcal R}]]$
is such that
![]() $[x]_{{\mathcal R}}=\{\phi _{i}(x):i\in I,x\in \operatorname {dom}(\phi _{i})\}$
for almost every
$[x]_{{\mathcal R}}=\{\phi _{i}(x):i\in I,x\in \operatorname {dom}(\phi _{i})\}$
for almost every
![]() $x\in X$
. In this case, given
$x\in X$
. In this case, given
![]() $(\alpha _{i})_{i\in I}\in (0,1]^{I}$
with
$(\alpha _{i})_{i\in I}\in (0,1]^{I}$
with
![]() $\sum _{i}\alpha _{i}=1$
, we can define a metric on subrelations of
$\sum _{i}\alpha _{i}=1$
, we can define a metric on subrelations of
![]() ${\mathcal R}$
by
${\mathcal R}$
by
It can be check that this metric induces the topology defined above (moreover, this metric is complete, though we will not need this). We now prove our promised semicontinuity.
Lemma 3.18. Let
![]() $(X,\mu )$
be a standard probability space and
$(X,\mu )$
be a standard probability space and
![]() ${\mathcal R}$
a discrete, measure- preserving equivalence relation defined over X. Let
${\mathcal R}$
a discrete, measure- preserving equivalence relation defined over X. Let
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
be symmetric, countably supported, and generate
$\nu \in \operatorname {Prob}([{\mathcal R}])$
be symmetric, countably supported, and generate
![]() ${\mathcal R}$
. The map
${\mathcal R}$
. The map
![]() $(E,{\mathcal S})\mapsto \rho _{E}({\mathcal R}/{\mathcal S},\nu )$
is lower semicontinuous (where the domain is all pairs of positive measure, measurable subsets E of X and subrelations
$(E,{\mathcal S})\mapsto \rho _{E}({\mathcal R}/{\mathcal S},\nu )$
is lower semicontinuous (where the domain is all pairs of positive measure, measurable subsets E of X and subrelations
![]() ${\mathcal S}$
of
${\mathcal S}$
of
![]() ${\mathcal R}$
).
${\mathcal R}$
).
Proof. From
and the spectral theorem, we have
 $$ \begin{align*}\rho_{E}({\mathcal R}/{\mathcal S},\nu)=\sup_{k}\bigg(\frac{1}{\mu(E)}\int_{E} p_{2k,x,{\mathcal S},E}\,d\mu(x)\bigg)^{1/2k}.\end{align*} $$
$$ \begin{align*}\rho_{E}({\mathcal R}/{\mathcal S},\nu)=\sup_{k}\bigg(\frac{1}{\mu(E)}\int_{E} p_{2k,x,{\mathcal S},E}\,d\mu(x)\bigg)^{1/2k}.\end{align*} $$
It thus suffices to prove that
is continuous. Let
![]() $\operatorname {id}_{E}\in [[{\mathcal R}]]$
be defined by
$\operatorname {id}_{E}\in [[{\mathcal R}]]$
be defined by
![]() $\operatorname {dom}(\operatorname {id}_{E})=E$
and
$\operatorname {dom}(\operatorname {id}_{E})=E$
and
![]() $\operatorname {id}_{E}(x)=x$
for every
$\operatorname {id}_{E}(x)=x$
for every
![]() $x\in E$
. Then
$x\in E$
. Then
![]() $ \int _{E} p_{2k,x,{\mathcal S},E}\,d\mu (x)$
can be rewritten as
$ \int _{E} p_{2k,x,{\mathcal S},E}\,d\mu (x)$
can be rewritten as
 $$ \begin{align*}\sum_{\phi\in \operatorname{supp}(\nu^{*2k})}\nu^{*2k}(\phi)\mu(E\cap F_{{\mathcal S},\operatorname{id}_{E}\phi}).\end{align*} $$
$$ \begin{align*}\sum_{\phi\in \operatorname{supp}(\nu^{*2k})}\nu^{*2k}(\phi)\mu(E\cap F_{{\mathcal S},\operatorname{id}_{E}\phi}).\end{align*} $$
Note that each term in this sum is a continuous as a function of
![]() $(E,{\mathcal S})$
. Since
$(E,{\mathcal S})$
. Since
![]() $\sum _{\phi \in \operatorname {supp}(\nu ^{*2k})}\nu ^{*2k}(\phi )=1,$
it follows that the sum converges uniformly. Thus,
$\sum _{\phi \in \operatorname {supp}(\nu ^{*2k})}\nu ^{*2k}(\phi )=1,$
it follows that the sum converges uniformly. Thus,
is continuous.
For technical reasons, in order to show that
![]() $\rho ^{{\mathcal S}}$
is invariant under the partial normalizer of
$\rho ^{{\mathcal S}}$
is invariant under the partial normalizer of
![]() ${\mathcal S}$
inside of
${\mathcal S}$
inside of
![]() ${\mathcal R}$
, it will be helpful to reduce to the case that
${\mathcal R}$
, it will be helpful to reduce to the case that
![]() $\nu $
is lazy. We will briefly need to adopt notation for how the co-spectral radius depends upon the measure. So for
$\nu $
is lazy. We will briefly need to adopt notation for how the co-spectral radius depends upon the measure. So for
![]() ${\mathcal S}\leq {\mathcal R},X$
as in Theorem 3.20 and a countably supported
${\mathcal S}\leq {\mathcal R},X$
as in Theorem 3.20 and a countably supported
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
, we use
$\nu \in \operatorname {Prob}([{\mathcal R}])$
, we use
![]() $\rho ^{{\mathcal S}}_{\nu }(x)$
for the co-spectral radius at x defined using
$\rho ^{{\mathcal S}}_{\nu }(x)$
for the co-spectral radius at x defined using
![]() $\nu $
. Similarly, for
$\nu $
. Similarly, for
![]() $n\in {\mathbb N}$
we use
$n\in {\mathbb N}$
we use
![]() $p_{n,x,{\mathcal S}}^{\nu }$
for the probability that the random walk starting at x associated to
$p_{n,x,{\mathcal S}}^{\nu }$
for the probability that the random walk starting at x associated to
![]() $\nu $
is in
$\nu $
is in
![]() $[x]_{{\mathcal S}}$
after n steps.
$[x]_{{\mathcal S}}$
after n steps.
It will be helpful to use the following lemma which shows that the local co-spectral radius associated to
![]() $\nu $
is uniformly close to the local co-spectral radius associated to
$\nu $
is uniformly close to the local co-spectral radius associated to
![]() ${(1-t)\nu +t\delta _{\operatorname {id}}}$
as
${(1-t)\nu +t\delta _{\operatorname {id}}}$
as
![]() $t\to 0$
.
$t\to 0$
.
Lemma 3.19. Let
![]() $(X,\mu )$
be a standard probability space, and
$(X,\mu )$
be a standard probability space, and
![]() ${\mathcal S}\leq {\mathcal R}$
discrete, probability-measure-preserving equivalence relations defined over X. For a symmetric and countably supported
${\mathcal S}\leq {\mathcal R}$
discrete, probability-measure-preserving equivalence relations defined over X. For a symmetric and countably supported
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
and
$\nu \in \operatorname {Prob}([{\mathcal R}])$
and
![]() $t\in [0,1]$
, define
$t\in [0,1]$
, define
![]() $\nu _{t}=(1-t)\nu +t\delta _{\operatorname {id}}$
. Then
$\nu _{t}=(1-t)\nu +t\delta _{\operatorname {id}}$
. Then
Proof. To simplify notation, set
![]() $\rho =\rho ({\mathcal R}/{\mathcal S},\nu )$
. Let
$\rho =\rho ({\mathcal R}/{\mathcal S},\nu )$
. Let
![]() $\zeta _{E}$
be defined as in the discussion preceding Corollary 3.17. Let
$\zeta _{E}$
be defined as in the discussion preceding Corollary 3.17. Let
![]() $\eta \in \operatorname {Prob}([-\rho ,\rho ])$
be the spectral measure of
$\eta \in \operatorname {Prob}([-\rho ,\rho ])$
be the spectral measure of
![]() $\unicode{x3bb} (\nu )$
with respect to
$\unicode{x3bb} (\nu )$
with respect to
![]() $\zeta _{E}$
. Then for every measurable set
$\zeta _{E}$
. Then for every measurable set
![]() $E\subseteq X$
of positive measure we have that
$E\subseteq X$
of positive measure we have that
![]() $\rho _{E}({\mathcal R}/{\mathcal S},\nu _{t}),\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
are the
$\rho _{E}({\mathcal R}/{\mathcal S},\nu _{t}),\rho _{E}({\mathcal R}/{\mathcal S},\nu )$
are the
![]() $L^{\infty }$
-norms of
$L^{\infty }$
-norms of
![]() $s\mapsto s$
,
$s\mapsto s$
,
![]() $s\mapsto (1-t)s+t$
with respect to
$s\mapsto (1-t)s+t$
with respect to
![]() $\eta $
. In particular, for all measurable
$\eta $
. In particular, for all measurable
![]() $E\subseteq X$
of positive measure,
$E\subseteq X$
of positive measure,
If E is almost surely
![]() ${\mathcal S}$
-invariant, then
${\mathcal S}$
-invariant, then
![]() $\rho ^{{\mathcal S}}_{E}=\rho ^{{\mathcal S}}1_{E}$
. So Corollary 3.17(b) implies that
$\rho ^{{\mathcal S}}_{E}=\rho ^{{\mathcal S}}1_{E}$
. So Corollary 3.17(b) implies that
To prove the lemma, fix
![]() $c>0$
and let
$c>0$
and let
Note that E is
![]() ${\mathcal S}$
-invariant, by
${\mathcal S}$
-invariant, by
![]() ${\mathcal S}$
-invariance of
${\mathcal S}$
-invariance of
![]() $\rho ^{{\mathcal S}}_{\nu }$
and
$\rho ^{{\mathcal S}}_{\nu }$
and
![]() $\rho ^{{\mathcal S}}_{\nu _{t}}$
. Assume, for the sake of contradiction, that
$\rho ^{{\mathcal S}}_{\nu _{t}}$
. Assume, for the sake of contradiction, that
![]() $\mu (E)>0$
. Then by the preceding paragraph we have
$\mu (E)>0$
. Then by the preceding paragraph we have
On the other hand, the definition of E forces
Since
![]() $c>1$
, we obtain a contradiction. Thus,
$c>1$
, we obtain a contradiction. Thus,
almost everywhere. A similar proof shows that
![]() $\rho ^{{\mathcal S}}_{\nu }-\rho ^{{\mathcal S}}_{\nu _{t}}\leq ct(1+\rho )$
almost everywhere. Thus,
$\rho ^{{\mathcal S}}_{\nu }-\rho ^{{\mathcal S}}_{\nu _{t}}\leq ct(1+\rho )$
almost everywhere. Thus,
for all
![]() $c>1$
, and the proof is completed by letting
$c>1$
, and the proof is completed by letting
![]() $c\to 1$
.
$c\to 1$
.
The above reduction to the lazy case and the semicontinuity in Lemma 3.18 allow us to give a general formula for the local co-spectral radius in terms of the co-spectral radius. We will ultimately use this to prove invariance under partial normalizers of
![]() ${\mathcal S}\leq {\mathcal R}$
by restrict to sets where we have uniform lower bound on transition probabilities
${\mathcal S}\leq {\mathcal R}$
by restrict to sets where we have uniform lower bound on transition probabilities
![]() $p_{k,x,\phi (x)}$
for
$p_{k,x,\phi (x)}$
for
![]() $\phi \in PN^{(1)}_{{\mathcal R}}({\mathcal S})$
.
$\phi \in PN^{(1)}_{{\mathcal R}}({\mathcal S})$
.
Theorem 3.20. Let
![]() $(X,\mu )$
be a standard probability space, and let
$(X,\mu )$
be a standard probability space, and let
![]() ${\mathcal S}\leq {\mathcal R}$
be discrete, probability-measure-preserving equivalence relations defined over X, and fix a symmetric and countably supported
${\mathcal S}\leq {\mathcal R}$
be discrete, probability-measure-preserving equivalence relations defined over X, and fix a symmetric and countably supported
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
. If
$\nu \in \operatorname {Prob}([{\mathcal R}])$
. If
![]() $E\subseteq X$
has positive measure, then
$E\subseteq X$
has positive measure, then
where
![]() $\widetilde {E}$
is the
$\widetilde {E}$
is the
![]() ${\mathcal S}$
-saturation of E.
${\mathcal S}$
-saturation of E.
Proof. By Lemma 3.19, we may assume that
![]() $\nu $
is lazy. Observe that by
$\nu $
is lazy. Observe that by
![]() ${\mathcal S}$
-invariance of
${\mathcal S}$
-invariance of
![]() $\widetilde {E}$
, we have that
$\widetilde {E}$
, we have that
![]() $\rho ^{{\mathcal S}}1_{\widetilde {E}}=\rho ^{{\mathcal S}}_{\widetilde {E}}$
almost everywhere. Hence, it is enough to show that
$\rho ^{{\mathcal S}}1_{\widetilde {E}}=\rho ^{{\mathcal S}}_{\widetilde {E}}$
almost everywhere. Hence, it is enough to show that
![]() $\rho ^{{\mathcal S}}_{E}=\rho ^{{\mathcal S}}_{\widetilde {E}}$
almost everywhere. Clearly
$\rho ^{{\mathcal S}}_{E}=\rho ^{{\mathcal S}}_{\widetilde {E}}$
almost everywhere. Clearly
![]() $\rho ^{{\mathcal S}}_{E}\leq \rho ^{{\mathcal S}}_{\widetilde {E}}$
so it suffices to show that reverse inequality holds almost everywhere. For
$\rho ^{{\mathcal S}}_{E}\leq \rho ^{{\mathcal S}}_{\widetilde {E}}$
so it suffices to show that reverse inequality holds almost everywhere. For
![]() $k\in {\mathbb N}$
, let
$k\in {\mathbb N}$
, let
Then
![]() $E_{k}$
is an increasing sequence of sets with
$E_{k}$
is an increasing sequence of sets with
![]() $E_{k}\supseteq E$
. By symmetry and laziness of
$E_{k}\supseteq E$
. By symmetry and laziness of
![]() $\nu $
we know that
$\nu $
we know that
![]() $\bigcup _{k}E_{k}=\widetilde {E}$
up to sets of measure zero. By Lemma 3.18, it suffices to show that for almost every
$\bigcup _{k}E_{k}=\widetilde {E}$
up to sets of measure zero. By Lemma 3.18, it suffices to show that for almost every
![]() $k\in {\mathbb N}$
we have that
$k\in {\mathbb N}$
we have that
![]() $\rho ^{{\mathcal S}}_{E_{k}}\leq \rho ^{{\mathcal S}}_{E}$
almost surely.
$\rho ^{{\mathcal S}}_{E_{k}}\leq \rho ^{{\mathcal S}}_{E}$
almost surely.
For
![]() $m\in {\mathbb N}$
, set
$m\in {\mathbb N}$
, set
![]() $E_{k,m}=\{x\in X:p_{2k,x,{\mathcal S},E}>1/m\}$
. Then the
$E_{k,m}=\{x\in X:p_{2k,x,{\mathcal S},E}>1/m\}$
. Then the
![]() $E_{k,m}$
are increasing and
$E_{k,m}$
are increasing and
 $$ \begin{align*}E_{k}=\bigcup_{m=1}^{\infty}E_{k,m},\end{align*} $$
$$ \begin{align*}E_{k}=\bigcup_{m=1}^{\infty}E_{k,m},\end{align*} $$
so again by Lemma 3.18 it suffices to show that
![]() $\rho ^{{\mathcal S}}_{E_{k,m}}\leq \rho ^{{\mathcal S}}_{E}$
almost surely. Fix an
$\rho ^{{\mathcal S}}_{E_{k,m}}\leq \rho ^{{\mathcal S}}_{E}$
almost surely. Fix an
![]() $x\in E_{k,m}$
so that both
$x\in E_{k,m}$
so that both
![]() $\rho ^{{\mathcal S}}_{E}(x),\rho ^{{\mathcal S}}_{E_{k,m}}(x)$
exist. Then for every
$\rho ^{{\mathcal S}}_{E}(x),\rho ^{{\mathcal S}}_{E_{k,m}}(x)$
exist. Then for every
![]() $l\in {\mathbb N}$
,
$l\in {\mathbb N}$
,
 $$ \begin{align*}p_{2(l+k),x,{\mathcal S},E}\geq \sum_{y\in [x]_{{\mathcal S}}\cap E_{k,m}}p_{2l,x,y}p_{2k,y,{\mathcal S},E}\geq \frac{1}{m}p_{2l,x,{\mathcal S},E_{k,m}}.\end{align*} $$
$$ \begin{align*}p_{2(l+k),x,{\mathcal S},E}\geq \sum_{y\in [x]_{{\mathcal S}}\cap E_{k,m}}p_{2l,x,y}p_{2k,y,{\mathcal S},E}\geq \frac{1}{m}p_{2l,x,{\mathcal S},E_{k,m}}.\end{align*} $$
Taking
![]() $2l$
th roots of both sides and letting
$2l$
th roots of both sides and letting
![]() $l\to \infty $
shows that
$l\to \infty $
shows that
Since
![]() $\rho ^{{\mathcal S}}_{E},\rho ^{{\mathcal S}}_{E_{k,m}}$
exist almost everywhere, this completes the proof.
$\rho ^{{\mathcal S}}_{E},\rho ^{{\mathcal S}}_{E_{k,m}}$
exist almost everywhere, this completes the proof.
We now have amassed enough results to show that the co-spectral radius does not increase after applying partial normalizing elements.
Proposition 3.21. Let
![]() $(X,\mu )$
be a standard probability space, let
$(X,\mu )$
be a standard probability space, let
![]() ${\mathcal S}\leq {\mathcal R}$
be discrete, probability-measure-preserving equivalence relations defined over X, and fix a symmetric countably supported
${\mathcal S}\leq {\mathcal R}$
be discrete, probability-measure-preserving equivalence relations defined over X, and fix a symmetric countably supported
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
which generates
$\nu \in \operatorname {Prob}([{\mathcal R}])$
which generates
![]() ${\mathcal R}$
. Then for every
${\mathcal R}$
. Then for every
![]() $\phi \in PN^{(1)}_{{\mathcal R}}({\mathcal S})$
we have
$\phi \in PN^{(1)}_{{\mathcal R}}({\mathcal S})$
we have
for almost every
![]() $x\in \operatorname {dom}(\phi )$
.
$x\in \operatorname {dom}(\phi )$
.
Proof. First assume that
![]() $\nu $
is lazy. Fix
$\nu $
is lazy. Fix
![]() $\phi \in PN^{(1)}_{{\mathcal R}}({\mathcal S})$
. Replacing X with a co-null set, we may assume that
$\phi \in PN^{(1)}_{{\mathcal R}}({\mathcal S})$
. Replacing X with a co-null set, we may assume that
![]() $\phi ([x]_{{\mathcal S}}\cap \operatorname {dom}(\phi ))\subseteq [\phi (x)]_{{\mathcal S}}$
for every
$\phi ([x]_{{\mathcal S}}\cap \operatorname {dom}(\phi ))\subseteq [\phi (x)]_{{\mathcal S}}$
for every
![]() $x\in X$
. Since
$x\in X$
. Since
![]() $\nu $
is lazy and generating, for almost every
$\nu $
is lazy and generating, for almost every
![]() $x\in \operatorname {dom}(\phi )$
we have that
$x\in \operatorname {dom}(\phi )$
we have that
![]() $p_{k,x,\phi (x)}>0$
for all large k. So, up to sets of measure zero,
$p_{k,x,\phi (x)}>0$
for all large k. So, up to sets of measure zero,
 $$ \begin{align*}\operatorname{dom}(\phi)=\bigcup_{k=1}^{\infty}\{x\in \operatorname{dom}(\phi):p_{k,x,\phi(x)}>0\text{ for all } k\geq n\}.\end{align*} $$
$$ \begin{align*}\operatorname{dom}(\phi)=\bigcup_{k=1}^{\infty}\{x\in \operatorname{dom}(\phi):p_{k,x,\phi(x)}>0\text{ for all } k\geq n\}.\end{align*} $$
Since
![]() $\nu $
is lazy, this union is increasing and thus it follows that we may find a sequence
$\nu $
is lazy, this union is increasing and thus it follows that we may find a sequence
![]() $\delta _{n}\to 0$
of positive numbers and an increasing sequence of integers
$\delta _{n}\to 0$
of positive numbers and an increasing sequence of integers
![]() $r_{n}$
so that
$r_{n}$
so that
 $$ \begin{align*}\sum_{n=1}^{\infty}\mu(\{x\in \operatorname{dom}(\phi):p_{r_{n},x,\phi(x)}\leq \delta_{n}\})<\infty.\end{align*} $$
$$ \begin{align*}\sum_{n=1}^{\infty}\mu(\{x\in \operatorname{dom}(\phi):p_{r_{n},x,\phi(x)}\leq \delta_{n}\})<\infty.\end{align*} $$
Set
![]() $F_{n}=\{x\in \operatorname {dom}(\phi ):p_{r_{n},x,\phi (x)}>\delta _{n}\}$
and
$F_{n}=\{x\in \operatorname {dom}(\phi ):p_{r_{n},x,\phi (x)}>\delta _{n}\}$
and
![]() $E_{n}=\phi (F_{n}).$
By the Borel–Cantelli lemma, for almost every
$E_{n}=\phi (F_{n}).$
By the Borel–Cantelli lemma, for almost every
![]() $x\in \operatorname {dom}(\phi )$
we have that
$x\in \operatorname {dom}(\phi )$
we have that
![]() $x\in F_{k}$
for all sufficiently large
$x\in F_{k}$
for all sufficiently large
![]() $k.$
By Theorem 3.20, for almost every
$k.$
By Theorem 3.20, for almost every
![]() $x\in \operatorname {dom}(\phi )$
the following conditions are satisfied for all sufficiently large k:
$x\in \operatorname {dom}(\phi )$
the following conditions are satisfied for all sufficiently large k:
-
•
 $x\in F_{k}$
;
$x\in F_{k}$
; -
•
 $\rho ^{{\mathcal S}}(\phi (x))=\rho ^{{\mathcal S}}_{E_{k}}(\phi (x))$
;
$\rho ^{{\mathcal S}}(\phi (x))=\rho ^{{\mathcal S}}_{E_{k}}(\phi (x))$
; -
•
 $\rho ^{{\mathcal S}}(x)=\rho ^{{\mathcal S}}_{F_{k}}(x)$
.
$\rho ^{{\mathcal S}}(x)=\rho ^{{\mathcal S}}_{F_{k}}(x)$
.
Fix an
![]() $x\in \operatorname {dom}(\phi )$
which satisfies the above three conditions, and fix k such that the above three bulleted items hold. Then for all
$x\in \operatorname {dom}(\phi )$
which satisfies the above three conditions, and fix k such that the above three bulleted items hold. Then for all
![]() $l\in {\mathbb N}$
,
$l\in {\mathbb N}$
,
 $$ \begin{align*}p_{2l,\phi(x),{\mathcal S},E_{k}}=\sum_{z\in [\phi(x)]_{S}\cap E_{k}}p_{2l,\phi(x),z}.\end{align*} $$
$$ \begin{align*}p_{2l,\phi(x),{\mathcal S},E_{k}}=\sum_{z\in [\phi(x)]_{S}\cap E_{k}}p_{2l,\phi(x),z}.\end{align*} $$
Since
![]() $\phi ([x]_{{\mathcal S}}\cap \operatorname {dom}(\phi ))\subseteq [\phi (x)]_{{\mathcal S}}$
, and
$\phi ([x]_{{\mathcal S}}\cap \operatorname {dom}(\phi ))\subseteq [\phi (x)]_{{\mathcal S}}$
, and
![]() $\phi (x)\in E_{k},x\in F_{k}$
, we have for all
$\phi (x)\in E_{k},x\in F_{k}$
, we have for all
![]() $l\geq r_{k}$
that
$l\geq r_{k}$
that
 $$ \begin{align*}p_{2l,\phi(x),{\mathcal S},E_{k}}\geq \sum_{y\in [x]_{S}\cap F_{k}}p_{2l,\phi(x),\phi(y)}\geq \delta_{k}^{2}\sum_{y\in [x]_{S}\cap F_{k}}p_{2(l-r_{k}),x,y}=\delta_{k}^{2}p_{2(l-r_{k}),x,{\mathcal S},F_{k}},\end{align*} $$
$$ \begin{align*}p_{2l,\phi(x),{\mathcal S},E_{k}}\geq \sum_{y\in [x]_{S}\cap F_{k}}p_{2l,\phi(x),\phi(y)}\geq \delta_{k}^{2}\sum_{y\in [x]_{S}\cap F_{k}}p_{2(l-r_{k}),x,y}=\delta_{k}^{2}p_{2(l-r_{k}),x,{\mathcal S},F_{k}},\end{align*} $$
where in the second to last step we use symmetry and the fact that
![]() $x\in F_{k}$
. Thus,
$x\in F_{k}$
. Thus,
So
almost everywhere. The general case follows from the lazy case by using Lemma 3.19.
We are now ready to prove that the co-spectral radius does not change under the partial one-sided normalizers.
Corollary 3.22. Let
![]() $(X,\mu )$
be a standard probability space, let
$(X,\mu )$
be a standard probability space, let
![]() ${\mathcal S}\leq {\mathcal R}$
be discrete, probability-measure-preserving equivalence relations defined over X, and fix a symmetric and countably supported
${\mathcal S}\leq {\mathcal R}$
be discrete, probability-measure-preserving equivalence relations defined over X, and fix a symmetric and countably supported
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
which generates
$\nu \in \operatorname {Prob}([{\mathcal R}])$
which generates
![]() ${\mathcal R}$
. Suppose that
${\mathcal R}$
. Suppose that
![]() $PN^{(1)}_{{\mathcal R}}({\mathcal S})$
acts ergodically on
$PN^{(1)}_{{\mathcal R}}({\mathcal S})$
acts ergodically on
![]() $(X,\mu )$
. Then
$(X,\mu )$
. Then
![]() $\rho ^{{\mathcal S}}$
is almost surely constant (in particular, by Lemma 3.16 this applies if
$\rho ^{{\mathcal S}}$
is almost surely constant (in particular, by Lemma 3.16 this applies if
![]() ${\mathcal S}$
is normal in
${\mathcal S}$
is normal in
![]() ${\mathcal R}$
and
${\mathcal R}$
and
![]() ${\mathcal R}$
is ergodic).
${\mathcal R}$
is ergodic).
Proof. Let C be as in Lemma 3.16. By the preceding proposition and countability, for every
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
is invariant under C, and so by ergodicity of
![]() ${\mathcal R}$
has measure
${\mathcal R}$
has measure
![]() $0$
or
$0$
or
![]() $1$
for every
$1$
for every
![]() $t\in [0,1]$
. If
$t\in [0,1]$
. If
![]() $s=\sup \{t:\mu (E_{t})=1\}$
, then
$s=\sup \{t:\mu (E_{t})=1\}$
, then
![]() $\rho ^{{\mathcal S}}\geq s$
almost everywhere, and
$\rho ^{{\mathcal S}}\geq s$
almost everywhere, and
![]() $\rho ^{{\mathcal S}}(x)<s+{1}/{n}$
for almost every x and every
$\rho ^{{\mathcal S}}(x)<s+{1}/{n}$
for almost every x and every
![]() $n\in {\mathbb N}$
. Thus,
$n\in {\mathbb N}$
. Thus,
![]() $\rho ^{{\mathcal S}}(x)=s$
for almost every x.
$\rho ^{{\mathcal S}}(x)=s$
for almost every x.
We close this section with an example illustrating the fact that
![]() $\rho ^{{\mathcal S}}(x)$
may fail to be essentially constant if we only assume that
$\rho ^{{\mathcal S}}(x)$
may fail to be essentially constant if we only assume that
![]() ${\mathcal R}$
is ergodic. Thus, we need to assume something special about the inclusion
${\mathcal R}$
is ergodic. Thus, we need to assume something special about the inclusion
![]() ${\mathcal S}\leq {\mathcal R}$
.
${\mathcal S}\leq {\mathcal R}$
.
Example 3.23. Let
![]() ${\mathcal R}$
be an ergodic, discrete, measure-preserving equivalence relation on
${\mathcal R}$
be an ergodic, discrete, measure-preserving equivalence relation on
![]() $(X,\mu )$
. Let
$(X,\mu )$
. Let
![]() $E\subseteq X$
be a measurable set of positive measure. Let
$E\subseteq X$
be a measurable set of positive measure. Let
We claim that the following statements hold.
Claim
-
(i) For almost every
 $x\in E^{c}$
, we have
$x\in E^{c}$
, we have
 $\rho ^{{\mathcal S}}(x)=\rho ({\mathcal R},\nu )$
.
$\rho ^{{\mathcal S}}(x)=\rho ({\mathcal R},\nu )$
. -
(ii) For almost every
 $x\in E$
, we have
$x\in E$
, we have
 $\rho ^{{\mathcal S}}(x)=1.$
$\rho ^{{\mathcal S}}(x)=1.$
In particular, if
![]() ${\mathcal R}$
is not hyperfinite, then by [Reference Bowen, Hoff and Ioana10, Lemma 2.2.] there is a
${\mathcal R}$
is not hyperfinite, then by [Reference Bowen, Hoff and Ioana10, Lemma 2.2.] there is a
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
so that
$\nu \in \operatorname {Prob}([{\mathcal R}])$
so that
![]() $\rho ({\mathcal R},\nu )<1$
(this also follows from condition (GM) in [Reference Kaimanovich26] being equivalent to hyperfiniteness) and this gives an example where the co-spectral radius is not essentially constant.
$\rho ({\mathcal R},\nu )<1$
(this also follows from condition (GM) in [Reference Kaimanovich26] being equivalent to hyperfiniteness) and this gives an example where the co-spectral radius is not essentially constant.
Proof of claim
Let
![]() $\mathcal {T}=\{(x,x):x\in X\}$
. Let
$\mathcal {T}=\{(x,x):x\in X\}$
. Let
![]() $\unicode{x3bb} _{x}(\nu )$
be the Markov operator associated to
$\unicode{x3bb} _{x}(\nu )$
be the Markov operator associated to
![]() $\nu $
acting on
$\nu $
acting on
![]() $\ell ^{2}([x]_{{\mathcal R}})$
. Then for all
$\ell ^{2}([x]_{{\mathcal R}})$
. Then for all
![]() $x\in X$
we have
$x\in X$
we have
and so the co-spectral radius of
![]() ${\mathcal R}$
with respect to
${\mathcal R}$
with respect to
![]() ${\mathcal T}$
agrees with the spectral radius of
${\mathcal T}$
agrees with the spectral radius of
![]() $[x]_{{\mathcal R}}$
with respect to
$[x]_{{\mathcal R}}$
with respect to
![]() $\nu $
, that is,
$\nu $
, that is,
![]() $\rho ^{{\mathcal T}}(x)=\|\unicode{x3bb} _{x}(\nu )\|$
. If
$\rho ^{{\mathcal T}}(x)=\|\unicode{x3bb} _{x}(\nu )\|$
. If
![]() $(x,y)\in {\mathcal R}$
, then
$(x,y)\in {\mathcal R}$
, then
![]() $\unicode{x3bb} _{x}(\nu ),\unicode{x3bb} _{y}(\nu )$
are both operators on
$\unicode{x3bb} _{x}(\nu ),\unicode{x3bb} _{y}(\nu )$
are both operators on
![]() $\ell ^{2}([x]_{{\mathcal R}})$
and
$\ell ^{2}([x]_{{\mathcal R}})$
and
![]() $\unicode{x3bb} _{x}(\nu )=\unicode{x3bb} _{y}(\nu )$
. So, by ergodicity, the operator norm
$\unicode{x3bb} _{x}(\nu )=\unicode{x3bb} _{y}(\nu )$
. So, by ergodicity, the operator norm
![]() $\|\unicode{x3bb} _{x}(\nu )\|$
is essentially constant. Since
$\|\unicode{x3bb} _{x}(\nu )\|$
is essentially constant. Since
![]() $\rho ({\mathcal R}/{\mathcal T},\nu )=\rho ({\mathcal R},\nu )$
, it follows from Theorem 3.2(ii) that
$\rho ({\mathcal R}/{\mathcal T},\nu )=\rho ({\mathcal R},\nu )$
, it follows from Theorem 3.2(ii) that
![]() $\|\unicode{x3bb} _{x}(\nu )\|$
is almost surely equal to
$\|\unicode{x3bb} _{x}(\nu )\|$
is almost surely equal to
![]() $\rho ({\mathcal R},\nu )$
.
$\rho ({\mathcal R},\nu )$
.
(i) For almost every
![]() $x\in E^{c}$
we have
$x\in E^{c}$
we have
![]() $\rho ^{{\mathcal S}}(x)=\rho ^{{\mathcal T}}(x)$
, so this follows by the preceding paragraph.
$\rho ^{{\mathcal S}}(x)=\rho ^{{\mathcal T}}(x)$
, so this follows by the preceding paragraph.
(ii) For almost every
![]() $x\in E$
we have
$x\in E$
we have
![]() $\rho ^{{\mathcal S}}(x)=\rho _{E}^{{\mathcal R}}(x)$
, with notation as in Corollary 3.17. So this follows from Theorem 3.20.
$\rho ^{{\mathcal S}}(x)=\rho _{E}^{{\mathcal R}}(x)$
, with notation as in Corollary 3.17. So this follows from Theorem 3.20.
4. Co-spectral radius and hyperfinite subrelations
In this section we investigate the relation between co-spectral radius and hyperfiniteness. Specifically, we show that if
![]() ${\mathcal S}$
is hyperfinite, then
${\mathcal S}$
is hyperfinite, then
![]() $\rho ({\mathcal R}/{\mathcal S},\nu )=\rho ({\mathcal R},\nu )$
.
$\rho ({\mathcal R}/{\mathcal S},\nu )=\rho ({\mathcal R},\nu )$
.
Proposition 4.1. Let
![]() ${\mathcal R}$
be an ergodic, discrete measure-preserving equivalence relation over a standard probability space
${\mathcal R}$
be an ergodic, discrete measure-preserving equivalence relation over a standard probability space
![]() $(X,\mu ).$
Suppose that
$(X,\mu ).$
Suppose that
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
is countably supported, symmetric, and that
$\nu \in \operatorname {Prob}([{\mathcal R}])$
is countably supported, symmetric, and that
![]() $\mathcal {S}\leq {\mathcal R}$
is hyperfinite. Then
$\mathcal {S}\leq {\mathcal R}$
is hyperfinite. Then
![]() $\rho ({\mathcal R},\nu )=\rho ({\mathcal R}/\mathcal {S},\nu ).$
$\rho ({\mathcal R},\nu )=\rho ({\mathcal R}/\mathcal {S},\nu ).$
Proof. The inequality
![]() $\rho ({\mathcal R},\nu )\leq \rho ({\mathcal R}/\mathcal {S},\nu )$
is clear, so it remains to prove the reverse inequality. Since
$\rho ({\mathcal R},\nu )\leq \rho ({\mathcal R}/\mathcal {S},\nu )$
is clear, so it remains to prove the reverse inequality. Since
![]() $\mathcal {S}$
is hyperfinite, we can write
$\mathcal {S}$
is hyperfinite, we can write
![]() $\mathcal {S}=\bigcup _{n}\mathcal {S}_{n}$
, where
$\mathcal {S}=\bigcup _{n}\mathcal {S}_{n}$
, where
![]() $\mathcal {S}_{n}\leq {\mathcal R}$
is an increasing sequence and
$\mathcal {S}_{n}\leq {\mathcal R}$
is an increasing sequence and
![]() ${\mathcal S}_{n}$
is an equivalence relation where almost every equivalence class is finite. Note that
${\mathcal S}_{n}$
is an equivalence relation where almost every equivalence class is finite. Note that
![]() ${\mathcal S}_{n}$
converges to
${\mathcal S}_{n}$
converges to
![]() ${\mathcal S}$
in the topology defined by Lemma 3.18. Thus, by Lemma 3.18, it is enough to show that
${\mathcal S}$
in the topology defined by Lemma 3.18. Thus, by Lemma 3.18, it is enough to show that
![]() $\rho ({\mathcal R}/\mathcal {S}_{n},\nu )\leq \rho ({\mathcal R},\nu )$
for every
$\rho ({\mathcal R}/\mathcal {S}_{n},\nu )\leq \rho ({\mathcal R},\nu )$
for every
![]() $n\in {\mathbb N}.$
For an integer
$n\in {\mathbb N}.$
For an integer
![]() $\ell $
, let
$\ell $
, let
![]() $E_{\ell }=\{x\in X:|[x]_{{\mathcal S}_{n}}|\leq \ell \}$
. Then the
$E_{\ell }=\{x\in X:|[x]_{{\mathcal S}_{n}}|\leq \ell \}$
. Then the
![]() $E_{k}$
are an increasing sequence of measurable subsets whose union is co-null. By Theorem 3.2, we know that
$E_{k}$
are an increasing sequence of measurable subsets whose union is co-null. By Theorem 3.2, we know that
![]() $\rho ({\mathcal R}/{\mathcal S}_{n},\nu )=\|\rho ^{{\mathcal S}_{n}}\|_{\infty }$
. So it suffices to show that
$\rho ({\mathcal R}/{\mathcal S}_{n},\nu )=\|\rho ^{{\mathcal S}_{n}}\|_{\infty }$
. So it suffices to show that
![]() $\|\rho ^{{\mathcal S}_{n}}1_{E_{\ell }}\|_{\infty }\leq \rho ({\mathcal R},\nu )$
for all
$\|\rho ^{{\mathcal S}_{n}}1_{E_{\ell }}\|_{\infty }\leq \rho ({\mathcal R},\nu )$
for all
![]() $\ell ,n$
.
$\ell ,n$
.
Fix integer
![]() $n,\ell \in {\mathbb N}.$
We may then choose
$n,\ell \in {\mathbb N}.$
We may then choose
![]() $\phi _{1},\ldots ,\phi _{\ell }\in [[{\mathcal S}_{n}]]$
so that for every
$\phi _{1},\ldots ,\phi _{\ell }\in [[{\mathcal S}_{n}]]$
so that for every
![]() $x\in E_{\ell }$
,
$x\in E_{\ell }$
,
with
![]() $\phi _{1}=\operatorname {id}$
. Then, for every
$\phi _{1}=\operatorname {id}$
. Then, for every
![]() $x\in E_{\ell }$
, and every
$x\in E_{\ell }$
, and every
![]() $k\in {\mathbb N}$
,
$k\in {\mathbb N}$
,
 $$ \begin{align*}p_{2k,x,{\mathcal S}_{n}}=\sum_{j=1}^{\ell}p_{2k,x,\phi_{j}(x)}1_{\operatorname{dom}(\phi_{j})}(x).\end{align*} $$
$$ \begin{align*}p_{2k,x,{\mathcal S}_{n}}=\sum_{j=1}^{\ell}p_{2k,x,\phi_{j}(x)}1_{\operatorname{dom}(\phi_{j})}(x).\end{align*} $$
Set
Then
 $$ \begin{align*}\rho^{{\mathcal S}_{n}}(x)&=\lim_{k\to\infty}p_{2k,x,{\mathcal S}}^{1/2k}=\lim_{k\to\infty}\bigg(\sum_{j=1}^{\ell}p_{2k,x,\phi_{j}(x)}1_{\operatorname{dom}(\phi_{j})})(x)\bigg)^{1/2k}\\&=\lim_{k\to\infty}\max_{j}\bigg(p_{2k,x,\phi_{j}(x)}1_{\operatorname{dom}(\phi_{j})}\bigg)^{1/2k}.\end{align*} $$
$$ \begin{align*}\rho^{{\mathcal S}_{n}}(x)&=\lim_{k\to\infty}p_{2k,x,{\mathcal S}}^{1/2k}=\lim_{k\to\infty}\bigg(\sum_{j=1}^{\ell}p_{2k,x,\phi_{j}(x)}1_{\operatorname{dom}(\phi_{j})})(x)\bigg)^{1/2k}\\&=\lim_{k\to\infty}\max_{j}\bigg(p_{2k,x,\phi_{j}(x)}1_{\operatorname{dom}(\phi_{j})}\bigg)^{1/2k}.\end{align*} $$
For each
![]() $j\in \{0,\ldots ,\ell \}$
such that
$j\in \{0,\ldots ,\ell \}$
such that
![]() $x\in \operatorname {dom}(\phi _{j})$
, we may choose a non-negative integer
$x\in \operatorname {dom}(\phi _{j})$
, we may choose a non-negative integer
![]() $t_{j}$
so that
$t_{j}$
so that
![]() $p_{t_{j},x,\phi _{j}(x)}>0$
. Thus,
$p_{t_{j},x,\phi _{j}(x)}>0$
. Thus,
Thus,
for almost every x. Hence,
In the group context, the analogous statement is that if
![]() $\Gamma $
is a countable, discrete group and
$\Gamma $
is a countable, discrete group and
![]() $\nu \in \operatorname {Prob}(\Gamma )$
is symmetric with
$\nu \in \operatorname {Prob}(\Gamma )$
is symmetric with
![]() $\langle \operatorname {supp}(\nu ) \rangle =\Gamma $
, then for any amenable
$\langle \operatorname {supp}(\nu ) \rangle =\Gamma $
, then for any amenable
![]() $H\leq \Gamma $
we have that
$H\leq \Gamma $
we have that
![]() $\rho (\Gamma ,\nu )=\rho (\Gamma /H,\nu )$
. It is known that the converse fails, namely there are cases of
$\rho (\Gamma ,\nu )=\rho (\Gamma /H,\nu )$
. It is known that the converse fails, namely there are cases of
![]() $\Gamma ,\nu $
, and non-amenable
$\Gamma ,\nu $
, and non-amenable
![]() $H\leq \Gamma $
such that
$H\leq \Gamma $
such that
![]() $\rho (\Gamma ,\nu )=\rho (\Gamma /H,\nu )$
. It is a theorem of Kesten [Reference Kesten30, Theorem 2] that the converse is true if we assume in addition that H is normal. This was generalized to invariant random subgroups by Abért, Glasner, and Virág (see [Reference Abért, Glasner and Virág3]). Normal subgroups and invariant random subgroups can both be realized as a special case of normal subrelations. So it is natural to ask if
$\rho (\Gamma ,\nu )=\rho (\Gamma /H,\nu )$
. It is a theorem of Kesten [Reference Kesten30, Theorem 2] that the converse is true if we assume in addition that H is normal. This was generalized to invariant random subgroups by Abért, Glasner, and Virág (see [Reference Abért, Glasner and Virág3]). Normal subgroups and invariant random subgroups can both be realized as a special case of normal subrelations. So it is natural to ask if
![]() ${\mathcal R}$
is an ergodic, probability-measure-preserving, discrete relation, if
${\mathcal R}$
is an ergodic, probability-measure-preserving, discrete relation, if
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
is symmetric and generating, and if
$\nu \in \operatorname {Prob}([{\mathcal R}])$
is symmetric and generating, and if
![]() ${\mathcal S}\triangleleft {\mathcal R}$
has
${\mathcal S}\triangleleft {\mathcal R}$
has
![]() $\rho ({\mathcal R},\nu )=\rho ({\mathcal R}/{\mathcal S},\nu )$
, whether we necessarily have that
$\rho ({\mathcal R},\nu )=\rho ({\mathcal R}/{\mathcal S},\nu )$
, whether we necessarily have that
![]() ${\mathcal S}$
is hyperfinite?. We will show that the answer is negative in general, but it might be helpful first to study a special case.
${\mathcal S}$
is hyperfinite?. We will show that the answer is negative in general, but it might be helpful first to study a special case.
In general, a normal subrelation
![]() ${\mathcal S}\triangleleft {\mathcal R}$
can be expressed in terms of the partial one-sided normalizers of
${\mathcal S}\triangleleft {\mathcal R}$
can be expressed in terms of the partial one-sided normalizers of
![]() ${\mathcal S}$
generating
${\mathcal S}$
generating
![]() ${\mathcal R}$
(recall our discussion for §3.3). Let us begin by investigating the case when
${\mathcal R}$
(recall our discussion for §3.3). Let us begin by investigating the case when
![]() ${\mathcal R}$
is generated by
${\mathcal R}$
is generated by
![]() $N_{{\mathcal R}}({\mathcal S})=\{\phi \in [{\mathcal R}]:\phi ([x]_{{\mathcal S}})=[\phi (x)]_{{\mathcal S}}\text { for almost every} x\in X\}$
. Moreover, to simplify things, assume that
$N_{{\mathcal R}}({\mathcal S})=\{\phi \in [{\mathcal R}]:\phi ([x]_{{\mathcal S}})=[\phi (x)]_{{\mathcal S}}\text { for almost every} x\in X\}$
. Moreover, to simplify things, assume that
![]() $\nu $
is the uniform measure on a finite, generating subset
$\nu $
is the uniform measure on a finite, generating subset
![]() $\Phi $
of
$\Phi $
of
![]() $N_{{\mathcal R}}({\mathcal S})$
. It turns out that we can naturally translate this special case into a generalization of the Abért–Glasner–Virag result.
$N_{{\mathcal R}}({\mathcal S})$
. It turns out that we can naturally translate this special case into a generalization of the Abért–Glasner–Virag result.
Proposition 4.2. Let
![]() ${\mathcal R}$
be a discrete, ergodic, probability-measure-preserving equivalence relation over a standard probability space
${\mathcal R}$
be a discrete, ergodic, probability-measure-preserving equivalence relation over a standard probability space
![]() $(X,\mu )$
. Let
$(X,\mu )$
. Let
![]() ${\mathcal S}\leq {\mathcal R}$
, and let
${\mathcal S}\leq {\mathcal R}$
, and let
![]() $\Gamma \leq N_{{\mathcal R}}({\mathcal S})$
be a countable subgroup. For
$\Gamma \leq N_{{\mathcal R}}({\mathcal S})$
be a countable subgroup. For
![]() $x\in X$
, set
$x\in X$
, set
![]() $H_{x}=\{\phi \in \Gamma :\phi (x)\in [x]_{{\mathcal S}}\}$
.
$H_{x}=\{\phi \in \Gamma :\phi (x)\in [x]_{{\mathcal S}}\}$
.
-
(i) For almost every
 $x\in X$
, we have that
$x\in X$
, we have that
 $H_{x}$
is a subgroup of
$H_{x}$
is a subgroup of
 $\Gamma $
. Moreover, for almost every
$\Gamma $
. Moreover, for almost every
 $x\in X$
and every
$x\in X$
and every
 $\phi \in \Gamma $
we have
$\phi \in \Gamma $
we have
 $H_{\phi (x)}=\phi H_{x}\phi ^{-1}$
.
$H_{\phi (x)}=\phi H_{x}\phi ^{-1}$
. -
(ii) If
 $\,\Gamma $
generates
$\,\Gamma $
generates
 ${\mathcal R}$
, then for almost every
${\mathcal R}$
, then for almost every
 $x\in X$
we have that
$x\in X$
we have that
 $[x]_{{\mathcal S}}=H_{x}x$
.
$[x]_{{\mathcal S}}=H_{x}x$
. -
(iii) Suppose that
 $\Gamma $
generates
$\Gamma $
generates
 ${\mathcal R}$
, and that
${\mathcal R}$
, and that
 $\nu \in \operatorname {Prob}(\Gamma )$
is symmetric with
$\nu \in \operatorname {Prob}(\Gamma )$
is symmetric with
 ${\langle \operatorname {supp}(\nu ) \rangle =\Gamma }$
. Then for almost every
${\langle \operatorname {supp}(\nu ) \rangle =\Gamma }$
. Then for almost every
 $x\in X$
we have
$x\in X$
we have  $$ \begin{align*}\rho({\mathcal R},\nu)=\rho(\Gamma/\operatorname{Stab}_{\Gamma}(x),\nu),\,\,\, \rho({\mathcal R}/{\mathcal S},\nu)=\rho(\Gamma/H_{x},\nu).\end{align*} $$
$$ \begin{align*}\rho({\mathcal R},\nu)=\rho(\Gamma/\operatorname{Stab}_{\Gamma}(x),\nu),\,\,\, \rho({\mathcal R}/{\mathcal S},\nu)=\rho(\Gamma/H_{x},\nu).\end{align*} $$
Proof. Items (i) and (ii) follow from [Reference Tucker-Drob38, Proposition 8.10].
(iii) Since
![]() $\Gamma $
generates
$\Gamma $
generates
![]() ${\mathcal R}$
, for almost every
${\mathcal R}$
, for almost every
![]() $x\in X$
we have a
$x\in X$
we have a
![]() $\Gamma $
-equivariant bijection
$\Gamma $
-equivariant bijection
![]() $f\colon \Gamma /\operatorname {Stab}_{\Gamma }(x)\to [x]_{{\mathcal R}}$
satisfying
$f\colon \Gamma /\operatorname {Stab}_{\Gamma }(x)\to [x]_{{\mathcal R}}$
satisfying
![]() $f(\phi (x)\operatorname {Stab}_{\Gamma }(x))$
for every
$f(\phi (x)\operatorname {Stab}_{\Gamma }(x))$
for every
![]() $\phi \in \Gamma $
. Moreover, since
$\phi \in \Gamma $
. Moreover, since
![]() $\Gamma \leq N_{{\mathcal R}}({\mathcal S})$
, for almost every
$\Gamma \leq N_{{\mathcal R}}({\mathcal S})$
, for almost every
![]() $x\in X$
we have for all
$x\in X$
we have for all
![]() $\phi ,\psi \in \Gamma $
that
$\phi ,\psi \in \Gamma $
that
![]() $(\phi (x),\psi (x))\in {\mathcal S}$
if and only if
$(\phi (x),\psi (x))\in {\mathcal S}$
if and only if
![]() $(\psi ^{-1}\phi (x),x)\in {\mathcal S}$
, which is equivalent to saying that
$(\psi ^{-1}\phi (x),x)\in {\mathcal S}$
, which is equivalent to saying that
![]() $\phi H_{x}=\psi H_{x}$
. Thus, f induces a
$\phi H_{x}=\psi H_{x}$
. Thus, f induces a
![]() $\Gamma $
-equivariant bijection
$\Gamma $
-equivariant bijection
![]() $\overline {f}\colon \Gamma /H_{x}\to [x]_{{\mathcal R}}/{\mathcal S}$
satisfying
$\overline {f}\colon \Gamma /H_{x}\to [x]_{{\mathcal R}}/{\mathcal S}$
satisfying
![]() $\overline {f}(\phi H_{x})=[\phi (x)]_{{\mathcal S}}$
.
$\overline {f}(\phi H_{x})=[\phi (x)]_{{\mathcal S}}$
.
For
![]() $H\leq \Gamma $
, let
$H\leq \Gamma $
, let
![]() $p_{k,H}$
be the probability that the random walk on
$p_{k,H}$
be the probability that the random walk on
![]() $\Gamma $
corresponding to
$\Gamma $
corresponding to
![]() $\nu $
and starting at
$\nu $
and starting at
![]() $1$
is at H after k steps. Then by the above paragraph we have for almost every
$1$
is at H after k steps. Then by the above paragraph we have for almost every
![]() $x\in X$
that
$x\in X$
that
Thus, for almost every
![]() $x\in X$
, we have
$x\in X$
, we have
Since we are assuming that
![]() ${\mathcal R}$
is ergodic and that
${\mathcal R}$
is ergodic and that
![]() $\Gamma \leq N_{{\mathcal R}}({\mathcal S})$
generates
$\Gamma \leq N_{{\mathcal R}}({\mathcal S})$
generates
![]() ${\mathcal R}$
, the result now follows from Theorem 3.2(iii).
${\mathcal R}$
, the result now follows from Theorem 3.2(iii).
The above proposition motivates the following definition, which first appeared in [Reference Tucker-Drob38, §8] (under slightly different terminology). Recall that if
![]() $\Gamma $
is a countable, discrete group
$\Gamma $
is a countable, discrete group
![]() $\operatorname {Sub}(\Gamma )$
denotes the space of subgroups of
$\operatorname {Sub}(\Gamma )$
denotes the space of subgroups of
![]() $\Gamma $
. We may identify each subgroup with its indicator function and thus view
$\Gamma $
. We may identify each subgroup with its indicator function and thus view
![]() $\operatorname {Sub}(\Gamma )\subseteq \{0,1\}^{\Gamma }$
. We may thus regard
$\operatorname {Sub}(\Gamma )\subseteq \{0,1\}^{\Gamma }$
. We may thus regard
![]() $\operatorname {Sub}(\Gamma )$
as a compact, metrizable space by giving
$\operatorname {Sub}(\Gamma )$
as a compact, metrizable space by giving
![]() $\operatorname {Sub}(\Gamma )$
the restriction of the product topology. An invariant random subgroup is a Borel probability measure
$\operatorname {Sub}(\Gamma )$
the restriction of the product topology. An invariant random subgroup is a Borel probability measure
![]() $\eta $
on
$\eta $
on
![]() $\operatorname {Sub}(\Gamma )$
which is invariant under the conjugation action of
$\operatorname {Sub}(\Gamma )$
which is invariant under the conjugation action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\operatorname {Sub}(\Gamma )$
. We let
$\operatorname {Sub}(\Gamma )$
. We let
![]() $\operatorname {IRS}(\Gamma )$
be the space of invariant random subgroups of
$\operatorname {IRS}(\Gamma )$
be the space of invariant random subgroups of
![]() $\Gamma $
.
$\Gamma $
.
Definition 4.3. (§8 of [Reference Tucker-Drob38])
Suppose that
![]() $\eta _{1},\eta _{2}\in \operatorname {IRS}(\Gamma )$
. A monotone joining of
$\eta _{1},\eta _{2}\in \operatorname {IRS}(\Gamma )$
. A monotone joining of
![]() $\eta _{1}$
with
$\eta _{1}$
with
![]() $\eta _{2}$
is a
$\eta _{2}$
is a
![]() $\zeta \in \operatorname {Prob}(\operatorname {Sub}(\Gamma )\times \operatorname {Sub}(\Gamma ))$
which is invariant under
$\zeta \in \operatorname {Prob}(\operatorname {Sub}(\Gamma )\times \operatorname {Sub}(\Gamma ))$
which is invariant under
![]() $\Gamma \curvearrowright \operatorname {Sub}(\Gamma )\times \operatorname {Sub}(\Gamma )$
given by
$\Gamma \curvearrowright \operatorname {Sub}(\Gamma )\times \operatorname {Sub}(\Gamma )$
given by
![]() $g\cdot (K,H)=(gKg^{-1},gHg^{-1})$
and which satisfies
$g\cdot (K,H)=(gKg^{-1},gHg^{-1})$
and which satisfies
We will often use the language of probability and think of the
![]() $\operatorname {Sub}(\Gamma )$
-valued random variables
$\operatorname {Sub}(\Gamma )$
-valued random variables
![]() $K,H$
with distribution
$K,H$
with distribution
![]() $\eta _{1},\eta _{2}$
as the coupled invariant random subgroups. Thus, we will often say ‘let
$\eta _{1},\eta _{2}$
as the coupled invariant random subgroups. Thus, we will often say ‘let
![]() $K\leq H$
be a monotone joining of invariant random subgroups
$K\leq H$
be a monotone joining of invariant random subgroups
![]() $H,K$
’.
$H,K$
’.
In our context, given
![]() ${\mathcal S}\leq {\mathcal R}$
and
${\mathcal S}\leq {\mathcal R}$
and
![]() $\Gamma \leq N_{{\mathcal R}}({\mathcal S})$
we get a monotone joining of invariant random subgroups by considering the pushforward of
$\Gamma \leq N_{{\mathcal R}}({\mathcal S})$
we get a monotone joining of invariant random subgroups by considering the pushforward of
![]() $\mu $
under the map
$\mu $
under the map
![]() $\Gamma \to \operatorname {Sub}(\Gamma )\times \operatorname {Sub}(\Gamma )$
given by
$\Gamma \to \operatorname {Sub}(\Gamma )\times \operatorname {Sub}(\Gamma )$
given by
![]() $x\mapsto (\operatorname {Stab}_{\Gamma }(x),H_{x})$
. We can also reverse this construction.
$x\mapsto (\operatorname {Stab}_{\Gamma }(x),H_{x})$
. We can also reverse this construction.
Theorem 4.4. (Theorem 8.15 of [Reference Tucker-Drob38])
Let
![]() $\zeta \in \operatorname {Prob}(\operatorname {Sub}(\Gamma )\times \operatorname {Sub}(\Gamma ))$
be a monotone joining of invariant random subgroups
$\zeta \in \operatorname {Prob}(\operatorname {Sub}(\Gamma )\times \operatorname {Sub}(\Gamma ))$
be a monotone joining of invariant random subgroups
![]() $\eta _{1},\eta _{2}$
. Then there is a standard probability space
$\eta _{1},\eta _{2}$
. Then there is a standard probability space
![]() $(X,\mu )$
, a probability-measure-preserving action
$(X,\mu )$
, a probability-measure-preserving action
![]() $\Gamma \curvearrowright (X,\mu )$
and a normal subrelation
$\Gamma \curvearrowright (X,\mu )$
and a normal subrelation
![]() ${\mathcal S}$
of the orbit equivalence relation of
${\mathcal S}$
of the orbit equivalence relation of
![]() $\Gamma \curvearrowright (X,\mu )$
with the following property. We have that
$\Gamma \curvearrowright (X,\mu )$
with the following property. We have that
![]() $\Gamma \leq N_{{\mathcal R}}({\mathcal S})$
, and if we set
$\Gamma \leq N_{{\mathcal R}}({\mathcal S})$
, and if we set
and define
![]() $\Theta \colon X\to \operatorname {Sub}(\Gamma )\times \operatorname {Sub}(\Gamma )$
by
$\Theta \colon X\to \operatorname {Sub}(\Gamma )\times \operatorname {Sub}(\Gamma )$
by
![]() $\Theta (x)=(\operatorname {Stab}_{\Gamma }(x),H_{x})$
, then
$\Theta (x)=(\operatorname {Stab}_{\Gamma }(x),H_{x})$
, then
![]() $\zeta =(\Theta )_{*}(\mu )$
.
$\zeta =(\Theta )_{*}(\mu )$
.
So by Proposition 4.2 our question on co-spectral radii leads to another. Suppose that
![]() $K\leq H$
is a monotone joining of invariant random subgroups. Under what conditions do we have that
$K\leq H$
is a monotone joining of invariant random subgroups. Under what conditions do we have that
![]() $\rho (\Gamma /H,\nu )=\rho (\Gamma /K,\nu )$
almost surely? Let us first show that this is always true when K is co-amenable in H.
$\rho (\Gamma /H,\nu )=\rho (\Gamma /K,\nu )$
almost surely? Let us first show that this is always true when K is co-amenable in H.
Proposition 4.5. Suppose that
![]() $K\leq H\leq \Gamma $
are countable, discrete groups and that
$K\leq H\leq \Gamma $
are countable, discrete groups and that
![]() ${\nu \in \operatorname {Prob}(\Gamma )}$
. If K is co-amenable in
${\nu \in \operatorname {Prob}(\Gamma )}$
. If K is co-amenable in
![]() $H,$
then
$H,$
then
![]() $\rho (\Gamma /H,\nu )=\rho (\Gamma /K,\nu )$
.
$\rho (\Gamma /H,\nu )=\rho (\Gamma /K,\nu )$
.
Proof. To say that K is co-amenable in H means that the trivial representation of H is weakly contained in the quasi-regular representation of H on
![]() $\ell ^{2}(H/K)$
. By induction of representations, it follows that the quasi-regular representation of
$\ell ^{2}(H/K)$
. By induction of representations, it follows that the quasi-regular representation of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\ell ^{2}(\Gamma /H)$
is weakly contained in the quasi-regular representation of
$\ell ^{2}(\Gamma /H)$
is weakly contained in the quasi-regular representation of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\ell ^{2}(\Gamma /K)$
[Reference Bekka, de la Harpe and Valette8, Example E.1.8(ii), Theorem F.3.5]. This implies [Reference Bekka, de la Harpe and Valette8, Theorem F.4.4] that
$\ell ^{2}(\Gamma /K)$
[Reference Bekka, de la Harpe and Valette8, Example E.1.8(ii), Theorem F.3.5]. This implies [Reference Bekka, de la Harpe and Valette8, Theorem F.4.4] that
where
![]() $\unicode{x3bb} _{H}\colon \Gamma \to \mathcal {U}(\ell ^{2}(\Gamma /H))$
,
$\unicode{x3bb} _{H}\colon \Gamma \to \mathcal {U}(\ell ^{2}(\Gamma /H))$
,
![]() $\unicode{x3bb} _{K}\colon \Gamma \to \mathcal {U}(\ell ^{2}(\Gamma /H))$
are the quasi-regular representations. The reverse inequality is direct to argue, so this completes the proof.
$\unicode{x3bb} _{K}\colon \Gamma \to \mathcal {U}(\ell ^{2}(\Gamma /H))$
are the quasi-regular representations. The reverse inequality is direct to argue, so this completes the proof.
Notice that if
![]() $\Gamma ,H_{x},\operatorname {Stab}(x)$
are as in Theorem 4.4, then having
$\Gamma ,H_{x},\operatorname {Stab}(x)$
are as in Theorem 4.4, then having
![]() $\operatorname {Stab}(x)$
be co-amenable in
$\operatorname {Stab}(x)$
be co-amenable in
![]() $H_{x}$
does not guarantee that
$H_{x}$
does not guarantee that
![]() ${\mathcal S}$
is hyperfinite. So from Theorem 4.4 and Proposition 4.5 we get an example of an equivalent relation
${\mathcal S}$
is hyperfinite. So from Theorem 4.4 and Proposition 4.5 we get an example of an equivalent relation
![]() ${\mathcal R}$
, a
${\mathcal R}$
, a
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
and a normal
$\nu \in \operatorname {Prob}([{\mathcal R}])$
and a normal
![]() ${\mathcal S}\triangleleft {\mathcal R}$
, so that
${\mathcal S}\triangleleft {\mathcal R}$
, so that
![]() ${\mathcal S}$
is not hyperfinite, and yet
${\mathcal S}$
is not hyperfinite, and yet
![]() $\rho ({\mathcal R},\nu )=\rho ({\mathcal R}/{\mathcal S},\nu )$
. So a naive generalization of Kesten’s theorem does not hold in this context. In fact, there is even a monotone joining of invariant random subgroups
$\rho ({\mathcal R},\nu )=\rho ({\mathcal R}/{\mathcal S},\nu )$
. So a naive generalization of Kesten’s theorem does not hold in this context. In fact, there is even a monotone joining of invariant random subgroups
![]() $K\leq H$
of
$K\leq H$
of
![]() $\Gamma $
so that
$\Gamma $
so that
![]() $K\leq H$
is almost surely not co-amenable, and yet still
$K\leq H$
is almost surely not co-amenable, and yet still
![]() $\rho (\Gamma /K,\nu )=\rho (\Gamma /H,\nu )<1$
for every finitely supported
$\rho (\Gamma /K,\nu )=\rho (\Gamma /H,\nu )<1$
for every finitely supported
![]() $\nu \in \operatorname {Prob}(\Gamma )$
whose support generates
$\nu \in \operatorname {Prob}(\Gamma )$
whose support generates
![]() $\Gamma $
.
$\Gamma $
.
Example 4.6. (Counterexample to the converse of Proposition 4.5.) Let G be a non-amenable finitely generated group and let
![]() $\Gamma ={\mathbb F}_{2}\wr G$
be the wreath product of
$\Gamma ={\mathbb F}_{2}\wr G$
be the wreath product of
![]() ${\mathbb F}_{2}$
with G. Let
${\mathbb F}_{2}$
with G. Let
![]() $N:=\bigoplus _{{\mathbb F}_2}G$
. Recall that
$N:=\bigoplus _{{\mathbb F}_2}G$
. Recall that
![]() $\Gamma ={\mathbb F}_2\rtimes N$
with
$\Gamma ={\mathbb F}_2\rtimes N$
with
![]() $\gamma \in {\mathbb F}_2$
acting on N by
$\gamma \in {\mathbb F}_2$
acting on N by
![]() $\gamma ((g_\unicode{x3bb} )_\unicode{x3bb} )\gamma ^{-1}=(g_\unicode{x3bb} )_{\gamma \unicode{x3bb} }$
. For any subset
$\gamma ((g_\unicode{x3bb} )_\unicode{x3bb} )\gamma ^{-1}=(g_\unicode{x3bb} )_{\gamma \unicode{x3bb} }$
. For any subset
![]() $\Sigma \subset {\mathbb F}_2$
let
$\Sigma \subset {\mathbb F}_2$
let
![]() $N_\Sigma $
be the subgroup
$N_\Sigma $
be the subgroup
![]() $\bigoplus _{\unicode{x3bb} \in \Sigma }G.$
By construction,
$\bigoplus _{\unicode{x3bb} \in \Sigma }G.$
By construction,
![]() $N_\Sigma $
is a normal subgroup of N, and for every
$N_\Sigma $
is a normal subgroup of N, and for every
![]() $\gamma \in {\mathbb F}_2$
we have
$\gamma \in {\mathbb F}_2$
we have
![]() $\gamma N_\Sigma \gamma ^{-1}=N_{\gamma \Sigma }$
. This defines a
$\gamma N_\Sigma \gamma ^{-1}=N_{\gamma \Sigma }$
. This defines a
![]() $\Gamma $
-equivariant map
$\Gamma $
-equivariant map
A percolation on
![]() ${\mathbb F}_2$
is random subset of
${\mathbb F}_2$
is random subset of
![]() ${\mathbb F}_2$
with distribution invariant under left translations. For any percolation
${\mathbb F}_2$
with distribution invariant under left translations. For any percolation
![]() $P\in \{0,1\}^{{\mathbb F}_2}$
the group
$P\in \{0,1\}^{{\mathbb F}_2}$
the group
![]() $N_P$
is an invariant random subgroup of
$N_P$
is an invariant random subgroup of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $p<q\in (0,1)$
and let
$p<q\in (0,1)$
and let
![]() $(P,Q)\in \{0,1\}^{{\mathbb F}_2}\times \{0,1\}^{{\mathbb F}_2}$
be a
$(P,Q)\in \{0,1\}^{{\mathbb F}_2}\times \{0,1\}^{{\mathbb F}_2}$
be a
![]() $\Gamma $
-invariant coupling of two Bernoulli percolations of parameters p and q respectively such that
$\Gamma $
-invariant coupling of two Bernoulli percolations of parameters p and q respectively such that
![]() $P\subset Q$
almost surely. This can be arranged by first choosing P as a Bernoulli percolation of parameter p and then declaring Q to be the union of P and an independent copy of a Bernoulli percolation with parameter
$P\subset Q$
almost surely. This can be arranged by first choosing P as a Bernoulli percolation of parameter p and then declaring Q to be the union of P and an independent copy of a Bernoulli percolation with parameter
![]() $({q-p})/({1-p})$
. In this way we construct an invariant random couple of subgroups
$({q-p})/({1-p})$
. In this way we construct an invariant random couple of subgroups
![]() $N_{P}\subset N_{Q}$
.
$N_{P}\subset N_{Q}$
.
The set
![]() $Q\setminus P$
is infinite almost surely, so the quotient
$Q\setminus P$
is infinite almost surely, so the quotient
![]() $N_Q/N_P$
is the direct sum of infinitely many copies of G. In particular,
$N_Q/N_P$
is the direct sum of infinitely many copies of G. In particular,
![]() $N_P$
is almost surely not co-amenable in
$N_P$
is almost surely not co-amenable in
![]() $N_Q$
. Let S be a finite generating set for
$N_Q$
. Let S be a finite generating set for
![]() $\Gamma $
. We claim that
$\Gamma $
. We claim that
This will follow quite quickly from the semicontinuity properties of the co-spectral radius. Since P is a Bernoulli percolation, for any
![]() $n\in \mathbb N$
we will almost surely find
$n\in \mathbb N$
we will almost surely find
![]() $\gamma _n\in {\mathbb F}_2$
such that
$\gamma _n\in {\mathbb F}_2$
such that
![]() $\gamma P$
contains the R-ball around the identity. The sequence of subgroups
$\gamma P$
contains the R-ball around the identity. The sequence of subgroups
![]() $N_{\gamma _nP}$
converges to N in
$N_{\gamma _nP}$
converges to N in
![]() $\operatorname {Sub}(\Gamma )$
. On the other hand
$\operatorname {Sub}(\Gamma )$
. On the other hand
![]() $\rho (\Gamma /N_{\gamma _nP},S)=\rho (\Gamma /N_{P},S)$
, because
$\rho (\Gamma /N_{\gamma _nP},S)=\rho (\Gamma /N_{P},S)$
, because
![]() $N_{\gamma _nP}=\gamma _n N_P\gamma _n^{-1}.$
By Lemma 4.7 we conclude that
$N_{\gamma _nP}=\gamma _n N_P\gamma _n^{-1}.$
By Lemma 4.7 we conclude that
![]() $\rho (\Gamma /N_P,S)\geq \rho (\Gamma /N,S)$
. The reverse inequality is clear, so
$\rho (\Gamma /N_P,S)\geq \rho (\Gamma /N,S)$
. The reverse inequality is clear, so
![]() $\rho (\Gamma /N_P,S)=\rho (\Gamma /N,S).$
In the same way we show that
$\rho (\Gamma /N_P,S)=\rho (\Gamma /N,S).$
In the same way we show that
![]() $\rho (\Gamma /N_Q,S)=\rho (\Gamma /N,S).$
$\rho (\Gamma /N_Q,S)=\rho (\Gamma /N,S).$
Lemma 4.7. Let
![]() $\Gamma $
be a countable group generated by a finite symmetric set S. Let
$\Gamma $
be a countable group generated by a finite symmetric set S. Let
![]() $\Lambda _n$
be a sequence of subgroups of
$\Lambda _n$
be a sequence of subgroups of
![]() $\Gamma $
converging to a subgroup
$\Gamma $
converging to a subgroup
![]() $\Lambda _\infty \subset \Gamma $
in
$\Lambda _\infty \subset \Gamma $
in
![]() $\operatorname {Sub}(\Gamma )$
. We have
$\operatorname {Sub}(\Gamma )$
. We have
Proof. For any subgroup
![]() $\Lambda \subset \Gamma $
let
$\Lambda \subset \Gamma $
let
![]() $B_\Lambda (R)$
denote the R-ball around the trivial coset in the Schreier graph
$B_\Lambda (R)$
denote the R-ball around the trivial coset in the Schreier graph
![]() $\mathrm {Sch}(\Gamma /\Lambda , S).$
We will write P for the Markov transition operator
$\mathrm {Sch}(\Gamma /\Lambda , S).$
We will write P for the Markov transition operator
![]() $P=({1}/{|S|})\sum _{s\in S} s.$
Let
$P=({1}/{|S|})\sum _{s\in S} s.$
Let
![]() $\varepsilon>0$
and let
$\varepsilon>0$
and let
![]() $f\in \ell ^2(\Gamma /\Lambda _\infty )$
be a non-zero finitely supported function such that
$f\in \ell ^2(\Gamma /\Lambda _\infty )$
be a non-zero finitely supported function such that
Choose
![]() $R>0$
such that the support of f is contained in
$R>0$
such that the support of f is contained in
![]() $B_{\Lambda _\infty }(R)$
. For big enough n we will have an isomorphism between labeled graphs
$B_{\Lambda _\infty }(R)$
. For big enough n we will have an isomorphism between labeled graphs
![]() $\iota _n\colon B_{\Lambda _n}(R+1)\simeq B_{\Lambda _\infty }(R+1).$
Let
$\iota _n\colon B_{\Lambda _n}(R+1)\simeq B_{\Lambda _\infty }(R+1).$
Let
![]() $f_n=f\circ \iota _n$
be the pullback of f to
$f_n=f\circ \iota _n$
be the pullback of f to
![]() $\ell ^2(\Gamma /\Lambda _n)$
. Then
$\ell ^2(\Gamma /\Lambda _n)$
. Then
We deduce that
![]() $\liminf _{n\to \infty }\rho (\Gamma /\Lambda _n,S)\geq \rho (\Gamma /\Lambda _\infty ,S)-\varepsilon $
. We finish the proof by taking
$\liminf _{n\to \infty }\rho (\Gamma /\Lambda _n,S)\geq \rho (\Gamma /\Lambda _\infty ,S)-\varepsilon $
. We finish the proof by taking
![]() $\varepsilon \to 0$
.
$\varepsilon \to 0$
.
5. Co-spectral radius and percolation
Let
![]() $(G,o)$
be a transitive graph with the root at o (respectively, unimodular random graph). A invariant percolation P is a random subset of edges of G, such that the distribution of P is invariant under graph automorphisms (respectively, invariant under the rerooting equivalence relation).
$(G,o)$
be a transitive graph with the root at o (respectively, unimodular random graph). A invariant percolation P is a random subset of edges of G, such that the distribution of P is invariant under graph automorphisms (respectively, invariant under the rerooting equivalence relation).
Theorem 5.1. Let P be an invariant bond percolation on a unimodular random graph
![]() $(\mathcal G,o)$
of degree at most d. Let C be the connected component of o in the percolation P. Let
$(\mathcal G,o)$
of degree at most d. Let C be the connected component of o in the percolation P. Let
![]() $X_n$
be the standard random walk on
$X_n$
be the standard random walk on
![]() $\mathcal G$
starting at o. The limit
$\mathcal G$
starting at o. The limit
exists almost surely.
Proof. The fist step is to use Proposition 2.1 to construct an associated probability-measure-preserving equivalence relation with a graphing and a subrelation that will allow us to apply Theorem 1.2. We now borrow the notation from §3 and Proposition 2.1. Let
![]() $(G,o),P$
be an instance of the percolation and let
$(G,o),P$
be an instance of the percolation and let
![]() $x=((G,o),P,\unicode{x3bb} )\in \Omega _\#$
with an i.i.d. random coloring
$x=((G,o),P,\unicode{x3bb} )\in \Omega _\#$
with an i.i.d. random coloring
![]() $\unicode{x3bb} $
. The graph
$\unicode{x3bb} $
. The graph
![]() $(\mathcal G_x,x)$
is isomorphic to
$(\mathcal G_x,x)$
is isomorphic to
![]() $(G,o)$
almost surely. Since
$(G,o)$
almost surely. Since
![]() $C=[x]_{\mathcal S}$
almost surely, the probability of returning to the connected component of P containing the root o at time n is the same as
$C=[x]_{\mathcal S}$
almost surely, the probability of returning to the connected component of P containing the root o at time n is the same as
![]() $p_{n,x,{\mathcal S}}^{\nu }$
. We have
$p_{n,x,{\mathcal S}}^{\nu }$
. We have
The limit on the right-hand side exists for
![]() $\mu _\#$
almost all x, by virtue of Theorem 1.2.
$\mu _\#$
almost all x, by virtue of Theorem 1.2.
5.1. Critical values from spectral radius
Using Theorem 5.1, we can define two new critical values of the Bernoulli bond percolation that fit nicely with the existing classical exponents like
![]() $p_c,p_u,p_{[2\to 2]}$
and
$p_c,p_u,p_{[2\to 2]}$
and
![]() $p_{\mathrm {exp}}$
. We recall their definitions below.
$p_{\mathrm {exp}}$
. We recall their definitions below.
![]() ${\mathcal B}_p$
denotes the Bernoulli bond percolation with parameter
${\mathcal B}_p$
denotes the Bernoulli bond percolation with parameter
![]() $p\in [0,1]$
. For simplicity we restrict to transitive rooted graph
$p\in [0,1]$
. For simplicity we restrict to transitive rooted graph
![]() $(G,o)$
, but the definitions below can be easily adapted to all ergodic unimodular random graphs.
$(G,o)$
, but the definitions below can be easily adapted to all ergodic unimodular random graphs.
-
•
 $p_u$
is defined as the infimum of
$p_u$
is defined as the infimum of
 $p\in [0,1]$
such that
$p\in [0,1]$
such that
 ${\mathcal B}_p$
has a unique infinite connected component almost surely.
${\mathcal B}_p$
has a unique infinite connected component almost surely. -
•
 $p_c$
is defined as the infimum of
$p_c$
is defined as the infimum of
 $p\in [0,1]$
such that
$p\in [0,1]$
such that
 ${\mathcal B}_p$
has an infinite connected component almost surely.
${\mathcal B}_p$
has an infinite connected component almost surely. -
• For
 $x,y\in V(G)$
let
$x,y\in V(G)$
let
 $\tau _p(x,y)$
denote the probability that x and y are connected in
$\tau _p(x,y)$
denote the probability that x and y are connected in
 ${\mathcal B}_p$
. The exponent
${\mathcal B}_p$
. The exponent
 $p_{\mathrm {exp}}$
is the supremum of all p such that
$p_{\mathrm {exp}}$
is the supremum of all p such that
 $\tau _p(x,y)$
decays exponentially in
$\tau _p(x,y)$
decays exponentially in
 $\operatorname {d}(x,y)$
.
$\operatorname {d}(x,y)$
. -
• Consider the operator
 $T_p$
acting on compactly functions on
$T_p$
acting on compactly functions on
 $V(G)$
defined by The exponent
$V(G)$
defined by The exponent $$ \begin{align*}T_p(\phi)(x)=\sum_{y\in V(G)}\tau_p(x,y)\phi(y).\end{align*} $$
$$ \begin{align*}T_p(\phi)(x)=\sum_{y\in V(G)}\tau_p(x,y)\phi(y).\end{align*} $$
 $p_{[2\to 2]}$
is the supremum of p such that
$p_{[2\to 2]}$
is the supremum of p such that
 $T_p$
defines a bounded operator
$T_p$
defines a bounded operator
 $\ell ^2(V(G))\to \ell ^2(V(G))$
[Reference Hutchcroft21, §2].
$\ell ^2(V(G))\to \ell ^2(V(G))$
[Reference Hutchcroft21, §2].
For quasi-transitive graphs, these numbers satisfy the inequalities
![]() $p_c\leq p_{[2\to 2]}\leq p_{\mathrm {exp}}\leq p_u$
, ([Reference Aizenman and Barsky5], [Reference Duminil-Copin and Tassion13, Theorem 1.1.2], [Reference Hutchcroft23, Theorem 2.2]). We add two more specimens to this zoo of critical values. They implicitly depend on the random walk; we always choose the standard one.
$p_c\leq p_{[2\to 2]}\leq p_{\mathrm {exp}}\leq p_u$
, ([Reference Aizenman and Barsky5], [Reference Duminil-Copin and Tassion13, Theorem 1.1.2], [Reference Hutchcroft23, Theorem 2.2]). We add two more specimens to this zoo of critical values. They implicitly depend on the random walk; we always choose the standard one.
Definition 5.2
-
(1) Let
 $p_{\mathrm {Ram}}$
(for Ramanujan) be the supremum of p such that
$p_{\mathrm {Ram}}$
(for Ramanujan) be the supremum of p such that
 ${\rho _{{\mathcal B}_p}=\rho _{G}.}$
${\rho _{{\mathcal B}_p}=\rho _{G}.}$
-
(2) Let
 $p_{\mathrm {cK}}$
(for co-Kaimanovich) be the infimum of p such that
$p_{\mathrm {cK}}$
(for co-Kaimanovich) be the infimum of p such that
 $\rho _{{\mathcal B}_p}=1.$
$\rho _{{\mathcal B}_p}=1.$
The reason for the term ‘co-Kaimanovich’ is as follows. For the spectral radius (as opposed to the co-spectral radius) of relations
![]() ${\mathcal R}$
, having
${\mathcal R}$
, having
![]() $\rho ({\mathcal R},\nu )=1$
for some countably supported
$\rho ({\mathcal R},\nu )=1$
for some countably supported
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
whose support generates
$\nu \in \operatorname {Prob}([{\mathcal R}])$
whose support generates
![]() ${\mathcal R}$
is not equivalent to hyperfiniteness of
${\mathcal R}$
is not equivalent to hyperfiniteness of
![]() ${\mathcal R}$
, as discussed in detail in work of Kaimanovich [Reference Kaimanovich27]. This work of Kaimanovich greatly clarified a common misconception in the literature, and gave precise and tractable criteria to verify when a relation is hyperfinite in terms of the data of several spectral radii. For example, this work shows that spectral radius
${\mathcal R}$
, as discussed in detail in work of Kaimanovich [Reference Kaimanovich27]. This work of Kaimanovich greatly clarified a common misconception in the literature, and gave precise and tractable criteria to verify when a relation is hyperfinite in terms of the data of several spectral radii. For example, this work shows that spectral radius
![]() $1$
is equivalent to having
$1$
is equivalent to having
![]() $\rho ({\mathcal R},\nu )=1$
for every countably supported
$\rho ({\mathcal R},\nu )=1$
for every countably supported
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
whose support generates
$\nu \in \operatorname {Prob}([{\mathcal R}])$
whose support generates
![]() ${\mathcal R}$
. It is thus reasonable to call a relation
${\mathcal R}$
. It is thus reasonable to call a relation
![]() ${\mathcal R}$
Kaimanovich if there is a
${\mathcal R}$
Kaimanovich if there is a
![]() $\nu \in \operatorname {Prob}([{\mathcal R}])$
whose support generates
$\nu \in \operatorname {Prob}([{\mathcal R}])$
whose support generates
![]() ${\mathcal R}$
and has
${\mathcal R}$
and has
![]() $\rho ({\mathcal R},\nu )=1$
. Since the co-spectral radius heuristically plays the role of the spectral radius in a quotient, this motivates the term ‘co-Kaimanovich’.
$\rho ({\mathcal R},\nu )=1$
. Since the co-spectral radius heuristically plays the role of the spectral radius in a quotient, this motivates the term ‘co-Kaimanovich’.
We now compare how these critical values are related.
Proposition 5.3
-
(1)
 $p_{\mathrm {Ram}}\leq p_{\mathrm {cK}}$
.
$p_{\mathrm {Ram}}\leq p_{\mathrm {cK}}$
. -
(2)
 $p_{\mathrm {cK}}\leq p_u$
.
$p_{\mathrm {cK}}\leq p_u$
. -
(3)
 $p_{\mathrm {exp}}\leq p_{\mathrm {cK}}$
.
$p_{\mathrm {exp}}\leq p_{\mathrm {cK}}$
. -
(4)
 $p_{[2\to 2]}\leq p_{\mathrm {Ram}}$
.
$p_{[2\to 2]}\leq p_{\mathrm {Ram}}$
.
We remark that (4) is equivalent to a theorem of Hutchcroft [Reference Hutchcroft21, Proposition 6.4], but as our proof is short we include the proof for completeness.
Proof. (1) If G is amenable, then
![]() $1\geq \rho _{{\mathcal B}_{p}}\geq \rho _{G}\geq 1$
. If G is non-amenable, then
$1\geq \rho _{{\mathcal B}_{p}}\geq \rho _{G}\geq 1$
. If G is non-amenable, then
![]() $\rho _{G}<1$
. The inequality follows now from the obvious monotonicity of
$\rho _{G}<1$
. The inequality follows now from the obvious monotonicity of
![]() $\rho _{{\mathcal B}_p}$
in p.
$\rho _{{\mathcal B}_p}$
in p.
(2) Let
![]() $p>p_{u}$
. Let
$p>p_{u}$
. Let
![]() ${\mathcal S}\leq {\mathcal R}$
be the inclusion of equivalence relations constructed in Proposition 2.1. The infinite connected component of
${\mathcal S}\leq {\mathcal R}$
be the inclusion of equivalence relations constructed in Proposition 2.1. The infinite connected component of
![]() ${\mathcal B}_{p}$
in the percolated graph corresponds to an
${\mathcal B}_{p}$
in the percolated graph corresponds to an
![]() ${\mathcal S}$
-invariant positive measure subset
${\mathcal S}$
-invariant positive measure subset
![]() $E\subseteq \Omega _\#$
(namely,
$E\subseteq \Omega _\#$
(namely,
![]() $E=\{\omega :[\omega ]_{{\mathcal S}} \text {is infinite}\}$
). Uniqueness of the infinite connected component tells us that
$E=\{\omega :[\omega ]_{{\mathcal S}} \text {is infinite}\}$
). Uniqueness of the infinite connected component tells us that
![]() ${\mathcal R}|_{E}={\mathcal S}|_{E}$
. For
${\mathcal R}|_{E}={\mathcal S}|_{E}$
. For
![]() $l\in {\mathbb N}$
, we let
$l\in {\mathbb N}$
, we let
![]() $p_{l,x,E}$
be the probability that the random walk starting at x is in E after l steps. Since
$p_{l,x,E}$
be the probability that the random walk starting at x is in E after l steps. Since
![]() ${\mathcal R}|_{E}={\mathcal S}|_{E}$
, we have
${\mathcal R}|_{E}={\mathcal S}|_{E}$
, we have
![]() $p_{2n,x,{\mathcal S}}\geq p_{2n,x,E}$
. Thus, for almost every
$p_{2n,x,{\mathcal S}}\geq p_{2n,x,E}$
. Thus, for almost every
![]() $x\in X$
we have
$x\in X$
we have
where in the first equality we use Theorem 3.20. Since
![]() $\mu (E)>0$
we obtain that
$\mu (E)>0$
we obtain that
(3) Let
Then
![]() $p_{\mathrm {exp}}=\sup \{p\in [0,1] | \xi _p>0\}.$
Let
$p_{\mathrm {exp}}=\sup \{p\in [0,1] | \xi _p>0\}.$
Let
![]() $p<p_{\mathrm {exp}}$
. The spheres in G grow at most exponentially fast, so there exists
$p<p_{\mathrm {exp}}$
. The spheres in G grow at most exponentially fast, so there exists
![]() $q>1$
such that
$q>1$
such that
We have
By the Hölder inequality,
By the Riesz–Thorin theorem
Hence,
![]() $p_n(o,[o]_{{\mathcal B}_p})\leq A \rho _G^{{2n}/{q}}$
. The upper bound decays exponentially in n, so
$p_n(o,[o]_{{\mathcal B}_p})\leq A \rho _G^{{2n}/{q}}$
. The upper bound decays exponentially in n, so
![]() $\rho _{{\mathcal B}_p}<1.$
This proves that
$\rho _{{\mathcal B}_p}<1.$
This proves that
![]() $p_{\mathrm {exp}}\leq p_{\mathrm {cK}}.$
$p_{\mathrm {exp}}\leq p_{\mathrm {cK}}.$
(4) Let
![]() $p<p_{[2\to 2]}$
, so that
$p<p_{[2\to 2]}$
, so that
![]() $\|T_p\|_{L^2\to L^2}<\infty $
. Fix the root
$\|T_p\|_{L^2\to L^2}<\infty $
. Fix the root
![]() $o\in V(G)$
and let
$o\in V(G)$
and let
![]() $v\in V(G)$
be a vertex. Let
$v\in V(G)$
be a vertex. Let
![]() $f_n(v):=p_n(o,v)$
, that is, the probability of going from o to v in time n. Note that
$f_n(v):=p_n(o,v)$
, that is, the probability of going from o to v in time n. Note that
![]() $\|f_n\|_2^2=p_{2n}(o,o).$
We have
$\|f_n\|_2^2=p_{2n}(o,o).$
We have
The operator
![]() $T_p$
is bounded, so
$T_p$
is bounded, so
![]() $\|T_p f_n\|_2\ll \|f_n\|_2$
. We deduce that
$\|T_p f_n\|_2\ll \|f_n\|_2$
. We deduce that
The reverse inequality
![]() $\rho _G\leq \rho _{{\mathcal B}_p}$
is always true so
$\rho _G\leq \rho _{{\mathcal B}_p}$
is always true so
![]() $\rho _{{\mathcal B}_p}=\rho _G$
. This demonstrates that
$\rho _{{\mathcal B}_p}=\rho _G$
. This demonstrates that
![]() ${p\leq p_{\mathrm {Ram}}}$
. It follows that
${p\leq p_{\mathrm {Ram}}}$
. It follows that
![]() $p_{[2\to 2]}\leq p_{\mathrm {Ram}}$
.
$p_{[2\to 2]}\leq p_{\mathrm {Ram}}$
.
Example 5.4. Let
![]() $\mathcal T_d$
be the d-regular tree. We have
$\mathcal T_d$
be the d-regular tree. We have
![]() $p_{\mathrm {cK}}=1$
and
$p_{\mathrm {cK}}=1$
and
![]() $p_{\mathrm {Ram}}=\tfrac 12.$
$p_{\mathrm {Ram}}=\tfrac 12.$
5.2. Walk growth
Let
![]() $(G,o)$
be a unimodular random graph with degree at most
$(G,o)$
be a unimodular random graph with degree at most
![]() $d\in {\mathbb N}$
. Let
$d\in {\mathbb N}$
. Let
![]() ${\mathcal M}_{d}$
be the space of rooted graphs where each vertex has degree at most d, modulo isomorphism. This can be turned into a compact metric space with the distance
${\mathcal M}_{d}$
be the space of rooted graphs where each vertex has degree at most d, modulo isomorphism. This can be turned into a compact metric space with the distance
Recall that the distribution
![]() $\eta $
of
$\eta $
of
![]() $[(G,o)]$
is a probability measure on
$[(G,o)]$
is a probability measure on
![]() ${\mathcal M}_{d}$
which is invariant under the rerooting equivalence relation
${\mathcal M}_{d}$
which is invariant under the rerooting equivalence relation
(we remark that
![]() $\eta $
being rerooting invariant does not characterize unimodularity, but that will not cause an issue for us here). Let
$\eta $
being rerooting invariant does not characterize unimodularity, but that will not cause an issue for us here). Let
![]() $w_{n}(o)$
be the number of walks of length n starting at o.
$w_{n}(o)$
be the number of walks of length n starting at o.
Note that, by Proposition 2.1, we can find a probability-measure-preserving countable equivalence relation
![]() $(\Omega _{\#},\nu _{\#},{\mathcal R})$
with a generating graph
$(\Omega _{\#},\nu _{\#},{\mathcal R})$
with a generating graph
![]() $\Phi =(\phi _{i})_{i\in I}$
so that the distribution of
$\Phi =(\phi _{i})_{i\in I}$
so that the distribution of
![]() $[({\mathcal G},o)]$
is the law of the rooted graph
$[({\mathcal G},o)]$
is the law of the rooted graph
![]() $({\mathcal G}_{\omega },\omega )$
defined for
$({\mathcal G}_{\omega },\omega )$
defined for
![]() $\omega \in \Omega _{\#}$
where the vertex set of
$\omega \in \Omega _{\#}$
where the vertex set of
![]() ${\mathcal G}_{\omega }$
is
${\mathcal G}_{\omega }$
is
![]() $[\omega ]_{{\mathcal R}}$
and the edge set
$[\omega ]_{{\mathcal R}}$
and the edge set
![]() $\{(\omega ',\phi _{i}^{\pm 1}(\omega '):w'\in [\omega ]_{{\mathcal R}},i\in I\}$
. Define
$\{(\omega ',\phi _{i}^{\pm 1}(\omega '):w'\in [\omega ]_{{\mathcal R}},i\in I\}$
. Define
![]() $f_{k}\colon {\mathcal R}\to [0,+\infty )$
by declaring
$f_{k}\colon {\mathcal R}\to [0,+\infty )$
by declaring
![]() $f_{k}(x,y)$
to be the number of paths from x to y in
$f_{k}(x,y)$
to be the number of paths from x to y in
![]() $G_{x}$
. It is direct to verify the hypotheses of Theorem 3.7 and thus
$G_{x}$
. It is direct to verify the hypotheses of Theorem 3.7 and thus
 $$ \begin{align*}\lim_{k\to\infty}\bigg(\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg)^{1/k}\end{align*} $$
$$ \begin{align*}\lim_{k\to\infty}\bigg(\sum_{y\in [x]_{{\mathcal R}}}f_{k}(x,y)\bigg)^{1/k}\end{align*} $$
exists almost everywhere. The above sum has the same law as
![]() $w_{k}(o)$
, and this proves that
$w_{k}(o)$
, and this proves that
![]() $\lim _{n\to \infty }({1}/{n})\log w_{n}(o)$
exists.
$\lim _{n\to \infty }({1}/{n})\log w_{n}(o)$
exists.
Theorem 5.5. Fix notation as above, and suppose
![]() $\eta $
is ergodic under the rerooting equivalence relation. Define
$\eta $
is ergodic under the rerooting equivalence relation. Define
![]() $A\in B(L^{2}({\mathcal M}_{d},\eta ))$
by
$A\in B(L^{2}({\mathcal M}_{d},\eta ))$
by
Then
Proof. Observe that if
![]() $o'$
is a vertex in the rooted graph
$o'$
is a vertex in the rooted graph
![]() $(G,o)$
and if
$(G,o)$
and if
![]() $l=d_{G}(o,o')$
, then
$l=d_{G}(o,o')$
, then
and so
Thus, by ergodicity,
![]() $\lim _{n\to \infty }w_{n}(o)^{1/n}$
is almost surely constant. By Theorem 3.7(ii) this constant equals
$\lim _{n\to \infty }w_{n}(o)^{1/n}$
is almost surely constant. By Theorem 3.7(ii) this constant equals
A direct calculation shows that
![]() $\langle A^{k}1,1 \rangle ={\mathbb E}(w_{k}(o)).$
Note that
$\langle A^{k}1,1 \rangle ={\mathbb E}(w_{k}(o)).$
Note that
and that
![]() $\langle A^{k}1_{E},1_{E} \rangle \leq \langle A^{k}1,1 \rangle $
for all measurable sets E. Thus, the same argument as in Theorem 3.2(i) using Lemma 3.5 shows that (5.1) is equal to
$\langle A^{k}1_{E},1_{E} \rangle \leq \langle A^{k}1,1 \rangle $
for all measurable sets E. Thus, the same argument as in Theorem 3.2(i) using Lemma 3.5 shows that (5.1) is equal to
![]() $\|A\|$
.
$\|A\|$
.
Acknowledgements
Much of the work by the last named author was done on visits to the Rényi Institute in Budapest. He would like to thank the Rényi Institute for its hospitality. We would like to thank Gabor Pete for helpful conversations. We thank the anonymous referee for their numerous comments, which greatly improved the paper. M. Abert acknowledges support from the KKP 139502 project, the ERC Consolidator Grant 648017 and the Lendulet Groups and Graphs research group. B. Hayes gratefully acknowledges support from the NSF grants DMS-1600802, DMS-1827376, and DMS-2000105. M. Fraczyk was partly supported by the Dioscuri Programme initiated by the Max Planck Society, jointly managed with the National Science Centre (Poland), and mutually funded by the Polish Ministry of Science and Higher Education and the German Federal Ministry of Education and Research.