Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-16T16:18:34.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Convex structures revisited

Published online by Cambridge University Press:  09 January 2015

LIVIU PĂUNESCU
LIVIU PĂUNESCU*
Affiliation:
Institute of Mathematics ‘S. Stoilow’ of the Romanian Academy, 21 Calea Grivitei Street, 010702 Bucharest, Romania email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide a complete characterization of extreme points of the space of sofic representations. We also show that the restriction map 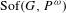$\text{Sof}(G,P^{{\it\omega}})$ to 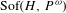$\text{Sof}(H,P^{{\it\omega}})$, where 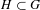$H\subset G$, is not always surjective. The first part of the paper is a continuation of Păunescu [A convex structure on sofic embeddings. Ergod. Th. & Dynam. Sys.34(4) (2014), 1343–1352] and follows more closely the plan of Brown [Topological dynamical systems associated to 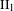$\text{II}_{1}$-factors. Adv. Math.227(4) (2011), 1665–1699].

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 5 , August 2016 , pp. 1596 - 1615
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abert, M., Glasner, Y. and Virag, B.. The measurable Kesten theorem. Preprint, 2012, arXiv:1111.2080.Google Scholar
Alon, N. and Milman, V. D.. 𝜆1 , isoperimetric inequalities for graphs and superconcentrators. J. Combin. Theory Ser. B 38 (1985), 73–88.Google Scholar
Brown, N.. Topological dynamical systems associated to II1 -factors. Adv. Math. 227(4) (2011), 1665–1699.Google Scholar
Capraro, V. and Fritz, T.. On the axiomatization of convex subsets of Banach spaces. Proc. Amer. Math. Soc. 141(6) (2013), 2127–2135.CrossRefGoogle Scholar
Connes, A., Feldman, J. and Weiss, B.. An amenable equivalence relation is generated by a single transformation. Ergod. Th. & Dynam. Sys. 1 (1981), 431–450.CrossRefGoogle Scholar
Elek, G. and Szabo, E.. Hyperlinearity, essentially free actions and L2-invariants. The sofic property. Math. Ann. 332(2) (2005), 421–441.CrossRefGoogle Scholar
Elek, G. and Szabo, E.. Sofic representations of amenable groups. Proc. Amer. Math. Soc. 139 (2011), 4285–4291.Google Scholar
Elek, G. and Szegedy, B.. Limits of hypergaphs, removal and regularity lemmas. A non-standard approach. Preprint, 2007, arXiv:0705.2179v1.Google Scholar
Friedman, J.. A Proof of Alon’s Second Eigenvalue Conjecture and Related Problems (Memoirs of the Americal Mathematical Society, 195) . American Mathematical Society, Providence, RI, 2008.Google Scholar
Jung, K.. Amenability, tubularity, and embeddings into R 𝜔 . Math. Ann. 338(1) (2007), 241–248.Google Scholar
Kerr, D. and Li, H.. Combinatorial independence and sofic entropy. Commun. Math. Stat. 1(2) (2013), 213–257.Google Scholar
Loeb, P. E.. Conversion from non-standard to standard measure spaces and applications in probability theory. Trans. Amer. Math. Soc. 211 (1975), 113–122.Google Scholar
Lubotzky, A.. Discrete Groups, Expanding Graphs and Invariant Measures (Progress in Mathematics, 125) . Birkhauser, Basel, 1994.Google Scholar
Moreno, R. and Rivera, L. M.. Blocks in cycles and $k$ -commuting permutations. Preprint, 2014, arXiv:1306.5708.Google Scholar
Păunescu, L.. On sofic actions and equivalence relations. J. Funct. Anal. 261(9) (2011), 2461–2485.CrossRefGoogle Scholar
Păunescu, L.. A convex structure on sofic embeddings. Ergod. Th. & Dynam. Sys. 34(4) (2014), 1343–1352.Google Scholar
Pestov, V. and Kwiatkowska, A.. An introduction to hyperlinear and sofic groups. Preprint, 2009, arXiv:0911.4266.Google Scholar