Article contents
 -Convergence to equilibrium and space—time bernoullicity for spin systems in the M < ε case
-Convergence to equilibrium and space—time bernoullicity for spin systems in the M < ε case
Published online by Cambridge University Press: 19 September 2008
Abstract
Liggett has proved that for spin systems, Markov processes with state space {0,1}ℤn, there is a unique stationary distribution in the M < ε regime and all initial configurations uniformly approach this unique stationary distribution exponentially in the weak topology. Here, M and ε are two parameters of the system. We extend this result to discrete time but strengthen it by proving exponential convergence in the stronger 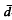 - metric instead of the usual weak topology. This is then used to show that the unique stationary process with state space {0,1}ℤn and index set ℤ is isomorphic (in the sense of ergodic theory) to an independent process indexed by ℤ. In the translation invariant case, we prove the stronger fact that this stationary process viewed as a {0, l}-valued process with index set ℤn × ℤ (spacetime) is isomorphic to an independent process also indexed by ℤn × ℤ. This shows that this process is in some sense the most random possible. An application of this last result to approximating by an infinite number of finite systems concatenated independently together is also presented. Finally, we extend all of these results to continuous time.
- metric instead of the usual weak topology. This is then used to show that the unique stationary process with state space {0,1}ℤn and index set ℤ is isomorphic (in the sense of ergodic theory) to an independent process indexed by ℤ. In the translation invariant case, we prove the stronger fact that this stationary process viewed as a {0, l}-valued process with index set ℤn × ℤ (spacetime) is isomorphic to an independent process also indexed by ℤn × ℤ. This shows that this process is in some sense the most random possible. An application of this last result to approximating by an infinite number of finite systems concatenated independently together is also presented. Finally, we extend all of these results to continuous time.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1991
References
REFERENCES
- 5
- Cited by


