Published online by Cambridge University Press: 04 December 2018
In this paper we consider 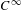 $C^{\infty }$-generic families of area-preserving diffeomorphisms of the torus homotopic to the identity and their rotation sets. Let
$C^{\infty }$-generic families of area-preserving diffeomorphisms of the torus homotopic to the identity and their rotation sets. Let 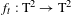 $f_{t}:\text{T}^{2}\rightarrow \text{T}^{2}$ be such a family,
$f_{t}:\text{T}^{2}\rightarrow \text{T}^{2}$ be such a family, 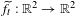 $\widetilde{f}_{t}:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$ be a fixed family of lifts and
$\widetilde{f}_{t}:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$ be a fixed family of lifts and 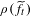 $\unicode[STIX]{x1D70C}(\widetilde{f}_{t})$ be their rotation sets, which we assume to have interior for
$\unicode[STIX]{x1D70C}(\widetilde{f}_{t})$ be their rotation sets, which we assume to have interior for  $t$ in a certain open interval
$t$ in a certain open interval  $I$. We also assume that some rational point
$I$. We also assume that some rational point 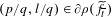 $(p/q,l/q)\in \unicode[STIX]{x2202}\unicode[STIX]{x1D70C}(\widetilde{f}_{\overline{t}})$ for a certain parameter
$(p/q,l/q)\in \unicode[STIX]{x2202}\unicode[STIX]{x1D70C}(\widetilde{f}_{\overline{t}})$ for a certain parameter 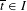 $\overline{t}\in I$, and we want to understand the consequences of the following hypothesis: for all
$\overline{t}\in I$, and we want to understand the consequences of the following hypothesis: for all 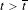 $t>\overline{t}$,
$t>\overline{t}$, 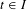 $t\in I$,
$t\in I$,  $(p/q,l/q)\in \text{int}(\unicode[STIX]{x1D70C}(\widetilde{f}_{t}))$. Under these very natural assumptions, we prove that there exists a
$(p/q,l/q)\in \text{int}(\unicode[STIX]{x1D70C}(\widetilde{f}_{t}))$. Under these very natural assumptions, we prove that there exists a 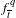 $f_{\overline{t}}^{q}$-fixed hyperbolic saddle
$f_{\overline{t}}^{q}$-fixed hyperbolic saddle 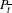 $P_{\overline{t}}$ such that its rotation vector is
$P_{\overline{t}}$ such that its rotation vector is 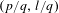 $(p/q,l/q)$. We also prove that there exists a sequence
$(p/q,l/q)$. We also prove that there exists a sequence  $t_{i}>\overline{t}$,
$t_{i}>\overline{t}$, 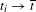 $t_{i}\rightarrow \overline{t}$, such that if
$t_{i}\rightarrow \overline{t}$, such that if 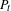 $P_{t}$ is the continuation of
$P_{t}$ is the continuation of 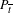 $P_{\overline{t}}$ with the parameter, then
$P_{\overline{t}}$ with the parameter, then 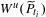 $W^{u}(\widetilde{P}_{t_{i}})$ (the unstable manifold) has quadratic tangencies with
$W^{u}(\widetilde{P}_{t_{i}})$ (the unstable manifold) has quadratic tangencies with 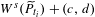 $W^{s}(\widetilde{P}_{t_{i}})+(c,d)$ (the stable manifold translated by
$W^{s}(\widetilde{P}_{t_{i}})+(c,d)$ (the stable manifold translated by 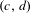 $(c,d)$), where
$(c,d)$), where 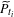 $\widetilde{P}_{t_{i}}$ is any lift of
$\widetilde{P}_{t_{i}}$ is any lift of 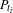 $P_{t_{i}}$ to the plane. In other words,
$P_{t_{i}}$ to the plane. In other words, 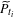 $\widetilde{P}_{t_{i}}$ is a fixed point for
$\widetilde{P}_{t_{i}}$ is a fixed point for  $(\widetilde{f}_{t_{i}})^{q}-(p,l)$, and
$(\widetilde{f}_{t_{i}})^{q}-(p,l)$, and 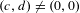 $(c,d)\neq (0,0)$ are certain integer vectors such that
$(c,d)\neq (0,0)$ are certain integer vectors such that 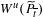 $W^{u}(\widetilde{P}_{\overline{t}})$ do not intersect
$W^{u}(\widetilde{P}_{\overline{t}})$ do not intersect 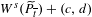 $W^{s}(\widetilde{P}_{\overline{t}})+(c,d)$, and these tangencies become transverse as
$W^{s}(\widetilde{P}_{\overline{t}})+(c,d)$, and these tangencies become transverse as  $t$ increases. We also prove that, for
$t$ increases. We also prove that, for 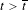 $t>\overline{t}$,
$t>\overline{t}$, 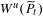 $W^{u}(\widetilde{P}_{t})$ has transverse intersections with
$W^{u}(\widetilde{P}_{t})$ has transverse intersections with 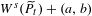 $W^{s}(\widetilde{P}_{t})+(a,b)$, for all integer vectors
$W^{s}(\widetilde{P}_{t})+(a,b)$, for all integer vectors 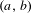 $(a,b)$, and thus one may consider that the tangencies above are associated to the birth of the heteroclinic intersections in the plane that do not exist for
$(a,b)$, and thus one may consider that the tangencies above are associated to the birth of the heteroclinic intersections in the plane that do not exist for 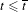 $t\leq \overline{t}$.
$t\leq \overline{t}$.