Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:40:06.390Z Has data issue: false hasContentIssue false
  • English
  • Français

Conjugation between circle maps with several break points

Published online by Cambridge University Press:  21 July 2015

ABDELHAMID ADOUANI
ABDELHAMID ADOUANI*
Affiliation:
University of Carthage, Faculty of Science of Bizerte, Department of Mathematics, Jarzouna 7021, Tunisia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 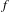$f$ and $g$ be two class $P$ -homeomorphisms of the circle 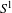$S^{1}$ with break point singularities, which are differentiable maps except at some singular points where the derivative has a jump. Assume that 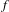$f$ and $g$ have irrational rotation numbers and the derivatives 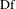$\text{Df}$ and 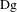$\text{Dg}$ are absolutely continuous on every continuity interval of 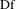$\text{Df}$ and 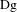$\text{Dg}$ , respectively. We prove that if the product of the 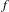$f$ -jumps along all break points of 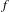$f$ is distinct from that of $g$ then the homeomorphism 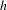$h$ conjugating 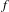$f$ and $g$ is a singular function, i.e. it is continuous on 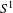$S^{1}$ , but 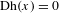$\text{Dh}(x)=0$  almost everywhere with respect to the Lebesgue measure. This result generalizes previous results for one and two break points obtained by Dzhalilov, Akin and Temir, and Akhadkulov, Dzhalilov and Mayer. As a consequence, we get in particular Dzhalilov–Mayer–Safarov’s theorem: if the product of the 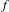$f$ -jumps along all break points of 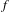$f$ is distinct from $1$ , then the invariant measure 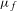$\unicode[STIX]{x1D707}_{f}$ is singular with respect to the Lebesgue measure.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 8 , December 2016 , pp. 2351 - 2383
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adouani, A. and Marzougui, H.. Sur les homéomorphismes du cercle de classe P C r par morceaux (r ≥ 1) qui sont conjugués C r par morceaux aux rotations irrationnelles. Ann. Inst. Fourier (Grenoble) 58 (2008), 755–775.CrossRefGoogle Scholar
Adouani, A. and Marzougui, H.. On piecewise smoothness of conjugacy of class P circle homeomorphisms to diffeomorphisms and rotations. Dyn. Syst. 27 (2012), 169–186.CrossRefGoogle Scholar
Adouani, A. and Marzougui, H.. Singular measures for class P-circle homeomorphisms with several break points. Ergod. Th. & Dynam. Sys. 34 (2014), 423–456.CrossRefGoogle Scholar
Akhadkulov, H., Dzhalilov, A. and Mayer, D.. On conjugations of circle homeomorphisms with two break points. Ergod. Th. & Dynam. Sys. 34 (2014), 725–741.CrossRefGoogle Scholar
Akhadkulov, Kh. A.. Some circle homeomorphisms with break-type singularities. Russian Math. Surveys 61(5) (2006), 981–983.CrossRefGoogle Scholar
de Melo, W. and van Strien, S.. One-Dimensional Dynamics (Ergebnisse der Mathematik und ihrer Grenzgebiete, 25) . Springer, Berlin, 1993.CrossRefGoogle Scholar
Denjoy, A.. Sur les courbes définies par les équations differentielles à la surface du tore. J. Math. Pures Appl. (9) 11 (1932), 333–375.Google Scholar
Dzhalilov, A.. Piecewise smoothness of conjugate homeomorphisms of a circle with corners. Theoret. Math. Phys. 120 (1999), 961–972.CrossRefGoogle Scholar
Dzhalilov, A., Akin, H. and Temir, S.. Conjugations between circle maps with a single break point. J. Math. Anal. Appl. 366 (2010), 1–10.CrossRefGoogle Scholar
Dzhalilov, A. and Khanin, K. M.. On invariant measure for homeomorphisms of a circle with a break point. Funct. Anal. Appl. 32 (1998), 153–161.CrossRefGoogle Scholar
Dzhalilov, A., Liousse, I. and Mayer, D.. Singular measures of piecewise smooth circle homeomorphisms with two break points. Discrete Contin. Dyn. Syst. 24(2) (2009), 381–403.CrossRefGoogle Scholar
Dzhalilov, A., Mayer, D. and Safarov, U. A.. Piecewise-smooth circle homeomorphisms with several break points. Izv. Math. 76 (2012), 94–112.CrossRefGoogle Scholar
Finzi, A.. Sur le problème de la génération d’une transformation donnée d’une courbe fermée par une transformation infinitésimale. Ann. Sci. Éc. Norm. Supér. (3) 67 (1950), 243–305.CrossRefGoogle Scholar
Hasselblatt, B. and Katok, A.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.Google Scholar
Hawkins, J. and Schmidt, K.. On C 2 -diffeomorphisms of the circle which are of type III1. Invent. Math. 66 (1982), 511–518.CrossRefGoogle Scholar
Herman, M.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49 (1979), 5–234.CrossRefGoogle Scholar
Hewitt, E. and Stromberg, K.. Real and Abstract Analysis (Graduate Texts in Mathematics, 25) . Springer, Berlin, 1965.Google Scholar
Katznelson, Y. and Ornstein, D.. The differentiability of the conjugation of certain diffeomorphisms of the circle. Ergod. Th. & Dynam. Sys. 9 (1989), 643–680.CrossRefGoogle Scholar
Khanin, K. and Teplinsky, A.. Renormalization horseshoe and rigidity theory for circle diffeomorphisms with breaks. Comm. Math. Phys. 320 (2013), 347–377.CrossRefGoogle Scholar
Khanin, K. M. and Khmelev, D.. Renormalizations and rigidity theory for circle homeomorphisms with singularities of the break type. Comm. Math. Phys. 235 (2003), 69–124.CrossRefGoogle Scholar
Khanin, K. M. and Sinai, Ya. G.. Smoothness of conjugacies of diffeomorphisms of the circle with rotations. Russian Math. Surveys 44 (1989), 69–99.Google Scholar
Khanin, K. M. and Teplinsky, A.. Herman’s theory revisited. Invent. Math. 178 (2009), 333–344.CrossRefGoogle Scholar
Liousse, I.. Nombre de rotation, mesures invariantes et ratio set des homéomorphismes affines par morceaux du cercle. Ann. Inst. Fourier (Grenoble) 55 (2005), 1001–1052.CrossRefGoogle Scholar
Navas, A.. Groups of Circle Diffeomorphisms (Chicago Lectures in Mathematics) . University of Chicago Press, Chicago, IL, 2011.CrossRefGoogle Scholar
Poincaré, H.. Sur les courbes définies par les équations différentielles. J. Math. Pures Appl. 1 (1885), 167–244.Google Scholar
Sinai, Y. G.. Topics in Ergodic Theory. Princeton University Press, Princeton, NJ, 1994.CrossRefGoogle Scholar
Stark, J.. Smooth conjugacy and renormalisation for diffeomorphisms of the circle. Nonlinearity 1 (1988), 541–575.CrossRefGoogle Scholar
Yoccoz, J. C.. Il n’y a pas de contre-exemple de Denjoy analytique. C. R. Math. Acad. Sci. Paris I 298 (1984), 141–144.Google Scholar