Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T02:30:27.882Z Has data issue: false hasContentIssue false
  • English
  • Français

Complexity of injective piecewise contracting interval maps

Published online by Cambridge University Press:  04 June 2018

E. CATSIGERAS ,
P. GUIRAUD  and
A. MEYRONEINC
E. CATSIGERAS
Affiliation:
Instituto de Matemática y Estadística Rafael Laguardia, Universidad de la República, Montevideo, Uruguay email [email protected]
P. GUIRAUD
Affiliation:
Centro de Investigación y Modelamiento de Fenómenos Aleatorios Valparaíso, Facultad de Ingeniería, Universidad de Valparaíso, Valparaíso, Chile email [email protected]
A. MEYRONEINC
Affiliation:
Departamento de Matemáticas, Instituto Venezolano de Investigaciones Científicas, Apartado 20632, Caracas 1020A, Venezuela email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

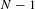We study the complexity of the itineraries of injective piecewise contracting maps on the interval. We prove that for any such map the complexity function of any itinerary is eventually affine. We also prove that the growth rate of the complexity is bounded from above by the number, $N-1$, of discontinuities of the map. To show that this bound is optimal, we construct piecewise affine contracting maps whose itineraries all have the complexity 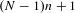$(N-1)n+1$. In these examples, the asymptotic dynamics take place in a minimal Cantor set containing all the discontinuities.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 1 , January 2020 , pp. 64 - 88
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alessandri, P. and Berthé, V.. Three distance theorems and combinatorics on words. Enseign. Math. 44 (1998), 103–132.Google Scholar
Brémont, J.. Dynamics of injective quasi-contractions. Ergod. Th. & Dynam. Sys. 26 (2006), 19–44.10.1017/S0143385705000386Google Scholar
Bugeaud, Y.. Dynamique de certaines applications contractantes linéaires par morceaux sur [0, 1[. C. R. Math. Acad. Sci. Paris, I 317 (1993), 575–578.Google Scholar
Bugeaud, Y. and Conze, J.-P.. Calcul de la dynamique de transformations linéaires contractantes mod 1 et arbre de Farey. Acta Arith. 88 (1999), 201–218.Google Scholar
Catsigeras, E., Guiraud, P., Meyroneinc, A. and Ugalde, E.. On the asymptotic properties of piecewise contracting maps. Dyn. Syst. 67 (2016), 609–655.Google Scholar
Coutinho, R.. Dinâmica simbólica linear. PhD Thesis, Technical University of Lisbon, 1999.Google Scholar
Coutinho, R., Fernandez, B., Lima, R. and Meyroneinc, A.. Discrete time piecewise affine models of genetic regulatory networks. J. Math. Biol. 52 (2006), 524–570.Google Scholar
Didier, G.. Caractérisation des N-écritures et application à l’étude des suites de complexité ultimement n + cste . Theoret. Comput. Sci. 215 (1999), 31–49.Google Scholar
Gambaudo, J.-M. and Tresser, Ch.. On the dynamics of quasi-contractions. Bull. Braz. Math. Soc. (N.S.) 19 (1988), 61–114.Google Scholar
Kruglikov, B. and Rypdal, M.. A piecewise affine contracting map with positive entropy. Discrete Contin. Dyn. Syst. 16 (2006), 393–394.Google Scholar
Lima, R. and Ugalde, E.. Dynamical complexity of discrete-time regulatory networks. Nonlinearity 19 (2006), 237–259.10.1088/0951-7715/19/1/012Google Scholar
Nogueira, A., Pires, B. and Rosales, R.. Asymptotically periodic piecewise contractions of the interval. Nonlinearity 27 (2014), 1603–1610.Google Scholar
Nogueira, A. and Pires, B.. Dynamics of piecewise contractions of the interval. Ergod. Th. & Dynam. Sys. 35 (2015), 2198–2215.10.1017/etds.2014.16Google Scholar
Nogueira, A., Pires, B. and Rosales, R.. Topological dynamics of piecewise 𝜆-affine maps. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2016.104. Published online 10 November 2016.Google Scholar
Pires, B.. Invariant measures for piecewise continuous maps. C. R. Math. Acad. Sci. Paris, I 354 (2016), 717–722.Google Scholar
Veerman, P.. Symbolic dynamics of order-preserving orbits. Physica D 29 (1987), 191–201.10.1016/0167-2789(87)90055-8Google Scholar
Ferenczi, S.. Combinatorial methods for interval exchange transformations. Southeast Asian Bull. Math. 37 (2013), 47–66.Google Scholar
Ferenczi, S. and Zamboni, C.. Languages of k-interval exchange transformations. Bull. Lond. Math. Soc. 40 (2008), 705–714.Google Scholar