Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-27T13:23:48.397Z Has data issue: false hasContentIssue false
  • English
  • Français

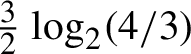A complete proof that square ice entropy is $\tfrac 32\log _{2} (4/3)$

Part of: Equilibrium statistical mechanics Ergodic theory

Published online by Cambridge University Press:  28 April 2022

SILVÈRE GANGLOFF
SILVÈRE GANGLOFF*
Affiliation:
Faculty of Applied Mathematics of AGH, Mickiewicza, A-3/A-4, Krakow, Poland
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this text, we provide a fully rigorous and complete proof of E.H. Lieb’s statement that (topological) entropy of square ice (or six-vertex model, XXZ spin chain for anisotropy parameter 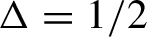$\Delta =1/2$ ) is equal to 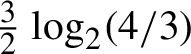$\tfrac 32\log _{2} (4/3)$ .

Keywords

entropysquare icesix-vertex model

MSC classification

Primary: 37A35: Entropy and other invariants, isomorphism, classification
Secondary: 82B20: Lattice systems (Ising, dimer, Potts, etc.) and systems on graphs
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 6 , June 2023 , pp. 1847 - 1908
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baxter, R. J.. Exactly Solved Models in Statistical Mechanics. Academic Press, Cambridge, MA, 1982.Google Scholar
Culik, K.. An aperiodic set of 13 Wang tiles. Discrete Math. 160 (1996), 245–251.CrossRefGoogle Scholar
Duminil-Copin, H., Gagnebin, M., Harel, M., Manolescu, I. and Tassion, V.. Discontinuity of the phase transition for the planar random-cluster and Potts models with q > 4. Preprint, 2017, arXiv:1611.09877.+4.+Preprint,+2017,+arXiv:1611.09877.>Google Scholar
Duminil-Copin, H., Gagnebin, M., Harel, M., Manolescu, I. and Tassion, V.. The Bethe ansatz for the six-vertex and XXZ models: an exposition. Probab. Surv. 15 (2018), 102–130.CrossRefGoogle Scholar
Friedland, S.. On the entropy of ${\mathbb{Z}}^d$ subshifts of finite type. Linear Algebra Appl. 252 (1997), 199–220.CrossRefGoogle Scholar
Friedland, S. and Peled, U. N.. Theory of computation of multidimensional entropy with an application to the monomer-dimer problem. Adv. Appl. Math. 34 (2005), 486–522.CrossRefGoogle Scholar
Gangloff, S. and Sablik, M.. Quantified block gluing, aperiodicity and entropy of multidimensional SFT. J. Anal. Math. 144 (2021), 21–118.CrossRefGoogle Scholar
Hurd, L. P., Kari, J. and Culik, K.. The topological entropy of cellular automata is uncomputable. Ergod. Th. & Dynam. Sys. 12 (1992), 2551–2065.CrossRefGoogle Scholar
Hochman, M. and Meyerovitch, T.. A characterization of the entropies of multidimensional shifts of finite type. Ann. of Math. (2) 171 (2010), 2011–2038.CrossRefGoogle Scholar
Kozlowski, K.. On condensation properties of Bethe roots associated with the XXZ spin chain. Comm. Math. Phys. 357 (2018), 1009–1069.CrossRefGoogle Scholar
Kasteleyn, P. W.. The statistics of dimers on a lattice: I. The number of dimer arrangements on a quadratic lattice. Physica 17 (1961), 1209–1225.CrossRefGoogle Scholar
Kuperberg, G.. Another proof of the alternating sign matrix conjecture. Int. Math. Res. Not. IMRN 1996 (1996), 139–150.CrossRefGoogle Scholar
Lieb, E. H.. Residual entropy of square ice. Phys. Rev. 162 (1967), 162.CrossRefGoogle Scholar
Lind, D. A. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Lieb, E. H., Shultz, T. and Mattis, D.. Two soluble models of an antiferromagnetic chain. Ann. Physics 16 (1961), 407–466.CrossRefGoogle Scholar
Pavlov, R.. Approximating the hard square entropy constant with probabilistic methods. Ann. Probab. 40 (2012), 2362–2399.CrossRefGoogle Scholar
Pavlov, R. and Schraudner, M.. Entropies realizable by block gluing shifts of finite type. J. Anal. Math. 126 (2015), 113–174.CrossRefGoogle Scholar
Pierce, P. A. and Vittori-Orgeas, A.. Yang–Baxter solution of Dimers as a free-fermion six-vertex model. J. Phys. A 50 (2017), 434001.CrossRefGoogle Scholar
Vieira, R. S. and Lima-Santos, A.. The algebraic Bethe ansatz and combinatorial trees. J. Integrable Syst. 4 (2019), xyz002.CrossRefGoogle Scholar
Yang, C. N. and Yang, C. P.. One-dimensional chain of anisotropic spin-spin interactions. I. Proof of Bethe’s hypothesis for ground state in a finite system. Phys. Rev. 150 (1966), 321.CrossRefGoogle Scholar
Yang, C. N. and Yang, C. P.. One-dimensional chain of anisotropic spin-spin interactions. II. Properties of the ground-state energy per lattice site for an infinite system. Phys. Rev. 150 (1966), 327.CrossRefGoogle Scholar