Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:47:27.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Combinatorial and probabilistic properties of systems of numeration

Published online by Cambridge University Press:  16 September 2014

GUY BARAT  and
PETER GRABNER
GUY BARAT
Affiliation:
Institut de Mathématiques de Marseille, Case 907, Université d’Aix-Marseille, 163 avenue de Luminy, 13288 Marseille Cedex 9, France email [email protected]
PETER GRABNER
Affiliation:
Institut für Analysis und Computational Number Theory, Technische Universität Graz, NAWI Graz, Steyrergasse 30, 8010 Graz, Austria email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 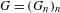$G=(G_{n})_{n}$ be a strictly increasing sequence of positive integers with 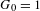$G_{0}=1$. We study the system of numeration defined by this sequence by looking at the corresponding compactification 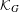${\mathcal{K}}_{G}$ of 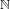$\mathbb{N}$ and the extension of the addition-by-one map ${\it\tau}$ on 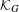${\mathcal{K}}_{G}$ (the ‘odometer’). We give sufficient conditions for the existence and uniqueness of ${\it\tau}$-invariant measures on 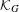${\mathcal{K}}_{G}$ in terms of combinatorial properties of 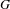$G$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 2 , April 2016 , pp. 422 - 457
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barat, G., Berthé, V., Liardet, P. and Thuswaldner, J.. Dynamical directions in numeration. Ann. Inst. Fourier (Grenoble) 56(7) (2006), 1987–2092.CrossRefGoogle Scholar
Barat, G., Downarowicz, T., Iwanik, A. and Liardet, P.. Propriétés topologiques et combinatoires des échelles de numération. Colloq. Math. 84/85(part 2) (2000), 285–306, Dedicated to the memory of Anzelm Iwanik.CrossRefGoogle Scholar
Barat, G., Downarowicz, T. and Liardet, P.. Dynamiques associées à une échelle de numération. Acta Arith. 103(1) (2002), 41–78.CrossRefGoogle Scholar
Barat, G. and Liardet, P.. Dynamical systems originated in the Ostrowski alpha-expansion. Ann. Univ. Sci. Budapest. Sect. Comput. 24 (2004), 133–184.Google Scholar
Berthé, V. and Rigo, M.. Odometers on regular languages. Theory Comput. Syst. 40(1) (2007), 1–31.CrossRefGoogle Scholar
Bruin, H., Keller, G. and St. Pierre, M.. Adding machines and wild attractors. Ergod. Th. & Dynam. Sys. 17(6) (1997), 1267–1287.CrossRefGoogle Scholar
Carlitz, L., Scoville, R. and Hoggatt, V. E. Jr. Fibonacci representations of higher order I. Fibonacci Quart. 10(1) (1972), 43–69.Google Scholar
Carlitz, L., Scoville, R. and Hoggatt, V. E. Jr. Fibonacci representations of higher order II. Fibonacci Quart. 10(1) (1972), 71–80.Google Scholar
Dooley, A. H.. Markov odometers. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310). Cambridge University Press, Cambridge, 2003, pp. 60–80.CrossRefGoogle Scholar
Doudékova-Puydebois, M.. On dynamics related to a class of numeration systems. Monatsh. Math. 135(1) (2002), 11–24.CrossRefGoogle Scholar
Dumont, J.-M.. Formules sommatoires et systèmes de numération lies aux substitutions. Séminaires de Théor. des Nombres, Bordeaux 16 (1987/88), Exp. Nr. 39, 12 pp.Google Scholar
Dumont, J.-M. and Thomas, A.. Systèmes de numération et fonctions fractales relatifs aux substitutions. Theoret. Comput. Sci. 65 (1989), 153–169.CrossRefGoogle Scholar
Fraenkel, A. S.. Systems of numeration. Amer. Math. Monthly 92 (1985), 105–114.CrossRefGoogle Scholar
Frougny, C.. Fibonacci representations and finite automata. IEEE Trans. Inform. Theory 37 (1991), 393–399.CrossRefGoogle Scholar
Frougny, C.. On the successor function in non-classical numeration systems. Proc. S.T.A.C.S. 96 (Lecture Notes in Computer Science, 1046). Springer, Berlin, 1996, pp. 543–553.Google Scholar
Frougny, C.. On the sequentiality of the successor function. Inform. and Comput. 139 (1997), 17–38.CrossRefGoogle Scholar
Frougny, C.. Number representation and finite automata. Topics in Symbolic Dynamics and Applications (Temuco, 1997) (London Mathematical Society Lecture Notes Series, 279). Cambridge University Press, Cambridge, 2000, pp. 207–228.Google Scholar
Frougny, C.. Numeration systems. Algebraic Combinatorics on Words (Encyclopedia of Mathematics and its Applications, 90). Ed. Lothaire, M.. Cambridge University Press, Cambridge, 2002, pp. 230–268.Google Scholar
Frougny, C.. Non-standard number representation: computer arithmetic, beta-numeration and quasicrystals. Physics and Theoretical Computer Science (NATO Security through Science Series D: Information and Communication Security, 7). IOS, Amsterdam, 2007, pp. 155–169.Google Scholar
Frougny, C. and Solomyak, C.. On representation of integers in linear numerations systems. Ergodic Theory of ℤd-Actions (London Mathematical Society Lecture Note Series, 228). Eds. Pollicott, M. and Schmidt, K.. Cambridge University Press, Cambridge, 1996, pp. 345–368.Google Scholar
Grabner, P. J., Liardet, P. and Tichy, R. F.. Odometers and systems of numeration. Acta Arith. 70 (1995), 103–123.CrossRefGoogle Scholar
Grabner, P. J. and Tichy, R. F.. 𝛼-expansions, linear recurrences and the sum-of-digits function. Manuscripta Math. 70 (1991), 311–324.CrossRefGoogle Scholar
Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis. Springer, Berlin, 1970.Google Scholar
Kátai, I.. Open problems originated in our research work with Zoltán Daróczy. Publ. Math. Debrecen 75 (2009), 149–165.CrossRefGoogle Scholar
Köthe, G.. Topological Vector Spaces. I (Die Grundlehren der Mathematischen Wissenschaften, Band 159). Springer, New York, 1969 (translated from the German by D. J. H. Garling).Google Scholar
Lecomte, P. B. A. and Rigo, M.. Numeration systems on a regular language. Theory Comput. Syst. 34(1) (2001), 27–44.CrossRefGoogle Scholar
Lothaire, M.. Algebraic Combinatorics on Words (Encyclopedia of Mathematics and its Applications, 90). Cambridge University Press, Cambridge, 2002.CrossRefGoogle Scholar
Montgomery, H. L. and Vorhauer, U. M. A.. Greedy sums of distinct squares. Math. Comp. 73(245) (2004), 493–513 (electronic).CrossRefGoogle Scholar
Parry, W.. On the 𝛽-expansions of real numbers. Acta Math. Acad. Sci. Hung. 11 (1960), 401–416.CrossRefGoogle Scholar
Rauzy, G.. Nombres algébriques et substitutions. Bull. Soc. Math. France 110(2) (1982), 147–178.CrossRefGoogle Scholar
Rigo, M.. Automates et systèmes de numération. Bull. Soc. Roy. Sci. Liège 73(5–6) (2005), 257–270.Google Scholar
Schweiger, F.. Ergodic Theory of Fibred Systems and Metric Number Theory. Oxford Science Publications, The Clarendon Press Oxford University Press, New York, 1995.Google Scholar
Sidorov, N.. Arithmetic dynamics. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310). Eds. Bezuglyi, S. and Kolyada, S.. Cambridge University Press, Cambridge, 2003, pp. 145–189.CrossRefGoogle Scholar
Vershik, A. M.. The adic realizations of the ergodic actions with the homeomorphisms of the Markov compact and the ordered Bratteli diagrams. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 223 (1995), 120–126.Google Scholar
Yaglom, A. M. and Yaglom, I. M.. Challenging Mathematical Problems with Elementary Solutions. Vol. II (Problems from Various Branches of Mathematics). Dover Publications Inc, New York, 1987 (translated from the Russian by James McCawley, Jr., Reprint of the 1967 edition).Google Scholar