Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hirsch, Morris W
1989.
Systems of differential equations that are competitive or cooperative. V. Convergence in 3-dimensional systems.
Journal of Differential Equations,
Vol. 80,
Issue. 1,
p.
94.
Hagopian, Charles L.
1993.
Fixed Points of Plane Continua.
Rocky Mountain Journal of Mathematics,
Vol. 23,
Issue. 1,
BenaÏm, Michel
and
Hirsch, Morris W.
1996.
Asymptotic pseudotrajectories and chain recurrent flows, with applications.
Journal of Dynamics and Differential Equations,
Vol. 8,
Issue. 1,
p.
141.
Benaïm, Michel
1999.
Séminaire de Probabilités XXXIII.
Vol. 1709,
Issue. ,
p.
1.
Benaı̈m, Michel
and
Hirsch, Morris W
1999.
Mixed Equilibria and Dynamical Systems Arising from Fictitious Play in Perturbed Games.
Games and Economic Behavior,
Vol. 29,
Issue. 1-2,
p.
36.
Sanchez, Luis A.
2005.
Convergence to equilibria in the Lorenz system via monotone methods.
Journal of Differential Equations,
Vol. 217,
Issue. 2,
p.
341.


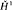 (Λ; ℝ) ≠ 0 if dim
(Λ; ℝ) ≠ 0 if dim