Published online by Cambridge University Press: 03 April 2017
We prove a cocycle superrigidity theorem for a large class of coinduced actions. In particular, if 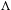 $\unicode[STIX]{x1D6EC}$ is a subgroup of a countable group
$\unicode[STIX]{x1D6EC}$ is a subgroup of a countable group  $\unicode[STIX]{x1D6E4}$, we consider a probability measure preserving action
$\unicode[STIX]{x1D6E4}$, we consider a probability measure preserving action 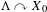 $\unicode[STIX]{x1D6EC}\curvearrowright X_{0}$ and let
$\unicode[STIX]{x1D6EC}\curvearrowright X_{0}$ and let 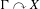 $\unicode[STIX]{x1D6E4}\curvearrowright X$ be the coinduced action. Assume either that
$\unicode[STIX]{x1D6E4}\curvearrowright X$ be the coinduced action. Assume either that  $\unicode[STIX]{x1D6E4}$ has property (T) or that
$\unicode[STIX]{x1D6E4}$ has property (T) or that 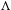 $\unicode[STIX]{x1D6EC}$ is amenable and
$\unicode[STIX]{x1D6EC}$ is amenable and  $\unicode[STIX]{x1D6E4}$ is a product of non-amenable groups. Using Popa’s deformation/rigidity theory we prove
$\unicode[STIX]{x1D6E4}$ is a product of non-amenable groups. Using Popa’s deformation/rigidity theory we prove 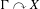 $\unicode[STIX]{x1D6E4}\curvearrowright X$ is
$\unicode[STIX]{x1D6E4}\curvearrowright X$ is 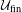 ${\mathcal{U}}_{\text{fin}}$-cocycle superrigid, that is any cocycle for this action to a
${\mathcal{U}}_{\text{fin}}$-cocycle superrigid, that is any cocycle for this action to a 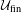 ${\mathcal{U}}_{\text{fin}}$ (e.g. countable) group
${\mathcal{U}}_{\text{fin}}$ (e.g. countable) group 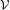 ${\mathcal{V}}$ is cohomologous to a homomorphism from
${\mathcal{V}}$ is cohomologous to a homomorphism from  $\unicode[STIX]{x1D6E4}$ to
$\unicode[STIX]{x1D6E4}$ to 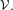 ${\mathcal{V}}.$
${\mathcal{V}}.$