Article contents
A classification of aperiodic order via spectral metrics and Jarník sets
Published online by Cambridge University Press: 13 March 2018
Abstract
Given an 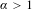 $\unicode[STIX]{x1D6FC}>1$ and a
$\unicode[STIX]{x1D6FC}>1$ and a  $\unicode[STIX]{x1D703}$ with unbounded continued fraction entries, we characterize new relations between Sturmian subshifts with slope
$\unicode[STIX]{x1D703}$ with unbounded continued fraction entries, we characterize new relations between Sturmian subshifts with slope  $\unicode[STIX]{x1D703}$ with respect to (i) an
$\unicode[STIX]{x1D703}$ with respect to (i) an  $\unicode[STIX]{x1D6FC}$-Hölder regularity condition of a spectral metric, (ii) level sets defined in terms of the Diophantine properties of
$\unicode[STIX]{x1D6FC}$-Hölder regularity condition of a spectral metric, (ii) level sets defined in terms of the Diophantine properties of  $\unicode[STIX]{x1D703}$, and (iii) complexity notions which we call
$\unicode[STIX]{x1D703}$, and (iii) complexity notions which we call  $\unicode[STIX]{x1D6FC}$-repetitiveness,
$\unicode[STIX]{x1D6FC}$-repetitiveness,  $\unicode[STIX]{x1D6FC}$-repulsiveness and
$\unicode[STIX]{x1D6FC}$-repulsiveness and  $\unicode[STIX]{x1D6FC}$-finiteness—generalizations of the properties known as linear repetitiveness, repulsiveness and power freeness, respectively. We show that the level sets relate naturally to (exact) Jarník sets and prove that their Hausdorff dimension is
$\unicode[STIX]{x1D6FC}$-finiteness—generalizations of the properties known as linear repetitiveness, repulsiveness and power freeness, respectively. We show that the level sets relate naturally to (exact) Jarník sets and prove that their Hausdorff dimension is 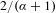 $2/(\unicode[STIX]{x1D6FC}+1)$.
$2/(\unicode[STIX]{x1D6FC}+1)$.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2018
References
- 1
- Cited by


