Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-04T21:31:31.078Z Has data issue: false hasContentIssue false
  • English
  • Français

Characters of inductive limits of finite alternating groups

Part of: Locally compact groups and their algebras

Published online by Cambridge University Press:  04 September 2018

SIMON THOMAS
SIMON THOMAS*
Affiliation:
Mathematics Department, Rutgers University, 110 Frelinghuysen Road, Piscataway, NJ 08854-8019, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

If $G\ncong \operatorname{Alt}(\mathbb{N})$ is an inductive limit of finite alternating groups, then the indecomposable characters of 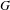$G$ are precisely the associated characters of the ergodic invariant random subgroups of 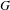$G$.

Keywords

alternating groupscharactersgroup actions

MSC classification

Primary: 22D40: Ergodic theory on groups
Secondary: 22D10: Unitary representations of locally compact groups
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 4 , April 2020 , pp. 1068 - 1082
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abért, M., Glasner, Y. and Virag, B.. Kesten’s theorem for invariant random subgroups. Duke Math. J. 163 (2014), 465–488.Google Scholar
Choksi, J. R.. Inverse limits of measure spaces. Proc. Lond. Math. Soc. (3) 8 (1958), 321–342.Google Scholar
Conley, C., Kechris, A. S. and Tucker-Drob, R.. Ultraproducts of measure preserving actions and graph combinatorics. Ergod. Th. & Dynam. Sys. 33 (2013), 334–374.Google Scholar
Creutz, D. and Peterson, J.. Stabilizers of ergodic actions of lattices and commensurators. Trans. Amer. Math. Soc. 369 (2017), 4119–4166.Google Scholar
Hall, J. I.. Infinite alternating groups as finitary linear transformation groups. J. Algebra 119 (1988), 337–359.Google Scholar
Leinen, F. and Puglisi, O.. Diagonal limits of finite alternating groups: confined subgroups, ideals, and positive definite functions. Illinois J. Math. 47 (2003), 345–360.Google Scholar
Leinen, F. and Puglisi, O.. Positive definite functions of diagonal limits of finite alternating groups. J. Lond. Math. Soc. (2) 70 (2004), 678–690.Google Scholar
Lindenstrauss, E.. Pointwise theorems for amenable groups. Electron. Res. Announc. Amer. Math. Soc. 5 (1999), 82–90.Google Scholar
Loeb, P. A.. Conversion from nonstandard to standard measure spaces and applications in probability theory. Trans. Amer. Math. Soc. 211 (1975), 113–122.Google Scholar
Peterson, J. and Thom, A.. Character rigidity for special linear groups. J. Reine Angew. Math. 716 (2016), 207–228.Google Scholar
Roichman, Y.. Upper bound on the characters of the symmetric groups. Invent. Math. 125 (1996), 451–485.Google Scholar
Sagan, B. E.. The Symmetric Group: Representations, Combinatorial Algorithms, and Symmetric Functions (Graduate Texts in Mathematics, 203). Springer, New York, 2001.Google Scholar
Thoma, E.. Über unitäre Darstellungen abzählbarer, diskreter Gruppen. Math. Ann. 153 (1964), 111–138.Google Scholar
Thoma, E.. Die unzerlegbaren, positiv-definiten Klassenfunktionen der abzählbar unendlichen, symmetrischen Gruppe. Math. Z. 85 (1964), 40–61.Google Scholar
Thomas, S. and Tucker-Drob, R.. Invariant random subgroups of inductive limits of finite alternating groups. J. Algebra 503 (2018), 474–533.Google Scholar
Vershik, A. M.. Nonfree actions of countable groups and their characters. J. Math. Sci. (N.Y.) 174 (2011), 1–6.Google Scholar
Vershik, A. M.. Totally nonfree actions and the infinite symmetric group. Mosc. Math. J. 12 (2012), 193–212.Google Scholar
Vershik, A. M. and Kerov, S. V.. Locally semisimple algebras. Combinatorial theory and the K-functor. J. Sov. Math. 38 (1987), 1701–1733.Google Scholar
Zalesskii, A. E.. Group rings of inductive limits of alternating groups. Leningrad Math. J. 2 (1991), 1287–1303.Google Scholar