Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T00:32:55.432Z Has data issue: false hasContentIssue false
  • English
  • Français

Central sets generated by uniformly recurrent words

Published online by Cambridge University Press:  11 October 2013

MICHELANGELO BUCCI ,
SVETLANA PUZYNINA  and
LUCA Q. ZAMBONI
MICHELANGELO BUCCI
Affiliation:
Department of Mathematics, University of Turku, FIN-20014 Turku, Finland email [email protected]@utu.fi
SVETLANA PUZYNINA
Affiliation:
Department of Mathematics, University of Turku, FIN-20014 Turku, Finland email [email protected]@utu.fi Sobolev Institute of Mathematics, 4 Acad. Koptyug Avenue, 630090 Novosibirsk, Russia
LUCA Q. ZAMBONI
Affiliation:
Department of Mathematics, University of Turku, FIN-20014 Turku, Finland email [email protected]@utu.fi Université de Lyon, Université Lyon 1, CNRS UMR 5208, Institut Camille Jordan, 43 Boulevard du 11 novembre 1918, F-69622 Villeurbanne Cedex, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A subset 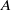$A$ of 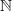$ \mathbb{N} $ is called an IP-set if 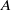$A$ contains all finite sums of distinct terms of some infinite sequence 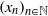$\mathop{({x}_{n} )}\nolimits_{n\in \mathbb{N} } $ of natural numbers. Central sets, first introduced by Furstenberg using notions from topological dynamics, constitute a special class of IP-sets possessing rich combinatorial properties: each central set contains arbitrarily long arithmetic progressions and solutions to all partition regular systems of homogeneous linear equations. In this paper we investigate central sets in the framework of combinatorics on words. Using various families of uniformly recurrent words, including Sturmian words, the Thue–Morse word and fixed points of weak mixing substitutions, we generate an assortment of central sets which reflect the rich combinatorial structure of the underlying words. The results in this paper rely on interactions between different areas of mathematics, some of which have not previously been directly linked. They include the general theory of combinatorics on words, abstract numeration systems, and the beautiful theory, developed by Hindman, Strauss and others, linking IP-sets and central sets to the algebraic/topological properties of the Stone-Čech compactification of 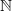$ \mathbb{N} $.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 3 , May 2015 , pp. 714 - 736
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnoux, P. and Rauzy, G.. Représentation géométrique de suites de complexité $2n+ 1$. Bull. Soc. Math. France 119 (1991), 199–215.Google Scholar
Auslander, J.. Minimal Flows and their Extensions (North-Holland Mathematical Studies, 153). North-Holland, Amsterdam, 1988.Google Scholar
Baker, V., Barge, M. and Kwapisz, J.. Geometric realization and coincidence for reducible non-unimodular Pisot tiling spaces with an application to $\beta $-shifts. Ann. Inst. Fourier (Grenoble) 56 (7) (2006), 2213–2248.Google Scholar
Bergelson, V.. Minimal idempotents and ergodic Ramsey theory. Topics in Dynamics and Ergodic Theory (London Mathematics Society Lecture Note Series, 310). Cambridge University Press, Cambridge, 2003, pp. 8–39.Google Scholar
Bergelson, V. and Hindman, N.. Nonmetrizable topological dynamics and Ramsey theory. Trans. Amer. Math. Soc. 320 (1990), 293–320.CrossRefGoogle Scholar
Bergelson, V., Hindman, N. and Strauss, D.. Strongly central sets and sets of polynomial returns mod 1. Proc. Amer. Math. Soc. 140 (2012), 2671–2686.Google Scholar
Blass, A.. Ultrafilters: where topological dynamics $= $ algebra $= $ combinatorics. Topology Proc. 18 (1993), 33–56.Google Scholar
Bucci, M., Hindman, N., Puzynina, S. and Zamboni, L. Q.. On additive properties of sets defined by the Thue–Morse word. J. Combin. Theory Ser. A 120 (2013), 1235–1245.Google Scholar
Cassaigne, J., Ferenczi, S. and Zamboni, L. Q.. Imbalances in Arnoux-Rauzy sequences. Ann. Inst. Fourier (Grenoble) 50 (4) (2000), 1265–1276.Google Scholar
De, D., Hindman, N. and Strauss, D.. A new and stronger central sets theorem. Fund. Math. 199 (2008), 155–175.CrossRefGoogle Scholar
Dekking, F. M. and Keane, M.. Mixing properties of substitutions. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 42 (1978), 23–33.Google Scholar
de Luca, A.. Sturmian words: structure, combinatorics, and their arithmetics. Theoret. Comput. Sci. 183 (1997), 45–82.Google Scholar
Dumont, J.-M. and Thomas, A.. Systèmes de numération et fonctions fractales relatifs aux substitutions. Theoret. Comput. Sci. 65 (2) (1989), 153–169.Google Scholar
Dumont, J.-M. and Thomas, A.. Digital sum moments and substitutions. Acta Arith. 64 (1993), 205–225.CrossRefGoogle Scholar
Edson, M. and Zamboni, L. Q.. On the number of partitions of an integer in the $m$-bonacci base. Ann. Inst. Fourier (Grenoble) 56 (7) (2006), 2271–2283.Google Scholar
Ellis, R.. Distal transformation groups. Pacific J. Math. 8 (1958), 401–405.Google Scholar
Fon-Der-Flaass, D. G. and Frid, A. E.. On periodicity and low complexity of infinite permutations. European J. Combin. 28 (2007), 2106–2114.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.CrossRefGoogle Scholar
Hindman, N.. Finite sums of sequences within cells of a partition of $ \mathbb{N} $. J. Combin. Theory Ser. A 17 (1974), 1–11.Google Scholar
Hindman, N.. Ultrafilters and Ramsey theory: an update. Set Theory and its Applications (Lecture Notes in Mathematics, 1401). Eds. Steprans, J. and Watson, S.. Springer, Berlin, 1989, pp. 97–118.Google Scholar
Hindman, N., Leader, I. and Strauss, D.. Infinite partition regular matrices: solutions in central sets. Trans. Amer. Math. Soc. 355 (2003), 1213–1235.CrossRefGoogle Scholar
Hindman, N. and Strauss, D.. Algebra in the Stone-Čech Compactification. Theory and Applications (de Gruyter Expositions in Mathematics, 27). Walter de Gruyter & Co., Berlin, 1998.Google Scholar
Hindman, N. and Strauss, D.. A simple characterization of sets satisfying the Central Sets Theorem. New York J. Math. 15 (2009), 405–413.Google Scholar
Kamae, T.. Uniform sets and super-stationary sets over general alphabets. Ergodic Th. & Dynam. Sys. 31 (2011), 1445–1461.CrossRefGoogle Scholar
Kamae, T.. Behavior of various complexity functions. Theoret. Comput. Sci. 420 (2012), 36–47.CrossRefGoogle Scholar
Lothaire, M.. Algebraic Combinatorics on Words. Cambridge University Press, Cambridge, 2002.CrossRefGoogle Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics II: Sturmian trajectories. Amer. J. Math. 62 (1) (1940), 1–42.Google Scholar
Zeckendorff, E.. Représentation des nombres naturels par une somme de nombres de Fibonacci ou de nombres de Lucas. Bull. Soc. Roy. Sci. Liège 42 (1972), 179–182.Google Scholar