Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T14:56:05.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Cantor sets of circles of Sierpiński curve Julia sets

Published online by Cambridge University Press:  01 October 2007

ROBERT L. DEVANEY
ROBERT L. DEVANEY*
Affiliation:
Department of Mathematics, Boston University, 111 Cummington Street, Boston, MA 02215, USA (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Our goal in this paper is to give an example of a one-parameter family of rational maps for which, in the parameter plane, there is a Cantor set of simple closed curves consisting of parameters for which the corresponding Julia set is a Sierpiński curve. Hence, the Julia sets for each of these parameters are homeomorphic. However, each of the maps in this set is dynamically distinct from (i.e. not topologically conjugate to) any other map in this set (with only finitely many exceptions). We also show that, in the dynamical plane for any map drawn from a large open set in the connectedness locus in this family, there is a Cantor set of invariant simple closed curves on which the map is conjugate to the product of certain subshifts of finite type with the maps 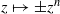on the unit circle.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 27 , Issue 5 , October 2007 , pp. 1525 - 1539
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Blanchard, P., Devaney, R. L., Look, D. M., Seal, P. and Shapiro, Y.. Sierpiński curve Julia sets and singular perturbations of complex polynomials. Ergod. Th. & Dynam. Sys. 25 (2005), 1047–1055.CrossRefGoogle Scholar
[2]Devaney, R. L.. Cantor necklaces and structurally unstable Sierpiński curve Julia sets for rational maps. Qual. Theory Dyn. Syst. 5 (2006), 337–359.CrossRefGoogle Scholar
[3]Devaney, R. L.. Structure of the McMullen domain in the parameter planes for rational maps. Fund. Math. 185 (2005), 267–285.CrossRefGoogle Scholar
[4]Devaney, R. L.. A myriad of Sierpiński curve Julia sets. Proc. Conf. on Difference Equations, Special Functions, and Applications. World Scientific, Singapore, 2007, pp. 87–99.Google Scholar
[5]Devaney, R. L. and Marotta, S.. The McMullen domain: rings around the boundary. Trans. Amer. Math. Soc. to appear.Google Scholar
[6]Devaney, R. L. and Look, D. M.. A criterion for Sierpiński curve Julia sets. Topology Proc. 30 (2006), 163–179.Google Scholar
[7]Devaney, R. L., Look, D. M. and Uminsky, D.. The escape trichotomy for singularly perturbed rational maps. Indiana Univ. Math. J. 54 (2005), 1621–1634.CrossRefGoogle Scholar
[8]Hawkins, J. and Look, D. M.. Locally Sierpiński Julia sets of Weierstrass elliptic functions. Internat. J. Bifur. Chaos Appl. Sci. Engrg. to appear.Google Scholar
[9]McMullen, C.. Automorphisms of rational maps. Holomorphic Functions and Moduli Vol. 1 (Math. Sci. Res. Inst. Publ., 10). Springer, New York, 1988.Google Scholar
[10]Milnor, J.. Dynamics in One Complex Variable. Vieweg, Braunschweig, 1999.Google Scholar
[11]Milnor, J. and Tan, L.. A ‘Sierpiński Carpet’ as Julia set. Appendix F in ‘Geometry and dynamics of quadratic rational maps’. Experiment. Math. 2 (1993), 37–83.CrossRefGoogle Scholar
[12]Petersen, C. and Ryd, G.. Convergence of rational rays in parameter spaces. The Mandelbrot Set: Theme and Variations (London Mathematical Society, Lecture Note Series, 274). Cambridge University Press, Cambridge, 2000, pp. 161–172.CrossRefGoogle Scholar
[13]Roesch, P.. On capture zones for the family f λ(z)=z 2+λ/z 2. Dynamics on the Riemann Sphere. Eds. P. Horth and C. Petersen. European Mathematical Society, Helsinki, 2006, pp. 121–129.CrossRefGoogle Scholar
[14]Yongcheng, Y.. On the Julia set of semi-hyperbolic rational maps. Chinese J. Contemp. Math. 20 (1999), 469–476.Google Scholar
[15]Whyburn, G. T.. Topological characterization of the Sierpiński curve. Fund. Math. 45 (1958), 320–324.CrossRefGoogle Scholar
[16]Wittner, B.. On the bifurcation loci of rational maps of degree two. PhD Thesis, Cornell University.Google Scholar