Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T15:32:55.692Z Has data issue: false hasContentIssue false
  • English
  • Français

C*-algebras of a Cantor system with finitely many minimal subsets: structures, K-theories, and the index map

Part of: Selfadjoint operator algebras Topological dynamics

Published online by Cambridge University Press:  20 February 2020

SERGEY BEZUGLYI ,
ZHUANG NIU  and
WEI SUN
SERGEY BEZUGLYI
Affiliation:
University of Iowa, Iowa City, IA 52242, USA email [email protected]
ZHUANG NIU
Affiliation:
Department of Mathematics, University of Wyoming, Laramie, WY82071, USA email [email protected]
WEI SUN
Affiliation:
Department of Mathematics, East China Normal University, Shanghai 200062, China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study homeomorphisms of a Cantor set with 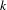$k$ (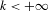$k<+\infty$) minimal invariant closed (but not open) subsets; we also study crossed product C*-algebras associated to these Cantor systems and certain of their orbit-cut sub-C*-algebras. In the case where 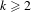$k\geq 2$, the crossed product C*-algebra is stably finite, has stable rank 2, and has real rank 0 if in addition 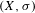$(X,\unicode[STIX]{x1D70E})$ is aperiodic. The image of the index map is connected to certain directed graphs arising from the Bratteli–Vershik–Kakutani model of the Cantor system. Using this, it is shown that the ideal of the Bratteli diagram (of the Bratteli–Vershik–Kakutani model) must have at least 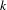$k$ vertices at each level, and the image of the index map must consist of infinitesimals.

Keywords

operator algebrastopological dynamicsK-theoryCantor systemsindex map

MSC classification

Primary: 46L35: Classifications of $C^*$-algebras 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 5 , May 2021 , pp. 1296 - 1341
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bezuglyi, S., Dooley, A. H. and Kwiatkowski, J.. Topologies on the group of homeomorphisms of a Cantor set. Topol. Methods Nonlinear Anal. 27(2) (2006), 299–331.Google Scholar
Bezuglyi, S., Dooley, A. H. and Medynets, K.. The Rokhlin lemma for homeomorphisms of a Cantor set. Proc. Amer. Math. Soc. 133(10) (2005), 2957–2964.CrossRefGoogle Scholar
Bezuglyi, S. and Karpel, O.. Bratteli diagrams: structure, measures, dynamics. Dynamics and Numbers (Contemporary Mathematics, 669) . American Mathematical Society, Providence, RI, 2016, pp. 1–36.Google Scholar
Bezuglyi, S., Kwiatkowski, J. and Medynets, K.. Aperiodic substitution systems and their Bratteli diagrams. Ergod. Th. & Dynam. Sys. 29(1) (2009), 37–72.CrossRefGoogle Scholar
Bezuglyi, S., Kwiatkowski, J., Medynets, K. and Solomyak, B.. Finite rank Bratteli diagrams: structure of invariant measures. Trans. Amer. Math. Soc. 365(5) (2013), 2637–2679.CrossRefGoogle Scholar
Bezuglyi, S., Kwiatkowski, J. and Yassawi, R.. Perfect orderings on finite rank Bratteli diagrams. Canad. J. Math. 66(1) (2014), 57–101.Google Scholar
Bezuglyi, S. and Yassawi, R.. Orders that yield homeomorphisms on Bratteli diagrams. Dyn. Syst. 32(2) (2017), 249–282.CrossRefGoogle Scholar
Bratteli, O.. Inductive limits of finite dimensional C*-algebras. Trans. Amer. Math. Soc. 171 (1972), 195–234.Google Scholar
Cornfeld, I. P., Fomin, S. V. and Sinaĭ, Y. G.. Ergodic Theory (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 245) . Springer, New York, 1982. Translated from the Russian by A. B. Sosinskiĭ.Google Scholar
Davidson, K. R.. C*-Algebras by Example (Fields Institute Monographs, 6) . American Mathematical Society, Providence, RI, 1996.CrossRefGoogle Scholar
Downarowicz, T. and Karpel, O.. Dynamics in dimension zero: a survey. Discrete Contin. Dyn. Syst. 38(3) (2018), 1033–1062.Google Scholar
Durand, F.. Combinatorics on Bratteli diagrams and dynamical systems. Combinatorics, Automata and Number Theory (Encyclopedia of Mathematics and its Applications, 135) . Cambridge University Press, Cambridge, 2010, pp. 324–372.CrossRefGoogle Scholar
Elliott, G. A.. Automorphisms determined by multipliers on ideals of a C*-algebra. J. Funct. Anal. 23(1) (1976), 1–10.CrossRefGoogle Scholar
Elliott, G. A.. On the classification of inductive limits of sequences of semisimple finite-dimensional algebras. J. Algebra 38(1) (1976), 29–44.CrossRefGoogle Scholar
Giordano, T., Putnam, I. F. and Skau, C. F.. Topological orbit equivalence and C*-crossed products. J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Glasner, E. and Weiss, B.. Topological groups with Rokhlin properties. Colloq. Math. 110(1) (2008), 51–80.CrossRefGoogle Scholar
Goodearl, K. R.. Partially Ordered Abelian Groups with Interpolation (Mathematical Surveys and Monographs, 20) . American Mathematical Society, Providence, RI, 1986.Google Scholar
Herman, R. H., Putnam, I. F. and Skau, C. F.. Ordered Bratteli diagrams, dimension groups and topological dynamics. Internat. J. Math. 3(6) (1992), 827–864.CrossRefGoogle Scholar
Hjelmborg, J. v. B. and Rørdam, M.. On stability of C ∗ -algebras. J. Funct. Anal. 155(1) (1998), 153–170.CrossRefGoogle Scholar
Hochman, M.. Genericity in topological dynamics. Ergod. Th. & Dynam. Sys. 28(1) (2008), 125–165.CrossRefGoogle Scholar
Janssen, J., Quas, A. and Yassawi, R.. Bratteli diagrams where random orders are imperfect. Proc. Amer. Math. Soc. 145(2) (2017), 721–735.CrossRefGoogle Scholar
Lin, H. and Rørdam, M.. Extensions of inductive limits of circle algebras. J. Lond. Math. Soc. (2) 51 (1995), 603–613.CrossRefGoogle Scholar
Medynets, K.. Cantor aperiodic systems and Bratteli diagrams. C. R. Math. Acad. Sci. Paris 342(1) (2006), 43–46.Google Scholar
Medynets, K.. On approximation of homeomorphisms of a Cantor set. Fund. Math. 194(1) (2007), 1–13.CrossRefGoogle Scholar
Pimsner, M.. Embedding some transformation group C*-algebras into AF-algebras. Ergod. Th. & Dynam. Sys. 3(4) (1983), 613–626.CrossRefGoogle Scholar
Poon, Y. T.. Stable rank of some crossed product C*-algebras. Proc. Amer. Math. Soc. 105(4) (1989), 868–875.Google Scholar
Poon, Y. T.. AF subalgebras of certain crossed products. Rocky Mountain J. Math. 20(2) (1990), 527–537.Google Scholar
Putnam, I. F.. The C*-algebras associated with minimal homeomorphisms of the Cantor set. Pacific J. Math. 136(2) (1989), 329–353.Google Scholar
Putnam, I. F.. On the topological stable rank of certain transformation group C*-algebras. Ergod. Th. & Dynam. Sys. 10(1) (1990), 197–207.CrossRefGoogle Scholar
Rieffel, M. A.. Dimension and stable rank in the K-theory of C*-algebras. Proc. Lond. Math. Soc. (3) 46(2) (1983), 301–333.Google Scholar
Rørdam, M., Larsen, F. and Laustsen, N. J.. An Introduction to K-Theory for C*-Algebras (London Mathematical Society Student Texts, 49) . Cambridge University Press, Cambridge, 2000.CrossRefGoogle Scholar