Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-13T08:31:37.423Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcation and chain recurrence

Published online by Cambridge University Press:  19 September 2008

M. Hurley
M. Hurley
Affiliation:
Department of Mathematics, Case Western Reserve University, Cleveland, Ohio 44106, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that there is a residual subset of the set of C1 diffeomorphisms on any compact manifold at which the map

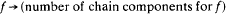
is continuous. As this number is apt to be infinite, we prove a localized version, which allows one to conclude that if f is in this residual set and X is an isolated chain component for f, then

(i) there is a neighbourhood U of X which isolates it from the rest of the chain recurrent set of f, and

(ii) all g sufficiently C1 close to f have precisely one chain component in U, and these chain components approach X as g approaches f.

(ii) is interpreted as a generic non-bifurcation result for this type of invariant set.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 3 , Issue 2 , June 1983 , pp. 231 - 240
Copyright
Copyright © Cambridge University Press 1983

References

REFERENCES

[1]Conley, C.. Isolated Invariant Sets and the Morse Index. Amer. Math. Soc.: Providence, 1978.CrossRefGoogle Scholar
[2]Hirsch, M.. Differential Topology. Springer-Verlag: New York, 1976.CrossRefGoogle Scholar
[3]Hurley, M.. Attractors: persistence, and density of their basins. Trans. Amer. Math. Soc. 269 (1982), 247–271.CrossRefGoogle Scholar
[4]Nadler, S.. Hyperspaces of Sets. Marcel Dekker: New York, 1978.Google Scholar
[5]Newhouse, S.. Diffeomorphisms with infinitely many sinks. Topology. 13 (1974), 9–18.CrossRefGoogle Scholar
[6]Nitecki, Z.. Differentiable Dynamics. M.I.T. Press: Cambridge, 1971.Google Scholar
[7]Pugh, C.. The closing lemma. Amer. J. of Math. 89 (1967), 956–1009.CrossRefGoogle Scholar
[8]Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.CrossRefGoogle Scholar
[9]Takens, F.. On Zeeman's tolerance stability conjecture. Manifolds-Amsterdam, 1970, Springer Lecture Notes in Math. No. 197. Springer-Verlag: New York, 1971.Google Scholar
[10]Takens, F.. Tolerance stability. Dynamical Systems-Warwick, 1974, Springer Lecture Notes in Math. No. 468, pp. 293–304. Springer-Verlag: New York, 1975.CrossRefGoogle Scholar