Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T16:10:32.042Z Has data issue: false hasContentIssue false
  • English
  • Français

Basic dynamical stability results for

Published online by Cambridge University Press:  01 June 2008

JOHN W. ROBERTSON
JOHN W. ROBERTSON*
Affiliation:
Department of Mathematics and Statistics, Wichita State University, Wichita, KS 67260-0033, USA (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study stability questions for dynamics on using holomorphic families, which we require to be locally simply parameterized. Given such a holomorphic family 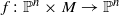, we define the notion of a ‘Fatou section’, which is intuitively a choice of one point in for each map in the family such that: (1) the chosen point depends holomorphically on M, and (2) the points chosen for two different maps behave dynamically ‘comparably’ under iteration of those respective maps. We prove a weak version of the λ-lemma for dynamical systems on by showing that the set of all Fatou sections is a compact space. We introduce the notion of a postcritically bounded holomorphic family and show that if a (locally simply parameterized) holomorphic family is postcritically bounded by some open subset of then: (1) repelling periodic points in the Julia set for one member of the family cannot bifurcate, nor can they leave the Julia set in other members of the family, (2) there is a Fatou section which never leaves the Julia set through each point of the Julia set of any member of the family, and (3) any intersection between the Julia set and the critical set is persistent, in the sense that there is a Fatou section through the point of intersection which never leaves either the critical set or the Julia set. Here, for conciseness, we are using the term ‘Julia set’ to mean the support of the unique measure of maximal entropy, although we recognize that how this term should be used in higher dimensions is still undecided. We also provide a brief summary of the development of the field in our introduction.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 3 , June 2008 , pp. 947 - 977
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Briend, J.-Y. and Duval, J.. Exposants de Liapounoff et distribution des points périodiques d’un endomorphisme de . Acta Math. 182(2) (1999), 143–157.CrossRefGoogle Scholar
[2]Briend, J.-Y. and Duval, J.. Deux caractérisations de la mesure d’équilibre d’un endomorphisme de pk(C). Publ. Math. Inst. Hautes Études Sci. 93 (2001), 145–159.CrossRefGoogle Scholar
[3]Buzzard, G. T., Lynch Hruska, S. and Ilyashenko, Y.. Kupka–Smale theorem for polynomial automorphisms of and persistence of heteroclinic intersections. Invent. Math. 161(1) (2005), 45–89.CrossRefGoogle Scholar
[4]Bedford, E., Lyubich, M. and Smillie, J.. Distribution of periodic points of polynomial diffeomorphisms of . Invent. Math. 114(2) (1993), 277–288.CrossRefGoogle Scholar
[5]Bedford, E., Lyubich, M. and Smillie, J.. Polynomial diffeomorphisms of . IV. The measure of maximal entropy and laminar currents. Invent. Math. 112(1) (1993), 77–125.CrossRefGoogle Scholar
[6]Brolin, H.. Invariant sets under iteration of rational functions. Ark. Mat. 6 (1965), 103–144.CrossRefGoogle Scholar
[7]Bedford, E. and Smillie, J.. Polynomial diffeomorphisms of : currents, equilibrium measure and hyperbolicity. Invent. Math. 103(1) (1991), 69–99.CrossRefGoogle Scholar
[8]Bedford, E. and Smillie, J.. Polynomial diffeomorphisms of . III. Ergodicity, exponents and entropy of the equilibrium measure. Math. Ann. 294(3) (1992), 395–420.CrossRefGoogle Scholar
[9]Bedford, E. and Smillie, J.. Polynomial diffeomorphisms of . V. Critical points and Lyapunov exponents. J. Geom. Anal. 8(3) (1998), 349–383.CrossRefGoogle Scholar
[10]Bedford, E. and Smillie, J.. Polynomial diffeomorphisms of . VI. Connectivity of J. Ann. of Math. (2) 148(2) (1998), 695–735.CrossRefGoogle Scholar
[11]Bedford, E. and Smillie, J.. Polynomial diffeomorphisms of . VII. Hyperbolicity and external rays. Ann. Sci. École Norm. Sup. (4) 32(4) (1999), 455–497.CrossRefGoogle Scholar
[12]Bedford, E. and Smillie, J.. Polynomial diffeomorphisms of . VIII. Quasi-expansion. Amer. J. Math. 124(2) (2002), 221–271.CrossRefGoogle Scholar
[13]Buzzard, G.. Nondensity of stability for polynomial automorphisms of . Indiana Univ. Math. J. 48(3) (1999), 857–865.CrossRefGoogle Scholar
[14]Buzzard, G. and Verma, K.. Hyperbolic automorphisms and holomorphic motions in . Mich. Math. J. 49(3) (2001), 541–565.CrossRefGoogle Scholar
[15]Cantat, S.. Dynamique des automorphismes des surfaces K3. Acta Math. 187(1) (2001), 1–57.CrossRefGoogle Scholar
[16]Diller, J. and Favre, C.. Dynamics of bimeromorphic maps of surfaces. Amer. J. Math. 123(6) (2001), 1135–1169.CrossRefGoogle Scholar
[17]Douady, A. and Hubbard, J. H.. Étude dynamique des polynômes complexes. Partie I (Publications Mathématiques d’Orsay, 84). Université de Paris-Sud, Département de Mathématiques, Orsay, 1984.Google Scholar
[18]Dinh, T.-C. and Sibony, N.. Dynamics des applications d’allure polynomiale. J. Math. Pures Appl. (9) 82(4) (2003), 367–423.CrossRefGoogle Scholar
[19]Dinh, T.-C. and Sibony, N.. Green currents for holomorphic automorphisms of compact Kähler manifolds. J. Amer. Math. Soc. 18(2) (2005), 291–312.CrossRefGoogle Scholar
[20]Favre, C. and Jonsson, M.. Brolin’s theorem for curves in two complex dimensions. Ann. Inst. Fourier 53 (2003), 1461–1501.CrossRefGoogle Scholar
[21]Friedland, S. and Milnor, J.. Dynamical properties of plane polynomial automorphisms. Ergod. Th. & Dynam. Sys. 9(1) (1989), 67–99.CrossRefGoogle Scholar
[22]Fornaess, J. E.. Dynamics in Several Complex Variables (Regional Conference Series in Mathematics, 87). American Mathematical Society, Providence, RI, 1996.Google Scholar
[23]Fornaess, J. E. and Sibony, N.. Complex Hénon mappings in and Fatou–Bieberbach domains. Duke Math. J. 65(2) (1992), 345–380.CrossRefGoogle Scholar
[24]Fornaess, J. E. and Sibony, N.. Complex dynamics in higher dimension. I. Astérisque 222 (1994), 201–231.Google Scholar
[25]Fornaess, J. E. and Sibony, N.. Complex dynamics in higher dimension. II. Modern Methods in Complex Analysis (Princeton, NJ, 1992). Princeton University Press, Princeton, NJ, 1995, pp. 135–182.Google Scholar
[26]Grauert, H. and Remmert, R.. Coherent Analytic Sheaves. Springer-Verlag, Berlin, 1984.CrossRefGoogle Scholar
[27]Hubbard, J. H. and Oberste-Vorth, R. W.. Hénon mappings in the complex domain. II. Projective and inductive limits of polynomials. Real and Complex Dynamical Systems (Hillerød, 1993) (NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 464). Kluwer Academic, Dordrecht, 1995, pp. 89–132.CrossRefGoogle Scholar
[28]Hubbard, J. H. and Papadopol, P.. Superattractive fixed points in . Indiana Univ. Math. J. 43(1) (1994), 321–365.CrossRefGoogle Scholar
[29]Jonsson, M.. Holomorphic motions of hyperbolic sets. Michigan Math. J. 45(2) (1998), 409–415.CrossRefGoogle Scholar
[30]Jonsson, M. and Weickert, B.. A nonalgebraic attractor in . Proc. Amer. Math. Soc. 128(10) (2000), 2999–3002.CrossRefGoogle Scholar
[31]Khenkin, G. M. (ed.), Algebraic aspects of complex analysis (Several Complex Variables, IV). Springer, Berlin, 1990. A translation of Sovremennye problemy matematiki. Fundamentalnye napravleniya, vol. 10, Akad. Nauk SSSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1986 [MR 87m:32003], Translation by J. Leiterer and J. Nunemacher, Translation edited by S. G. Gindikin and G. M. Khenkin.Google Scholar
[32]Laĭterer, Yu.. Holomorphic Vector Bundles and the Oka–Grauert Principle (Current Problems in Mathematics. Fundamental Directions, 10). Akad. Nauk SSSR Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1986, pp. 75–121, 283 (in Russian). Translated by D. N. Akhiezer.Google Scholar
[33]Lyubich, M. and Robertson, J.. The critical locus and rigidity of foliations of complex Hénon maps. Preprint.Google Scholar
[34]Lyubich, M. Yu.. Some typical properties of the dynamics of rational mappings. Uspekhi Mat. Nauk 38(5/233) (1983), 197–198.Google Scholar
[35]Maegawa, K.. On Fatou maps into compact complex manifolds. Ergod. Th. & Dynam. Sys. 25(5) (2005), 1551–1560.CrossRefGoogle Scholar
[36]McMullen, C. T.. Dynamics on K3 surfaces: Salem numbers and Siegel disks. J. reine angew. Math. 545 (2002), 201–233.Google Scholar
[37]Mañé, R., Sad, P. and Sullivan, D.. On the dynamics of rational maps. Ann. Sci. École Norm. Sup. (4) 16(2) (1983), 193–217.CrossRefGoogle Scholar
[38]Munkres, J. R.. Topology: A First Course. Prentice Hall, Englewood Cliffs, NJ, 1975.Google Scholar
[39]Robertson, J. W.. Dynamical objects for cohomologically expanding maps. Preprint.Google Scholar
[40]Robertson, J. W.. Complex dynamics in higher dimensions. Doctoral Dissertation, University of Michigan, 2000.Google Scholar
[41]Sibony, N.. Dynamique des applications rationnelles de . Dynamique et Géométrie Complexes (Lyon, 1997) (Panor. Synthèses, 8). Soc. Math. France, Paris, 1999, pp. ix–x, xi–xii, 97–185.Google Scholar
[42]Spanier, E. H.. Algebraic Topology. McGraw-Hill, New York, 1966.Google Scholar
[43]Sullivan, D.. Quasiconformal homeomorphisms and dynamics. I. Solution of the Fatou–Julia problem on wandering domains. Ann. of Math. (2) 122(3) (1985), 401–418.CrossRefGoogle Scholar
[44]Ueda, T.. Fatou sets in complex dynamics in projective spaces. J. Math. Soc. Japan 46 (1994), 545–555.CrossRefGoogle Scholar
[45]Ueda, T.. Complex dynamics on and Kobayashi metric. Complex Dynamical Systems and Related Areas (Kyoto, 1996) (Surikaisekikenkyusho Kokyuroku, 988). 1997, pp. 188–191.Google Scholar
[46]Ueda, T.. Critical orbits of holomorphic maps on projective spaces. J. Geom. Anal. 8(2) (1998), 319–334.Google Scholar