Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T15:06:24.777Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic spectral gap and Weyl law for Ruelle resonances of open partially expanding maps

Published online by Cambridge University Press:  07 October 2015

JEAN FRANCOIS ARNOLDI ,
FRÉDÉRIC FAURE  and
TOBIAS WEICH
JEAN FRANCOIS ARNOLDI
Affiliation:
Centre for Biodiversity Theory and Modelling, Station d’Ecologie Expérimentale du CRNRS, 09200 Moulis, France email [email protected]
FRÉDÉRIC FAURE
Affiliation:
Institut Fourier, UMR 5582, 100 rue des Maths, BP74 38402 St Martin d’Hères, France email [email protected]
TOBIAS WEICH
Affiliation:
Fachbereich Mathematik, Philipps-Universität Marburg, a Hans-Meerwein-Straße, 35032 Marburg, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a simple model of an open partially expanding map. Its trapped set 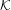${\mathcal{K}}$ in phase space is a fractal set. We first show that there is a well-defined discrete spectrum of Ruelle resonances which describes the asymptotic of correlation functions for large time and which is parametrized by the Fourier component $\unicode[STIX]{x1D708}$ in the neutral direction of the dynamics. We introduce a specific hypothesis on the dynamics that we call ‘minimal captivity’. This hypothesis is stable under perturbations and means that the dynamics is univalued in a neighborhood of 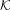${\mathcal{K}}$ . Under this hypothesis we show the existence of an asymptotic spectral gap and a fractal Weyl law for the upper bound of density of Ruelle resonances in the semiclassical limit 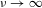$\unicode[STIX]{x1D708}\rightarrow \infty$ . Some numerical computations with the truncated Gauss map and Bowen–Series maps illustrate these results.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 1 , February 2017 , pp. 1 - 58
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artin, E.. Ein mechanisches system mit quasiergodischen bahnen. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, Vol. 3. Springer, Berlin, 1924, pp. 170–175.Google Scholar
Baladi, V. and Tsujii, M.. Dynamical determinants and spectrum for hyperbolic diffeomorphisms. Probabilistic and Geometric Structures in Dynamics (Contemporary Mathematics) . Eds. Burns, K., Dolgopyat, D. and Pesin, Ya.. American Mathematical Society, Providence, RI, 2006, Volume in honour of M. Brin’s 60th birthday. Preprint, 2006, arXiv:0606434.Google Scholar
Baladi, V. and Tsujii, M.. Anisotropic Hölder and Sobolev spaces for hyperbolic diffeomorphisms. Ann. Inst. Fourier 57 (2007), 127–154.Google Scholar
Baladi, V. and Tsujii, M.. Dynamical determinants and spectrum for hyperbolic diffeomorphisms. Geometric and Probabilistic Structures in Dynamics (Contemporary Mathematics, 469) . American Mathematical Society, Providence, RI, 2008, pp. 29–68.Google Scholar
Barkhofen, S., Weich, T., Potzuweit, A., Stöckmann, H.-J., Kuhl, U. and Zworski, M.. Experimental observation of the spectral gap in microwave n-disk systems. Phys. Rev. Lett. 110(16) (2013), 164102.Google Scholar
Blank, M., Keller, G. and Liverani, C.. Ruelle–Perron–Frobenius spectrum for Anosov maps. Nonlinearity 15 (2002), 1905–1973.Google Scholar
Borthwick, D.. Spectral Theory of Infinite-Area Hyperbolic Surfaces. Birkhäuser, Basel, 2007.Google Scholar
Borthwick, D.. Distribution of resonances for hyperbolic surfaces. Experiment. Math. 23 (2014), 25–45.Google Scholar
Borthwick, D., Judge, C. and Perry, P. A.. Selberg’s zeta function and the spectral geometry of geometrically finite hyperbolic surfaces. Comment. Math. Helv. 80(3) (2005), 483–515.Google Scholar
Bowen, R. and Series, C.. Markov maps associated with Fuchsian groups. Publ. Math. Inst. Hautes Études Sci. 50(1) (1979), 153–170.Google Scholar
Brin, M. and Stuck, G.. Introduction to Dynamical Systems. Cambridge University Press, Cambridge, 2002.Google Scholar
Córdoba, A. and Fefferman, C.. Wave packets and Fourier integral operators. Comm. Partial Differential Equations 3(11) (1978), 979–1005.Google Scholar
Dal’Bo, F.. Trajectoires Géodésiques et Horocycliques. EDP Sciences, Les Ulis, France, 2012.Google Scholar
Datchev, K. and Dyatlov, S.. Fractal Weyl laws for asymptotically hyperbolic manifolds. Geom. Funct. Anal. 23(4) (2013), 1145–1206.Google Scholar
Dimassi, M. and Sjöstrand, J.. Spectral Asymptotics in the Semi-Classical Limit (London Mathematical Society Lecture Notes, 268) . Cambridge University Press, Cambridge, 1999.Google Scholar
Dolgopyat, D.. On decay of correlations in Anosov flows. Ann. of Math. (2) 147(2) (1998), 357–390.Google Scholar
Dolgopyat, D.. On mixing properties of compact group extensions of hyperbolic systems. Israel J. Math. 130 (2002), 157–205.Google Scholar
Ermann, L. and Shepelyansky, D.. Ulam method and fractal Weyl law for Perron-Frobenius operators. Eur. Phys. J. B 75(3) (2010), 299–304.Google Scholar
Falconer, K.. Techniques in Fractal Geometry. John Wiley & Sons Ltd., Chichester, 1997.Google Scholar
Falconer, K. J.. Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons Inc, New York, 2003.CrossRefGoogle Scholar
Faure, F.. Semiclassical origin of the spectral gap for transfer operators of a partially expanding map. Nonlinearity 24 (2011), 1473–1498.Google Scholar
Faure, F. and Roy, N.. Ruelle-Pollicott resonances for real analytic hyperbolic map. Nonlinearity 19 (2006), 1233–1252.Google Scholar
Faure, F., Roy, N. and Sjöstrand, J.. A semiclassical approach for Anosov diffeomorphisms and Ruelle resonances. Open Math. J. 1 (2008), 35–81.Google Scholar
Faure, F. and Sjöstrand, J.. Upper bound on the density of Ruelle resonances for Anosov flows. A semiclassical approach. Comm. Math. Phys. 308(2) (2011), 325–364.CrossRefGoogle Scholar
Faure, F. and Tsujii, M.. Prequantum transfer operator for symplectic Anosov diffeomorphism. Asterisque (2012) submitted.Google Scholar
Faure, F. and Tsujii, M.. Band structure of the Ruelle spectrum of contact Anosov flows. C. R. Math. Acad. Sci. Paris 351 (2013), 385–391.CrossRefGoogle Scholar
Gohberg, I., Goldberg, S. and Krupnik, N.. Traces and Determinants of Linear Operators. Birkhäuser, Basel, 2000.Google Scholar
Gouëzel, S. and Liverani, C.. Banach spaces adapted to Anosov systems. Ergod. Th. & Dynam. Sys. 26 (2005), 189–217.CrossRefGoogle Scholar
Grigis, A. and Sjöstrand, J.. Microlocal Analysis for Differential Operators: An Introduction (London Mathematical Society Lecture Note Series, 196) . Cambridge University Press, Cambridge, 1994.Google Scholar
Guillope, L., Lin, K. and Zworski, M.. The Selberg zeta function for convex co-compact Schottky groups. Comm. Math. Phys. 245(1) (2004), 149–176.Google Scholar
Hörmander, L.. The Analysis of Linear Partial Differential Operators III, Vol. 257. Springer, Berlin, 1983.Google Scholar
Hormander, L.. The Analysis of the Linear Partial Differential Operators I: Distribution Theory and Fourier Analysis (Classics in Mathematics) . Springer, Berlin, 2003.Google Scholar
Jenkinson, O. and Pollicott, M.. Calculating Hausdorff dimension of Julia sets and Kleinian limit sets. Amer. J. Math. 124(3) (2002), 495–545.CrossRefGoogle Scholar
Kitaev, A. Yu.. Fredholm determinants for hyperbolic diffeomorphisms of finite smoothness. Nonlinearity 12(1) (1999), 141–179.CrossRefGoogle Scholar
Körber, M., Michler, M., Bäcker, A. and Ketzmerick, R.. Hierarchical fractal Weyl laws for chaotic resonance states in open mixed systems. Phys. Rev. Lett. 111(11) (2013), 114102.Google Scholar
Lu, W., Sridhar, S. and Zworski, M.. Fractal Weyl laws for chaotic open systems. Phys. Rev. Lett. 91(15) (2003), 154101.Google Scholar
Martinez, A.. An Introduction to Semiclassical and Microlocal Analysis (Universitext) . Springer, New York, 2002.Google Scholar
Mattila, P.. Geometry of Sets and Measures in Euclidean Spaces: Fractals and Rectifiability, Vol. 44. Cambridge University Press, Cambridge, 1999.Google Scholar
Mayer, D. H.. On the thermodynamic formalism for the gauss map. Comm. Math. Phys. 130(2) (1990), 311–333.Google Scholar
Naud, F.. Expanding maps on cantor sets and analytic continuation of zeta functions. Ann. Sci. Ecole Norm. Sup. 38 (2005), 116–153.Google Scholar
Nonnenmacher, S.. Spectral problems in open quantum chaos. Nonlinearity 24(12) (2011), R123.CrossRefGoogle Scholar
Nonnenmacher, S., Sjöstrand, J. and Zworski, M.. Fractal Weyl law for open quantum chaotic maps. Ann. of Math. (2) 179(1) (2014), 179–251.CrossRefGoogle Scholar
Patterson, S. J. and Perry, P. A.. The divisor of Selberg’s zeta function for Kleinian groups. Duke Math. J. 106(2) (2001), 321–390.Google Scholar
Pesin, Y.. Lectures on Partial Hyperbolicity and Stable Ergodicity. European Mathematical Society, Zurich, 2004.Google Scholar
Pollicott, M. and Rocha, A.C.. A remarkable formula for the determinant of the Laplacian. Invent. Math. 130(2) (1997), 399–414.Google Scholar
Potzuweit, A., Weich, T., Barkhofen, S., Kuhl, U., Stöckmann, H.-J. and Zworski, M.. Weyl asymptotics: from closed to open systems. Phys. Rev. E 86(6) (2012), 066205.Google Scholar
Reed, M. and Simon, B.. Mathematical Methods in Physics, vol. I: Functional Analysis. Academic Press, New York, 1972.Google Scholar
Ruelle, D.. Zeta-functions for expanding maps and Anosov flows. Invent. Math. 34(3) (1976), 231–242.Google Scholar
Ruelle, D. The thermodynamic formalism for expanding maps. Comm. Math. Phys. 125(2) (1989), 239–262.Google Scholar
Schomerus, H. and Tworzydło, J.. Quantum-to-classical crossover of quasibound states in open quantum systems. Phys. Rev. Lett. 93(15) (2004), 154102.Google Scholar
Sjöstrand, J.. Geometric bounds on the density of resonances for semiclassical problems. Duke Math. J. 60(1) (1990), 1–57.Google Scholar
Taylor, M.. Partial Differential Equations, Vol. I. Springer, Berlin, 1996.Google Scholar
Taylor, M.. Partial Differential Equations, Vol. II. Springer, Berlin, 1996.Google Scholar
Tsujii, M.. Decay of correlations in suspension semi-flows of angle-multiplying maps. Ergod. Th. & Dynam. Sys. 28 (2008), 291–317.Google Scholar
Wolfgang, F.. Über die Existenz des zweiten Eigenwertes der G N -Operatoren bei grossem N . Anz. Österreich. Akad. Wiss. Math.-Natur. Kl. 1991(7) (1991), 97–101.Google Scholar
Zworski, M.. Dimension of the limit set and the density of resonances for convex co-compact hyperbolic surfaces. Invent. Math. 136(2) (1999), 353–409.Google Scholar
Zworski, M.. Semiclassical Analysis (Graduate Studies in Mathematics Series) . American Mathematical Society, Providence, RI, 2012.Google Scholar