Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-01T00:26:32.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Area-preserving diffeomorphisms of the torus whose rotation sets have non-empty interior

Published online by Cambridge University Press:  13 August 2013

SALVADOR ADDAS-ZANATA
SALVADOR ADDAS-ZANATA*
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Rua do Matão 1010, Cidade Universitária, 05508-090 São Paulo, SP, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider 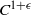${C}^{1+ \epsilon } $ area-preserving diffeomorphisms of the torus 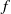$f$, either homotopic to the identity or to Dehn twists. We suppose that 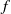$f$ has a lift 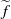$\widetilde {f} $ to the plane such that its rotation set has interior and prove, among other things, that if zero is an interior point of the rotation set, then there exists a hyperbolic 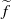$\widetilde {f} $-periodic point 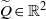$\widetilde {Q} \in { \mathbb{R} }^{2} $ such that 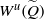${W}^{u} (\widetilde {Q} )$ intersects 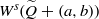${W}^{s} (\widetilde {Q} + (a, b))$ for all integers 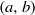$(a, b)$, which implies that 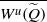$ \overline{{W}^{u} (\widetilde {Q} )} $ is invariant under integer translations. Moreover, 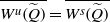$ \overline{{W}^{u} (\widetilde {Q} )} = \overline{{W}^{s} (\widetilde {Q} )} $ and 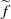$\widetilde {f} $ restricted to 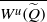$ \overline{{W}^{u} (\widetilde {Q} )} $ is invariant and topologically mixing. Each connected component of the complement of 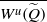$ \overline{{W}^{u} (\widetilde {Q} )} $ is a disk with diameter uniformly bounded from above. If 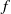$f$ is transitive, then 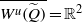$ \overline{{W}^{u} (\widetilde {Q} )} = { \mathbb{R} }^{2} $ and 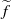$\widetilde {f} $ is topologically mixing in the whole plane.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 1 , February 2015 , pp. 1 - 33
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Addas-Zanata, S.. On the existence of a new type of periodic and quasi-periodic orbits for twist maps of the torus. Nonlinearity 15 (2002), 1399–1416.Google Scholar
Addas-Zanata, S.. A note on a standard family of twist maps. Qual. Theory Dyn. Syst. 5 (2004), 1–9.Google Scholar
Addas-Zanata, S.. Some extensions of the Poincaré–Birkhoff theorem to the cylinder and a remark on mappings of the torus homotopic to Dehn twists. Nonlinearity 18 (2005), 2243–2260.Google Scholar
Addas-Zanata, S. and Tal, F.. Homeomorphisms of the annulus with a transitive lift. Math. Z. 267 (2011), 971–980.Google Scholar
Addas-Zanata, S., Garcia, B. and Tal, F.. On the dynamics of homeomorphisms of the torus homotopic to Dehn twists. Ergod. Th. & Dynam. Sys., to appear. doi: 10.1017/etds.2012.156.Google Scholar
Boyland, P.. Isotopy stability of dynamics on surfaces. Contemp. Math. 246 (1999), 17–45.Google Scholar
Brown, M.. Homeomorphisms of two-manifolds. Houston J. Math. 11 (1985), 455–469.Google Scholar
de Carvalho, A. and Paternain, M.. Monotone quotients of surface diffeomorphisms. Math. Res. Lett. 10 (2003), 603–619.CrossRefGoogle Scholar
Doeff, E.. Rotation measures for homeomorphisms of the torus homotopic to a Dehn twist. Ergod. Th. & Dynam. Sys. 17 (1997), 1–17.Google Scholar
Duarte, P.. Plenty of elliptic islands for the standard family of area preserving maps. Ann. Inst. H. Poincaré Anal. Non Linéaire 11 (1994), 359–409.Google Scholar
Epstein, D.. Curves on 2-manifolds and isotopies. Acta Math. 115 (1966), 83–107.Google Scholar
Fathi, A., Laudenbach, F. and Poenaru, V.. Travaux de Thurston sur les surfaces. Astérisque. 66–67 (1979).Google Scholar
Franks, J.. Realizing rotation vectors for torus homeomorphisms. Trans. Amer. Math. Soc. 311 (1989), 107–115.Google Scholar
Franks, J. and Le Calvez, P.. Regions of instability for non-twist maps. Ergod. Th. & Dynam. Sys. 23 (2003), 111–141.CrossRefGoogle Scholar
Guelman, N., Koropecki, A. and Tal, F.. (2013), Rotation sets with non-empty interior and transitivity in the universal covering. Ergod. Th. & Dynam. Sys., to appear.CrossRefGoogle Scholar
Handel, M.. Global shadowing of pseudo-Anosov homeomorphisms. Ergod. Th. & Dynam. Sys. 5 (1985), 373–377.Google Scholar
Handel, M.. The rotation set of a homeomorphism of the annulus is closed. Comm. Math. Phys. 127 (1990), 339–349.Google Scholar
Handel, M. and Thurston, W.. New proofs of some results of Nielsen. Adv. Math. 56 (1985), 173–191.Google Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Khinchin, A.. Continued Fractions. Dover edition, New York, 1997.Google Scholar
Koropecki, A. and Tal, F.. Strictly toral dynamics. Invent. Math., to appear.Google Scholar
Kwapisz, J.. Every convex polygon with rational vertices is a rotation set. Ergod. Th. & Dynam. Sys. 12 (1992), 333–339.CrossRefGoogle Scholar
Kwapisz, J.. A toral diffeomorphism with a nonpolygonal rotation set. Nonlinearity 8 (1995), 461–476.Google Scholar
Kwapisz, J.. Rotation sets and entropy. PhD Thesis, 1995, SUNY at Stony Brook, USA.Google Scholar
Kwapisz, J. and Swanson, R.. Asymptotic entropy, periodic orbits, and pseudo-Anosov maps. Ergod. Th. & Dynam. Sys. 18 (1998), 425–439.Google Scholar
Llibre, J. and Mackay, R.. Rotation vectors and entropy for homeomorphisms of the torus isotopic to the identity. Ergod. Th. & Dynam. Sys. 11 (1991), 115–128.Google Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets for maps of tori. J. Lond. Math. Soc. 40 (1989), 490–506.Google Scholar
Thurston, W.. On the geometry and dynamics of diffeomorphisms of surfaces. Bull. Amer. Math. Soc. 19 (1988), 417–431.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York–Berlin, 1982.Google Scholar