Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T03:04:29.511Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation of Bernoulli measures for non-uniformly hyperbolic systems

Published online by Cambridge University Press:  11 May 2018

GANG LIAO ,
WENXIANG SUN ,
EDSON VARGAS  and
SHIROU WANG
GANG LIAO
Affiliation:
School of Mathematical Sciences, Soochow University, Suzhou 215006, China email [email protected]
WENXIANG SUN
Affiliation:
School of Mathematical Sciences, Peking University, Beijing 100871, China email [email protected]
EDSON VARGAS
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Rua do Matão 1010, CEP 05508-090, São Paulo, SP, Brazil email [email protected]
SHIROU WANG
Affiliation:
Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China email [email protected] Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton T6G2G1, Alberta, Canada email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An invariant measure is called a Bernoulli measure if the corresponding dynamics is isomorphic to a Bernoulli shift. We prove that for 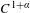$C^{1+\unicode[STIX]{x1D6FC}}$ diffeomorphisms any weak mixing hyperbolic measure could be approximated by Bernoulli measures. This also holds true for $C^{1}$ diffeomorphisms preserving a weak mixing hyperbolic measure with respect to which the Oseledets decomposition is dominated.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 1 , January 2020 , pp. 233 - 247
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdenur, F., Bonatti, C. and Crovisier, S.. Uniform hyperbolicity for C 1 -generic diffeomorphisms. Israel J. Math. 183 (2011), 1–60.10.1007/s11856-011-0041-5Google Scholar
Abdenur, F. and Crovisier, S.. Transitivity and topological mixing for C 1 -diffeomorphisms. Essays in Mathematics and its Applications. Springer, Berlin, Heidelberg, 2012, pp. 1–16.Google Scholar
Arbieto, A., Catalan, T. and Santiago, B.. Mixing-like properties for some generic and robust dynamics. Nonlinearity 28(11) (2015), 4103–4115.10.1088/0951-7715/28/11/4103Google Scholar
Bonatti, C., Crovisier, S. and Shinohara, K.. The C 1+𝛼 hypothesis in Pesin theory revisited. J. Mod. Dyn. 7(4) (2013), 605–618.Google Scholar
Bowen, R.. Markov partitions for Axiom A diffeomorphisms. Amer. J. Math. 92 (1970), 725–747.10.2307/2373370Google Scholar
Gan, S.. A generalized shadowing lemma. Discrete Contin. Dyn. Syst. 8(3) (2002), 627–632.10.3934/dcds.2002.8.627Google Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.10.1007/BF02684777Google Scholar
Katok, A. and Mendaza, L.. Dynamical systems with nonuniformly hyperbolic behavior, supplement to the book by A. Katok and B. Hasselblatt. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, New York, 1995.10.1017/CBO9780511809187Google Scholar
Liao, G., Sun, W. and Wang, S.. Upper semi-continuity of entropy map for nonuniformly hyperbolic systems. Nonlinearity 28 (2015), 2977–2992.10.1088/0951-7715/28/8/2977Google Scholar
Liao, S.. An existence theorem for periodic orbits. Acta Sci. Natur. Univ. Pekinensis 1 (1979), 1–20.Google Scholar
Moser, J., Phillips, E. and Varadhan, S.. Ergodic Theory: A Seminar. Courant Institute of Mathematical Sciences, New York University, New York, 1975.Google Scholar
Ornstein, D. S.. Ergodic Theory, Randomness and Dynamical Systems (Yale Mathematical Monographs, 5) . Yale University, New Haven, CT, 1974.Google Scholar
Pesin, Ja. B.. Families of invariant manifolds corresponding to nonzero characteristic exponents. Math. USSR-Izv. 10(6) (1976), 1261–1305.10.1070/IM1976v010n06ABEH001835Google Scholar
Pesin, Ja. B.. Characteristic Lyapunov exponents and smooth ergodic theory. Russian Math. Surveys 32(4) (1977), 55–114.10.1070/RM1977v032n04ABEH001639Google Scholar
Pugh, C. C.. The C 1+𝛼 hypothesis in Pesin theory. Publ. Math. Inst. Hautes Études Sci. 59 (1984), 143–161.10.1007/BF02698771Google Scholar
Robinson, C.. Dynamical Systems: Stability, Symbolic Dynamics, and Chaos. CRC Press, Boca Raton, CA, 1995.Google Scholar
Shields, P. C.. The Theory of Bernoulli Shifts. University of Chicago Press, Chicago, IL, 1973.Google Scholar
Sigmund, K.. On mixing measures for Axiom A diffeomorphisms. Proc. Amer. Math. Soc. 36(2) (1972), 497–504.10.1090/S0002-9939-1972-0309155-3Google Scholar
Sun, W. and Tian, X.. Dominated splittings and Pesin’s entropy formula. Discrete Contin. Dyn. Syst. 32 (2012), 1421–1434.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.10.1007/978-1-4612-5775-2Google Scholar