Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T00:54:36.606Z Has data issue: false hasContentIssue false
  • English
  • Français

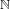Approximate transitivity of the ergodic action of the group of finite permutations of $\mathbb{N}$ on $\{0,1\}^{\mathbb{N}}$

Published online by Cambridge University Press:  13 March 2018

B. MITCHELL BAKER ,
THIERRY GIORDANO  and
RADU B. MUNTEANU
B. MITCHELL BAKER
Affiliation:
Mathematics Department, U.S. Naval Academy, Chauvenet Hall, 572C Holloway Road, Annapolis, MD 21402-5002, USA email [email protected]
THIERRY GIORDANO
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, Ottawa, Canada K1N 6N5 email [email protected]
RADU B. MUNTEANU
Affiliation:
Department of Mathematics, University of Bucharest, 14 Academiei Street, 010014, Bucharest, Romania Simion Stoilow Institute of Mathematics of the Romanian Academy, 21 Calea Grivitei Street, 010702, Bucharest, Romania email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we show that the natural action of the symmetric group acting on the product space 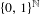$\{0,1\}^{\mathbb{N}}$ endowed with a Bernoulli measure is approximately transitive. We also extend the result to a larger class of probability measures.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 11 , November 2019 , pp. 2881 - 2895
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

El Abdalaoui, E. H. and Lemanczyk, M.. Approximately transitive dynamical systems and simple spectrum. Arch. Math. 97 (2011), 187–197.Google Scholar
Adams, S., Elliott, G. A. and Giordano, T.. Amenable actions of groups. Trans. Amer. Math. Soc. 344(2) (1994), 803–822.Google Scholar
Aldous, D. and Pitman, J.. On the zero-one law for exchangeable events. Ann. Probab. 7(1) (1979), 704–723.10.1214/aop/1176994992Google Scholar
Baker, B. M.. Free states of the gauge invariant canonical anticommutation relations. Trans. Amer. Math. Soc. 237 (1978), 35–61.10.1090/S0002-9947-1978-0479361-6Google Scholar
Baker, B. M. and Powers, R. T.. Product states on the gauge invariant and rotationally invariant CAR algebras. J. Operator Theory 10 (1983), 365–393.Google Scholar
Connes, A.. Une classification des facteurs de type III. Ann. Sci. Éc. Norm. Supér. (4) 6 (1973), 133–252.Google Scholar
Connes, A. and Woods, E. J.. Approximately transitive flows and ITPFI factors. Ergod. Th. & Dynam. Sys. 5 (1985), 203–236.Google Scholar
Connes, A. and Woods, E. J.. Hyperfinite von Neumann algebras and Poisson boundaries of time dependent random walks. Pacific J. Math. 137 (1989), 225–243.Google Scholar
Dooley, A. H. and Quas, A.. Approximate transitivity for zero-entropy systems. Ergod. Th. & Dynam. Sys. 25 (2005), 443–453.Google Scholar
Elliott, G. A. and Giordano, T.. Amenable actions of discrete groups. Ergod. Th. & Dynam. Sys. 13 (1993), 289–318.Google Scholar
Elliott, G. A. and Giordano, T.. Every approximately transitive amenable action of a locally compact group is a Poisson boundary. C. R. Acad. Sci. Canada 21 (1999), 9–15.Google Scholar
Giordano, T. and Handelman, D.. Matrix-valued random walks and variations on property AT. Munster J. Math. 1 (2008), 15–72.Google Scholar
Giordano, T. and Munteanu, R. B.. Von Neumann algebras arising as fixed point algebras under xerox type actions. J. Operator Theory 72 (2014), 343–369.Google Scholar
Hamachi, T. and Osikawa, M.. Ergodic groups of automorphisms and Krieger’s theorem. Sem. Math. Sci. Keio University 3 (1981), 1–113.Google Scholar
Hewitt, E. and Stromberg, K.. Real and Abstract Analysis. Springer, New York, 1965.Google Scholar
Krieger, W.. On ergodic flows and isomorphisms of factors. Math. Ann. 223 (1976), 19–70.Google Scholar
Sutherland, C. E.. Notes on Orbit Equivalence: Krieger’s Theorem (Lecture Notes Series, 23) . Mathematical Institute, University of Oslo, Oslo, 1976.Google Scholar
Stratila, S. and Voiculescu, D. V.. On a class of KMS states for the unitary group U (∞). Math. Ann. 235 (1978), 87–110.10.1007/BF01421594Google Scholar
Takesaki, M.. Duality for crossed products and the structure of von Neumann algebras of type III. Acta Math. 131 (1973), 249–310.Google Scholar