No CrossRef data available.
Published online by Cambridge University Press: 04 May 2017
We consider the dynamical properties of 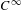 $C^{\infty }$-variations of the flow on an aperiodic Kuperberg plug
$C^{\infty }$-variations of the flow on an aperiodic Kuperberg plug  $\mathbb{K}$. Our main result is that there exists a smooth one-parameter family of plugs
$\mathbb{K}$. Our main result is that there exists a smooth one-parameter family of plugs 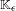 $\mathbb{K}_{\unicode[STIX]{x1D716}}$ for
$\mathbb{K}_{\unicode[STIX]{x1D716}}$ for 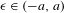 $\unicode[STIX]{x1D716}\in (-a,a)$ and
$\unicode[STIX]{x1D716}\in (-a,a)$ and 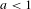 $a<1$, such that: (1) the plug
$a<1$, such that: (1) the plug 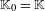 $\mathbb{K}_{0}=\mathbb{K}$ is a generic Kuperberg plug; (2) for
$\mathbb{K}_{0}=\mathbb{K}$ is a generic Kuperberg plug; (2) for 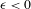 $\unicode[STIX]{x1D716}<0$, the flow in the plug
$\unicode[STIX]{x1D716}<0$, the flow in the plug 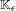 $\mathbb{K}_{\unicode[STIX]{x1D716}}$ has two periodic orbits that bound an invariant cylinder, all other orbits of the flow are wandering, and the flow has topological entropy zero; (3) for
$\mathbb{K}_{\unicode[STIX]{x1D716}}$ has two periodic orbits that bound an invariant cylinder, all other orbits of the flow are wandering, and the flow has topological entropy zero; (3) for 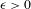 $\unicode[STIX]{x1D716}>0$, the flow in the plug
$\unicode[STIX]{x1D716}>0$, the flow in the plug 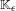 $\mathbb{K}_{\unicode[STIX]{x1D716}}$ has positive topological entropy, and an abundance of periodic orbits.
$\mathbb{K}_{\unicode[STIX]{x1D716}}$ has positive topological entropy, and an abundance of periodic orbits.