Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:35:12.128Z Has data issue: false hasContentIssue false
  • English
  • Français

An obstruction to the existence of certain dynamics in surface diffeomorphisms

Published online by Cambridge University Press:  19 September 2008

Paul Blanchard  and
John Franks
Paul Blanchard
Affiliation:
Boston University, Boston, MA 02215
John Franks
Affiliation:
Northwestern University, Evanston, Illinois, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be a two-dimensional, compact manifold and g:Μ→ΜM be a diffeomorphism with a hyperbolic chain recurrent set. We find restrictions on the reduced zeta function p(t) of anyzero-dimensional basic set of g. If deg (p(t)) is odd, then p(1) = 0 (in 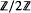). Since there are infinitely many subshifts of finite type whose reduced zeta functions do not satisfy these restrictions, there are infinitely many subshifts which cannot be basic sets for any diffeomorphism of any surface.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 1 , Issue 3 , September 1981 , pp. 255 - 260
Copyright
Copyright © Cambridge University Press 1981

References

REFERENCES

[1]Artin, M. & Mazur, B.. On periodic points. Ann. Math. 81 (1965), 82–99.CrossRefGoogle Scholar
[2]Bowen, R.. Entropy versus homology for certain diffeomorphisms. Topology 13 (1974), 61–67.CrossRefGoogle Scholar
[3]Bowen, R. & Lanford, O.. Zeta functions of restrictions of the shifttransformation. Proceedings of the Symposia in Pure Mathematics. Amer. Math. Soc. 14 (1970), 43–49.Google Scholar
[4]Franke, J. & Selgrade, J.. Hyperbolicity and chain recurrence. J. Diff. Equations 26 (1977), 27–36.CrossRefGoogle Scholar
[5]Franks, J.. A reduced zeta function for diffeomorphisms. Amer. J. Math. 100 (1978), 217–243.CrossRefGoogle Scholar
[6]Franks, J.. Homology and dynamical systems. The Conference Board of the Mathematical Sciences, Regional Conference Series in Mathematics. Amer. Math. Soc. (to appear).Google Scholar
[7]Guckenheimer, J.. Axiom A and no cycles imply ζf(t) rational. Bull. Amer. Math. Soc. 76 (1970), 592–594.CrossRefGoogle Scholar
[8]Manning, A.. Axiom A diffeomorphisms have rational zeta functions. Bull. London Math. Soc. 3 (1971), 215–220.CrossRefGoogle Scholar
[9]Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.CrossRefGoogle Scholar
[10]Smale, S.. The Ω-stability theorem. Proceedings of the Symposia in PureMathematics. Amer. Math. Soc. 14 (1970), 289–297.Google Scholar
[11]Williams, R. F.. Classification of subshifts of finite type. Ann. Math. 98 (1973), 120–153.CrossRefGoogle Scholar
[12]Williams, R. F.. The zeta function of an attractor. Proceedings of the Conference on the Topology of Manifolds (Michigan State, 1967) (ed. Hocking, J. G.), pp. 155–161. Prindle, Weber and Schmidt, 1968.Google Scholar
[13]Wilson, F. W. Jr. Smoothing derivatives of functions and applications. Trans. Amer. Math. Soc. 139 (1969), 413–428.CrossRefGoogle Scholar