Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:41:48.812Z Has data issue: false hasContentIssue false
  • English
  • Français

An explosion point for the set of endpoints of the Julia set of λ exp (z)

Published online by Cambridge University Press:  19 September 2008

John C. Mayer
John C. Mayer
Affiliation:
Department of Mathematics, University of Alabama at Birmingham, Birmingham, AL 35294, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

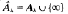The Julia set Jλ of the complex exponential function Eλ: z → λez for a real parameter λ(0 < λ < 1/e) is known to be a Cantor bouquet of rays extending from the set Aλ of endpoints of Jλ to ∞. Since Aλ contains all the repelling periodic points of Eλ, it follows that Jλ = Cl (Aλ). We show that Aλ is a totally disconnected subspace of the complex plane ℂ, but if the point at ∞ is added, then is a connected subspace of the Riemann sphere 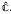. As a corollary, Aλ has topological dimension 1. Thus, ∞ is an explosion point in the topological sense for Âλ. It is remarkable that a space with an explosion point occurs ‘naturally’ in this way.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 10 , Issue 1 , March 1990 , pp. 177 - 183
Copyright
Copyright © Cambridge University Press 1990

References

REFERENCES

[B]Baker, I. N.. Wandering domains in the iteration of entire functions. Proc. London Math. Soc. 49 (1984), 563–576.Google Scholar
[B1]Blanchard, P.. Complex analytic dynamics on the Riemann sphere. Bull. Amer. Math. Soc. 11 (1984), 85–141.Google Scholar
[Br]Brechner, B. L.. On stable homeomorphisms and imbeddings of the pseudo arc. Illinois J. Math. 22 (1978), 630–661.CrossRefGoogle Scholar
[BO]Bula, W. T. & Oversteegen, L. G.. A characterization of smooth Cantor bouquets. Proc. Amer. Math. Soc. to appear.Google Scholar
[C]Caratheodory, C.. Über die Begrenzung einfach zusammenhangender Gebiete. Math. Ann. 73 (1913), 323–370.CrossRefGoogle Scholar
[CL]Collingwood, E. F. & Lohwater, A. J.. The Theory of Cluster Sets. Cambridge Tracts in Mathematics and Mathematical Physics 56, Cambridge University Press: Cambridge, 1966.Google Scholar
[D1]Devaney, R. L.. ez dynamics and bifurcations. Preprint.CrossRefGoogle Scholar
[D2]Devaney, R. L.. The structural instability of exp (z). Proc. Amer. Math. Soc. 94 (1985), 545–548.Google Scholar
[D3]Devaney, R. L.. An Introduction to Chaotic Dynamical Systems. Benjamin/Cummings: Menlo Park, CA, 1986.Google Scholar
[DG]Devaney, R. L. & Goldberg, L. R.. Uniformization of attracting basins. Duke Math. J. 55 (1987) 253–266.CrossRefGoogle Scholar
[DGH]Devaney, R. L., Goldberg, L. R. & Hubbard, J. H.. A dynamical approximation of the exponential by polynomials. To appear.Google Scholar
[DK]Devaney, R. L. & Krych, M.. Dynamics of exp (z). Ergod. Th. & Dynam. Sys. 4 (1984), 35–52.CrossRefGoogle Scholar
[DT]Devaney, R. L. & Tangerman, F.. Dynamics of entire functions near the essential singularity. Ergod. Th. & Dynam. Syst. 6 (1986), 498–503.CrossRefGoogle Scholar
[F]Fatou, P.. Sur l'itération des fonctions transcendantes entières. Acta Math. 47 (1926), 337–370.CrossRefGoogle Scholar
[GK]Goldberg, L. R. & Keen, L.. A finiteness theorem for a dynamical class of entire functions. Ergod. Th. & Dynam. Sys. 6 (1986), 183–192.Google Scholar
[HW]Hurewicz, W. & Wallman, H.. Dimension Theory. Princeton University Press: Princeton, NJ, 1974.Google Scholar
[J]Julia, G.. Memoire sur l'itération des fonctions rationelles. J. Math. Pures Appl. 8 (1918), 47–225.Google Scholar
[Ke]Keesling, J. E.. Hausdorff dimension. Topology Proc. 11 (1986), 349–383.Google Scholar
[Ku]Kuratowski, K.. Topology, Volumes I and II. Academic Press: New York, 1968.Google Scholar
[L]Lelek, A.. On plane dendroids and their endpoints in the classical sense. Fund. Math. 49 (1961), 301–319.Google Scholar
[M]Mather, J. N.. Topological proofs of some purely topological consequences of Caratheodory's theory of prime ends. Selected Studies, Rassias, Th. M. & Rassias, G. M., eds., pp. 225–255, North-Holland: Amsterdam, 1982.Google Scholar
[Mc]McMullen, C.. Area and Hausdorff dimension of Julia sets of entire functions. Trans. Amer. Math. Soc. 300 (1987), 329–342.Google Scholar
[Mi]Misiurewicz, M.. On iterates of e z, Ergod. Th. & Dynam. Sys. 1 (1981), 103–106.Google Scholar
[P]Piranian, G.. The boundary of a simply connected domain, Bull. Amer. Math. Soc. 64 (1958), 45–55.Google Scholar
[UY]Ursell, H. D. & Young, L. C.. Remarks on the theory of prime ends. Mem. Amer. Math. Soc. 3 (1951).Google Scholar