Hostname: page-component-f554764f5-nt87m Total loading time: 0 Render date: 2025-04-11T09:12:16.551Z Has data issue: false hasContentIssue false
  • English
  • Français

An autocorrelation and a discrete spectrum for dynamical systems on metric spaces

Part of: Measure-theoretic ergodic theory Ergodic theory

Published online by Cambridge University Press:  27 November 2019

DANIEL LENZ
DANIEL LENZ*
Affiliation:
Mathematisches Institut, Friedrich Schiller Universität Jena, D-03477Jena, Germany email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study dynamical systems 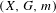$(X,G,m)$ with a compact metric space 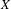$X$, a locally compact, $\unicode[STIX]{x1D70E}$-compact, abelian group 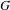$G$ and an invariant Borel probability measure $m$ on 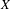$X$. We show that such a system has a discrete spectrum if and only if a certain space average over the metric is a Bohr almost periodic function. In this way, this average over the metric plays, for general dynamical systems, a similar role to that of the autocorrelation measure in the study of aperiodic order for special dynamical systems based on point sets.

Keywords

classical ergodic theorygroup actionstopological dynamics

MSC classification

Primary: 28D05: Measure-preserving transformations
Secondary: 37A35: Entropy and other invariants, isomorphism, classification
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 3 , March 2021 , pp. 906 - 922
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Cambridge University Press, 2019

References

Baake, M. and Grimm, U.. Aperiodic Order. Vol. 1: A Mathematical Invitation. Cambridge University Press, Cambridge, 2013.CrossRefGoogle Scholar
Baake, M. and Lenz, D.. Dynamical systems on translation bounded measures: pure point dynamical and diffraction spectra. Ergod. Th. & Dynam. Sys. 24 (2004), 1867–1893.CrossRefGoogle Scholar
Baake, M. and Lenz, D.. Spectral notions of aperiodic order. Discrete Contin. Dyn. Syst. Ser. S 10 (2017), 161–190.Google Scholar
Baake, M. and Moody, R. V.. Weighted Dirac combs with pure point diffraction. J. Reine Angew. Math. (Crelle) 573 (2004), 61–94.Google Scholar
Berg, C. and Forst, G.. Potential Theory on Locally Compact Abelian Groups. Springer, Berlin, 1975.CrossRefGoogle Scholar
Dworkin, S.. Spectral theory and X-ray diffraction. J. Math. Phys. 34 (1993), 2965–2967.CrossRefGoogle Scholar
Folland, G. B.. A Course in Abstract Harmonic Analysis. CRC Press, Boca Raton, FL, 1995.Google Scholar
Fuhrmann, G., Gröger, M. and Jäger, T.. Amorphic complexity. Nonlinearity 29 (2016), 528–565.CrossRefGoogle Scholar
Garcia-Ramos, F.. Weak forms of topological and measure theoretical equicontinuity: relationships with discrete spectrum and sequence entropy. Ergod. Th. & Dynam. Sys. 37(4) (2017), 1211–1237.CrossRefGoogle Scholar
Garcia-Ramos, F. and Marcus, B.. Mean sensitive, mean equicontinuous and almost periodic functions for dynamical systems. Discrete Contin. Dyn. Syst. Ser. A 39(2) (2019), 729–746.CrossRefGoogle Scholar
Glasner, E. and Downarowicz, T.. Isomorphic extensions and applications. Topol. Methods Nonlinear Anal. 48(1) (2016), 321–338.Google Scholar
Gouéré, J.-B.. Quasicrystals and almost periodicity. Commun. Math. Phys. 255 (2005), 655–681.CrossRefGoogle Scholar
Kellendonk, J., Lenz, D. and Savinien, J. (Eds). Mathematics of Aperiodic Order (Progress in Mathematics, 309) . Birkhäuser, Basel, 2015.CrossRefGoogle Scholar
Lee, J.-Y., Moody, R. V. and Solomyak, B.. Pure point dynamical and diffraction spectra. Ann. Henri Poincaré 3 (2002), 1003–1018.CrossRefGoogle Scholar
Lenz, D.. Aperiodic Order via Dynamical Systems: Diffraction Theory for Sets of Finite Local Complexity (Contemporary Mathematics, 485) . Ed. Assani, I.. American Mathematical Society, Providence, RI, 2009, pp. 91–112.Google Scholar
Lenz, D.. Continuity of eigenfunctions of uniquely ergodic dynamical systems and intensity of Bragg peaks. Commun. Math. Phys. 287 (2009), 225–258.CrossRefGoogle Scholar
Lenz, D. and Moody, R. V.. Stationary processes with pure point diffraction. Ergod. Th. & Dynam. Sys. 37 (2017), 2597–2642.CrossRefGoogle Scholar
Lenz, D. and Strungaru, N.. Pure point spectrum for measure dynamical systems on locally compact Abelian groups. J. Math. Pures Appl. 92 (2009), 323–341.CrossRefGoogle Scholar
Loomis, L. H.. An Introduction to Abstract Harmonic Analysis. Van Nostrand, Princeton, NJ, 1953; reprint Dover, New York, 2011.Google Scholar
Patera, J. (Ed). Quasicrystals and Discrete Geometry (Fields Institute Monographs, 10) . American Mathematical Society, Providence, RI, 1998.CrossRefGoogle Scholar
Robinson, E. A.. The dynamical properties of Penrose tilings. Trans. Amer. Math. Soc. 348 (1996), 4447–4464.CrossRefGoogle Scholar
Schlottmann, M.. Generalised model sets and dynamical systems. Directions in Mathematical Quasicrystals (CRM Monograph Series, 13) . Eds. Baake, M. and Moody, R.V.. American Mathematical Society, Providence, RI, 2000, pp. 143–159.Google Scholar
Solomyak, B.. Spectrum of dynamical systems arising from Delone sets. Quasicrystals and Discrete Geometry (Fields Institute Monographs, 10). Ed. J. Patera. American Mathematical Society, Providence, RI, 1998, [ 20 ]. pp. 265–275.CrossRefGoogle Scholar
Solomyak, B.. Dynamics of self-similar tilings. Ergod. Th. & Dynam. Sys. 17 (1997), 695–738; Erratum: Ergod. Th. & Dynam. Sys. 19 (1999), 1685.CrossRefGoogle Scholar
Vershik, A.. Scaling entropy and automorphisms with purely point spectrum. St. Petersburg Math. J. 1 (2011), 111–135.Google Scholar