Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:30:51.859Z Has data issue: false hasContentIssue false
  • English
  • Français

An almost mixing of all orders property of algebraic dynamical systems

Published online by Cambridge University Press:  07 September 2017

L. ARENAS-CARMONA ,
D. BEREND  and
V. BERGELSON
L. ARENAS-CARMONA
Affiliation:
Department of Mathematics, University of Chile, Casilla 653, Santiago, Chile email [email protected]
D. BEREND
Affiliation:
Departments of Mathematics and Computer Science, Ben-Gurion University, Beer Sheva 84105, Israel email [email protected]
V. BERGELSON
Affiliation:
Department of Mathematics, Ohio State University, Columbus, OH 43210, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider dynamical systems, consisting of 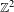$\mathbb{Z}^{2}$-actions by continuous automorphisms on shift-invariant subgroups of 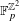$\mathbb{F}_{p}^{\mathbb{Z}^{2}}$, where 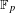$\mathbb{F}_{p}$ is the field of order 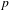$p$. These systems provide natural generalizations of Ledrappier’s system, which was the first example of a 2-mixing 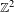$\mathbb{Z}^{2}$-action that is not 3-mixing. Extending the results from our previous work on Ledrappier’s example, we show that, under quite mild conditions (namely, 2-mixing and that the subgroup defining the system is a principal Markov subgroup), these systems are almost strongly mixing of every order in the following sense: for each order, one just needs to avoid certain effectively computable logarithmically small sets of times at which there is a substantial deviation from mixing of this order.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 5 , May 2019 , pp. 1211 - 1233
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arenas-Carmona, L., Berend, D. and Bergelson, V.. Ledrappier’s system is almost mixing of all orders. Ergod. Th. & Dynam. Sys. 28 (2008), 339–365.Google Scholar
Cassels, J. W. S.. Local Fields. Cambridge University Press, Cambridge, 1986.Google Scholar
Einsiedler, M. and Ward, T.. Asymptotic geometry of non-mixing sequences. Ergod. Th. & Dynam. Sys. 23 (2003), 75–85.Google Scholar
Fulton, W.. Algebraic Curves. An Introduction to Algebraic Geometry. Addison-Wesley Publishing Company, Advanced Book Program, Redwood City, CA, 1989, notes written with the collaboration of Richard Weiss. Reprint of 1969 original. Advanced Book Classics.Google Scholar
Kitchens, B. and Schmidt, K.. Markov subgroups of (ℤ/2ℤ)ℤ2 . Symbolic Dynamics and its Applications (New Haven, CT, 1991) (Contemporary Mathematics, 135) . American Mathematical Society, Providence, RI, 1992, pp. 265–283.Google Scholar
Ledrappier, F.. Un champ Markovien peut être d’entropie nulle et mélangeant. C. R. Math. Acad. Sci. Paris 287 (1978), 561–563.Google Scholar
Schmidt, K.. Dynamical Systems of Algebraic Origin. Birkhäuser, Basel, 1995.Google Scholar
Tijdeman, R. and Wang, L.. Sum of products of powers of given prime numbers. Pacific J. Math. 132 (1988), 177–193.Google Scholar
Voloch, J. F.. The equation ax + by = 1 in characteristic p . J. Number Theory 73 (1998), 195–200.Google Scholar