Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T01:27:17.646Z Has data issue: false hasContentIssue false
  • English
  • Français

Amenable uniformly recurrent subgroups and lattice embeddings

Part of: Topological dynamics Lie groups Locally compact groups and their algebras Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  07 February 2020

ADRIEN LE BOUDEC
ADRIEN LE BOUDEC*
Affiliation:
UCLouvain, IRMP, Chemin du Cyclotron 2, 1348 Louvain-la-Neuve, Belgium CNRS, Unité de Mathématiques Pures et Appliquées, ENS-Lyon, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study lattice embeddings for the class of countable groups $\unicode[STIX]{x1D6E4}$ defined by the property that the largest amenable uniformly recurrent subgroup 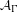${\mathcal{A}}_{\unicode[STIX]{x1D6E4}}$ is continuous. When 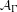${\mathcal{A}}_{\unicode[STIX]{x1D6E4}}$ comes from an extremely proximal action and the envelope of 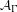${\mathcal{A}}_{\unicode[STIX]{x1D6E4}}$ is coamenable in $\unicode[STIX]{x1D6E4}$, we obtain restrictions on the locally compact groups 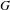$G$ that contain a copy of $\unicode[STIX]{x1D6E4}$ as a lattice, notably regarding normal subgroups of 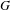$G$, product decompositions of 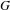$G$, and more generally dense mappings from 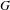$G$ to a product of locally compact groups.

Keywords

lattices in locally compact groupsstrongly proximal actionsChabauty spaceuniformly recurrent subgroupsgroups acting on trees

MSC classification

Primary: 20E08: Groups acting on trees 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.) 22D05: General properties and structure of locally compact groups 22E40: Discrete subgroups of Lie groups
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 5 , May 2021 , pp. 1464 - 1501
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bader, U., Caprace, P.-E., Gelander, T. and Mozes, S.. Lattices in amenable groups. Fund. Math. 246(3) (2019), 217–255.CrossRefGoogle Scholar
Bader, U. and Furman, A.. Boundaries, rigidity of representations, and Lyapunov exponents. Proc. Int. Congress of Mathematicians (Seoul, 2014). Vol. III. Kyung Moon Sa, Seoul, 2014, pp. 71–96.Google Scholar
Bader, U., Furman, A. and Sauer, R.. On the structure and arithmeticity of lattice envelopes. C. R. Math. Acad. Sci. Paris 353(5) (2015), 409–413.CrossRefGoogle Scholar
Bader, U. and Shalom, Y.. Factor and normal subgroup theorems for lattices in products of groups. Invent. Math. 163(2) (2006), 415–454.CrossRefGoogle Scholar
Benoist, Y. and Quint, J.-F.. Lattices in S-adic Lie groups. J. Lie Theory 24(1) (2014), 179–197.Google Scholar
Breuillard, E., Kalantar, M., Kennedy, M. and Ozawa, N.. C ∗ -simplicity and the unique trace property for discrete groups. Publ. Math. Inst. Hautes Études Sci. 126 (2017), 35–71.CrossRefGoogle Scholar
Burger, M.. On the role of totally disconnected groups in the structure of locally compact groups. New Directions in Locally Compact Groups (London Mathematical Society Lecture Note Series) . Cambridge University Press, Cambridge, 2018, pp. 1–8.Google Scholar
Burger, M. and Monod, N.. Continuous bounded cohomology and applications to rigidity theory. Geom. Funct. Anal. 12(2) (2002), 219–280.Google Scholar
Burger, M. and Mozes, S.. Finitely presented simple groups and products of trees. C. R. Acad. Sci. Paris Sér. I Math. 324(7) (1997), 747–752.CrossRefGoogle Scholar
Burger, M. and Mozes, S.. Groups acting on trees: from local to global structure. Publ. Math. Inst. Hautes Études Sci. 92 (2000), 113–150, 2000.Google Scholar
Burger, M. and Mozes, S.. Lattices in product of trees. Publ. Math. Inst. Hautes Études Sci. 92 (2000), 151–194.CrossRefGoogle Scholar
Caprace, P.-E.. Non-discrete simple locally compact groups. Proc. 7th European Congress of Mathematics. European Mathematical Society, Zürich, 2018, pp. 333–354.Google Scholar
Caprace, P.-E. and Monod, N.. Isometry groups of non-positively curved spaces: discrete subgroups. J. Topol. 2(4) (2009), 701–746.CrossRefGoogle Scholar
Caprace, P.-E. and Monod, N.. Decomposing locally compact groups into simple pieces. Math. Proc. Cambridge Philos. Soc. 150(1) (2011), 97–128.CrossRefGoogle Scholar
Caprace, P.-E. and Monod, N.. A lattice in more than two Kac–Moody groups is arithmetic. Israel J. Math. 190 (2012), 413–444.CrossRefGoogle Scholar
Caprace, P.-E. and Monod, N.. Relative amenability. Groups Geom. Dyn. 8(3) (2014), 747–774.Google Scholar
Caprace, P.-E., Reid, C. and Wesolek, P.. Approximating simple locally compact groups by their dense locally compact subgroups. Preprint, 2017, arXiv:1706.07317v1.Google Scholar
Caprace, P.-E. and Rémy, B.. Simplicity and superrigidity of twin building lattices. Invent. Math. 176(1) (2009), 169–221.CrossRefGoogle Scholar
Dahmani, F., Guirardel, V. and Osin, D.. Hyperbolically embedded subgroups and rotating families in groups acting on hyperbolic spaces. Mem. Amer. Math. Soc. 245(1156) (2017).Google Scholar
Dai, X. and Glasner, E.. On universal minimal proximal flows of topological groups. Proc. Amer. Math. Soc. 147(3) (2019), 1149–1164.Google Scholar
de la Harpe, P.. On simplicity of reduced C ∗ -algebras of groups. Bull. Lond. Math. Soc. 39(1) (2007), 1–26.CrossRefGoogle Scholar
Duchesne, B. and Monod, N.. Group actions on dendrites and curves. Preprint, 2016, arXiv:1609.00303v3.Google Scholar
Dymarz, T.. Envelopes of certain solvable groups. Comment. Math. Helv. 90(1) (2015), 195–224.CrossRefGoogle Scholar
Elek, G.. Uniformly recurrent subgroups and simple C ∗ -algebras. J. Funct. Anal. 274(6) (2018), 1657–1689.CrossRefGoogle Scholar
Erschler, A.. Poisson–Furstenberg boundaries, large-scale geometry and growth of groups. Proc. of the International Congress of Mathematicians. Volume II. Hindustan Book Agency, New Delhi, 2010, pp. 681–704.Google Scholar
Eymard, P.. Moyennes invariantes et représentations unitaires (Lecture Notes in Mathematics, 300) . Springer, Berlin, 1972.Google Scholar
Frisch, J., Schlank, T. and Tamuz, O.. Normal amenable subgroups of the automorphism group of the full shift. Preprint, 2015, arXiv:1512.00587.Google Scholar
Furman, A.. Mostow-Margulis rigidity with locally compact targets. Geom. Funct. Anal. 11(1) (2001), 30–59.Google Scholar
Furman, A.. On minimal strongly proximal actions of locally compact groups. Israel J. Math. 136 (2003), 173–187.CrossRefGoogle Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in diophantine approximation. Math. Syst. Theory 1 (1967), 1–49.CrossRefGoogle Scholar
Furstenberg, H.. Poisson boundaries and envelopes of discrete groups. Bull. Amer. Math. Soc. 73 (1967), 350–356.CrossRefGoogle Scholar
Furstenberg, H.. Boundary theory and stochastic processes on homogeneous spaces. Harmonic Analysis on Homogeneous Spaces (Proc. Sympos. Pure Math., Vol. XXVI, Williams Coll., Williamstown, MA, 1972). American Mathematical Society, Providence, RI, 1973, pp. 193–229.Google Scholar
Furstenberg, H.. Rigidity and cocycles for ergodic actions of semisimple Lie groups (after G. A. Margulis and R. Zimmer). Bourbaki Seminar, Vol. 1979/80 (Lecture Notes in Mathematics, 842) . Springer, Berlin, 1981, pp. 273–292.Google Scholar
Ghys, É.. Groups acting on the circle. Enseign. Math. (2) 47(3–4) (2001), 329–407.Google Scholar
Glasner, E. and Weiss, B.. Uniformly recurrent subgroups. Recent Trends in Ergodic Theory and Dynamical Systems (Contemporary Mathematics, 631) . American Mathematical Society, Providence, RI, 2015, pp. 63–75.Google Scholar
Glasner, S.. Topological dynamics and group theory. Trans. Amer. Math. Soc. 187 (1974), 327–334.CrossRefGoogle Scholar
Glasner, S.. Compressibility properties in topological dynamics. Amer. J. Math. 97 (1975), 148–171.CrossRefGoogle Scholar
Glasner, S.. Proximal Flows (Lecture Notes in Mathematics, 517) . Springer, Berlin, 1976.Google Scholar
Gruenberg, K. W.. Residual properties of infinite soluble groups. Proc. Lond. Math. Soc. (3) 7 (1957), 29–62.Google Scholar
Guivarc’h, Y.. Croissance polynomiale et périodes des fonctions harmoniques. Bull. Soc. Math. France 101 (1973), 333–379.CrossRefGoogle Scholar
Hewitt, E. and Ross, K.. Abstract harmonic analysis. Structure of Topological Groups, Integration Theory, Group Representations. Vol. I (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 115) . 2nd edn. Springer, Berlin, 1979.Google Scholar
Jenkins, J. W.. Growth of connected locally compact groups. J. Funct. Anal. 12 (1973), 113–127.CrossRefGoogle Scholar
Jolissaint, P. and Robertson, G.. Simple purely infinite C ∗ -algebras and n-filling actions. J. Funct. Anal. 175(1) (2000), 197–213.Google Scholar
Kalantar, M. and Kennedy, M.. Boundaries of reduced C ∗ -algebras of discrete groups. J. Reine Angew. Math. 727 (2017), 247–267.Google Scholar
Kawabe, T.. Uniformly recurrent subgroups and the ideal structure of reduced crossed products. Preprint, 2017, arXiv:1701.03413.Google Scholar
Kennedy, M.. Characterizations of $C^{\ast }$ -simplicity. Preprint, 2015, arXiv:1509.01870v3.Google Scholar
Laca, M. and Spielberg, J.. Purely infinite C ∗ -algebras from boundary actions of discrete groups. J. Reine Angew. Math. 480 (1996), 125–139.Google Scholar
Le Boudec, A.. Groups acting on trees with almost prescribed local action. Comment. Math. Helv. 91(2) (2016), 253–293.CrossRefGoogle Scholar
Le Boudec, A.. C ∗ -simplicity and the amenable radical. Invent. Math. 209(1) (2017), 159–174.CrossRefGoogle Scholar
Le Boudec, A.. Simple groups and irreducible lattices in wreath products. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2020.5.CrossRefGoogle Scholar
Le Boudec, A. and Matte Bon, N.. Subgroup dynamics and C ∗ -simplicity of groups of homeomorphisms. Ann. Sci. Éc. Norm. Supér. (4) 51(3) (2018), 557–602.CrossRefGoogle Scholar
Le Boudec, A. and Wesolek, P.. Commensurated subgroups in tree almost automorphism groups. Groups Geom. Dyn. 13(1) (2019), 1–30.CrossRefGoogle Scholar
Losert, V.. On the structure of groups with polynomial growth. Math. Z. 195(1) (1987), 109–117.CrossRefGoogle Scholar
Malcev, A.. On isomorphic matrix representations of infinite groups. Rec. Math. [Mat. Sbornik] N.S. 8(50) (1940), 405–422.Google Scholar
Margulis, G.. Free subgroups of the homeomorphism group of the circle. C. R. Acad. Sci. Paris Sér. I Math. 331(9) (2000), 669–674.CrossRefGoogle Scholar
Margulis, G. A.. Discrete Subgroups of Semisimple Lie Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 17) . Springer, Berlin, 1991.CrossRefGoogle Scholar
Matte Bon, N.. Rigidity properties of full groups of pseudogroups over the cantor set. Preprint, 2018, arXiv:1801.10133.Google Scholar
Matte Bon, N. and Tsankov, T.. Realizing uniformly recurrent subgroups. Preprint, 2017, arXiv:1702.07101.Google Scholar
Monod, N. and Popa, S.. On co-amenability for groups and von Neumann algebras. C. R. Math. Acad. Sci. Soc. R. Can. 25(3) (2003), 82–87.Google Scholar
Monod, N. and Shalom, Y.. Cocycle superrigidity and bounded cohomology for negatively curved spaces. J. Differential Geom. 67(3) (2004), 395–455.Google Scholar
Montgomery, D. and Zippin, L.. Topological Transformation Groups. Interscience Publishers, New York, 1955.Google Scholar
Nekrashevych, V.. Finitely presented groups associated with expanding maps. Preprint, 2013, arXiv:1312.5654v1.Google Scholar
Pays, I. and Valette, A.. Sous-groupes libres dans les groupes d’automorphismes d’arbres. Enseign. Math. (2) 37(1–2) (1991), 151–174.Google Scholar
Radu, N.. New simple lattices in products of trees and their projections. Preprint, 2017, arXiv:1712.01091. With an appendix by P-E. Caprace.Google Scholar
Raghunathan, M. S.. Discrete Subgroups of Lie Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, 68) . Springer, Berlin, 1972.CrossRefGoogle Scholar
Rattaggi, D.. Computations in groups acting on a product of trees: Normal subgroup structures and quaternion lattices. Thesis (Dr. sc. math.), Eidgenössische Technische Hochschule Zürich, Switzerland, 2004. Available at ProQuest LLC, Ann Arbor, MI.Google Scholar
Rémy, B.. Construction de réseaux en théorie de Kac-Moody. C. R. Acad. Sci. Paris Sér. I Math. 329(6) (1999), 475–478.CrossRefGoogle Scholar
Shalom, Y.. Rigidity of commensurators and irreducible lattices. Invent. Math. 141(1) (2000), 1–54.CrossRefGoogle Scholar
Tits, J.. Sur le groupe des automorphismes d’un arbre. Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham). Springer, New York, 1970, pp. 188–211.CrossRefGoogle Scholar
Vorobets, Y.. Notes on the Schreier graphs of the Grigorchuk group. Dynamical Systems and Group Actions (Contemporary Mathematics, 567) . American Mathematical Society, Providence, RI, 2012, pp. 221–248.Google Scholar
Wise, D.. Non-positively curved squared complexes: aperiodic tilings and non-residually finite groups. PhD Thesis, Princeton University, 1996. Available at ProQuest LLC, Ann Arbor, MI.Google Scholar