Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T00:24:48.006Z Has data issue: false hasContentIssue false
  • English
  • Français

The ambient structure of basic sets†

Published online by Cambridge University Press:  14 October 2010

A. Löffler
A. Löffler
Affiliation:
Graduiertenkolleg, FB Wirtschaftswissenschaften, Freie Universität Berlin, Boltzmannstrasse 20, Berlin, 14195, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Λ be a basic set of an Axiom A diffeomorphism of a compact Riemannian manifold M without boundary. If ε is small enough one can find by local product structure that for x ε Λ there is a neighborhood V(x) in M such that V ∩ Λ is homeomorphic to 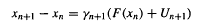. The author proves that this homeomorphism can be extended to a homeomorphism of V onto .

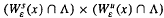Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 15 , Issue 6 , December 1995 , pp. 1183 - 1188
Copyright
Copyright © Cambridge University Press 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bothe, H. G.. The ambient structure of expanding attractors. Math. Nachrichten 107 (1982), 327–348.CrossRefGoogle Scholar
[2]Hirsch, H. W. and Smale, S.. Stable manifolds and hyperbolic sets, in: global analysis. Proc. Symposia in Pure Mathematics. Vol. XIV. Rhode Island 1970, 133–164.CrossRefGoogle Scholar
[3]Hirsch, M., Palis, J., Pugh, C. and Shub, M.. Neighborhoods of hyperbolic sets. Invent. Math. 9 (1970), 121–134.CrossRefGoogle Scholar
[4]Hirsch, M.. Differential Topology. Springer Graduate Texts in Mathematics 33. Springer, Berlin-New York-Heidelberg, 1976.Google Scholar
[5]Newhouse, S. E.. Lectures on dynamical systems. Dyn. systems C.I.M.E. Lectures Bressanone 1978. Progress in Mathematics 8, 1–115.Google Scholar
[6]Robinson, C.. Structural stability of C1 diffeomorphisms. J. Diff. Eq. 22 (1976), 28–73.CrossRefGoogle Scholar
[7]Shub, M.. Global Stability of Dynamical Systems. Springer: Berlin-New York-Heidelberg-Tokyo, 1987.CrossRefGoogle Scholar
[8]Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.CrossRefGoogle Scholar