Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T17:29:14.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost Mathieu operators with completely resonant phases

Part of: Random dynamical systems Smooth dynamical systems: general theory

Published online by Cambridge University Press:  19 December 2018

WENCAI LIU Open the ORCID record for WENCAI LIU [Opens in a new window]
WENCAI LIU*
Affiliation:
Department of Mathematics, University of California, Irvine, CA 92697-3875, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 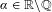$\unicode[STIX]{x1D6FC}\in \mathbb{R}\backslash \mathbb{Q}$ and 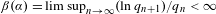$\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6FC})=\limsup _{n\rightarrow \infty }(\ln q_{n+1})/q_{n}<\infty$, where 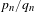$p_{n}/q_{n}$ is the continued fraction approximation to $\unicode[STIX]{x1D6FC}$. Let 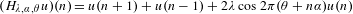$(H_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}u)(n)=u(n+1)+u(n-1)+2\unicode[STIX]{x1D706}\cos 2\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D703}+n\unicode[STIX]{x1D6FC})u(n)$ be the almost Mathieu operator on 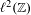$\ell ^{2}(\mathbb{Z})$, where 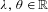$\unicode[STIX]{x1D706},\unicode[STIX]{x1D703}\in \mathbb{R}$. Avila and Jitomirskaya [The ten Martini problem. Ann. of Math. (2), 170(1) (2009), 303–342] conjectured that, for 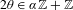$2\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6FC}\mathbb{Z}+\mathbb{Z}$, 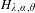$H_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}$ satisfies Anderson localization if 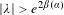$|\unicode[STIX]{x1D706}|>e^{2\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6FC})}$. In this paper, we develop a method to treat simultaneous frequency and phase resonances and obtain that, for 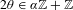$2\unicode[STIX]{x1D703}\in \unicode[STIX]{x1D6FC}\mathbb{Z}+\mathbb{Z}$, 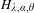$H_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}}$ satisfies Anderson localization if 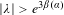$|\unicode[STIX]{x1D706}|>e^{3\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6FC})}$.

Keywords

arithmetic and algebraic dynamicsclassical ergodic theorynumber theory

MSC classification

Primary: 37H15: Multiplicative ergodic theory, Lyapunov exponents
Secondary: 37C55: Periodic and quasiperiodic flows and diffeomorphisms
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 7 , July 2020 , pp. 1875 - 1893
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A. and Jitomirskaya, S.. Solving the ten Martini problem. Mathematical Physics of Quantum Mechanics (Lecture Notes in Physics, 690). Springer, Berlin, 2006, pp. 5–16.Google Scholar
Avila, A. and Jitomirskaya, S.. The ten Martini problem. Ann. of Math. (2) 170(1) (2009), 303–342.Google Scholar
Avila, A. and Jitomirskaya, S.. Almost localization and almost reducibility. J. Eur. Math. Soc. 12(1) (2010), 93–131.Google Scholar
Avila, A., Jitomirskaya, S. and Zhou, Q.. Second phase transition line. Math. Ann. 370(1–2) (2018), 271–285.Google Scholar
Avila, A., You, J. and Zhou, Q.. Dry ten Martini problem in non-critical case. Preprint.Google Scholar
Avila, A., You, J. and Zhou, Q.. Sharp phase transitions for the almost Mathieu operator. Duke Math. J. 166(14) (2017), 2697–2718.Google Scholar
Bellissard, J., Lima, R. and Testard, D.. Almost periodic Schrödinger operators. Mathematics+ Physics (Lectures on Recent Results, 1). World Scientific, Singapore, 1985, pp. 1–64.Google Scholar
Berezanskii, J. M.. Expansions in Eigenfunctions of Self-Adjoint Operators (Translations of Mathematical Monographs, 17). American Mathematical Society, Providence, RI, 1968.Google Scholar
Bourgain, J.. Green’s Function Estimates for Lattice Schrödinger Operators and Applications (Annals of Mathematics Studies, 158). Princeton University Press, Princeton, NJ, 2005.Google Scholar
Bourgain, J. and Goldstein, M.. On nonperturbative localization with quasi-periodic potential. Ann. Math. 152(3) (2000), 835–879.Google Scholar
Bourgain, J., Goldstein, M. and Schlag, W.. Anderson localization for Schrödinger operators on Z2 with quasi-periodic potential. Acta Math. 188(1) (2002), 41–86.Google Scholar
Bourgain, J. and Jitomirskaya, S.. Absolutely continuous spectrum for 1D quasiperiodic operators. Invent. Math. 148(3) (2002), 453–463.Google Scholar
Chulaevsky, V. and Delyon, F.. Purely absolutely continuous spectrum for almost Mathieu operators. J. Statist. Phys. 55(5–6) (1989), 1279–1284.Google Scholar
Dinaburg, E. and Sinai, Y. G.. The one-dimensional Schrödinger equation with a quasiperiodic potential. Funct. Anal. Appl. 9(4) (1975), 279–289.Google Scholar
Eliasson, L. H.. Floquet solutions for the 1-dimensional quasi-periodic Schrödinger equation. Commun. Math. Phys. 146(3) (1992), 447–482.Google Scholar
Fröhlich, J., Spencer, T. and Wittwer, P.. Localization for a class of one dimensional quasi-periodic Schrödinger operators. Commun. Math. Phys. 132(1) (1990), 5–25.Google Scholar
Gordon, A. Y.. The point spectrum of the one-dimensional Schrödinger operator. Uspekhi Mat. Nauk 31(4) (1976), 257–258.Google Scholar
Gordon, A. Y., Jitomirskaya, S., Last, Y. and Simon, B.. Duality and singular continuous spectrum in the almost Mathieu equation. Acta Math. 178(2) (1997), 169–183.Google Scholar
Hadj Amor, S.. Hölder continuity of the rotation number for quasi-periodic co-cycles in SL(2, ℝ). Commun. Math. Phys. 287(2) (2009), 565–588.Google Scholar
Han, R.. Dry ten Martini problem for the non-self-dual extended Harper’s model. Trans. Amer. Math. Soc. 370(1) (2018), 197–217.Google Scholar
Han, R. and Jitomirskaya, S.. Full measure reducibility and localization for quasiperiodic Jacobi operators: a topological criterion. Adv. Math. 319 (2017), 224–250.Google Scholar
Jitomirskaya, S.. Almost everything about the almost Mathieu operator. II. XIth International Congress of Mathematical Physics (Paris, 1994). International Press, Cambridge, MA, 1995, pp. 373–382.Google Scholar
Jitomirskaya, S.. Metal-insulator transition for the almost Mathieu operator. Ann. Math. 150(3) (1999), 1159–1175.Google Scholar
Jitomirskaya, S. and Kachkovskiy, I.. L 2 -reducibility and localization for quasiperiodic operators. Math. Res. Lett. 23(2) (2016), 431–444.Google Scholar
Jitomirskaya, S., Koslover, D. A. and Schulteis, M. S.. Localization for a family of one-dimensional quasiperiodic operators of magnetic origin. Ann. Henri Poincaré 6(1) (2005), 103–124.Google Scholar
Jitomirskaya, S. and Liu, W.. Arithmetic spectral transitions for the Maryland model. Commun. Pure Appl. Math. 70(6) (2017), 1025–1051.Google Scholar
Jitomirskaya, S. and Liu, W.. Universal hierarchical structure of quasiperiodic eigenfunctions. Ann. of Math. (2) 187(3) (2018), 721–776.Google Scholar
Jitomirskaya, S. and Liu, W.. Universal reflective-hierarchical structure of quasiperiodic eigenfunctions and sharp spectral transition in phase. Preprint, 2018, arXiv:1802.00781.Google Scholar
Jitomirskaya, S. and Marx, C. A.. Analytic quasi-periodic Schrödinger operators and rational frequency approximants. Geom. Funct. Anal. 22(5) (2012), 1407–1443.Google Scholar
Jitomirskaya, S. and Simon, B.. Operators with singular continuous spectrum. III. Almost periodic Schrödinger operators. Commun. Math. Phys. 165(1) (1994), 201–205.Google Scholar
Jitomirskaya, S. and Zhang, S.. Quantitative continuity of singular continuous spectral measures and arithmetic criteria for quasiperiodic Schrödinger operators. Preprint, 2015, arXiv:1510.07086.Google Scholar
Johnson, R. and Moser, J.. The rotation number for almost periodic potentials. Commun. Math. Phys. 84(3) (1982), 403–438.Google Scholar
Krasovsky, I.. Central spectral gaps of the almost Mathieu operator. Commun. Math. Phys. 351(1) (2017), 419–439.Google Scholar
Last, Y.. Spectral theory of Sturm–Liouville operators on infinite intervals: a review of recent developments. Sturm–Liouville Theory. Birkhäuser, Basel, 2005, pp. 99–120.Google Scholar
Last, Y. and Shamis, M.. Zero Hausdorff dimension spectrum for the almost Mathieu operator. Commun. Math. Phys. 348(3) (2016), 729–750.Google Scholar
Liu, W. and Shi, Y.. Upper bounds on the spectral gaps of quasi-periodic Schrödinger operators with Liouville frequencies. J. Spectr. Theory, to appear.Google Scholar
Liu, W. and Yuan, X.. Anderson localization for the almost Mathieu operator in the exponential regime. J. Spectr. Theory 5(1) (2015), 89–112.Google Scholar
Liu, W. and Yuan, X.. Anderson localization for the completely resonant phases. J. Funct. Anal. 268(3) (2015), 732–747.Google Scholar
Liu, W. and Yuan, X.. Spectral gaps of almost Mathieu operators in the exponential regime. J. Fractal Geom. 2(1) (2015), 1–51.Google Scholar
Marx, C. A. and Jitomirskaya, S.. Dynamics and spectral theory of quasi-periodic Schrödinger-type operators. Ergod. Th. & Dynam. Sys. 37(8) (2017), 2353–2393.Google Scholar
Moser, J. and Pöschel, J.. An extension of a result by Dinaburg and Sinai on quasi-periodic potentials. Comment. Math. Helv. 59(1) (1984), 39–85.Google Scholar
Puig, J.. Cantor spectrum for the almost Mathieu operator. Commun. Math. Phys. 244(2) (2004), 297–309.Google Scholar
Puig, J.. A nonperturbative Eliasson’s reducibility theorem. Nonlinearity 19(2) (2006), 355–376.Google Scholar
Simon, B.. Almost periodic Schrödinger operators: a review. Adv. Appl. Math. 3(4) (1982), 463–490.Google Scholar
Yang, F.. Spectral transition line for the extended Harper’s model in the positive Lyapunov exponent regime. J. Funct. Anal. 275(3) (2018), 712–734.Google Scholar