Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Assani, I.
Lesigne, E.
and
Rudolph, D.
1995.
Wiener-Wintner return-times ergodic theorem.
Israel Journal of Mathematics,
Vol. 92,
Issue. 1-3,
p.
375.
Walters, Peter
1996.
Topological Wiener–Wintner ergodic theorems and a randomL2ergodic theorem.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 1,
p.
179.
El Houcein, El Abdalaoui
2021.
van der Corput inequality for real line and Wiener-Wintner theorem for amenable groups.
Constructive Mathematical Analysis,
Vol. 4,
Issue. 4,
p.
420.


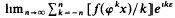 exists for all ε ℝ.
exists for all ε ℝ.