Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yoshimoto, Takeshi
2020.
Modulated ( C , α ) -ergodic theorems with non-integral orders for Dunford–Schwartz operators.
Illinois Journal of Mathematics,
Vol. 64,
Issue. 4,
Lian, Zhengxing
and
Shi, Ruxi
2021.
A counter-example for polynomial version of Sarnak's conjecture.
Advances in Mathematics,
Vol. 384,
Issue. ,
p.
107765.
Buczolich, Zoltán
and
Eisner, Tanja
2021.
Divergence of weighted square averages in L1.
Advances in Mathematics,
Vol. 384,
Issue. ,
p.
107727.
Mukhamedov, Farrukh
2021.
Weighted laws of large numbers and convergence of weighted ergodic averages on vector valued $$L_p$$-spaces.
Advances in Operator Theory,
Vol. 6,
Issue. 3,
Bárány, Balázs
Rams, Michaƚ
and
Shi, Ruxi
2022.
On the multifractal spectrum of weighted Birkhoff averages.
Discrete & Continuous Dynamical Systems,
Vol. 42,
Issue. 5,
p.
2461.
Fan, Aihua
Fan, Shilei
Ryzhikov, Valery V.
and
Shen, Weixiao
2022.
Bohr chaoticity of topological dynamical systems.
Mathematische Zeitschrift,
Vol. 302,
Issue. 2,
p.
1127.
Darwiche, Ahmad
and
Schneider, Dominique
2023.
On the rate of convergence of weighted oscillating ergodic averages.
Stochastics and Dynamics,
Vol. 23,
Issue. 02,
Tong, Zhicheng
and
Li, Yong
2024.
Exponential convergence of the weighted Birkhoff average.
Journal de Mathématiques Pures et Appliquées,
Vol. 188,
Issue. ,
p.
470.
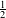 $\frac{1}{2}$ are good sequences of weights for the ergodic theorem, and that the ergodic sums weighted by a sequence of strong Gelfond property are well controlled almost everywhere. We prove that for any
$\frac{1}{2}$ are good sequences of weights for the ergodic theorem, and that the ergodic sums weighted by a sequence of strong Gelfond property are well controlled almost everywhere. We prove that for any  $q$-multiplicative sequence, the Gelfond property implies the strong Gelfond property and that sequences realized by dynamical systems can be fully oscillating and have the Gelfond property.
$q$-multiplicative sequence, the Gelfond property implies the strong Gelfond property and that sequences realized by dynamical systems can be fully oscillating and have the Gelfond property.