Published online by Cambridge University Press: 13 August 2013
Abért and Weiss have shown that the Bernoulli shift 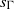 ${s}_{\Gamma } $ of a countably infinite group
${s}_{\Gamma } $ of a countably infinite group 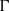 $\Gamma $ is weakly contained in any free measure preserving action
$\Gamma $ is weakly contained in any free measure preserving action  $\boldsymbol{a}$ of
$\boldsymbol{a}$ of 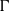 $\Gamma $. Proving a conjecture of Ioana, we establish a strong version of this result by showing that
$\Gamma $. Proving a conjecture of Ioana, we establish a strong version of this result by showing that 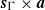 ${\boldsymbol{s}}_{\Gamma } \times \boldsymbol{a}$ is weakly equivalent to
${\boldsymbol{s}}_{\Gamma } \times \boldsymbol{a}$ is weakly equivalent to  $\boldsymbol{a}$. Using random Bernoulli shifts introduced by Abért, Glasner, and Virag, we generalize this to non-free actions, replacing
$\boldsymbol{a}$. Using random Bernoulli shifts introduced by Abért, Glasner, and Virag, we generalize this to non-free actions, replacing 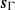 ${\boldsymbol{s}}_{\Gamma } $ with a random Bernoulli shift associated to an invariant random subgroup, and replacing the product action with a relatively independent joining. The result for free actions is used along with the theory of Borel reducibility and Hjorth’s theory of turbulence to show that, on the weak equivalence class of a free measure preserving action, the equivalence relations of isomorphism, weak isomorphism, and unitary equivalence are not classifiable by countable structures. This in particular shows that there are no free weakly rigid actions, that is, actions whose weak equivalence class and isomorphism class coincide, answering negatively a question of Abért and Elek. We also answer a question of Kechris regarding two ergodic theoretic properties of residually finite groups. A countably infinite residually finite group
${\boldsymbol{s}}_{\Gamma } $ with a random Bernoulli shift associated to an invariant random subgroup, and replacing the product action with a relatively independent joining. The result for free actions is used along with the theory of Borel reducibility and Hjorth’s theory of turbulence to show that, on the weak equivalence class of a free measure preserving action, the equivalence relations of isomorphism, weak isomorphism, and unitary equivalence are not classifiable by countable structures. This in particular shows that there are no free weakly rigid actions, that is, actions whose weak equivalence class and isomorphism class coincide, answering negatively a question of Abért and Elek. We also answer a question of Kechris regarding two ergodic theoretic properties of residually finite groups. A countably infinite residually finite group 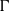 $\Gamma $ is said to have property
$\Gamma $ is said to have property 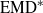 ${\text{EMD} }^{\ast } $ if the action
${\text{EMD} }^{\ast } $ if the action 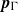 ${\boldsymbol{p}}_{\Gamma } $ of
${\boldsymbol{p}}_{\Gamma } $ of 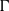 $\Gamma $ on its profinite completion weakly contains all ergodic measure preserving actions of
$\Gamma $ on its profinite completion weakly contains all ergodic measure preserving actions of 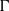 $\Gamma $, and
$\Gamma $, and 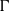 $\Gamma $ is said to have property
$\Gamma $ is said to have property 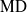 $\text{MD} $ if
$\text{MD} $ if 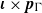 $\boldsymbol{\iota} \times {\boldsymbol{p}}_{\Gamma } $ weakly contains all measure preserving actions of
$\boldsymbol{\iota} \times {\boldsymbol{p}}_{\Gamma } $ weakly contains all measure preserving actions of 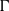 $\Gamma $, where
$\Gamma $, where  $\boldsymbol{\iota} $ denotes the identity action on a standard non-atomic probability space. Kechris has shown that
$\boldsymbol{\iota} $ denotes the identity action on a standard non-atomic probability space. Kechris has shown that 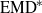 ${\text{EMD} }^{\ast } $ implies
${\text{EMD} }^{\ast } $ implies 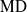 $\text{MD} $ and asked if the two properties are actually equivalent. We provide a positive answer to this question by studying the relationship between convexity and weak containment in the space of measure preserving actions.
$\text{MD} $ and asked if the two properties are actually equivalent. We provide a positive answer to this question by studying the relationship between convexity and weak containment in the space of measure preserving actions.