Article contents
Volume hyperbolicity and wildness
Published online by Cambridge University Press: 19 September 2016
Abstract
It is known that volume hyperbolicity (partial hyperbolicity and uniform expansion or contraction of the volume in the extremal bundles) is a necessary condition for robust transitivity or robust chain recurrence and hence for tameness. In this paper, on any  $3$-manifold we build examples of quasi-attractors which are volume hyperbolic and wild at the same time. As a main corollary, we see that, for any closed
$3$-manifold we build examples of quasi-attractors which are volume hyperbolic and wild at the same time. As a main corollary, we see that, for any closed  $3$-manifold
$3$-manifold 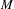 $M$, the space
$M$, the space 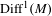 $\text{Diff}^{1}(M)$ admits a non-empty open set where every
$\text{Diff}^{1}(M)$ admits a non-empty open set where every 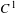 $C^{1}$-generic diffeomorphism has no attractors or repellers. The main tool of our construction is the notion of flexible periodic points introduced in the authors’ previous paper. In order to eject the flexible points from the quasi-attractor, we control the topology of the quasi-attractor using the notion of partially hyperbolic filtrating Markov partitions, which we introduce in this paper.
$C^{1}$-generic diffeomorphism has no attractors or repellers. The main tool of our construction is the notion of flexible periodic points introduced in the authors’ previous paper. In order to eject the flexible points from the quasi-attractor, we control the topology of the quasi-attractor using the notion of partially hyperbolic filtrating Markov partitions, which we introduce in this paper.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 2
- Cited by


