Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-18T10:58:52.179Z Has data issue: false hasContentIssue false
  • English
  • Français

Twisted cohomological equations for translation flows

Part of: Two-dimensional theory Smooth dynamical systems: general theory Low-dimensional dynamical systems Miscellaneous topics of analysis in the complex domain Ergodic theory

Published online by Cambridge University Press:  22 October 2021

GIOVANNI FORNI
GIOVANNI FORNI*
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove by methods of harmonic analysis a result on the existence of solutions for twisted cohomological equations on translation surfaces with loss of derivatives at most 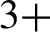$3+$ in Sobolev spaces. As a consequence we prove that product translation flows on (three-dimensional) translation manifolds which are products of a (higher-genus) translation surface with a (flat) circle are stable in the sense of A. Katok. In turn, our result on product flows implies a stability result of time-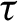 $\tau $ maps of translation flows on translation surfaces.

Keywords

translation surfaces and flowstwisted cohomological equationstwisted invariant distributionsSobolev estimates

MSC classification

Primary: 37C10: Vector fields, flows, ordinary differential equations 37E35: Flows on surfaces 37A20: Orbit equivalence, cocycles, ergodic equivalence relations
Secondary: 30E20: Integration, integrals of Cauchy type, integral representations of analytic functions 31A20: Boundary behavior (theorems of Fatou type, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 3: Anatole Katok Memorial Issue Part 2: Special Issue of Ergodic Theory and Dynamical Systems , March 2022 , pp. 881 - 916
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to Anatole Katok, who taught us how to think

References

Adam, A. and Baladi, V.. Horocycle averages on closed manifolds and transfer operators. Preprint, 2021, arXiv:1809.04062v3.Google Scholar
Aranson, S. H. and Grines, V. Z.. On some invariants of dynamical systems on two-dimensional manifolds (necessary and sufficient conditions for the topological equivalence of transitive dynamical systems). Mat. Sb. 90(132) (1973), 372–402. Engl. Transl. Math. USSR Sb. 19 (1973), 365–393.Google Scholar
Bufetov, A. I. and Solomyak, B.. On the modulus of continuity for spectral measures in substitution dynamics. Adv. Math. 260 (2014), 84–129.CrossRefGoogle Scholar
Bufetov, A. I. and Solomyak, B.. The Hölder property for the spectrum of translation flows in genus two. Israel J. Math. 223(1) (2018), 205–259.CrossRefGoogle Scholar
Bufetov, A. I. and Solomyak, B.. On ergodic averages for parabolic product flows. Bull. Soc. Math. France 146(4) (2018), 675–690.CrossRefGoogle Scholar
Bufetov, A. I. and Solomyak, B.. A spectral cocycle for substitution systems and translation flows. J. Anal. Math. 141 (2020), 165–205.CrossRefGoogle Scholar
Bufetov, A. I. and Solomyak, B.. Hölder regularity for the spectrum of translation flows. J. Éc. Polytech. Math. 8 (2021), 279–310.CrossRefGoogle Scholar
Chaika, J. and Eskin, A.. Every flat surface is Birkhoff and Oseledets generic in almost every direction. J. Mod. Dyn. 9 (2015), 1–23.CrossRefGoogle Scholar
Demailly, J.-P.. Théorie de Hodge ${L}^2$ et théorèmes d′annulation. Introduction à la Théorie de Hodge (Panoramas et Synthèses, 3). Société Mathématique de France, Paris, 1996, pp. 3–111.Google Scholar
Eskin, A. and Mirzakhani, M.. Invariant and stationary measures for the $\mathbf{SL}\left(2,\mathbb{R}\right)$ action on moduli space. Publ. Math. Inst. Hautes Études Sci. 127(1) (2018), 95–324.CrossRefGoogle Scholar
Eskin, A., Mirzakhani, M. and Mohammadi, A.. Isolation, equidistribution, and orbit closures for the $\mathbf{SL}\left(2,\mathbb{R}\right)$ action on moduli space. Ann. of Math. (2) 182 (2015), 673–721.CrossRefGoogle Scholar
Forni, G.. Solutions of the cohomological equation for area-preserving flows on compact surfaces of higher genus. Ann. of Math. (2) 146(2) (1997), 295–344.CrossRefGoogle Scholar
Forni, G.. Deviation of ergodic averages for area-preserving flows on surfaces of higher genus. Ann. of Math (2) 155(1) (2002), 1–103.CrossRefGoogle Scholar
Forni, G.. Sobolev regularity of solutions of the cohomological equation. Ergod. Th. & Dynam. Sys. 41 (2020), 1–105.Google Scholar
Forni, G.. On the Greenfield–Wallach and Katok conjectures. Geometric and Probabilistic Structures in Dynamics (Contemporary Mathematics, 469). Eds. Burns, K., Dolgopyat, D. and Pesin, Y.. American Mathematical Society, Providence RI, 2008, pp. 197–215.CrossRefGoogle Scholar
Forni, G.. Twisted translation flows and effective weak mixing. Preprint, 2021, arXiv:1908.11040v1. J. Eur. Math. Soc., to appear.Google Scholar
Flaminio, L., Forni, G. and Tanis, J.. Effective equidistribution of twisted horocycle flows and horocycle maps. Geom. Funct. Anal. 26(5) (2016), 1359–1448.CrossRefGoogle Scholar
Faure, F. and Guillarmou, C.. Horocyclic invariance of Ruelle resonant states for contact Anosov flows in dimension 3. Math. Res. Lett. 25(5) (2018), 1405–1427.Google Scholar
Faure, F., Gouëzel, S. and Lanneau, E.. Ruelle spectrum of linear pseudo-Anosov maps. J. Éc. polytech. Math. 6 (2019), 811–877.CrossRefGoogle Scholar
Filip, S.. Semisimplicity and rigidity of the Kontsevich–Zorich cocycle. Invent. Math. 205(3) (2016), 617–670.CrossRefGoogle Scholar
Flaminio, L. and Forni, G.. Invariant distributions and time averages for horocycle flows. Duke Math. J. 119(3) (2003), 465–526.CrossRefGoogle Scholar
Flaminio, L. and Forni, G.. Equidistribution of nilflows and applications to theta sums. Ergod. Th. & Dynam. Sys. 26(2) (2006), 409–433.CrossRefGoogle Scholar
Flaminio, L. and Forni, G.. On the cohomological equation for nilflows. J. Mod. Dyn. 1(1) (2007), 37–60.CrossRefGoogle Scholar
Flaminio, L. and Forni, G.. On effective equidistribution for higher step nilflows. Preprint, 2014, arXiv:1407.3640v1.Google Scholar
Fatou, P.. Séries trigonométriques et séries de Taylor. Acta Math. 30 (1906), 335–400.CrossRefGoogle Scholar
Giulietti, P. and Liverani, C.. Parabolic dynamics and anisotropic Banach spaces. J. Eur. Math. Soc. (JEMS) 21(9) (2019), 2793–2858.CrossRefGoogle Scholar
Goldman, W.. The symplectic nature of fundamental groups of surfaces. Adv. Math. 54(2) (1984), 200–225.CrossRefGoogle Scholar
Green, B. and Tao, T.. The quantitative behaviour of polynomial orbits on nilmanifolds. Ann. of Math. (2) 175 (2012), 465–540.CrossRefGoogle Scholar
Hardy, G. H. and Littlewood, J. E.. A maximal theorem with function-theoretic applications. Acta Math. 54 (1930), 81–116.CrossRefGoogle Scholar
Katok, A. B.. Cocycles, cohomology and combinatorial constructions in ergodic theory. Smooth Ergodic Theory and Its Applications (Seattle, WA, 1999) (Proceedings of Symposia in Pure Mathematics, 69). American Mathematical Society, Providence, RI, 2001, in collaboration with E. A. Robinson, Jr, pp. 107–173.CrossRefGoogle Scholar
Katok, A. B.. Combinatorial Constructions in Ergodic Theory and Dynamics (University Lecture Series, 30). American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
Lions, J. L. and Magenes, E.. Problèmes aux Limites non Homogènes et Applications. Vol. 1. Dunod, Paris, 1968.Google Scholar
Maier, A. G.. Trajectories on the closed orientable surfaces. Mat. Sb. 12(54) (1943), 71–84 (in Russian).Google Scholar
Marmi, S., Moussa, P. and Yoccoz, J.-C.. The cohomological equation for Roth-type interval exchange maps. J. Amer. Math. Soc. 18(4) (2005), 823–872.CrossRefGoogle Scholar
Marmi, S. and Yoccoz, J.-C.. Hölder regularity of the solutions of the cohomological equation for Roth type interval exchange maps. Comm. Math. Phys. 344(1) (2016), 117–139.CrossRefGoogle Scholar
Nelson, E.. Analytic vectors. Ann. of Math. (2) 70 (1959), 572–615.CrossRefGoogle Scholar
Rudin, W.. Real and Complex Analysis, 3rd edn. McGraw-Hill, New York, 1987.Google Scholar
Riesz, F.. Über die Randwerte einer analytischen Funktion. Math. Z. 18 (1923), 87–95.CrossRefGoogle Scholar
Smirnov, V.. Sur les valeurs limites des fonctions régulières à l’intérieur d′un cercle. J. Soc. Physico-Math. Leningrad 2 (1929), 22–37.Google Scholar
Stein, E. M. and Weiss, G.. Introduction to Fourier Analysis on Euclidean Spaces. Princeton University Press, Princeton, NJ, 1971.Google Scholar
Tanis, J.. The cohomological equation and invariant distributions for horocycle maps. Ergod. Th. & Dynam. Sys. 12 (2012), 1–42.Google Scholar
Voisin, C.. Hodge Theory and Complex Algebraic Geometry, I (Cambridge Studies in Advanced Mathematics, 76). Cambridge University Press, Cambridge, 2002.CrossRefGoogle Scholar
Yosida, K.. Functional Analysis, 6th edn. Springer-Verlag, Berlin, 1980.Google Scholar
Zygmund, A.. Trigonometric Series. Cambridge University Press, Cambridge, 1959 (reprinted in 1990).Google Scholar