Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:56:56.472Z Has data issue: false hasContentIssue false
  • English
  • Français

θ-transformations, θ-shifts and limit theorems for some Riesz-Raikov sums

Published online by Cambridge University Press:  19 September 2008

Bernard Petit
Bernard Petit
Affiliation:
Département de Mathématiques, U.F.R. des Sciences et Techniques, 6, avenue Victor Le Gorgeu, BP 809 29285 Brest Cedex, France
Get access Rights & Permissions [Opens in a new window]

Abstract

By Fourier methods, it is possible to prove central limit theorems for Riesz-Raikov sums 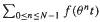for any real θ > 1 and for a quite large class of functions f.

The same problem is solved here for Hölder-continuous functions f and Pisot–Vijayaragavan numbers θ in a totally different way: it is shown that the question is equivalent to working with ergodic sums 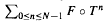for suitable functions F on [0;l], and T denoting the θ-transformation x ↦ θx mod 1. In addition, limit theorems are proved on the θ-shifts, for any real θ 1.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 16 , Issue 2 , April 1996 , pp. 335 - 364
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Be]Bertrand-Mathis, A.. Développement en base θ, répartition modulo un de la suite {xθn}, langages codes et θ-shifts. Bull. Soc. math. France. 114 (1986), 271–323.Google Scholar
[Bl]Blank, M. L.. Stochastic properties of deterministic dynamical systems. Sov. Sci. Rev. C Maths/Phys. 6 (1987), 243–271.Google Scholar
[Bo]Bowen, R.. Equilibrium states and the ergodic theory of Anosov diffeomorphisms. Lecture Notes Math. 470. Berlin, Springer, 1975.Google Scholar
[Br]Breiman, L.. Probability. Addison-Wesley, Reading, 1968.Google Scholar
[C]Cigler, J.. Ziffernverteilung in θ-adischen Brchen. Math. Z. 75 (1961), 8–13.Google Scholar
[CCC]Calderoni, P., Campanino, M. and Capocaccia, D.. A local limit theorem for a sequence of interval transformations. Ergod. Th. & Dynam. Sys. 5 (1985), 185–201.Google Scholar
[Fi]Fischer, R.. Ergodische Theorie von Ziffernentwicklungen und Wahrscheinlichkeitsráumen. Math. Z. 128 (1972), 217–230.Google Scholar
[Fu]Fukuyama, K.The central limit theorem for the Riesz-Raikov sums. Probab. Theory Related Fields. 100(1)(1994), 57–75.CrossRefGoogle Scholar
[GH]Guivarc'h, Y. and Hardy, J.. Théorèmes limites pour une clase de chaînes de Markov et applications aux difféomorphismes d'Anosov. Ann. last. H. P. 24(1) (1988), 73–98.Google Scholar
[Hk]Hofbauer, F. and Keller, G.. Ergodic properties of invariant measures for piecewise monotonic transformations. Math. Z. 180 (1982), 119–140.Google Scholar
[IM]Ionescu Tulcea, C. T. and Marinescu, G.. Théorie ergodique pour des classes d'opérateurs non completement continus. Ann. Math. 47 (1946), 140–147.Google Scholar
[IT]Ito, S. and Takahashi, Y.. Markov subshifts and realization of β-expansions. J. Math. Soc. Japan. 26(1) (1974), 33–55.Google Scholar
[Ka]Kac, M.. On the distribution of values of sums of the form Σ f(2kt). Ann. Math. 47 (1946), 33–49.Google Scholar
[Ke]Keller, G.. Generalized bounded variation and applications to piecewise monotonic transformations. Z. Wahr. verw. Geb. 69 (1985), 461–478.Google Scholar
[Pa]Parry, W.. On the β-expansions of real numbers. Acta Math. Acad. Sc. Hung. 11 (1960), 401–416.Google Scholar
[Pe]Petit, B.. Le théorème limite central pour des sommes de Riesz-Raikov. Probab. Theory Related Fields. 93 (1992), 407–438.Google Scholar
[Ph]Philipp, W.. Some metrical theorems in number theory. Pacific J. Math. 20 (1983), 599–629.Google Scholar
[Ro]Rousseau-Egele, J.. Un théorème de la limite locale pour une classe de transformations dilatantes et monotones par morceaux. Ann. Prob. 11(3) (1983), 772–788.Google Scholar
[Wo]Wong, S.. Hölder continuous derivatives and ergodic theory. J. Land. Math. Soc. 22 (1980), 506–520.CrossRefGoogle Scholar