Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T01:51:44.673Z Has data issue: false hasContentIssue false
  • English
  • Français

A transfer-operator-based relation between Laplace eigenfunctions and zeros of Selberg zeta functions

Published online by Cambridge University Press:  10 August 2018

ALEXANDER ADAM  and
ANKE POHL
ALEXANDER ADAM
Affiliation:
Institut de Mathématiques de Jussieu – Paris Rive Gauche, Sorbonne Université, Campus Pierre et Marie Curie, 4, place Jussieu, Boite Courrier 247, 75252 Paris Cedex 05, France email [email protected]
ANKE POHL
Affiliation:
University of Bremen, Department 3 – Mathematics, Bibliothekstr. 5, 28359 Bremen, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Over the last few years Pohl (partly jointly with coauthors) has developed dual ‘slow/fast’ transfer operator approaches to automorphic functions, resonances, and Selberg zeta functions for a certain class of hyperbolic surfaces 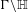$\unicode[STIX]{x1D6E4}\backslash \mathbb{H}$ with cusps and all finite-dimensional unitary representations $\unicode[STIX]{x1D712}$ of $\unicode[STIX]{x1D6E4}$. The eigenfunctions with eigenvalue 1 of the fast transfer operators determine the zeros of the Selberg zeta function for 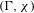$(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D712})$. Further, if $\unicode[STIX]{x1D6E4}$ is cofinite and $\unicode[STIX]{x1D712}$ is the trivial one-dimensional representation then highly regular eigenfunctions with eigenvalue 1 of the slow transfer operators characterize Maass cusp forms for $\unicode[STIX]{x1D6E4}$. Conjecturally, this characterization extends to more general automorphic functions as well as to residues at resonances. In this article we study, without relying on Selberg theory, the relation between the eigenspaces of these two types of transfer operators for any Hecke triangle surface 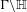$\unicode[STIX]{x1D6E4}\backslash \mathbb{H}$ of finite or infinite area and any finite-dimensional unitary representation $\unicode[STIX]{x1D712}$ of the Hecke triangle group $\unicode[STIX]{x1D6E4}$. In particular, we provide explicit isomorphisms between relevant subspaces. This solves a conjecture by Möller and Pohl, characterizes some of the zeros of the Selberg zeta functions independently of the Selberg trace formula, and supports the previously mentioned conjectures.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 3 , March 2020 , pp. 612 - 662
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman, N. and Zelditch, S.. Patterson–Sullivan distributions and quantum ergodicity. Ann. Henri Poincaré 8(2) (2007), 361–426.Google Scholar
Artin, E.. Ein mechanisches System mit quasiergodischen Bahnen. Abh. Math. Semin. Univ. Hambg. 3 (1924), 170–175.Google Scholar
Bettin, S. and Conrey, B.. Period functions and cotangent sums. Algebra Number Theory 7(1) (2013), 215–242.Google Scholar
Borthwick, D.. Distribution of resonances for hyperbolic surfaces. Exp. Math. 23(1) (2014), 25–45.Google Scholar
Borthwick, D. and Weich, T.. Symmetry reduction of holomorphic iterated function schemes and factorization of Selberg zeta functions. J. Spectr. Theory 6(2) (2016), 267–329.Google Scholar
Bourgain, J., Gamburd, A. and Sarnak, P.. Generalization of Selberg’s 3/16 theorem and affine sieve. Acta Math. 207(2) (2011), 255–290.Google Scholar
Bourgain, J. and Kontorovich, A.. On Zaremba’s conjecture. Ann. of Math. (2) 180(2) (2014), 1–60.Google Scholar
Bruggeman, R.. Automorphic forms, hyperfunction cohomology, and period functions. J. Reine Angew. Math. 492 (1997), 1–39.Google Scholar
Bruggeman, R., Fraczek, M. and Mayer, D.. Perturbation of zeros of the Selberg zeta function for 𝛤0(4). Exp. Math. 22(3) (2013), 217–242.Google Scholar
Bruggeman, R., Lewis, J. and Zagier, D.. Period functions for Maass wave forms and cohomology. Mem. Amer. Math. Soc. 237 (2015).Google Scholar
Bruggeman, R. and Mühlenbruch, T.. Eigenfunctions of transfer operators and cohomology. J. Number Theory 129(1) (2009), 158–181.Google Scholar
Bunke, U. and Olbrich, M.. Group cohomology and the singularities of the Selberg zeta function associated to a Kleinian group. Ann. of Math. (2) 149(2) (1999), 627–689.Google Scholar
Chang, C.-H. and Mayer, D.. The period function of the nonholomorphic Eisenstein series for PSL(2, Z). Math. Phys. Electron. J. 4 (1998), Paper 6, 8.Google Scholar
Chang, C.-H. and Mayer, D.. The transfer operator approach to Selberg’s zeta function and modular and Maass wave forms for PSL(2, Z). Emerging Applications of Number Theory (Minneapolis, MN, 1996) (IMA Volumes in Mathematics and its Applications, 109) . Springer, New York, 1999, pp. 73–141.Google Scholar
Chang, C.-H. and Mayer, D.. Eigenfunctions of the transfer operators and the period functions for modular groups. Dynamical, Spectral, and Arithmetic Zeta Functions (San Antonio, TX, 1999) (Contemporary Mathematics, 290) . American Mathematical Society, Providence, RI, 2001, pp. 1–40.Google Scholar
Chang, C.-H. and Mayer, D.. An extension of the thermodynamic formalism approach to Selberg’s zeta function for general modular groups. Ergodic Theory, Analysis, and Efficient Simulation of Dynamical Systems. Springer, Berlin, 2001, pp. 523–562.Google Scholar
Deitmar, A. and Hilgert, J.. Cohomology of arithmetic groups with infinite dimensional coefficient spaces. Doc. Math. 10 (2005), 199–216 (electronic).Google Scholar
Deitmar, A. and Hilgert, J.. A Lewis correspondence for submodular groups. Forum Math. 19(6) (2007), 1075–1099.Google Scholar
Efrat, I.. Dynamics of the continued fraction map and the spectral theory of SL(2, Z). Invent. Math. 114(1) (1993), 207–218.Google Scholar
Fraczek, M.. Character deformation of the Selberg zeta function for congruence subgroups via the transfer operator. Doctoral Thesis, Clausthal University of Technology, 2012.Google Scholar
Fraczek, M. and Mayer, D.. Symmetries of the transfer operator for 𝛤0(N) and a character deformation of the Selberg zeta function for 𝛤0(4). Algebra Number Theory 6(3) (2012), 587–610.Google Scholar
Fraczek, M., Mayer, D. and Mühlenbruch, T.. A realization of the Hecke algebra on the space of period functions for 𝛤0(n). J. Reine Angew. Math. 603 (2007), 133–163.Google Scholar
Fried, D.. The zeta functions of Ruelle and Selberg. I. Ann. Sci. Éc. Norm. Supér. (4) 19(4) (1986), 491–517.Google Scholar
Fried, D.. Symbolic dynamics for triangle groups. Invent. Math. 125(3) (1996), 487–521.Google Scholar
Guillopé, L., Lin, K. and Zworski, M.. The Selberg zeta function for convex co-compact Schottky groups. Commun. Math. Phys. 245(1) (2004), 149–176.Google Scholar
Hilgert, J., Mayer, D. and Movasati, H.. Transfer operators for 𝛤0(n) and the Hecke operators for the period functions of PSL(2, ℤ). Math. Proc. Cambridge Philos. Soc. 139(1) (2005), 81–116.Google Scholar
Hilgert, J. and Pohl, A.. Symbolic dynamics for the geodesic flow on locally symmetric orbifolds of rank one. Proceedings of the Fourth German–Japanese Symposium on Infinite Dimensional Harmonic Analysis IV. On the Interplay between Representation Theory, Random Matrices, Special Functions, and Probability (Tokyo, Japan, September 10–14, 2007). World Scientific, Hackensack, NJ, 2009, pp. 97–111.Google Scholar
Juhl, A.. Cohomological Theory of Dynamical Zeta Functions. Birkhäuser, Basel, 2001.Google Scholar
Katsurada, M.. Power series and asymptotic series associated with the Lerch zeta-function. Proc. Japan Acad. 10 (1998), 167–170.Google Scholar
Lax, P. and Phillips, R.. The asymptotic distribution of lattice points in Euclidean and non-Euclidean spaces. J. Funct. Anal. 46 (1982), 280–350.Google Scholar
Lax, P. and Phillips, R.. Translation representations for automorphic solutions of the wave equation in non-Euclidean spaces. I. Comm. Pure Appl. Math. 37 (1984), 303–328.Google Scholar
Lax, P. and Phillips, R.. Translation representations for automorphic solutions of the wave equation in non-Euclidean spaces. II. Comm. Pure Appl. Math. 37 (1984), 779–813.Google Scholar
Lax, P. and Phillips, R.. Translation representations for automorphic solutions of the wave equation in non-Euclidean spaces. III. Comm. Pure Appl. Math. 38 (1985), 179–207.Google Scholar
Lewis, J. and Zagier, D.. Period functions for Maass wave forms. I. Ann. of Math. (2) 153(1) (2001), 191–258.Google Scholar
Mayer, D.. On the thermodynamic formalism for the Gauss map. Comm. Math. Phys. 130(2) (1990), 311–333.Google Scholar
Mayer, D.. The thermodynamic formalism approach to Selberg’s zeta function for PSL(2, Z). Bull. Amer. Math. Soc. (N.S.) 25(1) (1991), 55–60.Google Scholar
Mayer, D., Mühlenbruch, T. and Strömberg, F.. The transfer operator for the Hecke triangle groups. Discrete Contin. Dyn. Syst. 32(7) (2012), 2453–2484.Google Scholar
Mayer, D. and Strömberg, F.. Symbolic dynamics for the geodesic flow on Hecke surfaces. J. Mod. Dyn. 2(4) (2008), 581–627.Google Scholar
Möller, M. and Pohl, A.. Period functions for Hecke triangle groups, and the Selberg zeta function as a Fredholm determinant. Ergod. Th. & Dynam. Sys. 33(1) (2013), 247–283.Google Scholar
Morita, T.. Markov systems and transfer operators associated with cofinite Fuchsian groups. Ergod. Th. & Dynam. Sys. 17(5) (1997), 1147–1181.Google Scholar
Naud, F.. Expanding maps on Cantor sets and analytic continuation of zeta functions. Ann. Sci. Éc. Norm. Supér. (4) 38(1) (2005), 116–153.Google Scholar
Patterson, S.. The limit set of a Fuchsian group. Acta Math. 136 (1976), 241–273.Google Scholar
Patterson, S.. On Ruelle’s zeta-function. Festschrift in Honor of I. I. Piatetski-Shapiro on the Occasion of his Sixtieth Birthday. Pt. II: Papers in Analysis, Number Theory and Automorphic L-functions (Tel-Aviv, Israel 1989) (Israel Mathematics Conf. Proc., 3) . Weizmann, Jerusalem, 1990, pp. 163–184.Google Scholar
Patterson, S. and Perry, P.. The divisor of Selberg’s zeta function for Kleinian groups. Appendix A by Charles Epstein. Duke Math. J. 106(2) (2001), 321–390.Google Scholar
Pohl, A.. Symbolic dynamics for the geodesic flow on locally symmetric good orbifolds of rank one. Doctoral Thesis, University of Paderborn, 2009, http://d-nb.info/gnd/137984863.Google Scholar
Pohl, A.. A dynamical approach to Maass cusp forms. J. Mod. Dyn. 6(4) (2012), 563–596.Google Scholar
Pohl, A.. Period functions for Maass cusp forms for 𝛤0(p): a transfer operator approach. Int. Math. Res. Not. IMRN 14 (2013), 3250–3273.Google Scholar
Pohl, A.. Symbolic dynamics for the geodesic flow on two-dimensional hyperbolic good orbifolds. Discrete Contin. Dyn. Syst. 34(5) (2014), 2173–2241.Google Scholar
Pohl, A.. A thermodynamic formalism approach to the Selberg zeta function for Hecke triangle surfaces of infinite area. Comm. Math. Phys. 337(1) (2015), 103–126.Google Scholar
Pohl, A.. Odd and even Maass cusp forms for Hecke triangle groups, and the billiard flow. Ergod. Th. & Dynam. Sys. 36(1) (2016), 142–172.Google Scholar
Pohl, A.. Symbolic dynamics, automorphic functions, and Selberg zeta functions with unitary representations. Dynamics and Numbers (Contemp. Math., 669) . Eds. Kolyada, S., Möller, M., Moree, P. and Ward, T.. American Mathematical Society, Providence, RI, 2016, pp. 205–236.Google Scholar
Pohl, A. and Spratte, V.. A geometric reduction theory for indefinite binary quadratic forms over $\mathbb{Z}[\unicode[STIX]{x1D706}]$ . Preprint, 2015, arXiv:1512.08090.Google Scholar
Pollicott, M.. Some applications of thermodynamic formalism to manifolds with constant negative curvature. Adv. Math. 85 (1991), 161–192.Google Scholar
Raghunathan, M. S.. Discrete Subgroups of Lie Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, 68) . Springer, Berlin, 1972.Google Scholar
Selberg, A.. Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series. J. Indian Math. Soc. (N.S.) 20 (1956), 47–87.Google Scholar
Series, C.. The modular surface and continued fractions. J. Lond. Math. Soc. (2) 31(1) (1985), 69–80.Google Scholar
Sullivan, D.. The density at infinity of a discrete group of hyperbolic motions. Publ. Math. Inst. Hautes Études. Sci. 50 (1979), 171–202.Google Scholar
Venkov, A. B.. Spectral theory of automorphic functions. Proc. Steklov Inst. Math. 153(4) (1982), 1–163; transl. of Trudy Mat. Inst. Steklov. 153 (1981), 3–171.Google Scholar