Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:37:11.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Topologically completely positive entropy and zero-dimensional topologically completely positive entropy

Published online by Cambridge University Press:  14 March 2017

RONNIE PAVLOV
RONNIE PAVLOV*
Affiliation:
Department of Mathematics, University of Denver, 2280 S. Vine Street, Denver, CO 80208, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In a previous paper [Pavlov, A characterization of topologically completely positive entropy for shifts of finite type. Ergod. Th. & Dynam. Sys.34 (2014), 2054–2065], the author gave a characterization for when a 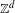$\mathbb{Z}^{d}$-shift of finite type has no non-trivial subshift factors with zero entropy, a property which we here call zero-dimensional topologically completely positive entropy. In this work, we study the difference between this notion and the more classical topologically completely positive entropy of Blanchard. We show that there are one-dimensional subshifts and two-dimensional shifts of finite type which have zero-dimensional topologically completely positive entropy but not topologically completely positive entropy. In addition, we show that strengthening the hypotheses of the main result of Pavlov [A characterization of topologically completely positive entropy for shifts of finite type. Ergod. Th. & Dynam. Sys.34 (2014), 2054–2065] yields a sufficient condition for a 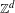$\mathbb{Z}^{d}$-shift of finite type to have topologically completely positive entropy.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 5 , August 2018 , pp. 1894 - 1922
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blanchard, F.. Fully positive topological entropy and topological mixing. Symbolic Dynamics and its Applications (New Haven, CT, 1991) (Contemporary Mathematics, 135) . American Mathematical Society, Providence, RI, 1992, pp. 95–105.Google Scholar
Blanchard, F. and Kürka, P.. Language complexity of rotations and Sturmian sequences. Theoret. Comput. Sci. 209(1–2) (1998), 179–193.CrossRefGoogle Scholar
Bowen, R.. Periodic points and measures for Axiom A diffeomorphisms. Trans. Amer. Math. Soc. 154 (1971), 377–397.Google Scholar
Boyle, M., Pavlov, R. and Schraudner, M.. Multidimensional sofic shifts without separation and their factors. Trans. Amer. Math. Soc. 362(9) (2010), 4617–4653.CrossRefGoogle Scholar
Hochman, M.. On the automorphism groups of multidimensional shifts of finite type. Ergod. Th. & Dynam. Sys. 30(3) (2010), 809–840.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Lothaire, M.. Algebraic Combinatorics on Words (Encyclopedia of Mathematics and its Applications, 90) . Cambridge University Press, Cambridge, 2002.Google Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.Google Scholar
Pavlov, R.. A characterization of topologically completely positive entropy for shifts of finite type. Ergod. Th. & Dynam. Sys. 34(6) (2014), 2054–2065.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, Berlin, 1975.Google Scholar