Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T01:08:19.738Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological enumeration of complex polynomial vector fields

Published online by Cambridge University Press:  10 January 2014

J. TOMASINI
J. TOMASINI*
Affiliation:
Laboratoire Angevin de REcherche en MAthématiques (LAREMA), Université d’Angers, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The enumeration of combinatorial classes of the complex polynomial vector fields in 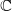$ \mathbb{C} $ presented by K. Dias [Enumerating combinatorial classes of the complex polynomial vector fields in $ \mathbb{C} $. Ergod. Th. & Dynam. Sys. 33 (2013), 416–440] is extended here to a closed form enumeration of combinatorial classes for degree 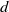$d$ polynomial vector fields up to rotations of the $2(d- 1)\mathrm{th} $ roots of unity. The main tool in the proof of this result is based on a general method of enumeration developed by V. A. Liskovets [Reductive enumeration under mutually orthogonal group actions. Acta Appl. Math. 52 (1998), 91–120].

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 4 , June 2015 , pp. 1315 - 1344
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alverez, M. J., Gasull, A. and Prohens, R.. Topological classification of polynomial complex differential equations with all the critical points of centre type. J. Difference Equ. Appl. 16 (2010), 411–423.CrossRefGoogle Scholar
Branner, B. and Dias, K.. Classification of complex polynomial vector fields in one complex variable. J. Difference Equ. Appl. 16 (2010), 463–517.CrossRefGoogle Scholar
Benchekroun, S. and Moszkowski, P.. A new bijection between ordered trees and legal bracketings. European J. Combin. 17 (1996), 605–611.CrossRefGoogle Scholar
Davis, T.. Catalan numbers, 2012, http://geometer.org/mathcircles/catalan.pdf.Google Scholar
Dias, K.. Enumerating combinatorial classes of the complex polynomial vector fields in $ \mathbb{C} $. Ergod. Th. & Dynam. Sys. 33 (2013), 416–440.CrossRefGoogle Scholar
Douady, A., Estrada, F. and Sentenac, P.. Champs de vecteurs polynômiaux sur $ \mathbb{C} $, unpublished manuscript.Google Scholar
Liskovets, V. A.. A reductive technique for enumerating non-isomorphic planar maps. Discrete Math. 156 (1996), 197–217.CrossRefGoogle Scholar
Liskovets, V. A.. Reductive enumeration under mutually orthogonal group actions. Acta Appl. Math. 52 (1998), 91–120.CrossRefGoogle Scholar
Liskovets, V. A.. Enumerative formulae for unrooted planar maps: a pattern. Electron. J. Combin. 11 (2004).CrossRefGoogle Scholar
Mani, P.. Automorphismen von polyedrischen graphen. Math. Ann. 192 (1971), 279–303.CrossRefGoogle Scholar
Pilgrim, K. M.. Polynomial vector fields, dessins d’enfants, and circle packings. Complex Dynamics (Contemporary Mathematics, 396). American Mathematical Society, Providence, RI, 2006.Google Scholar