Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T01:12:42.107Z Has data issue: false hasContentIssue false
  • English
  • Français

The topological entropy of non-dense orbits and generalized Schmidt games

Published online by Cambridge University Press:  18 May 2017

WEISHENG WU
WEISHENG WU*
Affiliation:
Department of Applied Mathematics, College of Science, China Agricultural University, Beijing 100083, PR China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize the notion of Schmidt games to the setting of the general Caratheódory construction. The winning sets for such generalized Schmidt games usually have large corresponding Caratheódory dimensions (e.g., Hausdorff dimension and topological entropy). As an application, we show that for every 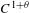$C^{1+\unicode[STIX]{x1D703}}$-partially hyperbolic diffeomorphism 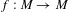$f:M\rightarrow M$ satisfying certain technical conditions, the topological entropy of the set of points with non-dense forward orbits is bounded below by the unstable metric entropy (in the sense of Ledrappier–Young) of certain invariant measures. This also gives a unified proof of the fact that the topological entropy of such a set is equal to the topological entropy of 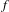$f$, when 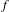$f$ is a toral automorphism or the time-one map of a certain non-quasiunipotent homogeneous flow.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 2 , February 2019 , pp. 500 - 530
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abercrombie, A. G. and Nair, R.. An exceptional set in the ergodic theory of expanding maps on manifolds. Monatsh. Math. 148(1) (2006), 1–17.Google Scholar
Adler, R. L., Konheim, A. G. and McAndrew, M. H.. Topological entropy. Trans. Amer. Math. Soc. 114(2) (1965), 309–319.Google Scholar
An, J.. Two dimensional badly approximable vectors and Schmidt’s game. Duke Math. J. 165(2) (2016), 267–284.Google Scholar
An, J., Guan, L. and Kleinbock, D.. Bounded orbits of diagonalizable flows on SL3(ℝ)/SL3(ℤ). Int. Math. Res. Not. IMRN 24 (2015), 13623–13652.Google Scholar
Aravinda, C. S. and Leuzinger, E.. Bounded geodesics in rank-1 locally symmetric spaces. Ergod. Th. & Dynam. Sys. 15(5) (1995), 813–820.Google Scholar
Bergelson, V., Einsiedler, M. and Tseng, J.. Simultaneous dense and nondense orbits for commuting maps. Israel J. Math. 210 (2015), 23–45.Google Scholar
Bowen, R.. Topological entropy for noncompact sets. Trans. Amer. Math. Soc. 184 (1973), 125–136.Google Scholar
Broderick, R., Fishman, L. and Kleinbock, D. Y.. Schmidt’s game, fractals, and orbits of toral endomorphisms. Ergod. Th. & Dynam. Sys. 31 (2011), 1095–1107.Google Scholar
Broderick, R., Fishman, L. and Simmons, D.. Badly approximable systems of affine forms and incompressibility on fractals. J. Number Theory 31(4) (2011), 1095–1107.Google Scholar
Dani, S. G.. Divergent trajectories of flows on homogeneous spaces and Diophantine approximation. J. Reine Angew. Math. 359 (1985), 55–89.Google Scholar
Dani, S. G.. Bounded orbits of flows on homogeneous spaces. Comment. Math. Helv. 61(1) (1986), 636–660.Google Scholar
Dani, S. G.. On orbits of endomorphisms of tori and the Schmidt game. Ergod. Th. & Dynam. Sys. 8(04) (1988), 523–529.Google Scholar
Dani, S. G. and Shah, H.. Badly approximable numbers and vectors in Cantor-like sets. Proc. Amer. Math. Soc. 140(8) (2012), 2575–2587.Google Scholar
Dolgopyat, D.. Bounded orbits of Anosov flows. Duke Math. J. 87(1) (1997), 87–114.Google Scholar
Einsiedler, M. and Tseng, J.. Badly approximable systems of affine forms, fractals, and Schmidt games. J. Reine Angew. Math. 660 (2011), 83–97.Google Scholar
Guan, L. and Wu, W.. Bounded orbits of certain diagonalizable flows on $\text{SL}_{n}(\mathbb{R})/\text{SL}_{n}(\mathbb{Z})$ . Trans. Amer. Math. Soc., to appear.Google Scholar
Guan, L. and Yu, J.. Badly approximable vectors in higher dimension. Preprint, 2015, arXiv:1509.08050.Google Scholar
Kleinbock, D. Y.. Flows on homogeneous spaces and Diophantine properties of matrices. Duke Math. J. 95(1) (1998), 107–124.Google Scholar
Kleinbock, D. Y. and Margulis, G. A.. Bounded orbits of nonquasiunipotent flows on homogeneous spaces. Amer. Math. Soc. Trans. 171 (1996), 141–172.Google Scholar
Kleinbock, D. Y. and Weiss, B.. Modified Schmidt games and Diophantine approximation with weights. Adv. Math. 223(4) (2010), 1276–1298.Google Scholar
Kleinbock, D. Y. and Weiss, B.. Modified Schmidt games and a conjecture of Margulis. J. Mod. Dyn. 7 (2013), 429–460.Google Scholar
Ledrappier, F. and Strelcyn, J.-M.. A proof of the estimation from below in Pesin’s entropy formula. Ergod. Th. & Dynam. Sys. 2(02) (1982), 203–219.Google Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms. Part I: characterization of measures satisfying Pesin’s entropy formula. Ann. of Math. (2) 122 (1985), 509–539.Google Scholar
Ledrappier, F. and Young, L. S.. The metric entropy of diffeomorphisms. Part II: relations between entropy, exponents and dimension. Ann. of Math. (2) 122 (1985), 540–574.Google Scholar
McMullen, C.. Area and Hausdorff dimension of Julia sets of entire functions. Trans. Amer. Math. Soc. 300(1) (1987), 329–342.Google Scholar
Pesin, Y. B.. Dimension Theory in Dynamical Systems: Contemporary Views and Applications (Chicago Lectures in Mathematics) . University of Chicago Press, Chicago, 2008.Google Scholar
Pesin, Y. B. and Pitskel′, B. S.. Topological pressure and the variational principle for noncompact sets. Funct. Anal. Appl. 18(4) (1984), 307–318.Google Scholar
Pesin, Ya. B. and Sinai, Ya. G.. Gibbs measures for partially hyperbolic attractors. Ergod. Th. & Dynam. Sys. 2(3–4) (1982), 417–438.Google Scholar
Rodriguez, F., Hertz, M. A., Hertz, R. and Ures, R.. Accessibility and stable ergodicity for partially hyperbolic diffeomorphisms with 1d-center bundle. Invent. Math. 172(2) (2008), 353–381.Google Scholar
Rohlin, V. A.. On the fundamental ideas of measure theory. Amer. Math. Soc. Trans. 71 (1952), 55 pp. Engl. Transl. of Mat. Sbornik 25 (1949), 107–150.Google Scholar
Schmidt, W. M.. On badly approximable numbers and certain games. Trans. Amer. Math. Soc. 123(1) (1966), 178–199.Google Scholar
Schmidt, W. M.. Badly approximable systems of linear forms. J. Number Theory 1(2) (1969), 139–154.Google Scholar
Tang, X., Cheng, W. C. and Zhao, Y.. Variational principle for topological pressures on subsets. J. Math. Anal. Appl. 424(2) (2015), 1272–1285.Google Scholar
Tseng, J.. Schmidt games and Markov partitions. Nonlinearity 22(3) (2009), 525–543.Google Scholar
Tseng, J.. Nondense orbits for Anosov diffeomorphisms of the 2-torus. Real Anal. Exchange 41(2) (2016), 307–314.Google Scholar
Urbański, M.. The Hausdorff dimension of the set of points with nondense orbit under a hyperbolic dynamical system. Nonlinearity 4(2) (1991), 385–397.Google Scholar
Wu, W.. Schmidt games and non-dense forward orbits of certain partially hyperbolic systems. Ergod. Th. & Dynam. Sys. 36(5) (2016), 1656–1678.Google Scholar
Wu, W.. Modified Schmidt games and non-dense forward orbits of partially hyperbolic systems. Discrete Contin. Dyn. Syst. Ser. A 36(6) (2016), 3463–3481.Google Scholar
Wu, W.. On non-dense orbits of certain non-algebraic dynamical systems. J. Dynam. Differential Equations, to appear.Google Scholar
Zhao, Y. and Pesin, Y.. Scaled entropy for dynamical systems. J. Stat. Phys. 158(2) (2015), 447–475.Google Scholar