Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T01:20:03.028Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological and algebraic reducibility for patterns on trees

Published online by Cambridge University Press:  13 August 2013

LLUÍS ALSEDÀ ,
DAVID JUHER  and
FRANCESC MAÑOSAS
LLUÍS ALSEDÀ
Affiliation:
Departament de Matemàtiques, Edifici Cc, Universitat Autònoma de Barcelona, 08913 Cerdanyola del Vallès, Barcelona, Spain
DAVID JUHER
Affiliation:
Departament d’Informàtica i Matemàtica Aplicada, Universitat de Girona, Lluís Santaló s/n, 17071 Girona, Spain email [email protected]
FRANCESC MAÑOSAS
Affiliation:
Departament de Matemàtiques, Edifici Cc, Universitat Autònoma de Barcelona, 08913 Cerdanyola del Vallès, Barcelona, Spain
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend the classical notion of block structure for periodic orbits of interval maps to the setting of tree maps and study the algebraic properties of the Markov matrix of a periodic tree pattern having a block structure. We also prove a formula which relates the topological entropy of a pattern having a block structure with that of the underlying periodic pattern obtained by collapsing each block to a point, and characterize the structure of the zero entropy patterns in terms of block structures. Finally, we prove that an $n$-periodic pattern has zero (positive) entropy if and only if all $n$-periodic patterns obtained by considering the 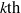$k\mathrm{th} $ iterate of the map on the invariant set have zero (respectively, positive) entropy, for each 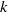$k$ relatively prime to $n$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 1 , February 2015 , pp. 34 - 63
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. L., Konheim, A. G. and McAndrew, M. H.. Topological entropy. Trans. Amer. Math. Soc. 114 (1965), 309–319.Google Scholar
Alsedà, Ll. and Ye, X.. Division for star maps with the branching point fixed. Acta Math. Univ. Comenian. (N.S.) 62 (2) (1993), 237–248.Google Scholar
Alsedà, Ll., Los, J., Mañosas, F. and Mumbrú, P.. Canonical representatives for patterns of tree maps. Topology 36 (5) (1997), 1123–1153.Google Scholar
Alsedà, Ll., Llibre, J. and Misiurewicz, M.. Combinatorial Dynamics and Entropy in Dimension One (Advanced Series in Nonlinear Dynamics, 5), 2nd edn. World Scientific, River Edge, NJ, 2000.Google Scholar
Alsedà, Ll. and Ye, X.. No division and the set of periods for tree maps. Ergod. Th. & Dynam. Sys. 15 (2) (1995), 221–237.Google Scholar
Block, L., Guckenheimer, J., Misiurewicz, M. and Young, L. S.. Periodic points and topological entropy of one-dimensional maps. Global Theory of Dynamical Systems (Springer Lecture Notes in Mathematics, 819). Springer, Berlin, 1980, pp. 18–34.Google Scholar
Block, L.. Simple periodic orbits of mappings of the interval. Trans. Amer. Math. Soc. 254 (1979), 391–398.Google Scholar
Gantmacher, F. R.. The Theory of Matrices,2nd edn. AMS Chelsea Publishing Company, New York, 1989–90.Google Scholar
Li, T. Y., Misiurewicz, M., Pianigiani, G. and Yorke, J. A.. No division implies chaos. Trans. Amer. Math. Soc. 273 (1) (1982), 191–199.Google Scholar
Llibre, J. and Misiurewicz, M.. Horseshoes, entropy and periods for graph maps. Topology 32 (3) (1993), 649–664.Google Scholar
Rudin, W.. Principles of Mathematical Analysis. McGraw-Hill, Singapore, 1976.Google Scholar
Sharkovskii, O. M.. Co-existence of cycles of a continuous mapping of the line into itself. Ukraïn. Mat. Zh. 16 (1964), 61–71.Google Scholar
Thurston, W. P.. On the geometry and dynamics of diffeomorphisms of surfaces. Bull. Amer. Math. Soc. (N.S.) 19 (2) (1988), 417–431.CrossRefGoogle Scholar