Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-19T10:57:39.308Z Has data issue: false hasContentIssue false
  • English
  • Français

The Toeplitz noncommutative solenoid and its Kubo–Martin–Schwinger states

Published online by Cambridge University Press:  03 April 2017

NATHAN BROWNLOWE ,
MITCHELL HAWKINS  and
AIDAN SIMS
NATHAN BROWNLOWE
Affiliation:
School of Mathematics and Statistics, University of Sydney, NSW 2006, Australia email [email protected]
MITCHELL HAWKINS
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, NSW 2522, Australia email [email protected], [email protected]
AIDAN SIMS
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, NSW 2522, Australia email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We use Katsura’s topological graphs to define Toeplitz extensions of Latrémolière and Packer’s noncommutative-solenoid 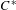$C^{\ast }$-algebras. We identify a natural dynamics on each Toeplitz noncommutative solenoid and study the associated Kubo–Martin–Schwinger (KMS) states. Our main result shows that the space of extreme points of the KMS simplex of the Toeplitz noncommutative torus at a strictly positive inverse temperature is homeomorphic to a solenoid; indeed, there is an action of the solenoid group on the Toeplitz noncommutative solenoid that induces a free and transitive action on the extreme boundary of the KMS simplex. With the exception of the degenerate case of trivial rotations, at inverse temperature zero there is a unique KMS state, and only this one factors through Latrémolière and Packer’s noncommutative solenoid.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 1 , January 2019 , pp. 105 - 131
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afsar, Z., an Huef, A. and Raeburn, I.. KMS states on C ∗ -algebras associated to local homeomorphisms. Internat. J. Math. 25 (2014), 1450066.Google Scholar
an Huef, A., Laca, M., Raeburn, I. and Sims, A.. KMS states on the C ∗ -algebras of finite graphs. J. Math. Anal. Appl. 405 (2013), 388–399.Google Scholar
an Huef, A., Laca, M., Raeburn, I. and Sims, A.. KMS states on the C ∗ -algebra of a higher-rank graph and periodicity in the path space. J. Funct. Anal. 268 (2015), 1840–1875.Google Scholar
Bost, J.-B. and Connes, A.. Hecke algebras, type III factors and phase transitions with spontaneous symmetry breaking in number theory. Selecta Math. (N.S.) 1 (1995), 411–457.Google Scholar
Bratteli, O. and Robinson, D. W.. Operator Algebras and Quantum Statistical Mechanics 2: Equilibrium States Models in Quantum Statistical Mechanics. Springer, Berlin, 1997.Google Scholar
Brownlowe, N., an Huef, A., Laca, M. and Raeburn, I.. Boundary quotients of the Toeplitz algebra of the affine semigroup over the natural numbers. Ergod. Th. & Dynam. Sys. 32 (2012), 35–62.Google Scholar
Christensen, J. and Thomsen, K.. Finite digraphs and KMS states. J. Math. Anal. Appl. 433 (2016), 1626–1646.Google Scholar
Clarke, L. O., an Huef, A. and Raeburn, I.. Phase transitions on the Toeplitz algebras of Baumslag–Solitar semigroups. Indiana Univ. Math. J. 65 (2016), 2137–2173.Google Scholar
Davidson, K. R.. C ∗ -Algebras by Example. American Mathematical Society, Providence, RI, 1996.Google Scholar
Enomoto, M., Fujii, M. and Watatani, Y.. KMS states for gauge action on O A . Math. Japon. 29 (1984), 607–619.Google Scholar
Farsi, C., Gillaspy, E., Kang, S. and Packer, J. A.. Separable representations, KMS states, and wavelets for higher-rank graphs. J. Math. Anal. Appl. 434 (2016), 241–270.Google Scholar
Fowler, N. J. and Raeburn, I.. The Toeplitz algebra of a Hilbert bimodule. Indiana Univ. Math. J. 48 (1999), 155–181.Google Scholar
Hawkins, M.. Applications of compact topological graph $C^{\ast }$ -algebras to noncommutative solenoids, PhD Thesis, University of Wollongong, 2015.Google Scholar
Kajiwara, T. and Watatani, Y.. KMS states on finite-graph C ∗ -algebras. Kyushu J. Math. 67 (2013), 83–104.Google Scholar
Kakariadis, E. T. A.. KMS states on Pimsner algebras associated with C ∗ -dynamical systems. J. Funct. Anal. 269 (2015), 325–354.Google Scholar
Katsura, T.. A class of C ∗ -algebras generalizing both graph algebras and homeomorphism C ∗ -algebras I. Fundamental results. Trans. Amer. Math. Soc. 356 (2004), 4287–4322.Google Scholar
Katsura, T.. On C ∗ -algebras associated with C ∗ -correspondences. J. Funct. Anal. 217 (2004), 366–401.Google Scholar
Katsura, T.. A class of C ∗ -algebras generalizing both graph algebras and homeomorphism C ∗ -algebras II. Examples. Internat. J. Math. 17 (2006), 791–833.Google Scholar
Laca, M. and Neshveyev, S.. KMS states of quasi-free dynamics on Pimsner algebras. J. Funct. Anal. 211 (2004), 457–482.Google Scholar
Laca, M. and Raeburn, I.. Phase transition on the Toeplitz algebra of the affine semigroup over the natural numbers. Adv. Math. 225 (2010), 643–688.Google Scholar
Laca, M., Raeburn, I., Ramagge, J. and Whittaker, M. F.. Equilibrium states on the Cuntz–Pimsner algebras of self-similar actions. J. Funct. Anal. 266 (2014), 6619–6661.Google Scholar
Latrémolière, F. and Packer, J. A.. Noncommutative solenoids. New York J. Math. to appear. Preprint, 2011, arXiv:1110.6227 [math.OA].Google Scholar
Latrémolière, F. and Packer, J. A.. Commutative and noncommutative harmonic analysis and applications. Noncommutative Solenoids and Their Projective Modules (Contemporary Mathematics, 603) . American Mathematical Society, Providence, RI, 2013, pp. 35–53.Google Scholar
Latrémolière, F. and Packer, J. A.. Trends in harmonic analysis and its applications. Explicit Construction of Equivalence Bimodules between Noncommutative Solenoids (Contemporary Mathematics, 650) . American Mathematical Society, Providence, RI, 2015, pp. 111–140.Google Scholar
Phelps, R. R.. Lectures on Choquet’s Theorem. Springer, Berlin, 2001.Google Scholar
Pimsner, M. V.. A class of C ∗ -algebras generalizing both Cuntz–Krieger algebras and crossed products by Z . Free Probability Theory (Fields Institute Communications, 12) . Ed. Voiculescu, D.-V.. American Mathematical Society, Providence, RI, 1997, pp. 189–212.Google Scholar
Rudin, W.. Real and Complex Analysis. McGraw-Hill, New York, 1987.Google Scholar
Takesaki, M. and Winnink, M.. Local normality in quantum statistical mechanics. Commun. Math. Phys. 30 (1973), 129–152.Google Scholar
Yang, D.. Endomorphisms and modular theory of 2-graph C ∗ -algebras. Indiana Univ. Math. J. 59 (2010), 495–520.Google Scholar